Nội dung bài viết

    Xem thêm

    Công thức tính công sai của cấp số cộng và cách giải các dạng bài tập (2024) chi tiết nhất

    Với Công thức tính công sai của cấp số cộng Toán lớp 11 chi tiết nhất giúp học sinh dễ dàng nhớ toàn bộ các công thức về giá trị tuyệt đối của một số hữu tỉ từ đó biết cách làm bài tập Toán 11. Mời các bạn đón xem:

    1 119,907 26/08/2024
    Tải về
    Trang trước
    Chia sẻ
    Trang sau  

    Công thức tính công sai của cấp số cộng

    I. Lý thuyết về công sai cấp số cộng

    1. Cấp số cộng là gì?

    Định nghĩa: (un) là cấp số cộng khi un+1=un+d, n∈ℕ* (d gọi là công sai)

    2. Công sai là gì?

    Công sai d của cấp số cộng là số không phụ thuộc vào n.

    3. Tính chất của cấp số cộng

    Trong một cấp số cộng, mỗi số hạng (trừ số hạng đầu và cuối) đều là trung bình cộng của hai số hạng đứng kề với nó.

    Uk = uk-1+uk+12 với k ≥2

    4. Công thức tính số hạng tổng quát

    Công thức tính công sai của cấp số cộng và cách giải các dạng bài tập (2024) chi tiết nhất (ảnh 1)

    5. Công thức tổng cấp số cộng

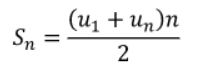
    Công thức tính công sai của cấp số cộng và cách giải các dạng bài tập (2024) chi tiết nhất (ảnh 1)

    II. Công thức tính công sai của cấp số cộng

    - Tính công sai dựa vào định nghĩa: d = un+1 – un hoặc d = u2 – u1 = u3 – u2 = …

    - Đề bài cho các dữ kiện khác: Lập hệ phương trình hai ẩn u1 và d. Tìm u1 và d.

    Ví dụ 1:

    a) Cho cấp số cộng (un) thỏa mãn: un+1 = un + 5. Tìm công sai của cấp số cộng.

    b) Cho cấp số cộng (un) thỏa mãn: un+1 = – 3n + 5. Tìm công sai của cấp số cộng.

    Lời giải

    a) Công sai của cấp số cộng là: d = un+1 – un = 5.

    b) Cách 1: Ta có: un = – 3(n – 1) + 5 = – 3n + 8

    Công sai của cấp số cộng là: d = un+1 – un = (– 3n + 5) – (–3n + 8) = – 3.

    Cách 2: Tính u1 = – 3.0 + 5 = 5 và u2 = – 3.1 + 5 = 2

    Khi đó công sai của cấp số cộng: d = u2 – u1 = 2 – 5 = – 3.

    Ví dụ 2:

    a) Cho cấp số cộng (u­n) có u4 = – 12 và u14 = 18. Tìm u1, d của cấp số cộng?

    b) Cho cấp số cộng (un) thỏa mãn: u5+3u3−u2=−213u7−2u4=−34.

    Tìm công sai của cấp số cộng.

    Lời giải

    a) Gọi d là công sai của cấp số cộng, ta có:

    u4=−12u14=18⇔u1+3d=−12u1+13d=18⇔u1=−21d=3

    Vậy u1 = – 21 và d = 3.

    b) Gọi d là công sai của cấp số cộng, ta có:

    u5+3u3−u2=−213u7−2u4=−34⇔u1+4d+3u1+2d−u1+d=−213u1+6d−2u1+3d=−34⇔3u1+9d=−21u1+12d=−34⇔u1=2d=−3

    Vậy u1 = 2 và d = – 3.

    III. Bài tập vận dụng

    Câu 1: Cho cấp số cộng u ( n ) có u1 = 5, d = 4 . Hãy tính u ( 26 )

    Ta có :

    u (26) = u1 + (26 - 1) d

    = 5 + (26 - 1) x 4

    = 105

    Câu 2: Cho cấp số cộng u ( n ) có u1 = -2, d = 7. Tìm công thức có số hạng tổng quát

    u (n) = u1 + (n - 1) d

    = -2 + (n - 1) x 7

    = 7n - 9

    Câu 3: Cho cấp số cộng u ( n ) có u1 = 1 và tổng 100 số hạng đầu bằng 24850. Tính công sai d

    Ta có S (100) = 24850

    ⇔ n / 2.( u1 + u (n)) = 24850

    ⇔ u (100) = 496

    Có u (100) = u1 + 99 d

    ⇔ d = (u (100) - u1) / 99

    ⇔ d = 5

    Xem thêm tổng hợp công thức môn Toán đầy đủ và chi tiết khác:

    Công thức tìm số hạng tổng quát của cấp số cộng

    Công thức tính tổng n số hạng đầu của cấp số cộng

    Công thức cấp số nhân

    Công thức tính công bội của cấp số nhân

    Công thức số hạng tổng quát của cấp số nhân

    Tham khảo các loạt bài Toán 11 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 119,907 26/08/2024
    Tải về
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: