Nội dung bài viết

    Xem thêm

    Công thức phép quay đầy đủ, chi tiết nhất - Toán lớp 11

    Với Công thức phép quay Toán lớp 11 chi tiết nhất giúp học sinh dễ dàng nhớ toàn bộ các công thức về giá trị tuyệt đối của một số hữu tỉ từ đó biết cách làm bài tập Toán 11. Mời các bạn đón xem:

    1 7,507 23/06/2022
    Tải về
    Trang trước
    Chia sẻ
    Trang sau  

    Công thức phép quay - Toán lớp 11

    1. Lý thuyết

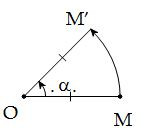
    * Định nghĩa: Cho điểm O và góc lượng giác α. Phép biến hình biến điểm O thành chính nó, biến mỗi điểm M khác O thành điểm M’ sao cho OM’ = OM và góc lượng giác (OM; OM’) bằng α được gọi là phép quay tâm O góc α.

    Điểm O được gọi là tâm quay, còn α được gọi là góc quay của phép quay đó.

    Phép quay tâm O góc α biến điểm M thành M’ thường được kí hiệu là QO, α.

    QO, αM=M'⇔OM=OM'OM,OM'=α.

    Công thức phép quay đầy đủ, chi tiết nhất - Toán lớp 11 (ảnh 1)

    * Tính chất:

    - Phép quay bảo toàn khoảng cách giữa hai điểm.

    - Biến đường thẳng thành đường thẳng.

    - Biến đoạn thẳng thành đoạn thẳng bằng nó.

    - Biến tam giác thành tam giác bằng nó.

    - Biến đường tròn thành đường tròn có cùng bán kính.

    2. Công thức

    Phép quay tâm O, góc 900: QO;90°Mx;y=M'x';y'. Khi đó: x'=−yy'=x

    Phép quay tâm O, góc -900: QO;−90°Mx;y=M'x';y'. Khi đó: x'=yy'=−x

    Phép quay tâm O, góc 1800: QO;180°Mx;y=M'x';y'. Khi đó: x'=−yy'=−x

    Tổng quát: 

    Phép quay tâm O, góc quay α: QO;αMx;y=M'x';y'.

    Khi đó: x'=xcosα−ysinαy'=xsinα+ycosα

    Phép quay tâm I(a;b), góc quay α: QI;αMx;y=M'x';y'.

    Khi đó: x'=a+x−acosα−y−bsinαy'=b+x−asinα+y+bcosα

    3. Ví dụ minh họa

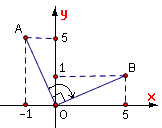
    Ví dụ 1: Trong mặt phẳng tọa độ Oxy cho điểm A(-1;5).

    a) Tìm tọa độ điểm B là ảnh của điểm A qua phép quay tâm O(0; 0) góc quay –900.

    b) Tìm tọa độ điểm C là ảnh của điểm A qua phép quay tâm O(0; 0) góc quay 450.

    Lời giải

    a) Điểm B là ảnh của điểm A qua phép quay Q(O,-90o)

    Cách 1: Vẽ hình

    Dựa vào vẽ, ta suy ra B(5;1).

    Công thức phép quay đầy đủ, chi tiết nhất - Toán lớp 11 (ảnh 1)

    Cách 2: Áp dụng công thức:

    Do Q(O,-90o)(A) = B nên xB=yA=5yB=−xA=1. Vậy B(5;1).

    b) Điểm C là ảnh của điểm A qua phép quay Q(O,45o)

    Áp dụng công thức tọa độ: xc=xAcosα−yAsinαyc=xAsinα+yAcosα

    ⇔xc=−1cos45°−5sin45°yc=−1sin45°+5cos45°

    ⇔xc=−32yc=22

    Vậy C−32;22

    Ví dụ 2: Trong mặt phẳng tọa độ Oxy cho đường thẳng d: 5x – 3y + 15 = 0.

    Tìm đường thẳng d’ là ảnh của d qua phép quay tâm O(0;0) góc quay –900.

    Lời giải

    Đường thẳng d’ là ảnh của d qua phép quay Q(O,-90o)

    Cách 1:

    Do Q(O,-90o)(d) = d’ nên d'⊥d. Do đó phương trình d’ có dạng: 3x + 5y + c = 0.

    Lấy điểm M−3;0∈d, gọi M'x'; y'∈d' là ảnh của điểm M qua phép quay Q(O,-90o)

    Suy ra: x'=yM=0y'=−xM=3⇒M'0;3.

    Do M'0;3∈d' nên 3.0 + 5.3 + c = 0⇒c=−15

    Vậy d’ có phương trình là 3x + 5y – 15 = 0.         

    Cách 2:

    Với mọi điểm Mx; y∈d,  M'x'; y'∈d' sao cho Q(O,-90o)(M) = M’.

    Khi đó ta có: x'=yy'=−x⇔x=−y'y=x'.

    Do Mx; y∈d nên ta có 5x – 3y + 15 = 0

    ⇔5−y'–3x'+15=0⇔3x’+5y’–15=0

    Do M'x'; y'∈d' nên d' có phương trình: 3x + 5y – 15 = 0.

    4. Bài tập tự luyện

    Câu 1. Trong mặt phẳng Oxy, cho điểm M(1;-5). Tìm ảnh của M qua phép quay tâm O, góc quay 900

    A. N(5;1)

    B. N(5;-1)

    C. N(1;5)

    D. N(1;-5)

    Câu 2. Trong mặt phẳng Oxy, cho đường thẳng d: 5x – 2y + 3 = 0. Viết phương trình đường thẳng d’ là ảnh của đường thẳng d qua phép quay tâm O, góc quay -1800

    A. d’: 5x – 2y + 6 = 0

    B. d’: 5x – 2y – 3 = 0        

    C. d’: 2x – 5y – 3 = 0

    D. d’: 2x – 5y + 6 = 0

    Câu 3. Trong mặt phẳng Oxy, cho đường tròn (C): x2 + y2 + 6x + 5 = 0. Ảnh của đường tròn (C) qua phép quay tâm O, góc quay 900 là:

    A. x2 + (y – 3)2 = 4

    B. x2 + y2 + 6x – 6 = 0

    C. x2 + (y + 3)2 = 4

    D. x2 + y2 + 6x – 5 = 0

    Đáp án: 1A, 2B, 3C

    Xem thêm tổng hợp công thức môn Toán lớp 9 đầy đủ và chi tiết khác:

    Công thức phép vị tự

    Công thức phép đồng dạng

    Công thức Giao tuyến của ba mặt phẳng và hệ quả

    Công thức Chứng minh hai đường thẳng song song trong không gian

    Công thức Chứng minh đường thẳng song song với mặt phẳng

    Tham khảo các loạt bài Toán 11 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 7,507 23/06/2022
    Tải về
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: