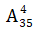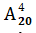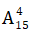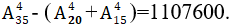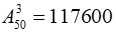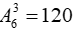Công thức chỉnh hợp (2024) đầy đủ, chi tiết nhất

Công thức chỉnh hợp chi tiết nhất

1. Lý thuyết chỉnh hợp

- Cho tập hợp A có n phần tử và cho số nguyên k, ($1\le k\le n$). Khi lấy k phần tử của A và sắp xếp chúng theo một thứ tự, ta được một chỉnh hợp chập k của n phần tử của A (gọi tắt là một chỉnh hợp n chập k của A).

- Số các chỉnh hợp chập k của một tập hợp có n phần tử là: $A_n^k=\frac{n!}{(n-k)!}$.

- Một số quy ước: $0!=1,\text{\hspace{0.17em}\hspace{0.17em}}{A}_n^0=1,A_n^n=n!$

- Đặc điểm: Đây là sắp xếp có thứ tự và số phần tử được sắp xếp là k: $0\le k\le n$.

2. Công thức tính chỉnh hợp

Công thức chỉnh hợp: $A_n^k=\frac{n!}{(n-k)!}$

3. Ví dụ minh họa

Ví dụ 1: Một đôi bóng có 11 cầu thủ, chuẩn bị đá penalty. Huấn luận viên muốn chọn ra 5 cầu thủ lần lượt lên đá penalty. Biết cả 11 cầu thủ đều có khả năng đá như nhau. Hỏi có bao nhiêu cách chọn cầu thủ lên đá bóng.

Lời giải

Số cách chọn và sắp xếp 5 cầu thủ lần lượt lên đá penalty là $A_{11}^5=55440$cách.

Ví dụ 2: Từ các chữ số từ 0 đến 9. Có bao nhiêu cách lập một số tự nhiên sao cho:

a) Số có 6 chữ số khác nhau

b) Số có 6 chữ số khác nhau và chia hết cho 10

c) Số lẻ có 6 chữ số khác nhau

Lời giải

a) Lập số có 6 chữ số khác nhau

Chọn chữ số đầu tiên từ các số từ 1 đến 9: có 9 cách chọn

Các chữ số còn lại là chỉnh hợp chập 5 của 9 số còn lại (khác chữ số đầu tiên) có $A_9^5$

Vậy có $9A_9^5=136080$ số.

b) Số có 6 chữ số khác nhau và chia hết cho 10

Chọn chữ số hàng đơn vị: có 1 cách chọn là chữ số 0

Chọn các chữ số còn lại là chỉnh hợp chập 5 của 9 số còn lại (khác chữ số 0) có $A_9^5$

Vậy có $A_9^5=15120$ số.

c) Gọi số $\overline{abcdef}$ là số lẻ có 6 chữ số khác nhau được lập từ chữ số 0 đến 9

Vì $\overline{abcdef}$ là số lẻ nên $f\in \left\{1;3;5;7;9\right\}$

Chọn f: có 5 cách chọn

Chọn a từ các chữ số {1; 2; 3; 4; 5; 6; 7; 8; 9}\{f}: có 8 cách chọn

Chọn b, c, d, e là chỉnh hợp chập 4 của 8 chữ số còn lại (khác f và a): có $A_8^4$

Vậy có $5.8A_8^4=67200$ số.

4. Bài tập vận dụng

Bài 1: Trong một lớp học có 20 học sinh nữ và 15 học sinh nam. Hỏi giáo viên chủ nhiệm có bao nhiêu cách chọn bốn học sinh làm tổ trưởng của 4 tổ sao cho trong 4 học sinh được chọn có cả nam và nữ.

A.11076 B.110760 C.1107600 D.tất cả sai

Hướng dẫn giải :

Đáp án : C

Số cách chọn 4 học sinh bất kì làm 4 tổ trưởng là :

Số cách chọn 4 học sinh làm tổ trưởng trong đó không có học sinh nam được chọn là :

Số cách chọn 4 học sinh làm tổ trưởng trong đó không có học sinh nữ được chọn là :

Vậy số cách chọn thỏa yêu cầu bài toán:

Bài 2: Một lớp có 50 học sinh. Hỏi có bao nhiêu cách phân công 3 học sinh để làm vệ sinh lớp học trong một ngày?

A.117600 B.128500 C.37600 D.24360

Hướng dẫn giải :

Đáp án : A

Số cách phân công 3 học sinh để làm vệ sinh lớp học là một chỉnh hợp của chập 3 của tập hợp có 50 học sinh. Nên số cách phân công là:

Bài 3: Có 3 tem thư khác nhau và 6 bì thư khác nhau. Người ta muốn chọn từ đó ra 3 tem thư, 3 bì thư và dán 3 tem thư đó lên 3 bì thư đã chọn, mỗi bì thư chỉ dán 1 tem thư. Hỏi có bao nhiêu cách làm như vậy?

A.200 B.30 C.300 D.120

Hướng dẫn giải :

Đáp án : D

Cố định 3 tem thư xếp theo hàng ngang từ trái sang phải là các vị trí 1, 2, 3.

Rõ ràng nếu có 3 bì thư thì mỗi thứ tự xếp 3 bì thư này từ trái sáng phải cũng chính là cách dán.

Số cách làm cần tìm là:

Bài 4: Có 5 nam và 6 nữ xếp thành một hàng dọc sao cho đầu hàng và cuối hàng luôn là nam. Hỏi có bao nhiêu cách xếp?

A.3628800 B.806400 C.7257600 D.151200

Hướng dẫn giải :

Đáp án : C

+ Số cách chọn 2 bạn nam xếp ở vị trí đầu hàng và cuối hàng là:

(ở đây ta xem cách xếp 1 bạn nam A ở đầu hàng, bạn nam B ở cuối hàng với cách xếp bạn nam A ở cuối hàng, bạn nam B ở đầu hàng là khác nhau).

+ Lúc này, còn lại 3 bạn nam và 6 bạn nữ, số cách xếp 9 người này vào 1 hàng là: 9!.

+ Vậy số cách xếp thỏa yêu cầu đề là: 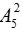.9! = 7257600 cách

Bài 5.

a. Có bao nhiêu số tự nhiên có 5 chữ số đôi một khác nhau?

b. Có bao nhiêu số tự nhiên có 5 chữ số và số đó là số chẵn?

c. Có bao nhiêu số tự nhiên có 5 chữ số đôi một khác nhau và số đó là số lẻ?

Bài 6. Có bao nhiêu số gồm 5 chữ số phân biệt có mặt đủ ba chữ số 1, 2, 3.

Bài 7. Có thể lập ra đƣợc bao nhiêu số điện thoại di động có 10 chữ số bắt đầu là 0908, các chữ số còn lại khác nhau đôi một, khác với 4 chữ số đầu và phải có mặt chữ số 6.

Bài 8. Có 6 học sinh lớp 11 và 3 học sinh lớp 12 sẽ ngồi trên một hàng ngang có 9 ghế. Hỏi có bao nhiêu cách sắp xếp chỗ ngồi cho 9 học sinh đó sao cho mỗi học sinh lớp 12 ngồi giữa hai học sinh lớp 11?

Bài 9. Xếp 5 bạn nam và 5 bạn nữ thành một hàng dọc. Hỏi có bao nhiêu cách xếp:

a) Nam nữ đứng xen kẽ.

b) Nữ luôn đứng cạnh nhau.

c) Không có 2 nam nào đứng cạnh nhau.

Xem thêm tổng hợp công thức môn Toán lớp 9 đầy đủ và chi tiết khác:

Công thức tổ hợp

Công thức khai triển nhị thức Niu-tơn

Công thức tính tổng các hệ số trong khai triển nhị thức Niu-tơn

Công thức tìm hệ số trong khai triển nhị thức Niu-tơn

Công thức tìm số hạng trong khai triển nhị thức Niu-tơn