Nội dung bài viết

    Xem thêm

    Công thức tính GTNN - GTLN của hàm số lượng giác chi tiết - Toán lớp 11

    Với Công thức tính GTNN - GTLN của hàm số lượng giác Toán lớp 11 chi tiết nhất giúp học sinh dễ dàng nhớ toàn bộ các công thức tính GTNN - GTLN của hàm số lượng giác từ đó biết cách làm bài tập Toán 11. Mời các bạn đón xem:

    1 9,929 22/06/2022
    Tải về
    Trang trước
    Chia sẻ
    Trang sau  

    Công thức tính GTNN - GTLN của hàm số lượng giác chi tiết - Toán lớp 11

    1. Lí thuyết

    a) Sử dụng tính bị chặn của hàm số lượng giác

    −1≤sinu(x)≤1; 0≤sin2u(x)≤1; 0≤sinu(x)≤1

    −1≤cosu(x)≤1; 0≤cos2u(x)≤1; 0≤cosu(x)≤1

    b) Dạng y = asinx + bcosx + c

    Bước 1: Đưa hàm số về dạng chỉ chứa sin[u(x)] hoặc cos[u(x)]:

    y = asinx + bcosx + c=a2+b2aa2+b2sinx+ba2+b2cosx+c

    ⇔y=a2+b2.sinx+α+c với α thỏa mãn

    cosα=aa2+b2;sinα=ba2+b2

    Bước 2: Đánh giá −1≤sinx+α≤1∀x∈ℝ

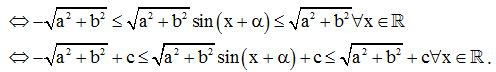
    Công thức tính GTNN - GTLN của hàm số lượng giác chi tiết - Toán lớp 11 (ảnh 1)

    2. Công thức

    a) Dạng y = asin[u(x)] + b hoặc y = acos[u(x)] + b

    Ta có: −a+b≤y≤a+b

    Hàm số có giá trị nhỏ nhất là –|a| + b và giá trị lớn nhất là |a| + b.

    b) Dạng y = asin2[u(x)] + b ; y = a|sin[u(x)]| + b;

    Dạng y = acos2[u(x)] + b; y = a|cos[u(x)]| + b (với a khác 0)

    + Trường hợp 1:  a > 0. Ta có: b≤y≤a+b.

    Hàm số có giá trị nhỏ nhất là b và giá trị lớn nhất là a + b.

    + Trường hợp 2: a < 0. Ta có: a+b≤y≤b.

    Hàm số có giá trị nhỏ nhất là a + b và giá trị lớn nhất là b.

    c) Dạng y = asinx + bcosx + c

    Ta có: −a2+b2+c≤y≤a2+b2+c

    Hàm số có giá trị nhỏ nhất là −a2+b2+c và giá trị lớn nhất là a2+b2+c.

    3. Ví dụ minh họa

    Ví dụ 1: Tìm giá trị lớn nhất và nhỏ nhất của hàm số sau:

    a) y = 3sin(2x+1) – 7

    b) y=−2cos2x+π3+1

    Lời giải

    a) y = 3sin(2x+1) – 7

    Cách 1: Áp dụng công thức ta có: −3−7≤y≤3−7⇔−10≤y≤−4

    Cách 2: Giải chi tiết

    Ta có −1≤sin2x+1≤1∀x∈ℝ

    ⇔−3≤3sin2x+1≤3∀x∈ℝ⇔−10≤sin2x+1−7≤−4∀x∈ℝ⇔−10≤y≤−4

    Vậy giá trị lớn nhất của hàm số là -4 và giá trị nhỏ nhất của hàm số là -10.

    b) y=−2cos2x+π3+1

    Cách 1: Áp dụng công thức ta có: −2+1≤y≤1⇔−1≤y≤1.

    Cách 2: Giải chi tiết

    Ta có 0≤cos2x+π3≤1∀x∈ℝ

    ⇔0≤2cos2x+π3≤2∀x∈ℝ⇔−2≤−2cos2x+π3≤0∀x∈ℝ⇔−1≤−2cos2x+π3+1≤1∀x∈ℝ⇔−1≤y≤1

    Vậy giá trị lớn nhất của hàm số là 1 và giá trị nhỏ nhất của hàm số là -1.

    Ví dụ 2: Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số: y = 5sin2x – 12cosx + 2

    Lời giải

    Cách 1: Áp dụng công thức ta có:

    −52+122+2≤y≤52+122+2⇔−11≤y≤15

    Cách 2: Giải chi tiết

    Ta có: y = 5sin2x – 12cosx + 2

    ⇔y=13513sin2x−1213cos2x+2⇔y=13sin2xcosα−cos2xsinα+2

    ⇔y=13sin2x−α+2 với 513=cosα; 1213=sinα.

    Ta có −1≤sin2x−α≤1∀x∈ℝ

    ⇔−13≤13sin2x−α≤13∀x∈ℝ⇔−11≤13sin2x−α+2≤15∀x∈ℝ⇔−11≤y ≤15

    Vậy giá trị lớn nhất của hàm số là 15 và giá trị nhỏ nhất của hàm số là -11.

    4. Bài tập tự luyện

    Câu 1. Giá trị nhỏ nhất và giá trị lớn nhất của hàm số y=7−2cosx+π4lần lượt là:

    A. 4 và 7

    B. -2 và 7

    C. 5 và 9

    D. -2 và 2

    Câu 2. Giá trị nhỏ nhất và lớn nhất của hàm số y = 4cos2x – 3sin2x + 6 là:

    A. 3 và 10

    B. 1 và 11

    C. 6 và 10

    D. -1 và 13

    Câu 3. Giá trị lớn nhất và nhỏ nhất của hàm số y = 3 – 2|sinx| lần lượt là

    A. 1 và 0

    B. 3 và 2

    C. 3 và -2

    D. 3 và 1

    Đáp án:

    1 – C, 2 – B, 3 – D

    Xem thêm tổng hợp công thức môn Toán lớp 9 đầy đủ và chi tiết khác:

    Công thức giải phương trình lượng giác cơ bản

    Công thức, cách biến đổi biểu thức a sinx + b cosx

    Công thức, cách gộp nghiệm phương trình lượng giác

    Công thức hoán vị

    Công thức chỉnh hợp

    Tham khảo các loạt bài Toán 11 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 9,929 22/06/2022
    Tải về
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: