50 bài tập về Nhị thức Niu-tơn (có đáp án 2024) và cách giải

Nhị thức Niu-tơn và cách giải các dạng bài tập - Toán lớp 11

1. Lý thuyết

a) Định nghĩa:

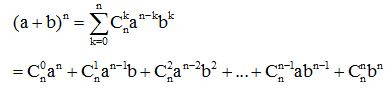
b) Nhận xét:

Trong khai triển Niu tơn (a + b)ⁿ có các tính chất sau

- Gồm có n + 1 số hạng

- Số mũ của a giảm từ n đến 0 và số mũ của b tăng từ 0 đến n

- Tổng các số mũ của a và b trong mỗi số hạng bằng n

- Các hệ số có tính đối xứng: $C_n^k=C_n^{n-k}$

- Quan hệ giữa hai hệ số liên tiếp: $C_n^k+C_n^{k+1}=C_{n+1}^{k+1}$

- Số hạng tổng quát thứ k + 1 của khai triển: $T_{k+1}=C_n^k{a}^{n-k}{b}^k$

Ví dụ:

Số hạng thứ nhất $T_1=T_{0+1}=C_n^0{a}^n$, số hạng thứ k: $T_k=T_{(k-1)+1}=C_n^{k-1}{a}^{n-k+1}{b}^{k-1}$

c) Hệ quả:

Ta có: ${(1+x)}^n=C_n^0+x{C}_n^1+x^2{C}_n^2+\mathrm{...}+x^n{C}_n^n$

Từ khai triển này ta có các kết quả sau

$\begin{array}{l}{C}_n^0+C_n^1+\mathrm{...}+C_n^n=2^n\\ C_n^0-C_n^1+C_n^2-\mathrm{...}+{(-1)}^n{C}_n^n=0\end{array}$

2. Các dạng bài tập

Dạng 1. Tìm số hàng chứa x^m trong khai triển

Phương pháp giải:

* Với khai triển (ax^p + bx^q)ⁿ (p, q là các hằng số)

Ta có: ${\left(a{x}^p+b{x}^q\right)}^n=\sum _{k=0}^n{C}_n^k{\left(a{x}^p\right)}^{n-k}{\left(b{x}^q\right)}^k$$=\sum _{k=0}^n{C}_n^k{a}^{n-k}{b}^k{x}^{np-pk+qk}$

Số hạng chứa x^m ứng với giá trị k thỏa mãn: np – pk + qk = m

Từ đó tìm $k=\frac{m-np}{q-p}$

Vậy hệ số của số hạng chứa x^m là: $C_n^k{a}^{n-k}.b^k$ với giá trị k đã tìm được ở trên.

* Với khai triển P(x) = (a + bx^p + cx^q)ⁿ (p, q là các hằng số)

Ta có: $P\left(x\right)={\left(a+b{x}^p+c{x}^q\right)}^n$$=\sum _{k=0}^n{C}_n^k{a}^{n-k}{\left(b{x}^p+c{x}^q\right)}^k$

$=\sum _{k=0}^n{C}_n^k{a}^{n-k}\sum _{j=0}^k{C}_k^j{\left(b{x}^p\right)}^{k-j}{\left(c{x}^q\right)}^j$

Từ số hạng tổng quát của hai khai triển trên ta tính được hệ số của x^m.

* Chú ý:

- Nếu k không nguyên hoặc k > n thì trong khai triển không chứa x^m, hệ số phải tìm bằng 0.

- Nếu hỏi hệ số không chứa x tức là tìm hệ số chứa x⁰.

Ví dụ minh họa:

Ví dụ 1: Tìm hệ số của x⁵ trong khai triển đa thức của: x(1 – 2x)⁵ + (1 + 5x)¹⁰.

Lời giải

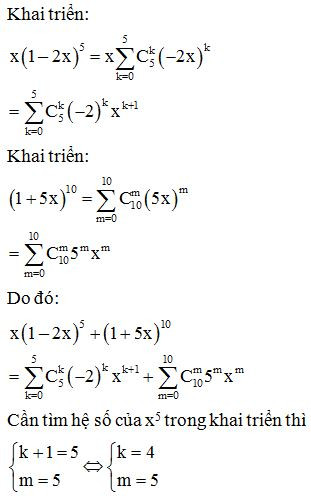
Vậy hệ số của đa thức trong khai triển là: $C_5^4{\left(-2\right)}^4+C_{10}^5{5}^5=787580$.

Ví dụ 2: Tìm hệ số không chứa x trong các khai triển sau ${\left(x^3-\frac{2}{x}\right)}^n$, biết rằng $C_n^{n-1}+C_n^{n-2}=78$ với x > 0.

Lời giải

Ta có: $C_n^{n-1}+C_n^{n-2}=78$ (Điều kiện: $n\ge 2;n\in \mathbb{N}$)

$\begin{array}{l}\iff \frac{n!}{\left(n-1\right)!.1!}+\frac{n!}{\left(n-2\right)!.2!}=78\\ \iff n+\frac{n\left(n-1\right)}{2}=78\\ \iff 2n+n^2-n=156\\ \iff n^2+n-156=0\\ \iff \left(n-12\right)\left(n+13\right)=0\\ \iff \left[\begin{array}{l}n=12\\ n=-13\left(Loại\right)\end{array}\right.\end{array}$

Do đó ta được khai triển:

$\begin{array}{l}{\left(x^3-\frac{2}{x}\right)}^{12}=\sum _{k=0}^{12}{C}_{12}^k{\left(x^3\right)}^{12-k}{\left(-\frac{2}{x}\right)}^k\\ =\sum _{k=0}^{12}{C}_{12}^k{\left(-2\right)}^k{x}^{36-3k}{x}^{-k}\\ =\sum _{k=0}^{12}{C}_{12}^k{\left(-2\right)}^k{x}^{36-4k}\end{array}$

Cần tìm hệ số không chứa x trong khai triển nên $36-4k=0\iff k=9$.

Vậy hệ số không chứa x của khai triển là: $C_{12}^9{\left(-2\right)}^9=-112640$.

Ví dụ 3: Tìm hệ số của x¹⁵ trong khai triển (1 – x + 2x²)¹⁰.

Lời giải

Ta có khai triển:

$\begin{array}{l}{\left(1–x+2x^2\right)}^{10}=\sum _{k=0}^{10}{C}_{10}^k{\left(-x+2x^2\right)}^k\\ =\sum _{k=0}^{10}{C}_{10}^k\sum _{j=0}^k{C}_k^j{\left(-x\right)}^{k-j}{\left(2x^2\right)}^j\\ =\sum _{k=0}^{10}\sum _{j=0}^k{C}_{10}^k{C}_k^j{\left(-1\right)}^{k-j}{.2}^j.x^{k+j}\end{array}$

Cần hệ số của x¹⁵ trong khai triển nên $\left\{\begin{array}{l}k+j=15\\ 0\le j\le k\le 10\\ j,k\in \mathbb{N}\end{array}\right.$

Trường hợp 1: k = 8; j = 7, ta được 1 hệ số là $C_{10}^8{C}_8^7{\left(-1\right)}^{8-7}{.2}^7=-46080$

Trường hợp 2: k = 9; j = 6, ta được 1 hệ số là $C_{10}^9{C}_9^6{\left(-1\right)}^{9-6}{.2}^6=-53760$

Trường hợp 3: k = 10; j = 5, ta được 1 hệ số là $C_{10}^{10}{C}_{10}^5{\left(-1\right)}^{10-5}{.2}^5=-8064$

Vậy hệ số của x¹⁵ trong khai triển là: – 46080 – 53760 – 8064 = –107904.

Dạng 2. Bài toán tính tổng

Phương pháp giải:

Dựa vào khai triển nhị thức Niu tơn

${(a+b)}^n$$=C_n^0{a}^n+a^{n-1}b{C}_n^1+a^{n-2}{b}^2{C}_n^2+\mathrm{...}+b^n{C}_n^n$.

Ta chọn những giá trị a, b thích hợp thay vào đẳng thức trên.

Một số kết quả ta thường hay sử dụng:

$\begin{array}{l}{C}_n^k=C_n^{n-k}\\ C_n^k+C_n^{k+1}=C_{n+1}^{k+1}\\ C_n^0+C_n^1+\mathrm{...}+C_n^n=2^n\\ C_n^0-C_n^1+C_n^2-\mathrm{...}+{\left(-1\right)}^n{C}_n^n=0\\ {\left(1+x\right)}^n=\sum _{k=0}^n{C}_n^k{x}^k\end{array}$

Ví dụ minh họa:

Ví dụ 1: Tính tổng

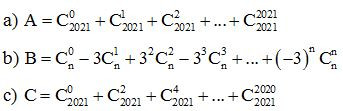
Lời giải

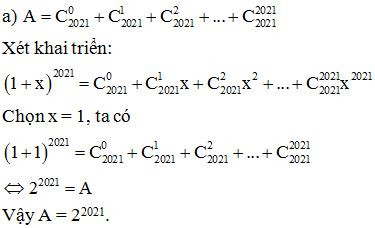
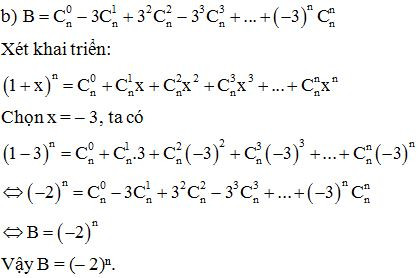
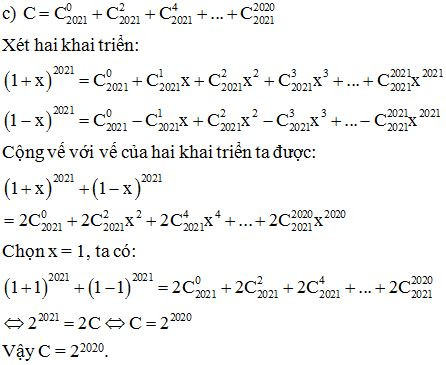
Ví dụ 2: Tìm số n thỏa mãn:

a) $C_n^0+2C_n^1+4C_n^2+\mathrm{...}+2^n{C}_n^n=243$

b) $C_{2n+1}^1+C_{2n+1}^3+C_{2n+1}^5+\mathrm{...}+C_{2n+1}^{2n+1}=4096$

Lời giải

Ví dụ 3. Cho khai triển (1 – 2x)²⁰ = a₀ +a₁x + a₂x² + … + a₂₀x²⁰. Giá trị của a₀ + a₁ + a₂ + … + a₂₀ bằng:

A. 1

B. 3²⁰

C. 0

D. – 1

Lời giải

Chọn A

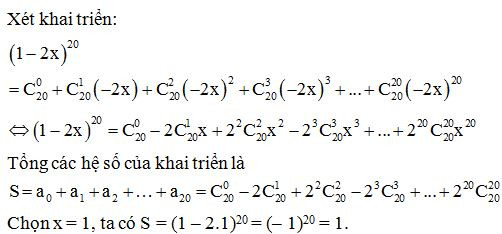
3. Bài tập tự luyện

Câu 1. Có bao nhiêu số hạng trong khai triển nhị thức (2x – 3)²⁰²⁰

A. 2021.

B. 2019.

C. 2018.

D. 2020.

Câu 2. Hệ số x⁶ trong khai triển (1 – 2x)¹⁰ thành đa thức là:

A. – 13440.

B. – 210.

C. 210.

D. 13440.

Câu 3. Số hạng không chứa x trong khai triển nhị thức Niu tơn ${\left(x^2+\frac{2}{x}\right)}^{12}$ ($x\ne 0$) là

A. $2^4.C_{12}^5$.

B. $C_{12}^8$.

C. $2^4.C_{12}^4$.

D. $2^8.C_{12}^8$.

Câu 4. Tìm số hạng không chứa x trong khai triển nhị thức Niu tơn ${\left(x-\frac{2}{x^2}\right)}^{21}$$\left(x\ne 0,n\in {\mathbb{N}}^{*}\right)$

A. $2^7{C}_{21}^7$.

B. $2^8{C}_{21}^8$.

C. $-2^8{C}_{21}^8$.

D. $-2^7{C}_{21}^7$.

Câu 5. Tìm hệ số của số hạng chứa x⁶ trong khai triển x³(1 – x)⁸

A. – 28.

B. 70.

C. – 56.

D. 56.

Câu 6. Trong khai triển biểu thức (x + y)²¹ , hệ số của số hạng chứa x¹³y⁸ là:

A. 116280.

B. 293930.

C. 203490.

D. 1287.

Câu 7. Hệ số của x⁶ trong khai triển ${\left(\frac{1}{x}+x^3\right)}^{10}$ bằng:

A. 792.

B. 210.

C. 165.

D. 252.

Câu 8. Trong khai triển ${\left(x+\frac{2}{\sqrt[]{x}}\right)}^6$, hệ số của x³, (x > 0) là:

A. 60.

B. 80.

C. 160.

D. 240.

Câu 9. Tìm hệ số của x⁵ trong khai triển P(x) = (x + 1)⁶ + (x + 1)⁷ + ... + (x + 1)¹²

A. 1715.

B. 1711.

C. 1287.

D. 1716.

Câu 10. Tìm số hạng không chứa x trong khai triển ${\left(x^2-\frac{1}{x}\right)}^n$ biết $A_n^2-C_n^2=105$

A. – 3003.

B. – 5005.

C. 5005.

D. 3003.

Câu 11. Tính tổng $S=C_{10}^0+2.C_{10}^1+2^2.C_{10}^2+\mathrm{...}+2^{10}.C_{10}^{10}.$

A. S = 2¹⁰.

B. S = 4¹⁰.

C. S = 3¹⁰.

D. S = 3¹¹.

Câu 12. Tổng $C_{2016}^1+C_{2016}^2+C_{2016}^3+\mathrm{...}+C_{2021}^{2021}$ bằng

A. 4²⁰²¹.

B. 2²⁰²¹ + 1.

C. 4²⁰²¹ – 1.

D. 2²⁰²¹ – 1.

Câu 13. Số tập con của tập hợp gồm 2022 phần tử là

A. 2022.

B. 2²⁰²² .

C. 2022².

D. 2.2022.

Câu 14. Trong khai triển (x – 2)¹⁰⁰ = a₀ + a₁x¹ + ... + a₁₀₀x¹⁰⁰. Tổng hệ số: a₀ + a₁+ ... + a₁₀₀ là

A. – 1.

B. 1.

C. 3¹⁰⁰.

D. 2¹⁰⁰.

Câu 15. Tổng $C_{2n}^0+C_{2n}^2+C_{2n}^4+\mathrm{...}+C_{2n}^{2n}$ bằng:

A. 2^n-2.

B. 2^n-1.

C. 2^2n-2.

D. 2^2n-1.

Bảng đáp án

1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
A	D	D	D	C	C	B	A	A	D	C	D	B	B	D

Xem thêm các dạng bài tập Toán lớp 9 có đáp án và lời giải chi tiết khác:

Cách giải phương trình, bất phương trình tổ hợp chi tiết nhất

Xác định biến cố và tính xác suất của biến cố chi tiết nhất

Trọn bộ công thức tính xác suất đầy đủ, chi tiết nhất

Phương pháp quy nạp toán học và cách giải

Dãy số và cách giải các dạng bài tập