Nội dung bài viết

    Xem thêm

    Bài 9 trang 84 Toán 7 Tập 2 | Chân trời sáng tạo Giải Toán lớp 7

    Lời giải Bài 9 trang 84 Toán 7 Tập 2 sách Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 7.

    1 516 28/02/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Giải Toán 7 Chân trời sáng tạo Bài tập cuối chương 8 

    Bài 9 trang 84 Toán 7 Tập 2:

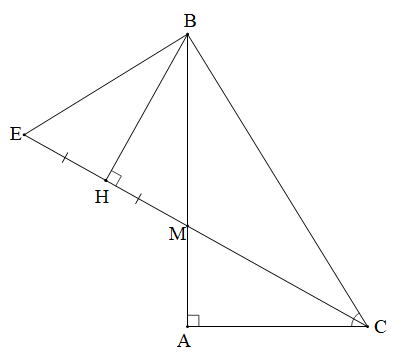
    Cho tam giác ABC vuông tại A. Tia phân giác của góc C cắt AB ở M. Từ B kẻ BH vuông góc với đường thẳng CM (H ∈ CM). Trên tia đối của tia HC lấy điểm E sao cho HE = HM.

    a) Chứng minh rằng tam giác MBE cân.

    b) Chứng minh rằng EBH^=ACM^.

    c) Chứng minh rằng EB ⊥ BC.

    Lời giải:

    GT

    ∆ABC vuông tại A,

    Tia phân giác của góc C cắt AB ở M,

    BH ⊥ CM (H ∈ CM).

    E thuộc tia đối của tia HC, HE = HM

    KL

    a) ∆MBE cân.

    b) EBH^=ACM^

    c) EB ⊥ BC.

     

    Giải Toán 7 (Chân trời sáng tạo): Bài tập cuối chương 8 (ảnh 1) 

    a) Vì E thuộc tia đối của tia HC và HE = HM (giả thiết) nên H là trung điểm của ME.

    Mà BH ⊥ CM tại H (giả thiết)

    Do đó BH là đường trung trực của EM

    Suy ra BM = BE.

    Tam giác MBE có BM = BE nên tam giác MBE cân tại B.

    Vậy tam giác MBE cân tại B.

    b)

    +) Xét ∆BEH (vuông tại H) và ∆BMH (vuông tại H) có:

    BH là cạnh chung,

    BE = BM (chứng minh câu a)

    Do đó ∆BEH = ∆BMH (cạnh huyền – cạnh góc vuông)

    Suy ra HBE^=HBM^ (hai góc tương ứng) (1).

    +) Xét ∆BHM vuông tại H có:

    HBM^+BMH^=90° (trong tam giác vuông, hai góc nhọn phụ nhau)

    Suy ra HBM^=90°−BMH^  (2)

    Xét ∆ACM vuông tại A có:

    ACM^+CMA^=90° (trong tam giác vuông, hai góc nhọn phụ nhau)

    Suy ra ACM^=90°−CMA^  (3)

    Mà BMH^=CMA^ (hai góc đối đỉnh) (4)

    Từ (2), (3), (4) suy ra HBM^=ACM^  (5).

    Từ (1) và (5) suy ra HBE^=ACM^.

    Vậy EBH^=ACM^

    c) Vì CM là tia phân giác của BCA^ (giả thiết) nên ACM^=12BCA^  (6)

    Lại có HBE^=HBM^ (chứng minh câu b)

    Nên BH là tia phân giác của EBM^ do đó EBH^=12EBM^  (7)

    Mà EBH^=ACM^ (chứng minh câu b) (8)

    Từ (6), (7) và (8) ta có BCA^=EBM^ 

    Xét tam giác ACB vuông tại A có:

    ABC^+BCA^=90° (trong tam giác vuông, hai góc nhọn phụ nhau)

    Do đó ABC^+EBM^=90°

    Hay EBC^=90°, từ đó ta có EB ⊥ BC.

    Vậy EB ⊥ BC.

    Xem thêm lời giải bài tập Toán lớp 7 Chân trời sáng tạo hay, chi tiết khác: 

    Bài 1 trang 84 Toán 7 Tập 2: Cho tam giác ABC cân tại A (A^<90°). Hai đường cao BE và CF cắt nhau tại H. a) Chứng minh rằng ∆BEC = ∆CFB...

    Bài 2 trang 84 Toán 7 Tập 2: Cho tam giác ABC vuông tại A, vẽ đường cao AH. Trên tia đối của tia HA lấy điểm M sao cho H là trung điểm của AM...

    Bài 3 trang 84 Toán 7 Tập 2: Cho tam giác ABC vuông tại A (AB < AC), vẽ đường cao AH. Trên tia đối của tia HC lấy điểm D sao cho HD = HC...

    Bài 4 trang 84 Toán 7 Tập 2: Cho tam giác ABC vuông tại A (AB < AC). Trên cạnh BC lấy điểm N sao cho BA = BN. Kẻ BE ⊥ AN (E ∈ AN)...

    Bài 5 trang 84 Toán 7 Tập 2: Cho tam giác ABC nhọn (AB < AC), vẽ đường cao AH. Đường trung trực của cạnh BC cắt AC tại M, cắt BC tại N...

    Bài 6 trang 84 Toán 7 Tập 2: Cho tam giác nhọn MNP. Các trung tuyến ME và NF cắt nhau tại G. Trên tia đối của tia FN lấy điểm D sao cho FD = FN...

    Bài 7 trang 84 Toán 7 Tập 2: Cho tam giác ABC vuông tại A có AB=12AC, AD là tia phân giác  BAC^(D ∈ BC). Gọi E là trung điểm của AC...

    Bài 8 trang 84 Toán 7 Tập 2: Ở Hình 1, cho biết AE = AF và ABC^=ACB^. Chứng minh rằng AH là đường trung trực của BC...

    Bài 9 trang 84 Toán 7 Tập 2: Cho tam giác ABC vuông tại A. Tia phân giác của góc C cắt AB ở M. Từ B kẻ BH vuông góc với đường thẳng CM (H ∈ CM)...

    Bài 10 trang 84 Toán 7 Tập 2: Trên đường thẳng a lấy ba điểm phân biệt I, J, K (J ở giữa I và K). Kẻ đường thẳng b vuông góc với a tại J...

    Xem thêm lời giải bài tập Toán lớp 7 Chân trời sáng tạo hay, chi tiết khác: 

    Bài 10: Hoạt động thực hành và trải nghiệm. Làm giàn hoa tam giác để trang trí lớp học

    Bài tập cuối chương 8

    Câu hỏi trang 85 Toán 7 Tập 2

    Bài 1: Làm quen với biến cố ngẫu nhiên

    Bài 2: Làm quen với xác suất của biến cố ngẫu nhiên

     

    Tham khảo các loạt bài Toán 7 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 516 28/02/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: