Lý thuyết Ôn tập chương 3 (mới 2024 + Bài Tập) - Toán 9

Lý thuyết Toán 9 Ôn tập chương 3

Bài giảng Toán 9 Ôn tập chương 3

A. Lý thuyết

1. Góc ở tâm

Góc ở tâm là góc có đỉnh trùng với tâm của đường tròn.

• Hai cạnh của góc ở tâm cắt đường tròn tại hai điểm, do đó chia đường tròn thành hai cung.

+ Cung nhỏ: cung nằm bên trong góc (với góc α (0 < α < 180°)).

+ Cung lớn: Cung nằm bên ngoài góc.

• Cung AB được kí hiệu là $\stackrel{⏜}{AB}$. Để phân biệt hai cung có chung các mút là A và B như hình vẽ (0 < α < 180°), ta kí hiệu: $\stackrel{⏜}{AmB}, \stackrel{⏜}{AnB}$

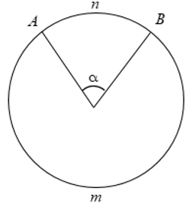
Trong đó: $\stackrel{⏜}{AnB}$ là cung nhỏ, $\stackrel{⏜}{AmB}$ là cung lớn.

Với α = 180° thì mỗi cung là một nửa đường tròn.

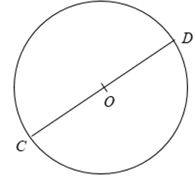
• Cung nằm bên trong góc gọi là cung bị chắn.

Khi đó, $\stackrel{⏜}{AnB}$ là cung bị chắn bởi góc AOB hay góc AOB chắn cung nhỏ $\stackrel{⏜}{AnB}$.

2. Số đo cung

• Số đo của cung nhỏ bằng số đo góc ở tâm chắn cung đó.

• Số đo của cung lớn bằng hiệu giữa 360° và số đo cung nhỏ (có chung hai mút với cung lớn).

• Số đo của nửa đường tròn bằng 180°.

Số đo của cung AB được kí hiệu là sđ $\stackrel{⏜}{AB}$.

3. Liên hệ giữa cung và dây

a) Định lí 1

Với hai cung nhỏ trong một đường tròn hay trong hai đường tròn bằng nhau:

- Hai cung bằng nhau căng hai dây bằng nhau.

- Hai dây bằng nhau căng hai cung bằng nhau.

b) Định lí 2

Với hai cung nhỏ trong một đường tròn hay trong hai đường tròn bằng nhau:

- Cung lớn hơn căng dây lớn hơn.

- Dây lớn hơn căng cung lớn hơn.

c) Mở rộng

Trong một đường tròn:

- Hai cung bị chắn giữa hai dây song song thì bằng nhau.

- Đường kính đi qua điểm chính giữa của một cung thì đi qua trung điểm của dây căng cung ấy.

- Đường kính đi qua trung điểm của một dây (không đi qua tâm) thì đi qua điểm chính giữa của cung bị căng bởi dây ấy.

- Đường kính đi qua điểm chính giữa của một cung thì vuông góc với dây căng cung ấy và ngược lại.

4. Góc nội tiếp

a. Định nghĩa

- Góc nội tiếp là góc có đỉnh nằm trên đường tròn và hai cạnh chứa hai dây cung của đường tròn đó.

- Cung bị chắn là cung nằm bên trong góc.

b. Định lí

Trong một đường tròn, số đo của góc nội tiếp bằng nửa số đo của cung bị chắn.

c. Hệ quả

Trong một đường tròn:

- Các góc nội tiếp bằng nhau chắn các cung bằng nhau.

- Các góc nội tiếp cùng chắn một cung hoặc chắn các cung bằng nhau thì bằng nhau.

- Góc nội tiếp (nhỏ hơn hoặc bằng 90°) có số đo bằng nửa số đo của góc ở tâm cùng chắn một cung.

- Góc nội tiếp chắn nửa đường tròn là góc vuông.

5. Góc tạo bởi tiếp tuyến và dây cung

a) Định nghĩa

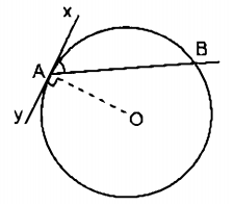
- Góc tạo bởi tia tiếp tuyến và dây cung là góc có đỉnh nằm trên đường tròn, một cạnh là một tia tiếp tuyến còn cạnh kia chứa dây cung của đường tròn.

- Cung nằm bên trong là cung bị chắn.

b) Định lí

Số đo của góc tạo bởi tiếp tuyến và dây cung bằng nửa số đo của cung bị chắn.

6. Góc có đỉnh ở bên trong đường tròn

- Góc có đỉnh nằm bên trong đường tròn được gọi là góc có đỉnh ở bên trong đường tròn.

- Định lí: Số đo của góc có đỉnh ở bên trong đường tròn bằng nửa tổng số đo hai cung bị chắn.

Trong hình vẽ trên, $\widehat{BEC}$ là góc có đỉnh nằm ở bên trong đường tròn chắn hai cung là .

Do đó,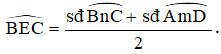

7. Góc có đỉnh nằm bên ngoài đường tròn

- Góc có đỉnh ở bên ngoài đường tròn là góc có đỉnh nằm ngoài đường tròn và các cạnh đều có điểm chung với đường tròn.

- Định lí: Số đo của góc có đỉnh ở bên ngoài đường tròn bằng nửa hiệu số đo hai cung bị chắn.

Ví dụ 2. Cho đường tròn (O) có hai dây AB và CD cắt nhau tại E (điểm E nằm bên ngoài đường tròn) như hình vẽ.

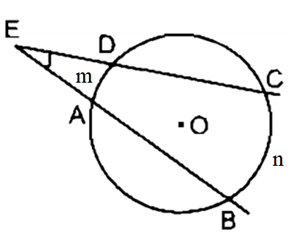
Trong hình vẽ trên, $\widehat{BEC}$ là góc có đỉnh nằm ở bên ngoài đường tròn chắn hai cung là $\stackrel{⏜}{BnC},\stackrel{⏜}{AmD}$.

Do đó,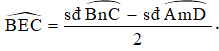

8. Tứ giác nội tiếp

a) Định nghĩa

Một tứ giác có bốn đỉnh nằm tên một đường tròn được gọi là tứ giác nội tiếp đường tròn (gọi tắt là tứ giác nội tiếp)

b) Định lí về tứ giác nội tiếp

- Trong một tứ giác nội tiếp, tổng số đo hai góc đối diện bằng 180°.

- Nếu một tứ giác có tổng số đo hai góc đối diện bằng 180° thì tứ giác đó nội tiếp được đường tròn.

c) Dấu hiệu nhận biết tứ giác nội tiếp

- Tứ giác có tổng hai góc đối bằng 180°.

- Tứ giác có góc ngoài tại một đỉnh bằng góc trong của đỉnh đối diện.

- Tứ giác có bốn đỉnh cách đều một điểm (mà ta có thể xác định được). Điểm đó là tâm của đường tròn ngoại tiếp tứ giác đó.

- Tứ giác có hai đỉnh kề nhau cùng nhìn một cạnh chứa hai đỉnh còn lại dưới một góc α.

- Chú ý: Để chứng minh một tứ giác là tứ giác nội tiếp ta có thể chứng minh tứ giác đó là một trong các hình sau: Hình chữ nhật, hình vuông, hình thang cân.

d) Định lí về đa giác nội tiếp

- Bất kì đa giác đều nào cũng có một và chỉ một đường tròn ngoại tiếp, có một và chỉ một đường tròn nội tiếp.

- Trong tam giác đều, tâm của đường tròn ngoại tiếp trùng với tâm của đường tròn nội tiếp và được gọi là tâm của đa giác đều.

- Tâm này là giao điểm hai đường trung trực của hai cạnh hoặc là hai đường phân giác của hai góc.

e) Công thức mở rộng

- Bán kính đường tròn ngoại tiếp đa giác là khoảng cách từ tâm đến đỉnh.

- Bán kính đường tròn nội tiếp đa giác là khoảng cách từ tâm O đến một cạnh.

Cho n-giác đều cạnh a. Khi đó:

- Chu vi của đa giác: 2p = na (p là nửa chu vi).

- Mỗi góc ở đỉnh của đa giác có số đo bằng $\frac{(n-2).{180}^o}{n}$.

- Mỗi góc ở tâm của đa giác có số đo bằng $\frac{{360}^o}{n}$.

- Bán kính đường tròn ngoại tiếp: $R=\frac{a}{2\sin \frac{{180}^o}{n}}$$\Rightarrow a=2R.\sin \frac{{180}^o}{n}$

- Bán kính đường tròn nội tiếp:

$$\begin{gathered} r=\frac{a}{2\tan \frac{{180}^o}{n}} \\ \Rightarrow a=2r.\tan \frac{{180}^o}{n} \end{gathered}$$

- Liên hệ giữa bán kính đường tròn ngoại tiếp và nội tiếp: $R^2-r^2=\frac{a^2}{4}$.

- Diện tích đa giác đều: $S=\frac{1}{2}nar$.

10. Độ dài đường tròn

“Độ dài đường tròn” hay còn được gọi là “chu vi đường tròn” được kí hiệu là C.

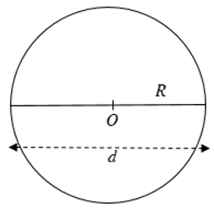
Công thức tính chu vi hình tròn: C = 2πR hoặc C = πd.

Trong đó: C là độ dài đường tròn;

R là bán kính đường tròn;

d là đường kính của đường tròn;

π (đọc là “pi”) là kí hiệu của một số vô tỉ mà giá trị gần đúng thường được lấy là π ≈ 3,14.

11. Độ dài cung tròn

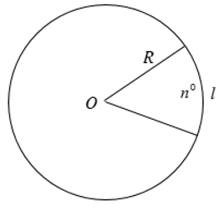
12. Diện tích hình tròn

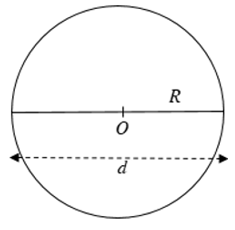
Công thức diện tích hình tròn là:

$S=\pi R^2=\pi \frac{d^2}{4}$

Trong đó: S là diện tích của hình tròn;

R là bán kính hình tròn;

d là đường kính của hính tròn.

13. Diện tích của hình quạt tròn

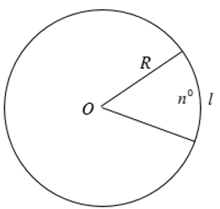
Công thức diện tích hình quạt tròn là:

$S=\frac{\pi R^{2}n}{360}=\frac{lR}{2}$

Trong đó: S là diện tích của hình quạt tròn;

R là bán kính đường tròn;

l là độ dài cung tròn n^o.

B. Bài tập tự luyện

Bài 1. Cho đường tròn (O; R). Trên đường tròn đó lấy hai điểm A và B sao cho $AB=R\sqrt{2}$. Tính số đo của hai cung AB.

Lời giải:

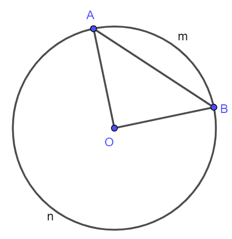
Đặt cung nhỏ AB là $\stackrel{⏜}{AmB}$ và cung lớn AB là $\stackrel{⏜}{AnB}$.

Hai điểm A và B nằm trên đường tròn (O; R) nên OA = OB = R

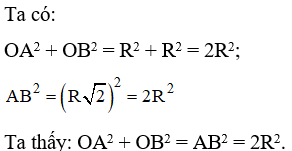
Nên ΔABC vuông tại A (theo định lý Py – ta – go đảo).

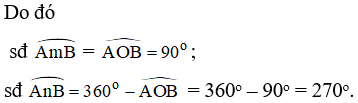
Vậy số đo cung nhỏ và cung lớn AB lần lượt là 90^o và 270^o.

Bài 2. Cho hai đường tròn đồng tâm (O; R) và $\left(O;\frac{R\sqrt{3}}{2}\right)$. Trên đường tròn nhỏ lấy một điểm M. Tiếp tuyến tại M của đường tròn nhỏ cắt đường tròn lớn tại A và B. Tia OM cắt đường tròn lớn tại C. Chứng minh rằng $\stackrel{⏜}{CA}=\stackrel{⏜}{CB}$.

Lời giải:

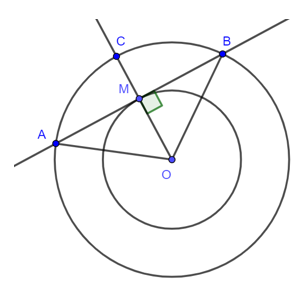
Tiếp tuyến tại M của đường tròn nhỏ cắt đường tròn lớn tại A và B hay AM là tiếp tuyến của đường tròn $\left(O;\frac{R\sqrt{3}}{2}\right)$ nên $OM\perp AB$.

Do đó OM là đường cao của ΔOAB.

Mặt khác, ΔOAB có OA = OB = R nên ΔOAB cân tại O.

Xét ΔOAB cân tại O có OM là đường cao nên OM cũng là đường phân giác hay $\widehat{AOM}=\widehat{BOM}$

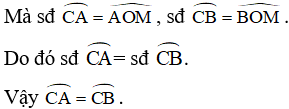
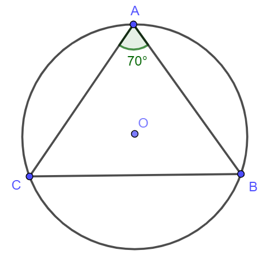
Bài 3. Cho tam giác ABC cân tại A nội tiếp trong đường tròn (O). Biết $\widehat{A}={70}^o$. Hãy so sánh các cung nhỏ AB, AC và BC.

Lời giải:

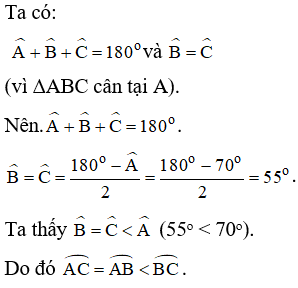
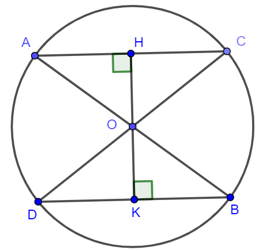
Bài 4. Cho đường tròn tâm O đường kính AB. Từ A và B vẽ hai dây cung AC và BD song song vs nhau. Qua O vẽ đường thẳng vuông góc AC tại M và BD tại N. So sánh hai cung AC và BD.

Lời giải:

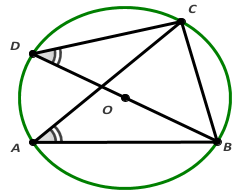
Bài 5. Cho ∆ABC nhọn nội tiếp đường tròn (O) đường kính BD. Biết $\widehat{BAC}$ = 45^o. Tính số đo $\widehat{CBA}$.

Lời giải:

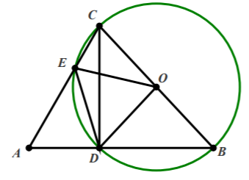
Bài 6. Cho ∆ABC nhọn có $\widehat{BAC}={60}^o$. Vẽ đường tròn đường kính BC tâm O cắt AB, AC lần lượt tại D và E. Tính số đo $\widehat{ODE}$.

Lời giải:

Bài 7. Cho nửa đường tròn (O) đường kính AB và dây AC căng cung AC có số đo bằng 60^o.

a) So sánh các góc tam giác ABC.

b) Gọi M, N lần lượt là điểm chính giữa của các cung AC và BC. Hai dây AN và BM cắt nhau tại I. Chứng minh rằng CI là phân giác góc ACB.

Lời giải:

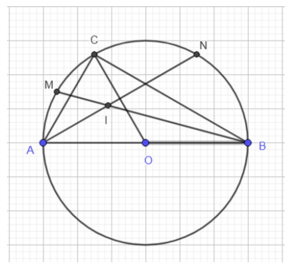
b) Ta có: $\widehat{ABM}=\widehat{CBM}$ (góc nội tiếp chắn cung AM bằng cung MC).

Nên BM là tia phân giác $\widehat{ABC}$.

Tương tự $\widehat{CAN}=\widehat{BAN}$ (góc nội tiếp cùng chắn cung CN bằng cung BN)

Nên AN là đường phân giác của $\widehat{BAC}$.

Ta thấy ΔABC có AN và BM là hai tia phân giác cắt nhau tại I nên CI là tia phân giác $\widehat{ACB}$ (tính chất ba đường phân giác của tam giác).

Bài 8. Hai tiếp tuyến tại A và B của đường tròn (O) cắt nhau tại P. Biết $\widehat{APB}$ = 55^o. Tính số đo cung lớn AB.

Lời giải:

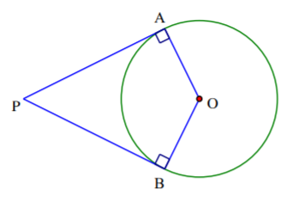
Bài 9. Cho đường tròn (O) đường kính AB. Trên tia đối của tia AB lấy điểm M. Kẻ tiếp tuyến MN với đường tròn (O) tại N. Vẽ NH vuông góc với AB.

Chứng minh $\widehat{MNA}=\widehat{ANH}$.

Lời giải:

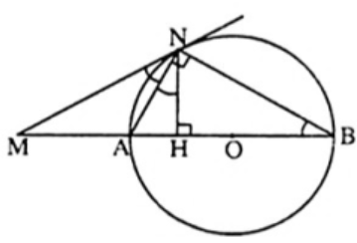
Bài 10. Cho hai tiếp tuyến tại A và B của đường tròn (O) cắt nhau tại M, biết $\widehat{AMB}={40}^o$.

a) Tính $\widehat{AMO}$ và $\widehat{AOM}$.

b) Tính số đo cung AB nhỏ và số đo cung AB lớn.

Lời giải:

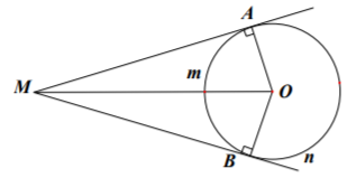
a) Do MA và MB là hai tiếp tuyến cắt nhau tại M.

Vậy số đo cung AB nhỏ và số đo cung AB lớn lần lượt là 140^o và 220^o.

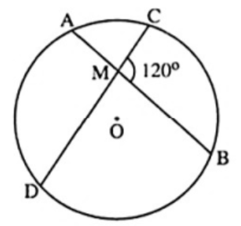
Bài 11. Cho đường tròn đường tròn (O) có hai dây AB và CD cắt nhau tại M như hình vẽ. Tính số đo của cung BD, biết $\widehat{AMB}={120}^o$.

Lời giải:

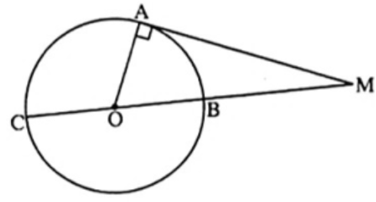
Bài 12. Cho đường tròn đường tròn (O) đường kính BC. Lấy điểm A nằm trên đường tròn, vẽ tiếp tuyến AM (A là tiếp điểm). Tính $\widehat{AMC}$, biết số đo cung AC là 120^o.

Lời giải:

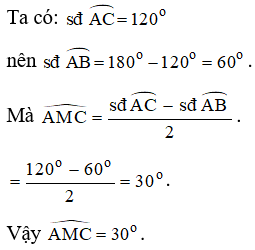
Bài 13. Từ điểm A nằm bên ngoài đường tròn (O) kẻ tiếp tuyến AB và cát tuyến ACD. Vẽ dây BM vuông góc với tia phân giác góc BAC tại H cắt CD tại E. Chứng minh BM là đường phân giác góc CBD.

Lời giải:

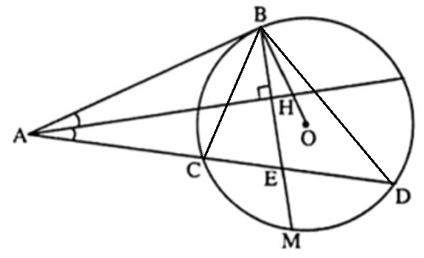
∆ABE có AH là đường phân giác đồng thời là đường cao nên ∆ABE cân tại đỉnh A.

Bài 14. Cho một góc vuông xOy, trên tia Ox lấy điểm A cố định, B là điểm chuyển động trên tia Oy. Tìm tập hợp các điểm C sao cho DABC vuông cân tại C.

Lời giải:

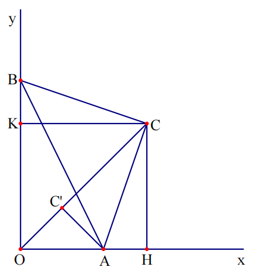
Do đó C thuộc tia phân giác Oz của góc vuông xOy.

- Phần đảo: Lấy điểm C bất kỳ thuộc tia C’z.

Vẽ đường thẳng vuông góc CA tại C cắt tia Oy tại B.

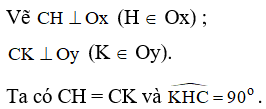
Xét ∆CAH vuông tại H và ∆CBK vuông tại K có:

CH = CK và $\widehat{CAH}=\widehat{CBK}$

Nên DCAH = DCBK (cạnh góc vuông – góc nhọn kề)

Suy ra CA = CB (hai cạnh tương ứng).

Do đó DABC vuông cân tại C.

- Kết luận: Tập hợp các điểm C là tia C’z của tia phân giác Oz của góc xOy.

Bài 15. Cho hình bình hành ABCD có cạnh AB cố định và cạnh CD chuyển động trên đường thẳng d song song với AB. Gọi I là trung điểm của CD. Tia AI cắt BC tại N. Tìm quỹ tích điểm N khi CD thay đổi trên đường thẳng d.

Lời giải:

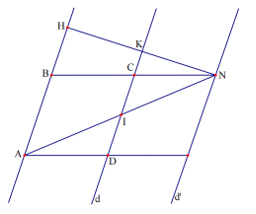
- Phần thuận:

Gọi khoảng cánh giữa đường thẳng AB và đường thẳng d là h không đổi.

Vì ABCD là hình bình hành nên BC // AD hay CN // AD.

Suy ra $\widehat{IDA}=\widehat{ICN}$ (hai góc so le trong).

Xét ∆IAD và ∆INC có:

$\widehat{AID}=\widehat{CIN}$ (đối đỉnh)

ID = IC (vì I là trung điểm của CD)

$\widehat{IDA}=\widehat{ICN}$ (cmt)

Do đó DIAD = DINC (g.c.g)

Suy ra CN = AD (hai cạnh tương ứng)

Mà AD = BC (vì tứ giác ABCD là hình bình hành).

Do đó CN = AD = BC.

Kẻ $NH\perp AB$, NH cắt đường thẳng d tại K.

∆NBH có CB = CN và CK // BH nên suy ra KH = KN.

Từ đó ta được HN = 2KH = 2h không đổi.

Khi CD chuyển động trên đường thẳng d thì với mọi vị trí của CD, điểm N luôn cách đường thẳng AB một khoảng 2h không đổi.

Vậy điểm N thuộc đường thẳng d’ song song với đường thẳng AB và cách đường thẳng AB một khoảng 2h không đổi.

- Phần đảo: Lấy điểm N bất kì trên đường thẳng d’.

Đường thẳng AN cắt đường thẳng d tại I, đường thẳng NB cắt đường thẳng d tại C.

Lấy điểm D đối xứng với C qua điểm I.

Ta cần chứng minh tứ giác ABCD là hình bình hành và I là trung điểm của CD.

Thật vậy, Kẻ $NH\perp AB$, NH cắt đường thẳng d tại K.

Ta có K là trung điểm của HN.

Do đó trong ∆HNB thì C là trung điểm của NB. 9

Trong ∆NAB có C là trung điểm của BN và IC // AB.

Nên IC là đường trung bình.

Từ đó ta được $IC=\frac{1}{2}AB$.

Vì D đối xứng với C qua I nên ta được ID = IC =$\frac{1}{2}AB$.

Do đó AB = CD.

Mà AB // CD nên tứ giác ABCD là hình bình hành và I là trung điểm của CD.

- Kết luận: Vậy quỹ tích điểm N là đường thẳng d’ song song với đường thẳng AB và cách đường thẳng AB một khoảng 2h không đổi.

Bài 16. Cho đường tròn (O; R) cố định. Lấy B, C là hai điểm cố định trên đường tròn và A là một điểm tuỳ ý trên đường tròn. Gọi M là điểm đối xứng của điểm C qua trung điểm I của AB. Tìm quỹ tích các điểm M.

Lời giải:

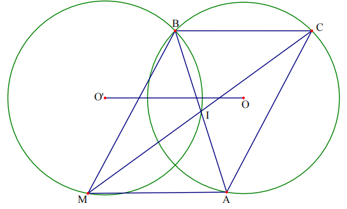
- Phần thuận:

Kẻ OO’// BC và OO’ = BC (O’ và B trên cùng một nửa mặt phẳng bờ AC).

Do đó ta được O’ cố định (vì O, B, C cố định và BC không đổi).

Xét tứ giác AMBC có:

IA = IB (vì I là trung điểm của AB)
IC = IM (vì điểm M đối xứng với B qua I)

Do đó tứ giác AMBC là hình bình hành.

Suy ra MA // BC và MA = BC

Mà OO’// BC và OO’ = BC

Do đó MA // OO’ và MA = OO’

Từ đó ta được tứ giác AMO’O là hình bình hành.

Nên suy ra O’M = OA = R không đổi và O’ cố định.

Do đó khi A di động thì M di động theo nhưng M luôn cách O’ cố định một khoảng không đổi là O’M = OA = R.

Vậy M thuộc đường tròn tâm O’ bán kính OA = R.

- Phần đảo: Trên đường tròn (O’; R) lấy điểm M bất kỳ. Nối MB.

Qua C kẻ đường thẳng song song với BM cắt đường tròn (O) ở điểm thứ hai A. Ta dễ dàng chứng minh được M đối xứng với C qua trung điểm I của AB.

- Kết luận: Do đó khi A di động thì M di động theo nhưng M luôn cách O’ cố định một khoảng không đổi là O’M = OA= R.

Vậy quỹ tích điểm M là đường tròn tâm O’ bán kính OA = R.

Bài 17. Cho tam giác ABC nhọn, đường cao BM và CN cắt nhau tại H. Chứng minh các tứ giác AMHN và BNMC là những tứ giác nội tiếp.

Lời giải:

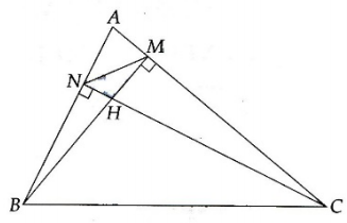
$\widehat{BMC}$ và $\widehat{BNC}$ cùng nhìn cạnh BC dưới một góc 90^o.

Do đó tứ giác BNMC là tứ giác nội tiếp.

Vậy các tứ giác AMHN và BNMC là những tứ giác nội tiếp.

Bài 18. Cho đường tròn (O) đường kính AB. Lấy điểm M thuộc đoạn thẳng OA, điểm N thuộc đường tròn (O). Từ A và B vẽ các tiếp tuyến Ax và By. Đường thẳng qua C và vuông góc với NM cắt Ax, By theo thứ tự tại C và D.

a) Chứng minh ACNM và BDNM là các tứ giác nội tiếp đường tròn.

b) Chứng minh ∆ANB đồng dạng với ∆CMD.

Lời giải:

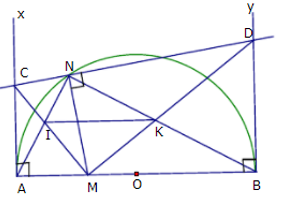
a) Xét tứ giác ACNM có:

$\widehat{MNC}={90}^o$ (vì $NM\perp CD$);

$\widehat{MAC}={90}^o$ (vì Ax là tiếp tuyến của nửa đường tròn (O)).

Do đó tứ giác ACNM nội tiếp đường tròn đường kính MC.

Xét tứ giác BDNM có:

$\widehat{MND}={90}^o$ (vì $NM\perp CD$);

$\widehat{MBD}={90}^o$ (vì By là tiếp tuyến của nửa đường tròn (O)).

Do đó tứ giác BDNM nội tiếp đường tròn đường kính MD.

Vậy các tứ giác ACNM và BDNM là các tứ giác nội tiếp đường tròn.

b) Xét ∆ANB và ∆CMD có:

$\widehat{BAN}=\widehat{DCM}$ (tứ giác ACNM nội tiếp)

$\widehat{ABN}=\widehat{CDM}$ (tứ giác BDNM nội tiếp)

Do đó ∆ANB ∆CMD (g.g).

Bài 19. Một đa giác đều nội tiếp đường tròn (O; R). Biết độ dài mỗi cạnh của nó là $R\sqrt{2}$. Hỏi đa giác đó là hình gì?

Lời giải:

Bài 20. Cho ∆ABC cân tại A có $\widehat{BAC}={120}^o$; BC = 6 cm. Tính bán kính đường tròn ngoại tiếp ∆ABC.

Lời giải:

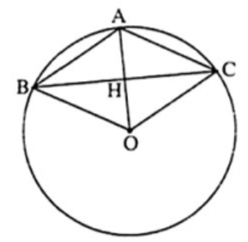
Xét ∆ABO và ∆ACO có:

AB = AC (vì ∆ABC cân tại A);

OB = OC (vì đều là bán kính đường tròn ngoại tiếp ∆ABC);

Cạnh OA chung.

Do đó ∆ABO = ∆ACO (c.c.c)

Suy ra $\widehat{BAO}=\widehat{CAO}$ mà $\widehat{BAO}+\widehat{CAO}=\widehat{BAC}={120}^o$.

Nên $\widehat{BAO}=\widehat{CAO}={60}^o$.

Mà ∆ACO cân tại O (vì OA = OC) nên ∆ACO đều.

Gọi AO cắt BC tại H ta có BH = CH = 3 cm.

∆ACO đều có $AO\perp CH$ nên HA = HO.

Áp dụng định lý Py – ta – go vào ∆CHO vuông tại H ($AO\perp CH$) có:

CH² + OH² = OC².

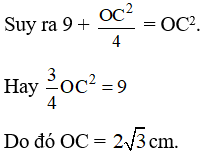
Vậy bán kính đường tròn ngoại tiếp ∆ABC là $2\sqrt{3}$ cm.

Bài 21. Cho tam giác ABC vuông tại A có AB = 3 cm, AC = 4 cm. Gọi R là bán kính đường tròn ngoại tiếp; r là bán kính đường tròn nội tiếp tam giác ABC. Tính tỉ số $\frac{r}{R}$.

Lời giải:

Áp dụng định lý Py – ta – go vào ∆ABC vuông tại A, ta có:

BC² = AB² + AC² = 3² + 4² = 25.

$\Rightarrow$ BC = 5 (cm).

Do đó bán kính đường tròn ngoại tiếp ∆ABC là:

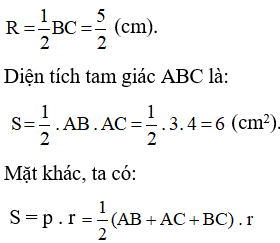
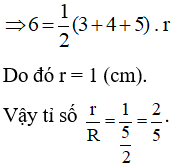
Bài 22. Cho đường tròn (O) bán kính OA. Từ trung điểm M của OA vẽ dây BC vuông góc OA. Biết độ dài đường tròn (O) là 4π (cm). Tính:

a) Bán kính đường tròn (O).

b) Độ dài hai cung BC của đường tròn.

Lời giải:

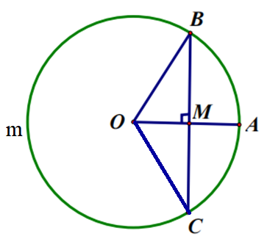
a) Độ dài bán kính đường tròn (O) là:

b) Áp dụng định lý Py – ta – go vào ∆BOM vuông tại M, ta có:

BM² + OM² = OB²

∆BOM vuông tại M nên $\sin \widehat{BOM}=\frac{BM}{OB}=\frac{\sqrt{3}}{2}$= 60^o.

∆OBC cân tại O (vì OB = OC) có OM là đường cao nên OM cũng là đường phân giác.

Suy ra $\widehat{BOC}=2\widehat{BOM}=$$2.{60}^o={120}^o$

Đặt cung lớn BC là $\stackrel{⏜}{BmC}$.

Số đo của cung lớn BC là:

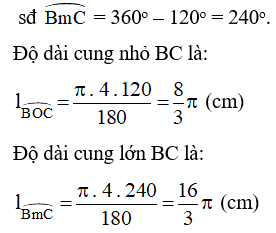
Vậy độ dài cung nhỏ và cung lớn BC lần lượt là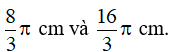

Bài 23. Tam giác ABC có AB = AC = 3 cm, $\widehat{A}={120}^o$. Tính độ dài đường tròn ngoại tiếp ∆ABC.

Lời giải:

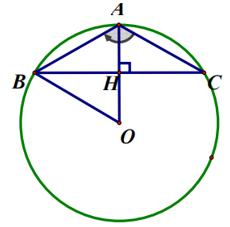
Ta có AB = AC nên A là điểm nằm chính giữa cung BC.

Suy ra:

$$\begin{gathered} AO\perp BC \\ \Rightarrow \widehat{BAH}=\widehat{HAC}={60}^o \end{gathered}$$

Do đó ∆ABH là nửa tam giác đều.

Nên AB = BO = 3 (cm).

Vậy độ dài đường tròn ngoại tiếp ∆ABC là: C = 2πR = 6π (cm).

Bài 24. Một tam giác đều và một hình vuông có cùng chu vi là 72 cm. Hỏi độ dài đường tròn ngoại tiếp hình nào lớn hơn? Lớn hơn bao nhiêu?

Lời giải:

* Xét tam giác ABC đều ngoại tiếp đường tròn (O) có chu vi 72 cm.

Kẻ AH là đường trung trực của ∆ABC tại H.

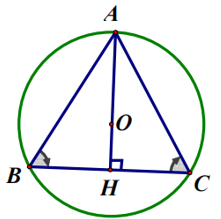
Độ dài cạnh của tam giác đều: 72 : 3 = 24 (cm)

Áp dụng định lý Py – ta – go vào ∆ABH vuông tại H, ta có:

AH² + BH² = AB²

Đường tròn (O) ngoại tiếp ∆ABC nên AH là đường trung trực của ∆ABC.

Mà ∆ABC đều nên AH cũng là đường trung tuyến.

Suy ra O cũng là trọng tâm của ∆ABC.

Do đó OA = $\frac{2}{3}$AH =$\frac{2}{3}.12\sqrt{3}=8\sqrt{3}$ = R.

Do đó độ dài đường tròn ngoại tiếp tam giác đều là:

C = 2πR = $16\sqrt{3}$π (cm).

* Xét hình vuông MNPQ ngoại tiếp đường tròn (O’) có chu vi 72 cm.

Nối N với Q.

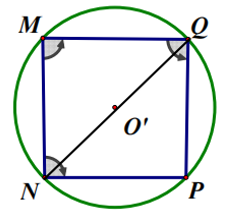
Độ dài các cạnh của hình vuông là: 72 : 4 = 18 (cm).

Áp dụng định lý Py – ta – go vào ∆NPQ vuông tại P, ta có:

NP² + PQ² = NQ²

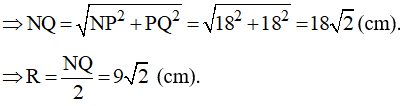
Do đó độ dài đường tròn ngoại tiếp hình vuông là:

Vậy độ dài đường tròn ngoại tiếp tam giác đều lớn hơn đường tròn ngoại tiếp hình vuông và lớn hơn:

Bài 25. Một hình tròn có diện tích S = 256π cm². Tính bán kính của hình tròn đó.

Lời giải:

Diện tích hình hình tròn là:

Vậy bán kính của hình tròn là 16 cm.

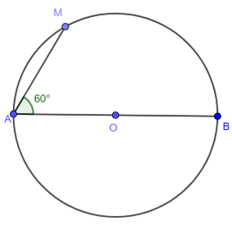
Bài 26. Cho đường tròn (O; 8cm) đường kính AB. Điểm M$\in$(O) sao cho $\widehat{BAM}={60}^o$. Tính diện tích hình quạt AOM.

Lời giải:

Bài 27. Cho đường tròn (O) đường kính AB. Lấy M thuộc đoạn AB, vẽ dây tại M. Giả sử AM = 2 cm và CD =$4\sqrt{3}$ cm. Tính:

a) Độ dài đường tròn (O) và diện tích hình tròn.

b) Độ dài cung CAD và diện tích hình quạt tròn giới hạn bởi hai bán kính OC, OD và cung nhỏ CD.

Lời giải:

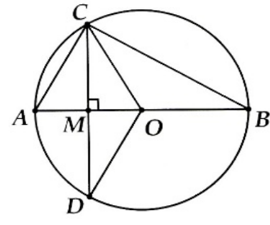
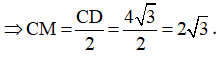
Theo định lý Py – ta – go, ta có: AC² = AM² + CM².

∆AMC có $\sin \widehat{CAM}=\frac{CM}{AC}$$=\frac{2\sqrt{3}}{4}=\frac{\sqrt{3}}{2}$$\Rightarrow \widehat{CA\text{}M}={60}^o$.

∆OAC cân tại O (vì OA = OC) có $\widehat{CA\text{}O}={60}^o$ nên ∆OAC đều.

Suy ra OA = AC = 4 (cm).

Độ dài đường tròn (O) là: C = 2πR = 8π (cm).

Diện tích hình tròn (O) là: S = πR² = 16π (cm²).

b) ∆OAC đều $\Rightarrow \widehat{A\text{}OC}={60}^o$.

∆OCD cân tại O có OM là đường cao nên OM cũng là đường phân giác hay :

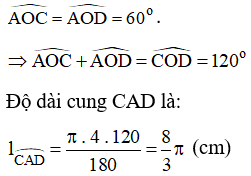
Diện tích hình quạt tròn giới hạn bởi hai bán kính OC, OD và cung nhỏ CD là:

$S=\frac{\frac{8}{3}\pi .4}{2}=\frac{16}{3}\pi \left(c{m}^2\right)$

Xem thêm các bài tổng hợp lý thuyết Toán lớp 9 đầy đủ, chi tiết khác:

Lý thuyết Cung chứa góc

Lý thuyết Tứ giác nội tiếp

Lý thuyết Đường tròn ngoại tiếp. Đường tròn nội tiếp

Lý thuyết Độ dài đường tròn, cung tròn

Lý thuyết Diện tích hình tròn, hình quạt tròn