Lý thuyết Cung chứa góc (mới 2024 + Bài Tập) - Toán 9

Lý thuyết Toán 9 Bài 6: Cung chứa góc

Bài giảng Toán 9 Bài 6: Cung chứa góc

A. Lý thuyết

1. Quỹ tích cung chứa góc

Với đoạn thẳng AB và góc α (0 < α < 180°) cho trước thì quỹ tích các điểm M thoả mãn $\widehat{AMB}=\alpha$ là hai cung chứa góc α dựng trên đoạn AB.

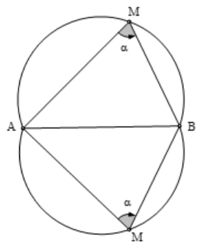
Lưu ý:

- Hai cung chứa góc α nói trên là hai cung tròn đối xứng nhau qua AB.

- Hai điểm A, B được coi là thuộc quỹ tích.

- Quỹ tích các điểm M nhìn đoạn thẳng AB cho trước dưới một góc vuông là đường tròn đường kính AB.

2. Cách vẽ cung chứa góc α

– Vẽ đường trung trực d của đoạn thẳng AB.

– Vẽ tia Ax sao cho $\widehat{BAx}=\alpha$.

– Vẽ đường thẳng Ay vuông góc với Ax. Gọi O là giao điểm của Ay với d.

– Vẽ cung AmB, tâm O, bán kính OA sao cho cung này nằm ở nửa mặt phẳng bờ AB không chứa tia Ax.

- $\stackrel{⏜}{AmB}$ được vẽ như trên là một cung chứa góc α.

Ta có hình vẽ:

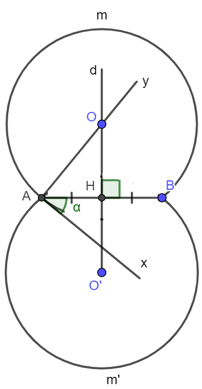
3. Cách giải bài toán quỹ tích

Muốn chứng minh quỹ tích (tập hợp) các điểm M thoả mãn tính chất T là một hình H nào đó, ta phải chứng minh hai phần:

– Phần thuận: Mọi điểm có tính chất T đều thuộc hình H.

– Phần đảo: Mọi điểm thuộc hình H đều có tính chất T.

– Kết luận: Quỹ tích các điểm M có tính chất T là hình H.

Ví dụ. Cho góc xOy cố định và điểm A cố định nằm trên tia Ox. B là điểm chuyển động trên tia Oy. Tìm tập hợp trung điểm M của AB.

Lời giải:

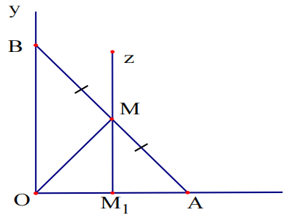
- Phần thuận:

+ Xét tam giác vuông OAB có OM = MA = MB

Nên ∆OAM cân tại M.

Mà OA cố định suy ra M nằm trên đường trung trực của đoạn thẳng OA.

- Phần đảo:

Lấy M bất kỳ thuộc tia M₁z, AM cắt Oy tại B.

Suy ra MO = MA $\Rightarrow \widehat{MAO}=\widehat{MOA}$.

Mặt khác $\widehat{OBM}=\widehat{BOM}$ (cùng phụ với góc $\widehat{MAO}=\widehat{MOA}$) suy ra MO = MB.

Suy ra MO = MA = MB.

Hay M là trung điểm của AB.

- Kết luận: Tập hợp các trung điểm M của AB là đường trung trực của đoạn OA.

B. Bài tập tự luyện

Bài 1. Cho một góc vuông xOy, trên tia Ox lấy điểm A cố định, B là điểm chuyển động trên tia Oy. Tìm tập hợp các điểm C sao cho DABC vuông cân tại C.

Lời giải:

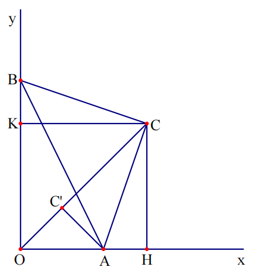
Do đó C thuộc tia phân giác Oz của góc vuông xOy.

- Phần đảo: Lấy điểm C bất kỳ thuộc tia C’z.

Vẽ đường thẳng vuông góc CA tại C cắt tia Oy tại B.

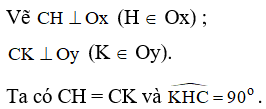
Xét ∆CAH vuông tại H và ∆CBK vuông tại K có:

CH = CK và $\widehat{CAH}=\widehat{CBK}$

Nên DCAH = DCBK (cạnh góc vuông – góc nhọn kề)

Suy ra CA = CB (hai cạnh tương ứng).

Do đó DABC vuông cân tại C.

- Kết luận: Tập hợp các điểm C là tia C’z của tia phân giác Oz của góc xOy.

Bài 2. Cho hình bình hành ABCD có cạnh AB cố định và cạnh CD chuyển động trên đường thẳng d song song với AB. Gọi I là trung điểm của CD. Tia AI cắt BC tại N. Tìm quỹ tích điểm N khi CD thay đổi trên đường thẳng d.

Lời giải:

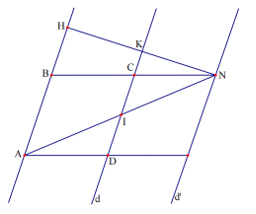
- Phần thuận:

Gọi khoảng cánh giữa đường thẳng AB và đường thẳng d là h không đổi.

Vì ABCD là hình bình hành nên BC // AD hay CN // AD.

Suy ra $\widehat{IDA}=\widehat{ICN}$ (hai góc so le trong).

Xét ∆IAD và ∆INC có:

$\widehat{AID}=\widehat{CIN}$ (đối đỉnh)

ID = IC (vì I là trung điểm của CD)

$\widehat{IDA}=\widehat{ICN}$ (cmt)

Do đó DIAD = DINC (g.c.g)

Suy ra CN = AD (hai cạnh tương ứng)

Mà AD = BC (vì tứ giác ABCD là hình bình hành).

Do đó CN = AD = BC.

Kẻ $NH\perp AB$, NH cắt đường thẳng d tại K.

∆NBH có CB = CN và CK // BH nên suy ra KH = KN.

Từ đó ta được HN = 2KH = 2h không đổi.

Khi CD chuyển động trên đường thẳng d thì với mọi vị trí của CD, điểm N luôn cách đường thẳng AB một khoảng 2h không đổi.

Vậy điểm N thuộc đường thẳng d’ song song với đường thẳng AB và cách đường thẳng AB một khoảng 2h không đổi.

- Phần đảo: Lấy điểm N bất kì trên đường thẳng d’.

Đường thẳng AN cắt đường thẳng d tại I, đường thẳng NB cắt đường thẳng d tại C.

Lấy điểm D đối xứng với C qua điểm I.

Ta cần chứng minh tứ giác ABCD là hình bình hành và I là trung điểm của CD.

Thật vậy, Kẻ $NH\perp AB$, NH cắt đường thẳng d tại K.

Ta có K là trung điểm của HN.

Do đó trong ∆HNB thì C là trung điểm của NB. 9

Trong ∆NAB có C là trung điểm của BN và IC // AB.

Nên IC là đường trung bình.

Từ đó ta được $IC=\frac{1}{2}AB$.

Vì D đối xứng với C qua I nên ta được ID = IC =$\frac{1}{2}AB$.

Do đó AB = CD.

Mà AB // CD nên tứ giác ABCD là hình bình hành và I là trung điểm của CD.

- Kết luận: Vậy quỹ tích điểm N là đường thẳng d’ song song với đường thẳng AB và cách đường thẳng AB một khoảng 2h không đổi.

Bài 3. Cho đường tròn (O; R) cố định. Lấy B, C là hai điểm cố định trên đường tròn và A là một điểm tuỳ ý trên đường tròn. Gọi M là điểm đối xứng của điểm C qua trung điểm I của AB. Tìm quỹ tích các điểm M.

Lời giải:

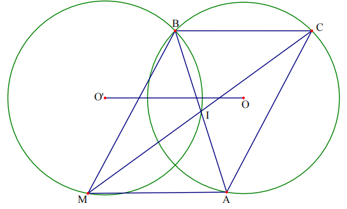
- Phần thuận:

Kẻ OO’// BC và OO’ = BC (O’ và B trên cùng một nửa mặt phẳng bờ AC).

Do đó ta được O’ cố định (vì O, B, C cố định và BC không đổi).

Xét tứ giác AMBC có:

IA = IB (vì I là trung điểm của AB)
IC = IM (vì điểm M đối xứng với B qua I)

Do đó tứ giác AMBC là hình bình hành.

Suy ra MA // BC và MA = BC

Mà OO’// BC và OO’ = BC

Do đó MA // OO’ và MA = OO’

Từ đó ta được tứ giác AMO’O là hình bình hành.

Nên suy ra O’M = OA = R không đổi và O’ cố định.

Do đó khi A di động thì M di động theo nhưng M luôn cách O’ cố định một khoảng không đổi là O’M = OA = R.

Vậy M thuộc đường tròn tâm O’ bán kính OA = R.

- Phần đảo: Trên đường tròn (O’; R) lấy điểm M bất kỳ. Nối MB.

Qua C kẻ đường thẳng song song với BM cắt đường tròn (O) ở điểm thứ hai A. Ta dễ dàng chứng minh được M đối xứng với C qua trung điểm I của AB.

- Kết luận: Do đó khi A di động thì M di động theo nhưng M luôn cách O’ cố định một khoảng không đổi là O’M = OA= R.

Vậy quỹ tích điểm M là đường tròn tâm O’ bán kính OA = R.

Xem thêm các bài tổng hợp lý thuyết Toán lớp 9 đầy đủ, chi tiết khác:

Lý thuyết Tứ giác nội tiếp

Lý thuyết Đường tròn ngoại tiếp. Đường tròn nội tiếp

Lý thuyết Độ dài đường tròn, cung tròn

Lý thuyết Diện tích hình tròn, hình quạt tròn

Lý thuyết Ôn tập chương 3