Nội dung bài viết

    Xem thêm

    Lý thuyết Một số hệ thức về cạnh và đường cao trong tam giác vuông (mới 2024 + Bài Tập) – Toán 9

    Lý thuyết Một số hệ thức về cạnh và đường cao trong tam giác vuông lớp 9 gồm lý thuyết chi tiết, ngắn gọn và bài tập tự luyện có lời giải chi tiết sẽ giúp học sinh nắm vững kiến thức trọng tâm Toán 9 Bài 1: Một số hệ thức về cạnh và đường cao trong tam giác vuông.

    1 6,421 21/12/2023
    Tải về
    Trang trước
    Chia sẻ
    Trang sau  

    Lý thuyết Toán 9 Bài 1: Một số hệ thức về cạnh và đường cao trong tam giác vuông

    A. Lý thuyết

    1. Hệ thức giữa cạnh góc vuông và hình chiếu của nó trên cạnh huyền

    Định lí 1. Trong một tam giác vuông, bình phương mỗi cạnh góc vuông bằng tích của cạnh huyền và hình chiếu của cạnh góc vuông đó trên cạnh huyền.

    Ví dụ 1. Tam giác ABC vuông tại A, đường cao AH.

    Khi đó, BH và CH lần lượt là hình chiếu của AB và AC trên BC.

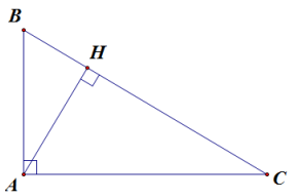
    Lý thuyết Một số hệ thức về cạnh và đường cao trong tam giác vuông chi tiết – Toán lớp 9 (ảnh 1)

    Ta có: AB2 = BC . BH; AC2 = BC . HC.

    2. Một số hệ thức liên quan tới đường cao

    Định lí 2. Trong một tam giác vuông, bình phương đường cao ứng với cạnh huyền bằng tích hai hình chiếu của hai cạnh góc vuông trên cạnh huyền.

    Ví dụ 2. Tam giác ABC vuông tại A, đường cao AH.

    Khi đó, BH và CH lần lượt là hình chiếu của AB và AC trên BC.

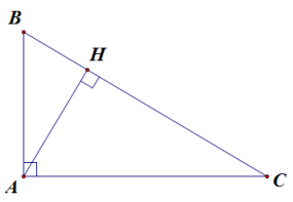
    Lý thuyết Một số hệ thức về cạnh và đường cao trong tam giác vuông chi tiết – Toán lớp 9 (ảnh 1)

    Ta có: AH2 = BH . HC.

    Định lí 3. Trong một tam giác vuông, tích hai cạnh góc vuông bằng tích của cạnh huyền và đường cao tương ứng.

    Ví dụ 3. Tam giác ABC vuông tại A, đường cao AH.

    Khi đó, BH và CH lần lượt là hình chiếu của AB và AC trên BC.

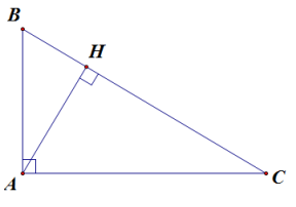
    Lý thuyết Một số hệ thức về cạnh và đường cao trong tam giác vuông chi tiết – Toán lớp 9 (ảnh 1)

    Ta có: AB . AC = BC . AH.

    Định lí 4. Trong một tam giác vuông, nghịch đảo của bình phương đường cao ứng với cạnh huyền bằng tổng các nghịch đảo của bình phương hai cạnh góc vuông.

    Ví dụ 4. Tam giác ABC vuông tại A, đường cao AH.

    Khi đó, BH và CH lần lượt là hình chiếu của AB và AC trên BC.

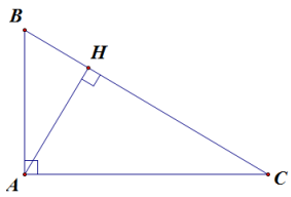
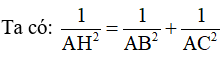
    Lý thuyết Một số hệ thức về cạnh và đường cao trong tam giác vuông chi tiết – Toán lớp 9 (ảnh 1)

    Lý thuyết Một số hệ thức về cạnh và đường cao trong tam giác vuông chi tiết – Toán lớp 9 (ảnh 1)

    B. Bài tập tự luyện

    Bài 1. Tìm độ dài x, y trong mỗi hình sau:

    a)

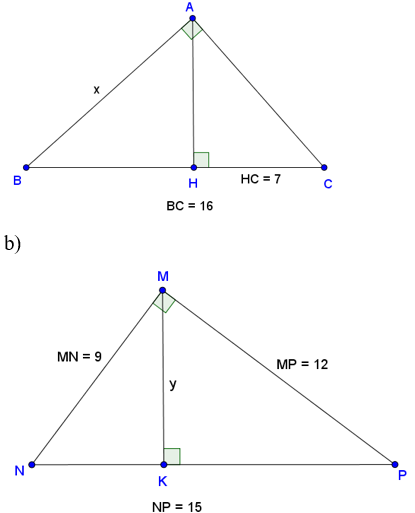
    Lý thuyết Một số hệ thức về cạnh và đường cao trong tam giác vuông chi tiết – Toán lớp 9 (ảnh 1)

    Lời giải:

    a) Tam giác ABC vuông tại A, đường cao AH.

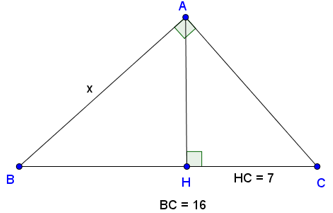
    Lý thuyết Một số hệ thức về cạnh và đường cao trong tam giác vuông chi tiết – Toán lớp 9 (ảnh 1)

    Ta có: BH = BC – HC = 16 – 7 = 9 (đvđd).

    AB2 = BC . BH = 16 . 9 = 144

    Suy ra: AB = 12 (đvđd).

    Vậy x = 12 (đvđd).

    b) Tam giác MNP vuông tại M, đường cao MK.

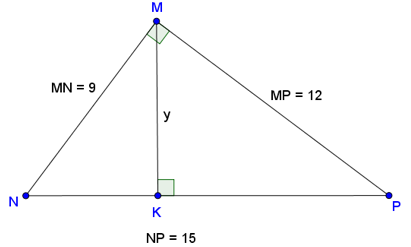
    Lý thuyết Một số hệ thức về cạnh và đường cao trong tam giác vuông chi tiết – Toán lớp 9 (ảnh 1)

    Ta có: AH . BC = AB . AC

    Suy ra: MK=MN . MPNP=9 . 1215=7,2 (đvđd).

    Vậy y = 7,2 (đvđd).

    Bài 2. Cho tam giác ABC vuông tại A, đường cao AH. Biết AB : BC = 3 : 5 và AB + BC = 16 cm. Tính độ dài các cạnh của tam giác ABC.

    Lời giải:

    Lý thuyết Một số hệ thức về cạnh và đường cao trong tam giác vuông chi tiết – Toán lớp 9 (ảnh 1)

    Theo giả thiết: AB : BC = 3 : 5 nên AB3=BC5.

    Áp dụng tính chất dãy tỉ số bằng nhau, ta có:

    AB3=BC5=AB+BC3+5=168=2.

    Do đó AB = 2.3 = 6 (cm); BC = 2.5 = 10 (cm).

    Tam giác ABC vuông tại A, theo định lý Py – ta – go, ta có:

    BC2 = AB2 + AC2

    Suy ra AC2 = BC2 − AC2 = 102 − 62 = 64.

    Do đó AC = 8 cm.

    Vậy độ dài các cạnh của tam giác ABC là: AB = 6 cm; AC = 8 cm; BC = 10 cm.

    Bài 3. Cho tam giác ABC vuông tại A, có AB = 3 cm, BC = 5 cm. AH là đường cao. Tính độ dài các cạnh AC, AH, BH, CH.

    Lời giải:

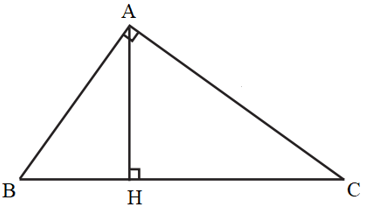
    Lý thuyết Một số hệ thức về cạnh và đường cao trong tam giác vuông chi tiết – Toán lớp 9 (ảnh 1)

    Áp dụng định lý Py – ta – go vào ∆ABC vuông tại A, ta có:

    BC2 = AB2 + AC2

    ⇔ AC2 = BC2 – AB2 = 52 – 32 = 16

    ⇔ AC = 4 (cm).

    Ta có:

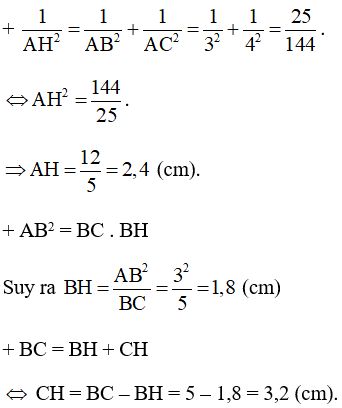
    Lý thuyết Một số hệ thức về cạnh và đường cao trong tam giác vuông chi tiết – Toán lớp 9 (ảnh 1)

    Vậy độ dài các cạnh AC = 4 cm, AH = 2,4 cm, BH = 1,8 cm, CH = 3,2 cm.

    Trắc nghiệm Toán lớp 9 Bài 1: Một số hệ thức về cạnh và đường cao trong tam giác vuông
    Câu 1: Tìm x, y trong hình vẽ sau:

    Trắc nghiệm Một số hệ thức về cạnh và đường cao trong tam giác vuông có đáp án – Toán lớp 9 (ảnh 2)

    A. x = 7,2; y = 11,8

    B. x = 7; y = 12

    C. x = 7,2; y = 12,8

    D. x = 7,2; y = 12

    Đáp án: C

    Giải thích:

    Trắc nghiệm Một số hệ thức về cạnh và đường cao trong tam giác vuông có đáp án – Toán lớp 9 (ảnh 3)

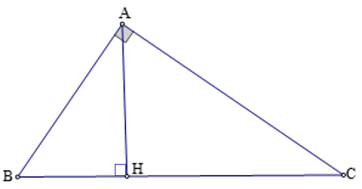
    Câu 2: Cho tam giác ABC vuông tại A, đường cao AH (như hình vẽ). Hệ thức nào sau đây là sai?

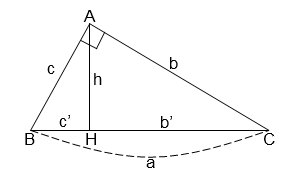
    Trắc nghiệm Một số hệ thức về cạnh và đường cao trong tam giác vuông có đáp án – Toán lớp 9 (ảnh 4)

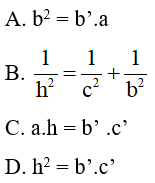
    Trắc nghiệm Một số hệ thức về cạnh và đường cao trong tam giác vuông có đáp án – Toán lớp 9 (ảnh 5)

    Đáp án: C

    Giải thích:

    Nhận thấy ah = bc nên phương án C là sai

    Câu 3: Cho tam giác ABC vuông tại A, chiều cao AH và AB = 5; AC = 12.

    Đặt BC = y, AH = x. Tính x, y

    A. x = 4; y = 119

    B. y=6013; x = 13

    C. x = 4; y = 13

    D.x=6013 ; y = 13

    Đáp án: D

    Giải thích:

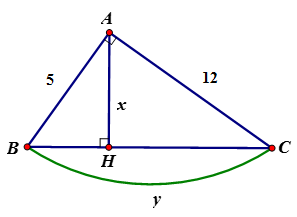
    Trắc nghiệm Một số hệ thức về cạnh và đường cao trong tam giác vuông có đáp án – Toán lớp 9 (ảnh 6)

    Trắc nghiệm Một số hệ thức về cạnh và đường cao trong tam giác vuông có đáp án – Toán lớp 9 (ảnh 7)

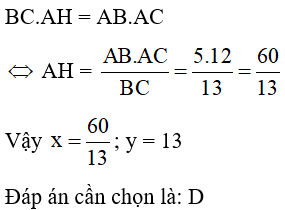
    Trắc nghiệm Một số hệ thức về cạnh và đường cao trong tam giác vuông có đáp án – Toán lớp 9 (ảnh 8)

    Câu 4: Tìm x, y trong hình vẽ sau:

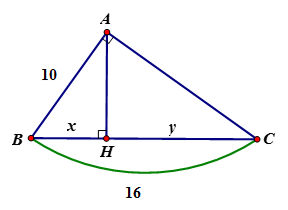
    Trắc nghiệm Một số hệ thức về cạnh và đường cao trong tam giác vuông có đáp án – Toán lớp 9 (ảnh 9)

    A. x= 6,5; y = 9,5

    B. x = 6,25; y = 9,75

    C. x = 9,25; y = 6,75

    D. x = 6; y = 10

    Đáp án: B

    Giải thích:

    Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ta có:

    AB2 = BH.BC

    ⇔BH=AB2BC=10016=6,25

    ⇒CH = BC – BH = 16 – 6,25 = 9,75

    Vậy x = 6,25; y = 9,75

    Câu 5: Tính x, y trong hình vẽ sau:

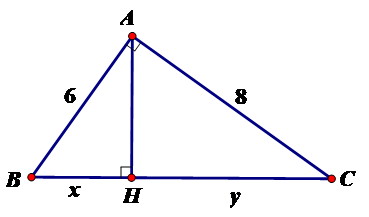
    Trắc nghiệm Một số hệ thức về cạnh và đường cao trong tam giác vuông có đáp án – Toán lớp 9 (ảnh 10)

    A. x = 3,6; y = 6,4

    B. y = 3,6; x = 6,4

    C. x = 4; y = 6

    D. x = 2,8; y = 7,2

    Đáp án: A

    Giải thích:

    Theo định lý Py-ta-go ta có

    BC2 = AB2 + AC2

    ⇔BC2 = 100 BC = 10

    Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ta có:

    AB2 = BH.BC

    ⇒BH=AB2BC=6210=3,6 hay x = 3,6

    ⇒CH = BC – BH = 10 – 3,6 = 6,4

    Câu 6: Cho tam giác ABC vuông tại A, AH⊥BC (H thuộc BC).

    Cho biết AB : AC = 4 : 5 và BC = 41 cm.

    Tính độ dài đoạn thẳng CH (làm tròn đến chữ số thập phân thứ nhất).

    A. CH≈2,5

    B. CH≈4

    C. CH≈3,8

    D. CH≈3,9

    Đáp án: D

    Giải thích:

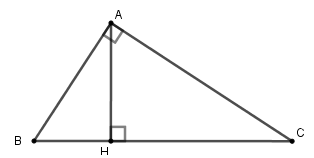
    Trắc nghiệm Một số hệ thức về cạnh và đường cao trong tam giác vuông có đáp án – Toán lớp 9 (ảnh 12)

    Ta có AB : AC = 4 : 5

    ⇔AB4=AC5⇒AB216=AC225=AB2+AC216+25=4141=1

    (Vì theo định lý Py-ta-go ta có

    AB2 + AC2 = BC2

    ⇔ AB2 + AC2 = 412= 41)

    Nên AB216=1⇒ AB2 = 16

    ⇒AB = 4; AC225=1⇒AC = 5

    Theo hệ thức lượng trong tam giác vuông ABC ta có:

    AC2 = CH.BC

    ⇒CH=AC2BC=2541≈3,9

    Vậy CH≈3,9

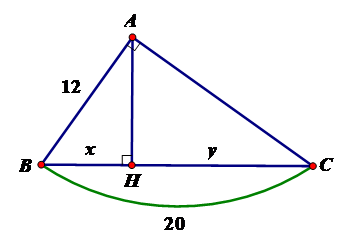
    Câu 7: Tính x, y trong hình vẽ sau:

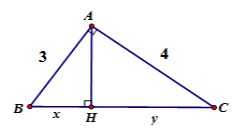
    Trắc nghiệm Một số hệ thức về cạnh và đường cao trong tam giác vuông có đáp án – Toán lớp 9 (ảnh 13)

    A. x = 3,2; y = 1,8

    B. x = 1,8; y = 3,2

    C. x = 2; y = 3

    D. x = 3; y = 2

    Đáp án: B

    Giải thích:

    Theo định lý Py-ta-go ta có

    BC2 = AB2 + AC2

    ⇔ BC2 = 25 BC = 5

    Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ta có:

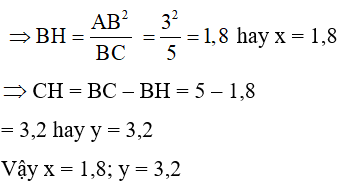
    Trắc nghiệm Một số hệ thức về cạnh và đường cao trong tam giác vuông có đáp án – Toán lớp 9 (ảnh 14)

    Câu 8: Tính diện tích hình thang ABCD có đường cao bằng 12cm, hai đường chéo AC và BD vuông góc với nhau, BD = 15cm.

    A. 150cm2

    B. 300cm2

    C. 125cm2

    D. 200cm2

    Đáp án: A

    Giải thích:

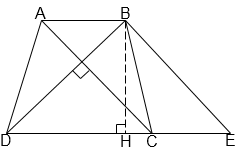
    Trắc nghiệm Một số hệ thức về cạnh và đường cao trong tam giác vuông có đáp án – Toán lớp 9 (ảnh 15)

    Qua B vẽ đường thẳng song song với AC, cắt DC ở E.

    Gọi BH là đường cao của hình thang.

    Ta có BE // AC, AC⊥BD nên BE⊥BD

    Áp dụng định lý Pytago vào tam giác vuông BDH,

    ta có: BH2 + HD2 = BD2

    ⇒122 + HD2 = 152

    ⇒ HD2 = 81⇒HD = 9cm

    Xét tam giác BDE vuông tại B:

    BD2 = DE.DH⇒152 = DE.9

    ⇒DE = 25cm

    Ta có: AB = CE nên:

    AB + CD = CE + CD = DE = 25cm

    Do đó SABCD = 25.12 : 2 = 150(cm2)

    Câu 9: Cho tam giác ABC vuông tại A, đường cao AH (như hình vẽ). Hệ thức nào sau đây là đúng?

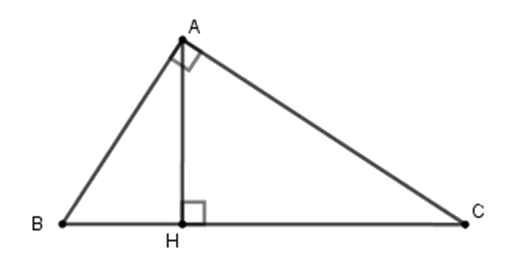
    Trắc nghiệm Một số hệ thức về cạnh và đường cao trong tam giác vuông có đáp án – Toán lớp 9 (ảnh 16)

    A. AH2 = AB. AC

    B. AH2 = BH.CH

    C. AH2 = AB.BH

    D. AH2 = CH.BC

    Đáp án: B

    Giải thích:

    Cho tam giác ABC vuông tại A, đường cao AH. Khi đó ta có hệ thức

    HA2 = HB.HC

    Câu 10: Cho tam giác ABC vuông tại A, đường cao AH. Biết AB : AC = 3 : 4 và AB + AC = 21

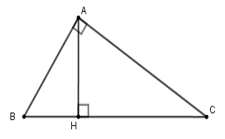
    Trắc nghiệm Một số hệ thức về cạnh và đường cao trong tam giác vuông có đáp án – Toán lớp 9 (ảnh 17)

    A. AB = 9; AC = 10; BC = 15

    B. AB = 9; AC = 12; BC = 15

    C. AB = 8; AC = 10; BC = 15

    D. AB = 8; AC = 12; BC = 15

    Đáp án: B

    Giải thích:

    Theo giả thiết AB : AC = 3 : 4

    Suy ra AB3=AC4=AB+AC3+4=3

    Do đó AB = 3.3 = 9 (cm);

    AC = 3.4 = 12 (cm)

    Tam giác ABC vuông tại A,

    theo định lý Pytago ta có:

    BC2 = AB2 + AC2 = 92 + 122 = 225,

    suy ra BC = 15cm

    Xem thêm các bài tổng hợp lý thuyết Toán lớp 9 đầy đủ, chi tiết khác:

    Tham khảo các loạt bài Toán 9 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 6,421 21/12/2023
    Tải về
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: