Lý thuyết Hình trụ - Diện tích xung quanh và thể tích của hình trụ (mới 2024 + Bài Tập) - Toán 9

Lý thuyết Toán 9 Bài 1: Hình trụ - Diện tích xung quanh và thể tích của hình trụ

Bài giảng Toán 9 Bài 1: Hình trụ - Diện tích xung quanh và thể tích của hình trụ

A. Lý thuyết

1. Hình trụ

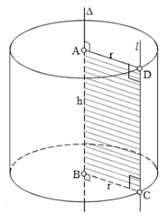
Khi quay hình chữ nhật ABCD một vòng quanh cạnh AB cố định, ta được một hình trụ.

- Hai hình tròn (A) và (B) bằng nhau và nằm trong hai mặt phẳng song song được gọi là hai đáy của hình trụ.

- Đường thẳng AB được gọi là trục của hình trụ.

- Mỗi vị trí của CD được gọi là một đường sinh. Các đường sinh vuông góc với hai mặt phẳng đáy. Độ dài của đường sinh là chiều cao của hình trụ.

Ví dụ 1. Một số vật có dạng hình trụ trong thực tế như: hộp sữa bột, cốc thủy tinh đựng nước, lon nước ngọt,…

Hình minh họa:

2. Cắt hình trụ bởi một mặt phẳng

- Khi cắt hình trụ bởi một mặt phẳng song song với đáy, thì phần mặt phẳng nằm trong hình trụ (mặt cắt – thiết diện) là một hình tròn bằng hình tròn đáy.

Ví dụ 2. Hình trụ bị cắt bởi mặt phẳng song song với hai đáy thì phần mặt phẳng nằm trong hình trụ (mặt cắt) là hình tròn (I) bằng hình tròn đáy (hình tròn (O) và (O’)) (như hình vẽ).

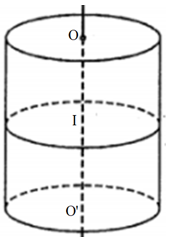
- Khi cắt hình trụ bởi một mặt phẳng song song với trục OO' thì mặt cắt là một hình chữ nhật.

Ví dụ 3. Hình trụ bị cắt bởi mặt phẳng ABCD, mặt phẳng này song song với OO’ thì mặt cắt là hình chữ nhật ABCD (như hình vẽ).

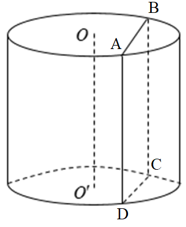
3. Diện tích và thể tích hình trụ

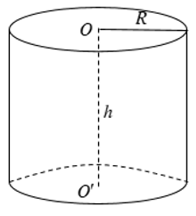
Cho hình trụ có bán kính đáy R và chiều cao h.

- Diện tích xung quanh: S_xq = 2πRh.

- Diện tích toàn phần: S_tp = 2πRh + 2πR².

- Thể tích: V = πR²h.

Ví dụ 4. Cho hình trụ có bán kính đáy R = 3 cm và chiều cao h = 6 cm. Tính diện tích xung quanh của hình trụ.

Lời giải:

Diện tích xung quanh của hình trụ là:

S_xq = 2πRh = 2π . 3 . 6 = 36 π (cm²).

B. Bài tập tự luyện

Bài 1. Cho hình trụ có bán kính đáy R =12 cm và diện tích toàn phần 672 cm². Tính chiều cao của hình trụ.

Lời giải:

Diện tích toàn phần của hình trụ là: 24πh + 2π . 12² = 672 π

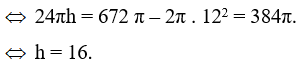
Vậy chiều cao của hình trụ là 16 cm.

Bài 2. Cho hình trụ bị cắt bỏ một phần OABB’A’O’ như hình vẽ. Tính thể tích phần còn lại.

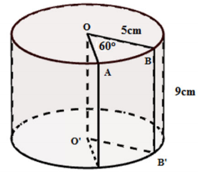
Lời giải:

Phần hình trụ bị cắt đi chiếm $\frac{{60}^o}{{360}^o}=\frac{1}{6}$ (hình trụ)

Thể tích phần còn lại là: V = $\frac{5}{6}\pi R^{2}h=\frac{5}{6}\pi .5^2.9$ = 187,5π (cm³).

Vậy thể tích phần còn lại là 187,5π cm³.

Bài 3. Một trục lăn có dạng hình trụ nằm ngang (như hình vẽ), hình trụ có diện tích một đáy S = 25π cm² và chiều cao h = 10 cm. Nếu trục lăn đủ 12 vòng thì diện tích tạo trên sân phẳng là bao nhiêu?

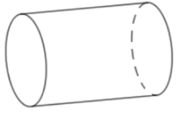
Lời giải:

Bán kính R của đường tròn đáy là πR² = 25π$\iff$ R = 5 cm.

Diện tích xung quanh của hình trụ là:

S_xq = 2πRh = 2π . 5 . 10 = 100 (cm²)

Vì trục lăn 12 vòng nên diện tích tạo trên sân phẳng là:

12 . 100π = 1200π (cm²)

Vậy nếu trục lăn đủ 12 vòng thì diện tích tạo trên sân phẳng là 1200π cm².

Xem thêm các bài tổng hợp lý thuyết Toán lớp 9 đầy đủ, chi tiết khác:

Lý thuyết Diện tích hình tròn, hình quạt tròn

Lý thuyết Ôn tập chương 3

Lý thuyết Hình nón – Hình nón cụt. Diện tích xung quanh và thể tích của hình nón, hình nón cụt

Lý thuyết Hình cầu. Diện tích mặt cầu và thể tích hình cầu

Lý thuyết Ôn tập chương 4