Lý thuyết Biến đổi đơn giản biểu thức căn thức bậc hai (mới 2024 + Bài Tập) – Toán 9

Lý thuyết Toán 9 Bài 6: Biến đổi đơn giản biểu thức căn thức bậc hai

A. Lý thuyết

1. Đưa một thừa số ra ngoài dấu căn

• Với a ≥ 0, b ≥ 0, ta có: $\sqrt{a^{2}b}=a\sqrt{b}$. Phép biến đổi này được gọi là phép đưa thừa số ra ngoài dấu căn.

• Đôi khi, ta phải biến đổi biểu thức dưới dấu căn về dạng thích hợp rồi mới thực hiện được phép đưa thừa số ra ngoài dấu căn.

• Có thể sử dụng phép đưa thừa số ra ngoài dấu căn để rút gọn biểu thức chứa căn thức bậc hai.

Ví dụ 1.

a) $\sqrt{3^2.5}=\sqrt{3^2}.\sqrt{5}=3\sqrt{5}$;

b) $$\begin{gathered} \sqrt{18}=\sqrt{9.2} \\ =\sqrt{3^2}.\sqrt{2}=3\sqrt{2} \end{gathered}$$

Tổng quát: Với hai biểu thức A, B mà B ≥ 0 ta có $\sqrt{A^2.B}=\left|A\right|\sqrt{B}$, tức là:

Nếu A ≥ 0 và B ≥ 0 thì $\sqrt{A^{2}B}=A\sqrt{B}$;

Nếu A < 0 và B ≥ 0 thì $\sqrt{A^{2}B}=-A\sqrt{B}$.

Ví dụ 2. Đưa thừa số ra ngoài căn:

a) $\sqrt{9x{y}^2}$với x ≥ 0, y < 0;

b) $\sqrt{20x^{2}y}$với x ≥ 0, y ≥ 0.

Lời giải:

a) $$\begin{gathered} \sqrt{9x{y}^2}=\sqrt{{\left(3y\right)}^{2}x} \\ =\left|3y\right|\sqrt{x}=-3y|\sqrt{x} \end{gathered}$$

(với x ≥ 0, y < 0);

b)

$$\begin{gathered} \sqrt{20x^{2}y}=\sqrt{4x^2.5y} \\ =\sqrt{{\left(2x\right)}^2.5y} \end{gathered}$$

$=\left|2x\right|\sqrt{5y}=x\sqrt{5y}$

(với x ≥ 0, y ≥ 0).

2. Đưa thừa số vào trong dấu căn

• Phép đưa thừa số ra ngoài dấu căn có phép biến đổi ngược với nó là phép đưa thừa số vào trong dấu căn.

Với A ≥ 0 và B ≥ 0 thì $A\sqrt{B}=\sqrt{A^{2}B}$.

Với A < 0 và B ≥ 0 thì $A\sqrt{B}=-\sqrt{A^{2}B}$.

Ví dụ 2. Đưa thừa số vào trong căn:

a) $5\sqrt{2}$;

b) $2a^2\sqrt{3a}$ với a ≥ 0.

Lời giải:

a) $$\begin{gathered} 5\sqrt{2}=\sqrt{5^2.2} \\ =\sqrt{25.2}=\sqrt{50} \end{gathered}$$

b)

$$\begin{gathered} 2a^2\sqrt{3a}=\sqrt{{\left(2a^2\right)}^2.3a} \\ =\sqrt{4a^4.3a}=\sqrt{12a^5} \end{gathered}$$

với a ≥ 0.

• Có thể sử dụng phép đưa thừa số vào trong (hoặc ra ngoài) dấu căn để so sánh các căn bậc hai.

Ví dụ 3. So sánh $3\sqrt{5}$ và $\sqrt{18}$.

Lời giải:

Ta có: $3\sqrt{5}=\sqrt{3^2.5}=\sqrt{45}$.

Vì $\sqrt{45}>\sqrt{18}$ nên $3\sqrt{5}>\sqrt{18}$.

3. Khử mẫu của biểu thức lấy căn

Tổng quát: Với các biểu thức A, B mà A. B ≥ 0 và B ≠ 0, ta có:

$\sqrt{\frac{A}{B}}=\frac{\sqrt{AB}}{\left|B\right|}$.

Ví dụ 4. Khử mẫu của biểu thức lấy căn

a) $\sqrt{\frac{3}{7}}$;

b) $\sqrt{\frac{11}{9a^3}}$ với a > 0

Lời giải:

a) $$\begin{gathered} \sqrt{\frac{3}{7}}=\sqrt{\frac{3.7}{7.7}} \\ =\frac{\sqrt{3.7}}{\sqrt{7^2}}=\frac{\sqrt{21}}{7} \end{gathered}$$

b) Vì a > 0 nên 3a > 0. Do đó |3a| = 3a;

Vì a > 0 nên 9a³ > 0. Do đó |9a³| > 9a³.

Khi đó,

$$\begin{gathered} \sqrt{\frac{11}{9a^3}}=\sqrt{\frac{11.9a^3}{9a^3.9a^3}} \\ =\frac{\sqrt{11a.9a^2}}{\sqrt{{\left(9a^3\right)}^2}}=\frac{\sqrt{11a}.\sqrt{9a^2}}{\left|9a^3\right|} \end{gathered}$$

$$\begin{gathered} =\frac{\left|3a\right|\sqrt{11a}}{\left|9a^3\right|}=\frac{3a\sqrt{11a}}{9a^3} \\ =\frac{\sqrt{11a}}{3a^2} \end{gathered}$$

4. Trục căn thức ở mẫu

Trục căn thức ở mẫu số là biến đổi để biểu thức đó mất căn thức ở mẫu số.

Tổng quát:

• Với các biểu thức A, B mà B > 0 ta có:

$\frac{A}{\sqrt{B}}=\frac{A\sqrt{B}}{B}$.

• Với các biểu thức A, B, C mà A ≥ 0, A ≠ B², ta có:

$\frac{C}{\sqrt{A}\pm B}=\frac{C(\sqrt{A}\mp B)}{A-B^2}$.

• Với các biểu thức A, B, C mà A ≥ 0, B ≥ 0, A ≠ B ta có:

$\frac{C}{\sqrt{A}\pm \sqrt{B}}=\frac{C(\sqrt{A}\mp \sqrt{B})}{A-B}$.

Ví dụ 5. Trục căn thức ở mẫu

a) $\frac{9}{\sqrt{2}-1}$;

b) $\frac{4}{\sqrt{7}-\sqrt{3}}$ .

Lời giải:

a) $\frac{9}{\sqrt{2}-1}=\frac{9(\sqrt{2}+1)}{(\sqrt{2}-1)(\sqrt{2}+1)}$

$$\begin{gathered} =\frac{9\sqrt{2}+9}{2-1}=\frac{9\sqrt{2}+9}{1} \\ =9\sqrt{2}+9 \end{gathered}$$

b) $\frac{4}{\sqrt{7}-\sqrt{3}}=\frac{4(\sqrt{7}+\sqrt{3})}{(\sqrt{7}+\sqrt{3})(\sqrt{7}-\sqrt{3})}$

$=\frac{4(\sqrt{7}+\sqrt{3})}{4}=\sqrt{7}+\sqrt{3}$

B. Bài tập tự luyện

Bài 1. So sánh:

a) $5\sqrt{2}$ và $\sqrt{38}$;

b) $4\sqrt{3}$ và 8.

Lời giải:

a) Ta có:

$$\begin{gathered} 5\sqrt{2}=\sqrt{5^2.2} \\ =\sqrt{25.2}=\sqrt{50} \end{gathered}$$

Vì 50 > 38 nên $\sqrt{50}>\sqrt{38}$hay $5\sqrt{2}>\sqrt{38}$.

Vậy $5\sqrt{2}>\sqrt{38}$.

b) Ta có:

$$\begin{gathered} 4\sqrt{3}=\sqrt{4^2.3} \\ =\sqrt{16.3}=\sqrt{48} \end{gathered}$$

$8=\sqrt{8^2}=\sqrt{64}$;

Vì 48 < 64 nên $\sqrt{48}<\sqrt{64}$ hay $4\sqrt{3}<8$.

Vậy $4\sqrt{3}<8$.

Bài 2. Rút gọn

a) $\frac{5}{x^2-y^2}\sqrt{\frac{2{(x+y)}^2}{5}}$ với x ≥ 0, y ≥ 0 và x ≠ y;

b) $\frac{3}{a-2}\sqrt{6a^2(a^2-4a+4)}$ với a > 2.

Lời giải:

a) Vì x ≥ 0 và y ≥ 0 nên x + y ≥ 0.

Khi đó, |x + y| = x + y.

Ta có:

$$\begin{gathered} \frac{5}{x^2-y^2}\sqrt{\frac{2{(x+y)}^2}{5}} \\ =\frac{5}{x^2-y^2}\sqrt{\frac{2}{5}.{(x+y)}^2} \end{gathered}$$

$$\begin{gathered} =\frac{5}{x^2-y^2}.\sqrt{\frac{2}{5}}.\sqrt{{(x+y)}^2} \\ =\frac{|x+y|}{(x+y)(x-y)}.5.\sqrt{\frac{2}{5}} \end{gathered}$$

$=\frac{(x+y)}{(x+y)(x-y)}.\sqrt{\frac{5^2.3}{5}}$

$=\frac{1}{x-y}.\sqrt{15}=\frac{\sqrt{15}}{x-y}$

b) Ta có: $\frac{3}{a-2}\sqrt{6a^2(a^2-4a+4)}$

$=\frac{3}{a-2}\sqrt{6a^2(a^2-2.2.a+2^2)}$

$=\frac{3}{a-2}\sqrt{6a^2{(a-2)}^2}$

$=\frac{3}{a-2}.\sqrt{6}.\sqrt{a^2}.\sqrt{{(a-2)}^2}$

$=\frac{3}{a-2}.\sqrt{6}.\left|a\right|.|a-2|$

Vì a > 2 nên a > 0 suy ra |a| = a.

Vì a > 2 nên |a – 2| = a – 2.

Do đó,

$$\begin{gathered} \frac{3}{a-2}.\sqrt{6}.\left|a\right|.|a-2| \\ =\frac{3}{a-2}.\sqrt{6}.a.(a-2) \end{gathered}$$

$=3a\sqrt{6}$

Vậy $\frac{3}{a-2}\sqrt{6a^2(a^2-4a+4)}=3a\sqrt{6}$ .

Trắc nghiệm Toán 9 Bài 6: Biến đổi đơn giản biểu thức chứa căn thức bậc hai

Câu 1: Đưa thừa số 5x$\sqrt{\frac{-12}{x^3}}$(x < 0) vào trong dấu căn ta được?

Hiển thị đáp án

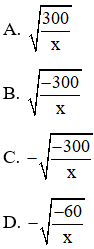
Đáp án: C

Giải thích:

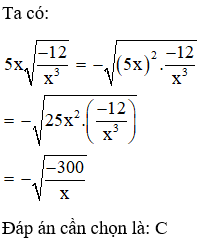
Câu 2: Khử mẫu biểu thức sau xy$\sqrt{\frac{4}{x^2{y}^2}}$với x > 0; y > 0 ta được:

Hiển thị đáp án

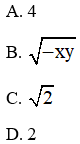
Đáp án: D

Giải thích:

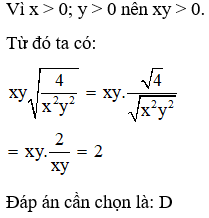
Câu 3: Cho các biểu thức A, B, C mà A, B, C > 0, khẳng định nào sau đây là đúng?

Hiển thị đáp án

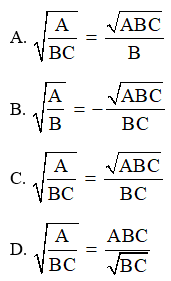
Đáp án: C

Giải thích:

Câu 4: Với hai biểu thức A, B mà A, B$\ge$ 0, ta có:

Hiển thị đáp án

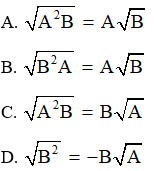
Đáp án: A

Giải thích:

Với hai biểu thức A, B mà A, B$\ge$ 0,

ta có:$\sqrt{A^{2}B}=\left|A\right|\sqrt{B}=A\sqrt{B}$

Câu 5: Đưa thừa số $\sqrt{144{\left(3+2a\right)}^4}$ ra ngoài dấu căn ta được?

A. 12(3 + 2a)⁴

B. 144(3 + 2a)²

C. −12(3 + 2a)²

D. 12(3 + 2a)²

Hiển thị đáp án

Đáp án: D

Giải thích:

Ta có:

$\sqrt{144{\left(3+2a\right)}^4}=\sqrt{{12}^2.{\left[{\left(3+2a\right)}^2\right]}^2}$

$=12.\left|{\left(3+2a\right)}^2\right|=12{(3+2a)}^2$

Câu 6: Khử mẫu biểu thức sau −xy$\sqrt{\frac{3}{xy}}$ với x < 0; y < 0 ta được:

Hiển thị đáp án

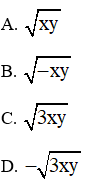
Đáp án: D

Giải thích:

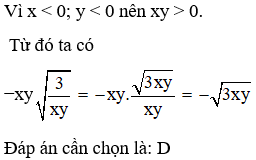
Câu 7: Đưa thừa số −7x$\sqrt{2xy}$(x$\ge$0, y$\ge$0) vào trong dấu căn ta được?

Hiển thị đáp án

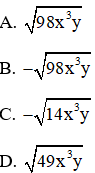
Đáp án: B

Giải thích:

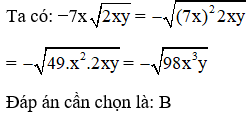
Câu 8: Đưa thừa số x$\sqrt{\frac{-35}{x}}$(x < 0) vào trong dấu căn ta được?

$$\begin{gathered} A.\sqrt{-35x} \\ B.-\sqrt{-35x} \\ C.\sqrt{35} \\ D.\sqrt{35x^2} \end{gathered}$$

Hiển thị đáp án

Đáp án: B

Giải thích:

Ta có

$$\begin{gathered} x\sqrt{\frac{-35}{x}}=-\sqrt{x^2\frac{-35}{x}} \\ =-\sqrt{-35x} \end{gathered}$$

Câu 9: Cho các biểu thức A, B mà A. B 0; B > 0, khẳng định nào sau đây là đúng?

Hiển thị đáp án

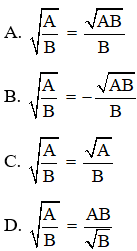
Đáp án: A

Giải thích:

Khử mẫu của biểu thức lấy căn

Với các biểu thức A, B mà A. B$\ge$ 0; B$\ne$0

Ta có :

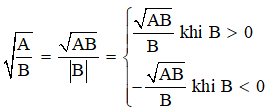
Đáp án cần chọn là: A

Câu 10: So sánh hai số $5\sqrt{3}$và $4\sqrt{5}$

Hiển thị đáp án

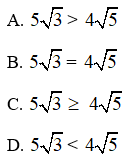
Đáp án: D

Giải thích:

Ta có:

$5\sqrt{3}=\sqrt{5^2.3}=\sqrt{25.3}=\sqrt{75}$

Vì 75 < 80 $\iff$$\sqrt{75}<\sqrt{80}$

$\iff$$5\sqrt{3} < 4\sqrt{5}$

Trắc nghiệm Toán 9 Bài 7: Biến đổi đơn giản biểu thức chưa căn thức bậc hai (Tiếp theo)

Câu 1: Phương trình

$\frac{2}{3}\sqrt{9x-9}-\frac{1}{4}\sqrt{16x-16}+27\sqrt{\frac{x-1}{81}}=4$

có mấy nghiệm?

A. 1

B. 0

C. 3

D. 2

Hiển thị đáp án

Đáp án: A

Giải thích:

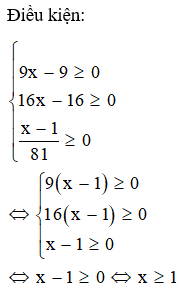
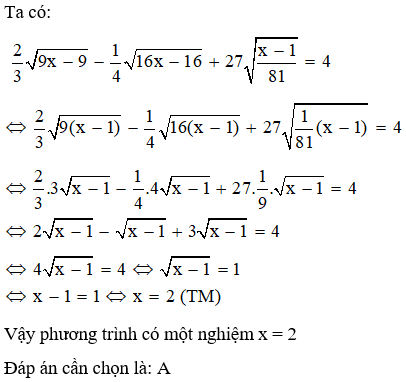
Câu 2: Rút gọn biểu thức

$7\sqrt{x}+11y\sqrt{36x^5}-2x^2\sqrt{16x{y}^2}-\sqrt{25x}$

với x$\ge$ 0; y$\ge$ 0 ta được kết quả là:

Hiển thị đáp án

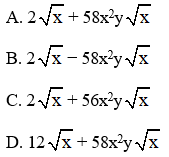
Đáp án: A

Giải thích:

Câu 3: Rút gọn biểu thức

$5\sqrt{a}+6\sqrt{\frac{a}{4}}-a\sqrt{\frac{4}{a}}+5\sqrt{\frac{4a}{25}}$

với a > 0, ta được kết quả là:

Hiển thị đáp án

Đáp án: B

Giải thích:

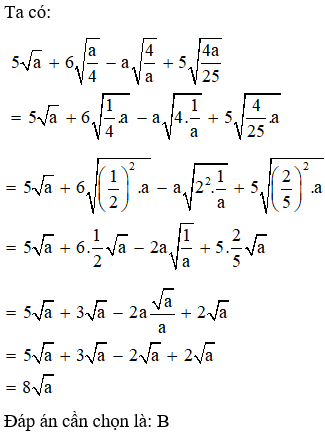
Câu 4: Trục căn thức ở mẫu biểu thức $\frac{6}{\sqrt{x}+\sqrt{2y}}$ với a$\ge$0; a$\ge$4 ta được:

Hiển thị đáp án

Đáp án: C

Giải thích:

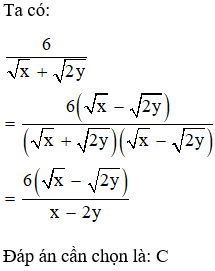
Câu 5: Trục căn thức ở mẫu biểu thức $\frac{2a}{2-\sqrt{a}}$ với a$\ge$0; a$\ne$4 ta được:

$$\begin{gathered} A.\frac{-2a\sqrt{a}+4a}{4-a} \\ B.\frac{2a\sqrt{a}-4a}{4-a} \\ C.\frac{2a\sqrt{a}+4a}{4-a} \\ D.-\frac{2a\sqrt{a}+4a}{4-a} \end{gathered}$$

Hiển thị đáp án

Đáp án: C

Giải thích:

Ta có:

$$\begin{gathered} \frac{2a}{2-\sqrt{a}} \\ =\frac{2a(2+\sqrt{a})}{(2-\sqrt{a})(2+\sqrt{a})} \\ =\frac{2a\sqrt{a}+4a}{4-a} \end{gathered}$$

Câu 6: Tính giá trị biểu thức

$\left(\frac{10+2\sqrt{10}}{\sqrt{5}+\sqrt{2}}+\frac{\sqrt{30}-\sqrt{6}}{\sqrt{5}-\sqrt{1}}\right):\frac{1}{2\sqrt{5}-\sqrt{6}}$

A. 28

B. 14

C. −14

D. 15

Hiển thị đáp án

Đáp án: B

Giải thích:

Câu 7: Trục căn thức ở mẫu biểu thức $\frac{3}{6+\sqrt{3a}}$với a$\ge$0; a$\ne$12 ta được:

Hiển thị đáp án

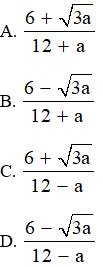
Đáp án: D

Giải thích:

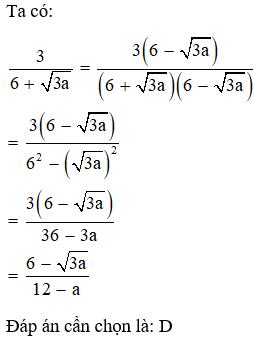
Câu 8: Cho ba biểu thức P =$x\sqrt{y}+y\sqrt{x}$; Q = $x\sqrt{x}+y\sqrt{y}$; R = x – y. Biểu thức nào bằng với biểu thức $\left(\sqrt{x}-\sqrt{y}\right)\left(\sqrt{x}+\sqrt{y}\right)$ với x, y không âm?

A. P

B. Q

C. R

D. P – Q

Hiển thị đáp án

Đáp án: C

Giải thích:

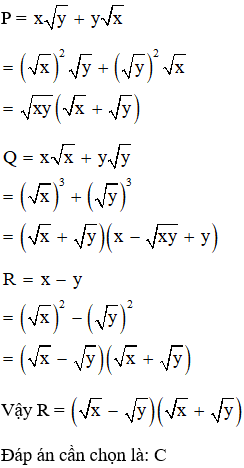
Câu 9: Trục căn thức ở mẫu biểu thức$\frac{4}{3\sqrt{x}+2\sqrt{y}}$ với x$\ge$0; y$\ge$0; x$\ne \frac{4}{9}y$ ta được:

Hiển thị đáp án

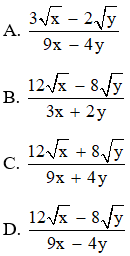
Đáp án: C

Giải thích:

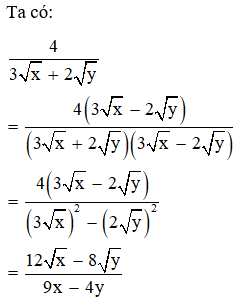
Câu 10: Số nghiệm của phương trình $\sqrt{9x^2-16}=3\sqrt{3x-4}$ là:

A. 1

B. 0

C. 3

D. 2

Hiển thị đáp án

Đáp án: D

Giải thích:

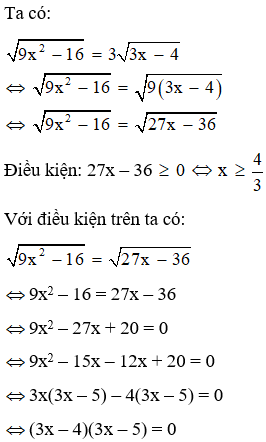
Xem thêm các bài tổng hợp lý thuyết Toán lớp 9 đầy đủ, chi tiết khác:

Lý thuyết Rút gọn biểu thức chứa căn thức bậc hai

Lý thuyết Căn bậc ba

Lý thuyết Ôn tập chương 1

Lý thuyết Căn bậc hai

Lý thuyết Căn thức bậc hai và hằng đẳng thức căn bậc hai(A^2)= |A|