Lý thuyết Hình cầu. Diện tích mặt cầu và thể tích hình cầu (mới 2024 + Bài Tập) - Toán 9

Lý thuyết Toán 9 Bài 3: Hình cầu. Diện tích mặt cầu và thể tích hình cầu

Bài giảng Toán 9 Bài 3: Hình cầu. Diện tích mặt cầu và thể tích hình cầu

A. Lý thuyết

1. Hình cầu

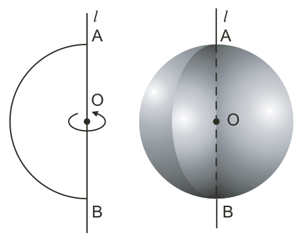
Khi quay nửa hình tròn tâm O, bán kính R một vòng quanh đường kính AB cố định thì được một hình cầu.

- Nửa đường tròn trong phép quay nói trên tạo thành một mặt cầu.

- Điểm O được gọi tâm, R là bán kính của hình cầu hay mặt cầu đó.

2. Cắt hình cầu bởi một mặt phẳng

Khi cắt hình cầu bởi một mặt phẳng ta được một hình tròn.

Ví dụ 1. Mặt phẳng (P) cắt hình cầu tâm O, bán kính R ta được hình tròn như hình vẽ.

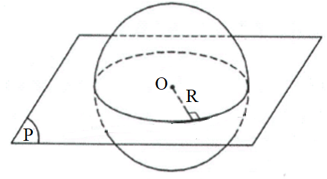
Khi cắt mặt cầu bán kính R bởi một mặt phẳng ta được một đường tròn:

- Đường tròn đó có bán kính R nếu mặt phẳng đi qua tâm (gọi là đường tròn lớn).

- Đường tròn đó có bán kính bé hơn R nếu mặt phẳng không đi qua tâm.

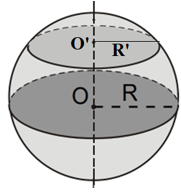
Ví dụ 2. Khi cắt mặt cầu tâm O bán kính R bởi một mặt phẳng ta được:

- Đường tròn tâm O bán kính R: mặt phẳng đi qua tâm.

- Đường tròn tâm O’ bán kính R’: mặt phẳng không đi qua tâm.

Ta có hình vẽ:

3. Diện tích và thể tích của hình cầu

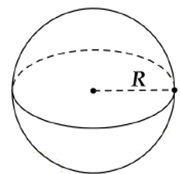
Ví dụ 3. Một hình cầu có thể tích bằng 972π cm³. Tính diện tích của mặt cầu đó.

Lời giải:

Bán kính của mặt cầu đó là:

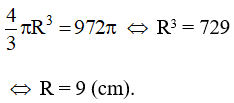
Diện tích của mặt cầu đó là:

S = 4πR² = 4π . 9² = 324π (cm²)

Vậy diện tích của mặt cầu đó là 324π cm².

B. Bài tập tự luyện

Bài 1. Hai hình cầu có hiệu các bán kính bằng 3 cm và hiệu các thể tích bằng 1332π cm³. Tính hiệu các diện tích của hai mặt cầu.

Lời giải:

Gọi bán kính của hình cầu lớn là R và bán kính của hình cầu nhỏ là r.

Ta có R – r = 3 hay R = r + 3.

Nên:

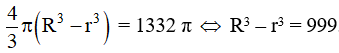
Do đó (r + 3)³ – r³ = 999$\iff$ r² + 3r – 108 = 0.

Giải ra được r₁ = –12 (loại), r₂ = 9 (chọn).

Do đó bán kính hình cầu nhỏ là 9 cm, bán kính hình cầu lớn là 12 cm.

Diện tích mặt cầu lớn là:

S₁ = 4πR² = 4π . 12² = 576π (cm²).

Diện tích mặt cầu nhỏ là:

S₂ = 4πr² = 4π . 9² = 324π (cm²).

Hiệu diện tích hai mặt cầu là:

S = S₁ – S₂ = 576π – 324π = 252π (cm²)

Vậy hiệu diện tích hai mặt cầu là 252π cm².

Bài 2. Một hình cầu có bán kính bằng bán kính đáy của một hình nón. Biết đường sinh của hình nón bằng 12 cm và diện tích xung quanh của hình nón bằng diện tích mặt cầu. Tính thể tích hình cầu.

Lời giải:

Gọi bán kính hình cầu cũng như bán kính đáy hình nón là R.

Diện tích xung quanh hình nón là: πRl = 12πR.

Diện tích mặt cầu là: 4πR².

Vì diện tích xung quanh hình nón bằng diện tích mặt cầu nên:

12πR = 4πR² $\Rightarrow$ R = 3 (cm).

Thể tích hình cầu là: $V=\frac{4}{3}\pi R^3$$=\frac{4}{3}\pi .3^3=36\pi$ (cm³).

Vậy thể tích hình cầu là 36π cm³.

Bài 3. Cho một hình cầu nội tiếp một hình trụ. Chứng minh rằng:

a) Thể tích hình cầu bằng $\frac{2}{3}$ thể tích hình trụ;

b) Diện tích mặt cầu bằng $\frac{2}{3}$ diện tích toàn phần hình trụ.

Lời giải:

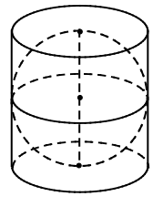
Gọi bán kính hình cầu là R thì bán kính đáy hình trụ là R và chiều cao hình trụ là 2R.

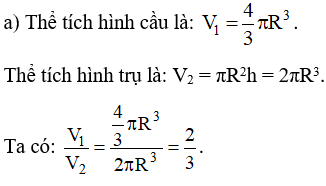
Vậy thể tích hình cầu bằng $\frac{2}{3}$ thể tích hình trụ.

b) Diện tích mặt cầu là: S₁ = 4πR².

Diện tích hình trụ là: S₂ = 2πR(h + R) = 2πR(2R + R) = 6πR².

Ta có: $\frac{S_1}{S_2}=\frac{4\pi R^2}{6\pi R^2}=\frac{2}{3}$.

Vậy diện tích mặt cầu bằng $\frac{2}{3}$ diện tích toàn phần hình trụ.

Xem thêm các bài tổng hợp lý thuyết Toán lớp 9 đầy đủ, chi tiết khác:

Lý thuyết Diện tích hình tròn, hình quạt tròn

Lý thuyết Ôn tập chương 3

Lý thuyết Hình trụ - Diện tích xung quanh và thể tích của hình trụ

Lý thuyết Hình nón – Hình nón cụt. Diện tích xung quanh và thể tích của hình nón, hình nón cụt

Lý thuyết Ôn tập chương 4