Lý thuyết Độ dài đường tròn, cung tròn (mới 2024 + Bài Tập) - Toán 9
Lý thuyết Độ dài đường tròn, cung tròn lớp 9 gồm lý thuyết chi tiết, ngắn gọn và bài tập tự luyện có lời giải chi tiết sẽ giúp học sinh nắm vững kiến thức trọng tâm Toán 9 Bài 9: Độ dài đường tròn, cung tròn.
Lý thuyết Toán 9 Bài 9: Độ dài đường tròn, cung tròn
Bài giảng Toán 9 Bài 9: Độ dài đường tròn, cung tròn
A. Lý thuyết
1. Công thức tính độ dài đường tròn
“Độ dài đường tròn” hay còn được gọi là “chu vi đường tròn” được kí hiệu là C.
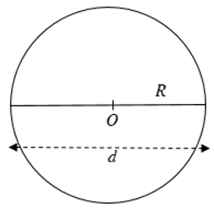
Công thức tính chu vi hình tròn: C = 2πR hoặc C = πd.
Trong đó: C là độ dài đường tròn;
R là bán kính đường tròn;
d là đường kính của đường tròn;
π (đọc là “pi”) là kí hiệu của một số vô tỉ mà giá trị gần đúng thường được lấy là π ≈ 3,14.
Ví dụ 1. Cho đường tròn có bán kính 5 cm. Tính độ dài đường tròn đó?
Lời giải:
Độ dài đường tròn là:
C = 2πR = 2π . 5 = 10π (cm).
Vậy đường tròn có bán kính R = 5 cm có độ dài đường tròn là 10π cm.
2. Công thức tính độ dài cung tròn
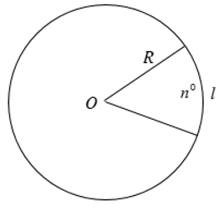

Ví dụ 2. Cho đường tròn có bán kính 4cm. Tính độ dài cung tròn 120o.
Lời giải:
Độ dài cung tròn 120o là:
(cm)
Vậy độ dài cung tròn 120o của đường tròn (O; 4cm) là cm.
B. Bài tập tự luyện
Bài 1. Cho đường tròn (O) bán kính OA. Từ trung điểm M của OA vẽ dây BC vuông góc OA. Biết độ dài đường tròn (O) là 4π (cm). Tính:
a) Bán kính đường tròn (O).
b) Độ dài hai cung BC của đường tròn.
Lời giải:
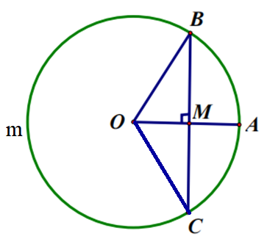
a) Độ dài bán kính đường tròn (O) là:
![]()
b) Áp dụng định lý Py – ta – go vào ∆BOM vuông tại M, ta có:
BM2 + OM2 = OB2
![]()
∆BOM vuông tại M nên = 60o.
∆OBC cân tại O (vì OB = OC) có OM là đường cao nên OM cũng là đường phân giác.
Suy ra
Đặt cung lớn BC là .
Số đo của cung lớn BC là:
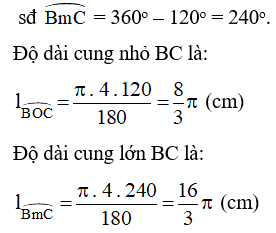
Vậy độ dài cung nhỏ và cung lớn BC lần lượt là 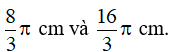
Bài 2. Tam giác ABC có AB = AC = 3 cm, . Tính độ dài đường tròn ngoại tiếp ∆ABC.
Lời giải:
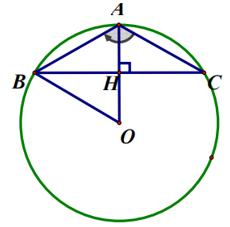
Ta có AB = AC nên A là điểm nằm chính giữa cung BC.
Suy ra:
Do đó ∆ABH là nửa tam giác đều.
Nên AB = BO = 3 (cm).
Vậy độ dài đường tròn ngoại tiếp ∆ABC là: C = 2πR = 6π (cm).
Bài 3. Một tam giác đều và một hình vuông có cùng chu vi là 72 cm. Hỏi độ dài đường tròn ngoại tiếp hình nào lớn hơn? Lớn hơn bao nhiêu?
Lời giải:
* Xét tam giác ABC đều ngoại tiếp đường tròn (O) có chu vi 72 cm.
Kẻ AH là đường trung trực của ∆ABC tại H.
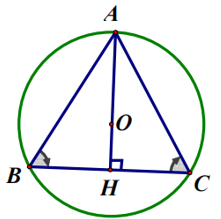
Độ dài cạnh của tam giác đều: 72 : 3 = 24 (cm)
Áp dụng định lý Py – ta – go vào ∆ABH vuông tại H, ta có:
AH2 + BH2 = AB2
![]()
Đường tròn (O) ngoại tiếp ∆ABC nên AH là đường trung trực của ∆ABC.
Mà ∆ABC đều nên AH cũng là đường trung tuyến.
Suy ra O cũng là trọng tâm của ∆ABC.
Do đó OA = AH = = R.
Do đó độ dài đường tròn ngoại tiếp tam giác đều là:
C = 2πR = π (cm).
* Xét hình vuông MNPQ ngoại tiếp đường tròn (O’) có chu vi 72 cm.
Nối N với Q.
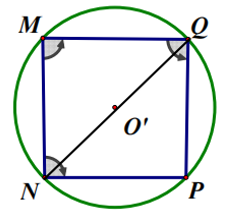
Độ dài các cạnh của hình vuông là: 72 : 4 = 18 (cm).
Áp dụng định lý Py – ta – go vào ∆NPQ vuông tại P, ta có:
NP2 + PQ2 = NQ2
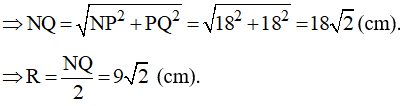
Do đó độ dài đường tròn ngoại tiếp hình vuông là:
![]()
Vậy độ dài đường tròn ngoại tiếp tam giác đều lớn hơn đường tròn ngoại tiếp hình vuông và lớn hơn:
![]()
Xem thêm các bài tổng hợp lý thuyết Toán lớp 9 đầy đủ, chi tiết khác:
Lý thuyết Đường tròn ngoại tiếp. Đường tròn nội tiếp
Xem thêm các chương trình khác:
- Giải sgk Hóa học 9 (sách mới) | Giải bài tập Hóa 9
- Giải sbt Hóa học 9
- Giải vở bài tập Hóa học 9
- Lý thuyết Hóa học 9
- Các dạng bài tập Hóa học lớp 9
- Tóm tắt tác phẩm Ngữ văn 9 (sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Soạn văn 9 (hay nhất) | Để học tốt Ngữ văn 9 (sách mới)
- Soạn văn 9 (ngắn nhất)
- Văn mẫu 9 (sách mới) | Để học tốt Ngữ văn 9 Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Tác giả - tác phẩm Ngữ văn 9 (sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Giải sgk Tiếng Anh 9 (thí điểm)
- Giải sgk Tiếng Anh 9 (sách mới) | Để học tốt Tiếng Anh 9
- Giải sbt Tiếng Anh 9
- Giải sbt Tiếng Anh 9 (thí điểm)
- Giải sgk Sinh học 9 (sách mới) | Giải bài tập Sinh học 9
- Giải vở bài tập Sinh học 9
- Lý thuyết Sinh học 9
- Giải sbt Sinh học 9
- Giải sgk Vật Lí 9 (sách mới) | Giải bài tập Vật lí 9
- Giải sbt Vật Lí 9
- Lý thuyết Vật Lí 9
- Các dạng bài tập Vật lí lớp 9
- Giải vở bài tập Vật lí 9
- Giải sgk Địa Lí 9 (sách mới) | Giải bài tập Địa lí 9
- Lý thuyết Địa Lí 9
- Giải Tập bản đồ Địa Lí 9
- Giải sgk Tin học 9 (sách mới) | Giải bài tập Tin học 9
- Lý thuyết Tin học 9
- Lý thuyết Giáo dục công dân 9
- Giải vở bài tập Lịch sử 9
- Giải Tập bản đồ Lịch sử 9
- Lý thuyết Lịch sử 9
- Lý thuyết Công nghệ 9
