Nội dung bài viết

    Xem thêm

    Lý thuyết Hình nón – Hình nón cụt. Diện tích xung quanh và thể tích của hình nón, hình nón cụt (mới 2024 + Bài Tập) - Toán 9

    Lý thuyết Hình nón – Hình nón cụt. Diện tích xung quanh và thể tích của hình nón, hình nón cụt lớp 9 gồm lý thuyết chi tiết, ngắn gọn và bài tập tự luyện có lời giải chi tiết sẽ giúp học sinh nắm vững kiến thức trọng tâm Toán 9 Bài 2: Hình nón – Hình nón cụt. Diện tích xung quanh và thể tích của hình nón, hình nón cụt.

    1 2,760 21/12/2023
    Tải về
    Trang trước
    Chia sẻ
    Trang sau  

    Lý thuyết Toán 9 Bài 2: Hình nón – Hình nón cụt. Diện tích xung quanh và thể tích của hình nón, hình nón cụt

    Bài giảng Toán 9 Bài 2: Hình nón – Hình nón cụt. Diện tích xung quanh và thể tích của hình nón, hình nón cụt

    A. Lý thuyết

    1. Hình nón

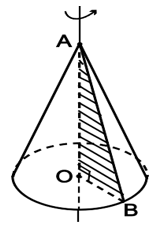
    Khi quay tam giác vuông AOC một vòng quanh cạnh OA cố định thì được một hình nón.

    - Điểm A được gọi đỉnh của hình nón.

    - Hình tròn (O) được gọi là đáy của hình nón.

    - Mỗi vị trí của AC được gọi là một đường sinh của hình nón.

    - Đoạn AO được gọi là đường cao của hình nón.

    Lý thuyết Hình nón – Hình nón cụt. Diện tích xung quanh và thể tích của hình nón, hình nón cụt chi tiết – Toán lớp 9 (ảnh 1)

    2. Diện tích và thể tích của hình nón

    Đặt AC = l; l là đường sinh.

    Cho hình nón có bán kính đáy R và đường sinh l, chiều cao h.

    - Diện tích xung quanh: Sxq = πRl.

    - Diện tích toàn phần: Stp = πRl + πR2.

    - Thể tích: V=13πR2h.

    Ví dụ 1. Một hình nón có đường cao bằng 24 cm và thể tích bằng 800π cm3. Tính diện tích toàn phần của hình nón này.

    Lời giải:

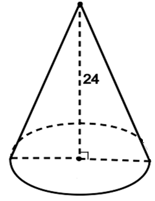
    Lý thuyết Hình nón – Hình nón cụt. Diện tích xung quanh và thể tích của hình nón, hình nón cụt chi tiết – Toán lớp 9 (ảnh 1)

    Gọi R là bán kính và h là chiều cao của hình nón.

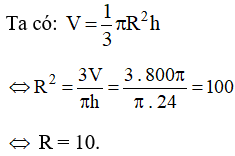
    Lý thuyết Hình nón – Hình nón cụt. Diện tích xung quanh và thể tích của hình nón, hình nón cụt chi tiết – Toán lớp 9 (ảnh 1)

    Do đó bán kính của hình nón là 10 cm.

    Đường sinh của hình nón là:

    SB2=SO2+OB2=242+102=26cm

    Diện tích toàn phần của hình nón là:

    Stp = πR(l + R) = π . 10 (26 + 10) = 360π (cm2).

    3. Hình nón cụt

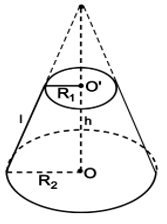
    Khi cắt hình nón bởi một mặt phẳng song song với đáy thì phần hình nón nằm giữa mặt phẳng nói trên và mặt phẳng đáy được gọi là một hình nón cụt.

    - Hai hình tròn (O) và (O') được gọi là hai đáy.

    - Đoạn OO' được gọi là trục. Độ dài OO' là chiều cao.

    - Đoạn AC được gọi là đường sinh.

    Lý thuyết Hình nón – Hình nón cụt. Diện tích xung quanh và thể tích của hình nón, hình nón cụt chi tiết – Toán lớp 9 (ảnh 1)

    4. Diện tích và thể tích hình nón cụt

    Cho hình nón cụt có các bán kính đáy R và r, chiều cao h, đường sinh l.

    - Diện tích xung quanh: Sxq = π (R + r) l.

    - Thể tích: V=13πh(R2+Rr+r2).

    Ví dụ 2. Một hình nón đỉnh S có bán kính đáy bằng 9 cm và chiều cao SO = 21,6 cm. Cắt hình nón bởi một mặt phẳng song song với đáy tạo ra một hình nón cụt có chiều cao 12 cm. Tính diện tích xung quanh của hình nón cụt.

    Lời giải:

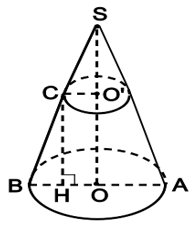
    Lý thuyết Hình nón – Hình nón cụt. Diện tích xung quanh và thể tích của hình nón, hình nón cụt chi tiết – Toán lớp 9 (ảnh 1)

    Xét mặt cắt qua trục của hình nón là ∆SAB cân tại S.

    Trong mặt phẳng SAB có O’C // OB.

    Theo định lý Ta – lét ta có O'COB=SO'SO.

    Do đó O'C9=9,621,6⇒ O’C = 4 (cm).

    Trong mặt phẳng SAB vẽ CH⊥AB, ta được:

    CH = OO’ = 12 cm, BH = 9 – 4 = 5 (cm).

    Suy ra BC = BH2+CH2=122+52=13 (cm)

    Diện tích xung quanh của hình nón cụt là:

    Sxq = π(R1 + R2)l = π(9 + 4) . 13 = 169π (cm2)

    Vậy diện tích xung quanh của hình nón cụt là 169π cm2.

    B. Bài tập tự luyện

    Bài 1. Mặt cắt chứa trục của một hình nón là một tam giác đều có diện tích 93cm2. Tính thể tích của hình nón đó.

    Lời giải:

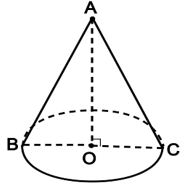
    Lý thuyết Hình nón – Hình nón cụt. Diện tích xung quanh và thể tích của hình nón, hình nón cụt chi tiết – Toán lớp 9 (ảnh 1)

    Gọi mặt cắt là tam giác đều ABC, đáy của hình nón có tâm là O.

    Ta đặt AB = AC = BC = a thì bán kính đáy hình nón là R=a2 và chiều cao của hình nón là h=a32.

    Vì diện tích của tam giác đều là 93 cm2 nên ta có:

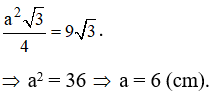
    Lý thuyết Hình nón – Hình nón cụt. Diện tích xung quanh và thể tích của hình nón, hình nón cụt chi tiết – Toán lớp 9 (ảnh 1)

    Do đó bán kính đáy là R = 3 cm và chiều cao hình nón là:

    h=632=33(cm)

    Thể tích của hình nón là:

    V=13πR2h=13π  .  32 .  33=93π (cm3)

    Vậy thể tích của hình nón là: 93 cm3.

    Bài 2. Một hình nón cụt có các bán kính đáy là 21 cm và 49 cm. Biết diện tích xung quanh của nó là 3710π cm2. Tính thể tích của hình nón cụt.

    Lời giải:

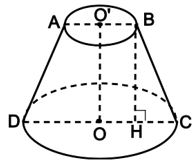
    Lý thuyết Hình nón – Hình nón cụt. Diện tích xung quanh và thể tích của hình nón, hình nón cụt chi tiết – Toán lớp 9 (ảnh 1)

    Gọi mặt cắt chứa trục của hình nón cụt là hình thang cân ABCD.

    Trong mặt phẳng này vẽ BH⊥CD.

    Ta đặt O’B= R1, OC = R2, OO’ = h và BC = 1.

    Ta có: BH = OO’ = h; HC = R2 – R1 = 49 – 21 = 28 (cm).

    Vì diện tích xung quanh của hình nón cụt là 3710π cm2 nên:

    π(R1 +R2)l = 3710π

    Suy ra: l=3710ππ(21+49)=53 (cm)

    Xét ∆BHC vuông tại H, ta có:

    BH=BC2−HC2=532−282=45cm

    Thể tích của hình nón cụt là:

    V=13πh(R12+R22+R1R2)=13π  .  45(212+492+21  .  49)=58  065 π cm3

    Vậy thể tích của hình nón cụt là 58 065π cm3.

    Bài 3. Một chao đèn có dạng mặt xung quanh của một hình nón cụt. Các bán kính đáy lần lượt là R1 = 5 cm, R2 = 13 cm. Biết diện tích xung quanh của chao đèn là 306π cm2. Tính chiều cao của chao đèn.

    Lời giải:

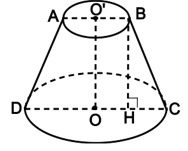
    Lý thuyết Hình nón – Hình nón cụt. Diện tích xung quanh và thể tích của hình nón, hình nón cụt chi tiết – Toán lớp 9 (ảnh 1)

    Gọi mặt cắt chứa trục của chao đèn là hình thang cân ABCD.

    Chiều cao OO’ = h và đường sinh BC = l.

    Vì diện tích xung quanh của chao đèn là 306π cm2 nên ta có:

    π(R1 + R2)l = 306 π

    ⇒ π(5 + 13)l = 306 π

    ⇒ l = 17 (cm)

    Trong mặt phẳng ABCD ta vẽ BH⊥CD.

    Ta có BH = OO’ = h; OH = O’B = R1.

    Do đó HC = R2 – R1 = 8 (cm).

    Xét ∆BHC vuông tại H, ta có:

    BH=BC2−HC2=172−82=15 (cm)

    Vậy chiều cao của chao đèn là 15 cm.

    Xem thêm các bài tổng hợp lý thuyết Toán lớp 9 đầy đủ, chi tiết khác:

    Lý thuyết Diện tích hình tròn, hình quạt tròn

    Lý thuyết Ôn tập chương 3

    Lý thuyết Hình trụ - Diện tích xung quanh và thể tích của hình trụ

    Lý thuyết Hình cầu. Diện tích mặt cầu và thể tích hình cầu

    Lý thuyết Ôn tập chương 4

    Tham khảo các loạt bài Toán 9 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 2,760 21/12/2023
    Tải về
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: