Lý thuyết Góc có đỉnh ở bên trong đường tròn. Góc có đỉnh ở bên ngoài đường tròn (mới 2024 + Bài Tập) - Toán 9
Lý thuyết Góc có đỉnh ở bên trong đường tròn. Góc có đỉnh ở bên ngoài đường tròn lớp 9 gồm lý thuyết chi tiết, ngắn gọn và bài tập tự luyện có lời giải chi tiết sẽ giúp học sinh nắm vững kiến thức trọng tâm Toán 9 Bài 5: Góc có đỉnh ở bên trong đường tròn. Góc có đỉnh ở bên ngoài đường tròn.
Lý thuyết Toán 9 Bài 5: Góc có đỉnh ở bên trong đường tròn. Góc có đỉnh ở bên ngoài đường tròn
Bài giảng Toán 9 Bài 5: Góc có đỉnh ở bên trong đường tròn. Góc có đỉnh ở bên ngoài đường tròn
A. Lý thuyết
1. Góc có đỉnh ở bên trong đường tròn
- Góc có đỉnh nằm bên trong đường tròn được gọi là góc có đỉnh ở bên trong đường tròn.
- Định lí: Số đo của góc có đỉnh ở bên trong đường tròn bằng nửa tổng số đo hai cung bị chắn.
Ví dụ 1. Cho đường tròn (O) có hai dây AB và CD cắt nhau tại E (điểm E nằm bên trong đường tròn) như hình vẽ.
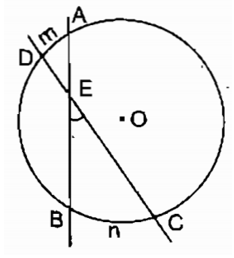
Trong hình vẽ trên, là góc có đỉnh nằm ở bên trong đường tròn chắn hai cung là .
Do đó, 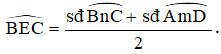
2. Góc có đỉnh nằm bên ngoài đường tròn
- Góc có đỉnh ở bên ngoài đường tròn là góc có đỉnh nằm ngoài đường tròn và các cạnh đều có điểm chung với đường tròn.
- Định lí: Số đo của góc có đỉnh ở bên ngoài đường tròn bằng nửa hiệu số đo hai cung bị chắn.
Ví dụ 2. Cho đường tròn (O) có hai dây AB và CD cắt nhau tại E (điểm E nằm bên ngoài đường tròn) như hình vẽ.
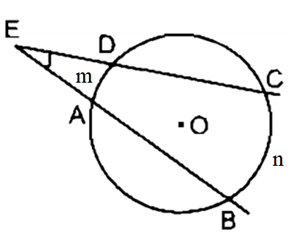
Trong hình vẽ trên, là góc có đỉnh nằm ở bên ngoài đường tròn chắn hai cung là .
Do đó, 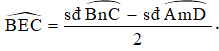
B. Bài tập tự luyện
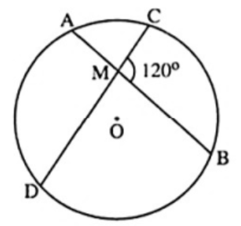
Bài 1. Cho đường tròn đường tròn (O) có hai dây AB và CD cắt nhau tại M như hình vẽ. Tính số đo của cung BD, biết .
Lời giải:

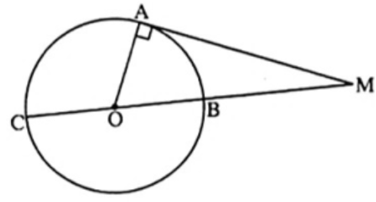
Bài 2. Cho đường tròn đường tròn (O) đường kính BC. Lấy điểm A nằm trên đường tròn, vẽ tiếp tuyến AM (A là tiếp điểm). Tính , biết số đo cung AC là 120o.
Lời giải:
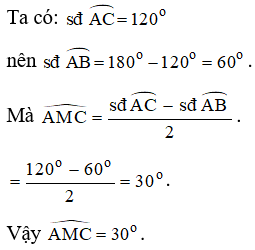
Bài 3. Từ điểm A nằm bên ngoài đường tròn (O) kẻ tiếp tuyến AB và cát tuyến ACD. Vẽ dây BM vuông góc với tia phân giác góc BAC tại H cắt CD tại E. Chứng minh BM là đường phân giác góc CBD.
Lời giải:
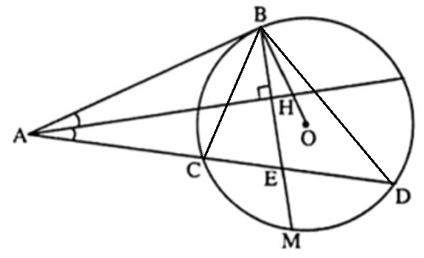
∆ABE có AH là đường phân giác đồng thời là đường cao nên ∆ABE cân tại đỉnh A.

Xem thêm các bài tổng hợp lý thuyết Toán lớp 9 đầy đủ, chi tiết khác:
Lý thuyết Đường tròn ngoại tiếp. Đường tròn nội tiếp
Xem thêm các chương trình khác:
- Giải sgk Hóa học 9 (sách mới) | Giải bài tập Hóa 9
- Giải sbt Hóa học 9
- Giải vở bài tập Hóa học 9
- Lý thuyết Hóa học 9
- Các dạng bài tập Hóa học lớp 9
- Tóm tắt tác phẩm Ngữ văn 9 (sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Soạn văn 9 (hay nhất) | Để học tốt Ngữ văn 9 (sách mới)
- Soạn văn 9 (ngắn nhất)
- Văn mẫu 9 (sách mới) | Để học tốt Ngữ văn 9 Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Tác giả - tác phẩm Ngữ văn 9 (sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Giải sgk Tiếng Anh 9 (thí điểm)
- Giải sgk Tiếng Anh 9 (sách mới) | Để học tốt Tiếng Anh 9
- Giải sbt Tiếng Anh 9
- Giải sbt Tiếng Anh 9 (thí điểm)
- Giải sgk Sinh học 9 (sách mới) | Giải bài tập Sinh học 9
- Giải vở bài tập Sinh học 9
- Lý thuyết Sinh học 9
- Giải sbt Sinh học 9
- Giải sgk Vật Lí 9 (sách mới) | Giải bài tập Vật lí 9
- Giải sbt Vật Lí 9
- Lý thuyết Vật Lí 9
- Các dạng bài tập Vật lí lớp 9
- Giải vở bài tập Vật lí 9
- Giải sgk Địa Lí 9 (sách mới) | Giải bài tập Địa lí 9
- Lý thuyết Địa Lí 9
- Giải Tập bản đồ Địa Lí 9
- Giải sgk Tin học 9 (sách mới) | Giải bài tập Tin học 9
- Lý thuyết Tin học 9
- Lý thuyết Giáo dục công dân 9
- Giải vở bài tập Lịch sử 9
- Giải Tập bản đồ Lịch sử 9
- Lý thuyết Lịch sử 9
- Lý thuyết Công nghệ 9
