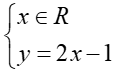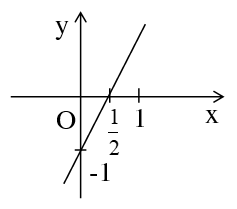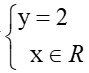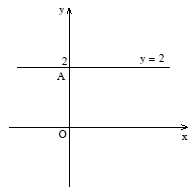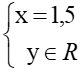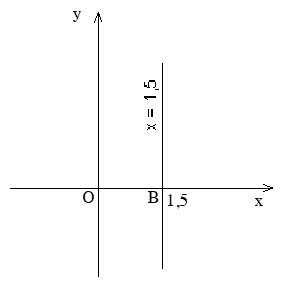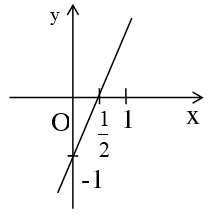Giáo án Phương trình bậc nhất hai ẩn mới nhất - Toán 9
Với Giáo án Phương trình bậc nhất hai ẩn mới nhất Toán lớp 9 được biên soạn bám sát sách Toán 9 giúp Thầy/ Cô biên soạn giáo án dễ dàng hơn.
Giáo án Toán 9 Bài 1: Phương trình bậc nhất hai ẩn
I. Mục tiêu
Qua bài này giúp HS:
1. Kiến thức
- Phát biều được khái niệm phương trình bậc nhất hai ẩn và nghiệm của nó. Nêu được tập nghiệm của một phương trình bậc nhất hai ẩn và biểu diễn hình học của nó.
- Tìm được công thức nghiệm tổng quát và vẽ được đường biểu diễn tập nghiệm của một phương trình bậc nhất hai ẩn.
- Phát hiện được công thức nghiệm tổng quát của phương trình bậc nhất hai ẩn.
2. Kỹ năng
- Tính được số gà, chó trong bài toán cổ.
- Biểu diễn chính xác nghiệm của phương trình bậc nhất hai ẩn trên mặt phẳng tọa độ.
- Viết được nghiệm tổng quát của phương trình bậc nhất hai ẩn.
3. Thái độ
- Nghiêm túc và hứng thú học tập.
- Yêu thích môn học.
4. Định hướng năng lực
- Năng lực tính toán
- Năng lực giải quyết vấn đề
- Năng lực hợp tác.
- Năng lực ngôn ngữ
- Năng lực giao tiếp.
- Năng lực tự học.
Phẩm chất: Tự lập, tự tin.
II. Chuẩn bị
- Gv : Thước thẳng, bảng phụ, phấn mầu.
- Hs : Thước thẳng, ôn tập kiến thức.
III. Tiến trình dạy học
1. Ổn định (1 phút)
2. Kiểm tra bài cũ (Kết hợp trong giờ dạy)
3. Bài mới
| Giáo viên | Học sinh | Nội dung ghi bài |
|---|---|---|
|
A - Hoạt động khởi động (2 phút) - Mục tiêu: HS gọi được ẩn phụ và biểu diễn các phương trình theo dữ kiện đề bài cho, phát hiện được ví dụ về phương trình bậc nhất hai ẩn. - Phương pháp: Nêu vấn đề, thuyết trình, vấn đáp. |
||
|
Chúng ta đã được học về phương trình bậc nhất một ẩn. Trong thực tế còn có các tình huống dẫn đến phương trình có nhiều hơn một ẩn, như phương trình bậc nhất hai ẩn. Ví dụ trong bài toán cổ “Vừa gà vừa chó”. Nếu ta ký hiệu số gà là x, số chó là y thì giả thiết có 36 con vừa gà vừa chó suy ra x + y = 36. giả thiết có 100 chân cả gà và chó suy ra 2x + 4y = 100. Đó là các ví dụ về phương trình bậc nhất hai ẩn. Trong chương chúng ta sẽ học các nội dung như: - Phương trình và hệ phương trình bậc nhất hai ẩn. - Các cách giải hệ phương trình. - Giải bài toán bằng cách lập hệ phương trình. |
||
|
B - Hoạt động hình thành kiến thức – 36 phút. Khái niệm về phương trình bậc nhất hai ẩn - Mục tiêu: Hs nắm được khái niệm về phương trình bậc nhất hai ẩn và tập nghiệm của pt bậc nhất hai ẩn, biết cách biểu diễn tập nghiệm bằng hình vẽ - Phương pháp: Nêu vấn đề, thuyết trình, vấn đáp. |
||
|
*Mục tiêu: *Giao nhiệm vụ: Làm các bài tập ?1,?2 và các ví dụ *Hình thức tổ chức: Hoạt động cá nhân *Tiến hành hoạt động: Ta thấy x+y=36; 2x+4y=100 là các ví dụ về phương trình bậc nhất hai ẩn. - gv giới thiệu định nghĩa (Như phần Nội dung) Cách nói khác: Là hệ thức có dạng ax + by = c trong đó a; b; c là các hệ số a và b không đồng thời bằng 0 NV1: Hãy lấy ví dụ về phương trình bậc nhất hai ẩn NV2: Củng cố: Trong các phương trình sau, pt nào là pt bậc nhất hai ẩn? xác định các hệ số a,b,c tương ứng. a) 4x-0,5y=0 b) 3x2+x=5 c) 0x-3y=0 d) 2x-0y=0 e) 0x+0y=2 f) 2x+y-z=3 Gv: Xét phương trình x+y=36. Ta thấy x=2; y=34 thì giá trị của vế trái bằng vế phải. Ta nói cặp số x=2; y=34 hay cặp số (2;34) là một nghiệm của phương trình Gv giới thiệu nghiệm của pt bậc nhất hai ẩn. NV3: ? Có kết luận gì về số nghiệm của pt bậc nhất hai ẩn Ví dụ 2: Chứng tỏ cặp số (3;5) là một nghiệm của phương trình 2x – y = 1 Gv nêu chú ý sgk Yêu cầu hsinh trả lời ?1; ?2 Hãy nêu nhận xét về số nghiệm của phương trình 2x – y = 1 Gv đưa ra công thức ngh TQ của ?2 |
Học sinh chú ý lắng nghe, ghi nhớ. Hs nhắc lại đ/n Ví dụ: Học sinh tự nêu. +, a; c; d là các pt bậc nhất 2 ẩn a) a = 4; b = -0,5; c= 0 c) a = 0; b = -3; c= 0. d) a = 2; b = 0; c= 0. +, b; e; f không là pt bậc nhất 2 ẩn hs ghi nhớ PT bậc nhất 2 ẩn có vô số nghiệm Học sinh phát biểu nhận xét. |
1. Khái niệm về phương trình bậc nhất hai ẩn. + Tổng quát: Phương trình bậc nhất hai ẩn x, y là hệ thức có dạng: ax + by = c (1) Trong đó a, b, c là các số đã biết và a#0 hoặc b#0 Ví dụ: 3x + 2y = 6 0x-3y=7 x+y=-3 + x = x0; y = y0 thỏa mãn ax0 + by0 = 0 suy ra (x0; y0) là nghiệm của pt bậc nhất hai ẩn ax + by = 0 + Pt bậc nhất hai ẩn có vô số nghiệm. Mỗi nghiệm (x0; y0) được biểu diễn bởi 1 điểm trên mặt phẳng tọa độ. ?1: Cặp số (1;1) cũng là một nghiệm của phương trình 2x–y=1 tương tự (0,5; 0) cũng là nghiệm của phương trình b) Các nghiệm khác như (0; - 1) ; (2;3) ……….. Phương trình 2x – y = 1 có vô số nghiệm mỗi nghiệm là một cặp số |
|
Tập nghiệm của phương trình bậc nhất hai ẩn - Mục tiêu: HS phát hiện được trong mặt phẳng tọa độ, tập hợp các điểm biểu diễn nghiệm của phương trình bậc nhất hai ẩn là 1 đường thẳng. - Phương pháp: Nêu vấn đề, thuyết trình, vấn đáp. |
||
|
(Hoạt động cá nhân) Ta đã biết phương trình bậc nhất hai ẩn có vô số nghiệm, vậy làm thế nào để biểu diễn nghiệm của phương trình? Gv giới thiệu cách biểu diễn nghiệm của pt 2x-y=1 Trong mặt phẳng toạ độ Oxy tập hợp các nghiệm được biểu diễn các nghiệm của phương trình (2) là đường thẳng y=2x-1 ( gv treo bảng phụ vẽ sẵn hình 1 ) Xét PT: 0x +2y = 4 (4) +Hãy chỉ ra vài nghiệm PT(4)? Vậy nghiệm TQ của (4)? +Yêu cầu HS biểu diễn nghiệm TQ của PT (4) Xét PT:4x+0y=6 (5) +Hãy chỉ ra vài nghiệm PT(5)? Vậy nghiệm TQ của (5)? +Yêu cầu HS biểu diễn nghiệm TQ của PT (5) Cho các phương trình sau: 0x + 2y = 0 0x + y = 0 4x + 0y = 6 x + 0y = 0 (Hoạt động nhóm) - Nêu nghiệm tổng quát các phương trình - Đường thẳng biểu diễn tập hợp nghiệm của mỗi phương trình là đường thẳng nào? Treo bảng phụ ghi phần tổng quát SGK |
Học sinh chú ý lắng nghe Học sinh thực hiện câu hỏi 3? Một em lên bảng thực hiện . Học sinh lên bảng vẽ đường thẳng y = 2x – 1 trên hệ trục toạ độ. HS trả lời HS trả lời Học sinh hoạt động nhóm Nửa lớp làm câu a,d a) y = 0; x ∈ R d) X = 0; Y ∈ R Nửa còn lại làm câu b,c b) x = c) x = 0; y ∈ 0 Học sinh treo kết quả hoạt động nhóm lên bảng. |
2) Tập nghiệm của phương trình bậc nhất hai ẩn. +Xét phương trình : 2x – y = 1 CT NTQ: (x; 2x-1) hoặc viết - Tập nghiệm S={x; 2x-1/x ∈ R} - Trên mặt phẳng tọa độ là đường thẳng y=2x-1 + Xét phương trình 0x+2y =4 Ta nhận thấy phương trình có nghiệm với mọi x và y=2 nên ta có nghiệm tổng quát của phương trình là (x; 2 ) hay Đồ thị + Xét phương trình 4x+0y =6 Ta nhận thấy phương trình có nghiệm với mọi x và x=1,5 nên ta có nghiệm tổng quát của phương trình là (1,5; y) hay Đồ thị: Tổng quát: ( SGK) |
|
C - Hoạt động luyện tập – 5 phút Mục tiêu: Củng cố lại kiến thức đã học trong bài PP: Vấn đáp, thuyết trình. |
||
|
Phương trình bậc nhất hai ẩn là gì? Nghiệm của phương trình bậc nhất hai ẩn? Có bao nhiêu nghiệm số? Cho học sinh làm bài 2a; sgk |
Một học sinh trả lời Học sinh khác nhận xét bài làm của bạn Một học sinh vẽ đường thẳng |
|
|
D – Tìm tòi, mở rộng – 1 phút - Mục tiêu: - HS chủ động làm các bài tập về nhà để củng cố kiến thức đã học. - HS chuẩn bị bài mới giúp tiếp thu tri thức sẽ học trong buổi sau. - Kĩ thuật sử dụng: Kĩ thuật viết tích cực |
||
|
- Học bài - Làm BTVN bài 1,2,3 SGK, SBT. Đọc mục có thể em chưa biết. trang 8 |
||
Xem thêm các bài Giáo án Toán lớp 9 hay, chi tiết khác:
Giáo án Hệ hai phương trình bậc nhất hai ẩn
Giáo án Giải hệ phương trình bằng phương pháp thế
Giáo án Giải hệ phương trình bằng phương pháp cộng đại số
Xem thêm các chương trình khác:
- Giải sgk Hóa học 9 (sách mới) | Giải bài tập Hóa 9
- Giải sbt Hóa học 9
- Giải vở bài tập Hóa học 9
- Lý thuyết Hóa học 9
- Các dạng bài tập Hóa học lớp 9
- Tóm tắt tác phẩm Ngữ văn 9 (sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Soạn văn 9 (hay nhất) | Để học tốt Ngữ văn 9 (sách mới)
- Soạn văn 9 (ngắn nhất)
- Văn mẫu 9 (sách mới) | Để học tốt Ngữ văn 9 Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Tác giả - tác phẩm Ngữ văn 9 (sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Giải sgk Tiếng Anh 9 (thí điểm)
- Giải sgk Tiếng Anh 9 (sách mới) | Để học tốt Tiếng Anh 9
- Giải sbt Tiếng Anh 9
- Giải sbt Tiếng Anh 9 (thí điểm)
- Giải sgk Sinh học 9 (sách mới) | Giải bài tập Sinh học 9
- Giải vở bài tập Sinh học 9
- Lý thuyết Sinh học 9
- Giải sbt Sinh học 9
- Giải sgk Vật Lí 9 (sách mới) | Giải bài tập Vật lí 9
- Giải sbt Vật Lí 9
- Lý thuyết Vật Lí 9
- Các dạng bài tập Vật lí lớp 9
- Giải vở bài tập Vật lí 9
- Giải sgk Địa Lí 9 (sách mới) | Giải bài tập Địa lí 9
- Lý thuyết Địa Lí 9
- Giải Tập bản đồ Địa Lí 9
- Giải sgk Tin học 9 (sách mới) | Giải bài tập Tin học 9
- Lý thuyết Tin học 9
- Lý thuyết Giáo dục công dân 9
- Giải vở bài tập Lịch sử 9
- Giải Tập bản đồ Lịch sử 9
- Lý thuyết Lịch sử 9
- Lý thuyết Công nghệ 9

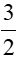 ; y ∈ R
; y ∈ R