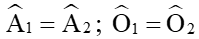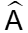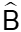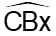Giáo án Tính chất của hai tiếp tuyến cắt nhau mới nhất - Toán 9
Với Giáo án Tính chất của hai tiếp tuyến cắt nhau mới nhất Toán lớp 9 được biên soạn bám sát sách Toán 9 giúp Thầy/ Cô biên soạn giáo án dễ dàng hơn.
Giáo án Toán 9 Bài 6: Tính chất của hai tiếp tuyến cắt nhau
I. Mục tiêu
Qua bài này giúp HS:
1. Kiến thức
- Phát biểu được các tính chất của hai tiếp tuyến cắt nhau, đường tròn nội tiếp tam giác, tam giác ngoại tiếp đường tròn, đường tròn bàng tiếp tam giác.
- Vẽ được đường tròn nội tiếp một tam giác cho trước.
- Vận dụng tính chất của hai tiếp tuyến cắt nhau vào bài tập tính toán hoặc chứng minh.
- Tìm tâm của một vật hình tròn bằng “thước phân giác”.
2. Kỹ năng
Vận dụng được các khái niệm để giải các bài tập có liên quan.
Thành thạo kĩ năng vẽ hình, kĩ năng tìm tâm của một hình tròn.
Rèn kĩ năng chứng minh.
3. Thái độ
- Nghiêm túc và hứng thú học tập.
- Chú ý lắng nghe, hăng hái phát biểu ý kiến xây dựng bài.
4. Định hướng năng lực, phẩm chất
- Năng lực tính toán,
- Năng lực giải quyết vấn đề,
- Năng lực hợp tác.
- Năng lực ngôn ngữ.
- Năng lực giao tiếp.
- Năng lực tự học.
Phẩm chất: Tự tin, tự chủ.
II. Chuẩn bị
- Gv : Giáo án, sách GK- SBt, phấn mầu, bảng nhóm.
- Hs: Đồ dùng học tập, đọc trước bài., sách GK – SBT – vở ghi.
III. Phương tiện và đồ dùng dạy học
- Thước, bút dạ, bảng phụ, bảng nhóm.
IV. Tiến trình dạy học
1. Ổn định:
2. Kiểm tra bài cũ: (Thông qua)
3. Bài mới:
Gv ĐVĐ: Ở các tiết học trước các em đã được biết thế nào là tiếp tuyến của đường tròn, tính chất của tiếp tuyến và các dấu hiệu nhận biết một đường thẳng là tiếp tuyến của đường tròn, vậy tiếp tuyến của đường tròn còn có các tính chất nào khác, chúng ta tiếp tục nghiên cứu ở bài học ngày hôm nay
| Giáo viên | Học sinh | Nội dung ghi bài |
|---|---|---|
|
Hoạt động hình thành kiến thức ND 1: Định lý về hai tiếp tuyến cắt nhau – 17p - Mục tiêu: HS nêu được định lí về hai tiếp tuyến cắt nhau. - Phương pháp: Nêu vấn đề - Kĩ thuật sử dụng: Kĩ thuật động não, trực quan, quan sát. - Năng lực: Tính toán, giải quyết vấn đề. |
||
|
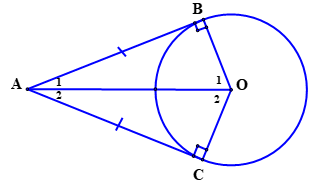
GV cho HS làm ?1 GV yêu cầu HS vẽ hình vào vở ? AB, AC là hai tiếp tuyến của (O) nó có tính chất gì ? ? Hãy chỉ ra cạnh và góc bằng nhau ? GV: ? Từ kết quả trên hãy cho biết 2 tiếp tuyến cắt nhau có tính chất gì ? GV giới thiệu định lý ? Từ hình vẽ trên và Nội dung định lý ghi GT-KL GV yêu cầu HS đọc Nội dung chứng minh sgk GV giới thiệu thước phân giác và yêu cầu HS làm ?2 ? Để tìm tâm hình tròn bằng thước phân giác vận dụng kiến thức nào ? |
HS đọc Nội dung ?1 HS vẽ hình – quan sát hình trả lời câu hỏi của ?1 HS :OB ⊥ AB; OC ⊥ AC HS: OB = OC = R; AB = AC HS trả lời HS đọc định lý 1 HS đứng tại chỗ nêu GT, KL HS tìm hiểu Nội dung chứng minh sgk HS tìm hiểu về thước phân giác và làm ?2 HS: tính chất hai tiếp tuyến cắt nhau |
1. Định lý về 2 tiếp tuyến cắt nhau: ?1 OB = OC = R; AB = AC * Định lý: (SGK – tr114) AB, AC : tiếp tuyến của (O) B, C: tiếp điểm => AB = AC AO: phân giác của OA: phân giác của CM: (SGK) ?2 Đặt miếng gỗ hình tròn tiếp xúc với hai cạnh của thước. Kẻ hai tia phân giác suy ra giao của hai tia phân giác là tâm của đường tròn. |
|
ND 2: Đường tròn nội tiếp tam giác - 15p - Mục tiêu: HS nêu được định nghĩa đường tròn nội tiếp tam giác, xác định được tâm đường tròn nội tiếp tam giác. - Phương pháp: Nêu vấn đề - Kĩ thuật sử dụng: Kĩ thuật động não, trực quan. - Năng lực: Tính toán, giải quyết vấn đề. |
||
|
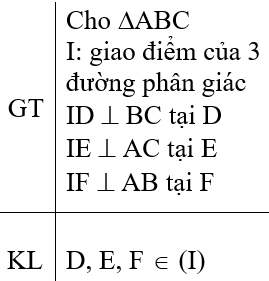
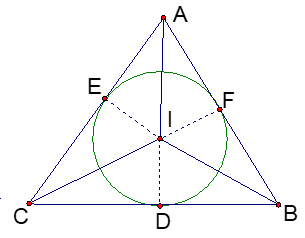
? Nhắc lại định nghĩa đường tròn ngoại tiếp tam giác ? Tâm đường tròn ngoại tiếp tam giác được xác định ntn? GV yêu cầu HS làm ?3 GV yêu cầu HS ghi GT, KL HS thảo luận nhóm những câu hỏi của GV NV1? Chứng minh D, E, F nằm trên cùng 1 đường tròn ta chứng minh ntn ? HD: GV: Những điểm thuộc tia phân giác của 1 góc thì sẽ có t/c gì? GV: I thuộc tia p/g của ta sẽ suy ra được điều gì? GV: tương tự ta sẽ suy ra được điều gì? GV: từ đó ta suy ra được IE = ID = IF hay 3 điểm D, E, F thuộc (I) GV: (I) tiếp xúc với 3 cạnh của ΔABC ta gọi (I) là đường tròn Nội tiếp ΔABC và ΔABC gọi là Δ ngoại tiếp đường tròn ? Vậy thế nào là đường tròn nội tiếp tam giác ? ? Xác định tâm của đường tròn nội tiếp tam giác ntn ? ? Cho 1 tam giác muốn vẽ đường tròn nội tiếp tam giác ta vẽ ntn ? |
HS trả lời câu hỏi của GV HS suy nghĩ làm ?3 HS ghi GT, KL HS ta phải chứng minh được: ID = IC = IF HS : Những điểm thuộc tia phân giác của 1 góc thì cách đều 2 cạnh của góc ấy HS: IE = IF HS: IF = ID và ID = IE HS nêu khái niệm SGK tr 114 HS: xác định giao của 3 đường phân giác trong của tam giác HS kẻ 2 đường phân giác của 2 góc trong tam giác |
2. Đường tròn nội tiếp tam giác: ?3 Chứng minh: + Vì I thuộc tia p/g của => IE = IF + Vì I thuộc tia p/g của => ID = IF => ID = IE = IF => 3 điểm D, E, F (I) * Khái niệm : Đường tròn tiếp xúc với 3 cạnh của tam giác là đường tròn nội tiếp tam giác. + Tâm của đường tròn nội tiếp tam giác là giao của 3 đường phân giác. + Khoảng cách từ tâm đến 3 cạnh là bán kính của đtròn nội tiếp tam giác |
|
ND 3: Đường tròn bàng tiếp – 10p Mục tiêu: HS nêu được định nghĩa đường tròn bàng tiếp tam giác, xác định được tâm đường tròn bàng tiếp tam giác. - Phương pháp: Nêu vấn đề, trực quan, quan sát. - Kĩ thuật sử dụng: Kĩ thuật động não, KWL. - Năng lực: Tính toán, giải quyết vấn đề. |
||
|
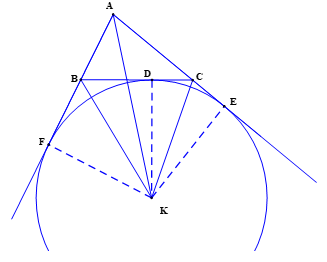
GV cho HS làm ?4 ? Hãy chứng minh 3 điểm D, E, F cùng nằm trên cùng 1 đường tròn tâm K ? GV: (K) tiếp xúc với cạnh BC và phần kéo dài của 2 cạnh AB và AC nên (K) gọi là đtròn bàng tiếp ΔABC ? Vậy thế nào là đường tròn bàng tiếp ? ? Tâm của đường tròn bàng tiếp nằm ở vị trí nào ? ? Một tam giác có mấy đường tròn bàng tiếp ? ? Có mấy vị trí của tam giác và đường tròn? ? Cho 1 tam giác bất kỳ có mấy đường tròn Nội tiếp, mấy đường tròn ngoại tiếp, mấy đường tròn bàng tiếp |
HS suyghĩ làm ?4 HS : + Vì K ∈ tia phân giác của => KD = KF + Vì K ∈ tia phân giác của => KD = KE => KE = KD = KF => 3 điểm D, E, F ∈ (K) HS trả lời HS: tâm của đường tròn bàng tiếp tam giác là giao 2 đường phân giác ngoài và 1 đường phân giác trong HS 3 đường tròn HS: tam giácngoại tiếp đường tròn ; tam giác Nội tiếp đường tròn đường tròn bàng tiếp HS trả lời |
3. Đường tròn bàng tiếp tam giác: ?4 + Vì K ∈ tia phân giác của => KD = KF + Vì K ∈ tia phân giác của => KD = KE => KE = KD = KF => 3 điểm D, E, F (K) * Khái niệm : + Đtròn bàng tiếp tam giác là đtròn tiếp xúc với 1 cạnh và phần kéo dài của 2 cạnh còn lại. + Tâm của đường tròn bàng tiếp tam giác là giao 2 đường phân giác ngoài và 1 đường phân giác trong |
|
C. Hoạt động tìm tòi, mở rộng:– 3p - Mục tiêu: - HS chủ động làm các bài tập về nhà để củng cố kiến thức đã học. - HS chuẩn bị bài mới giúp tiếp thu tri thức sẽ học trong buổi sau. - Phương pháp và kĩ thuật sử dụng: Kĩ thuật viết tích cực - Năng lực: Giải quyết vấn đề, ngôn ngữ. |
||
|
- Học thuộc định lý về tính chất của hai tiếp tuyến cắt nhau - Phân biệt định nghĩa; cách xác định tâm của đường tròn ngoại tiếp, Nội tiếp, bàng tiếp tam giác - BTVN: 26; 27; 28 (SGK); 48, 51 (SBT) - Chuẩn bị tiết luyện tập - Tìm ví dụ thực tế về tính chất 2 tiếp tuyến cắt nhau. |
||
Xem thêm các bài Giáo án Toán lớp 9 hay, chi tiết khác:
Giáo án Vị trí tương đối của hai đường tròn
Xem thêm các chương trình khác:
- Giải sgk Hóa học 9 (sách mới) | Giải bài tập Hóa 9
- Giải sbt Hóa học 9
- Giải vở bài tập Hóa học 9
- Lý thuyết Hóa học 9
- Các dạng bài tập Hóa học lớp 9
- Tóm tắt tác phẩm Ngữ văn 9 (sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Soạn văn 9 (hay nhất) | Để học tốt Ngữ văn 9 (sách mới)
- Soạn văn 9 (ngắn nhất)
- Văn mẫu 9 (sách mới) | Để học tốt Ngữ văn 9 Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Tác giả - tác phẩm Ngữ văn 9 (sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Giải sgk Tiếng Anh 9 (thí điểm)
- Giải sgk Tiếng Anh 9 (sách mới) | Để học tốt Tiếng Anh 9
- Giải sbt Tiếng Anh 9
- Giải sbt Tiếng Anh 9 (thí điểm)
- Giải sgk Sinh học 9 (sách mới) | Giải bài tập Sinh học 9
- Giải vở bài tập Sinh học 9
- Lý thuyết Sinh học 9
- Giải sbt Sinh học 9
- Giải sgk Vật Lí 9 (sách mới) | Giải bài tập Vật lí 9
- Giải sbt Vật Lí 9
- Lý thuyết Vật Lí 9
- Các dạng bài tập Vật lí lớp 9
- Giải vở bài tập Vật lí 9
- Giải sgk Địa Lí 9 (sách mới) | Giải bài tập Địa lí 9
- Lý thuyết Địa Lí 9
- Giải Tập bản đồ Địa Lí 9
- Giải sgk Tin học 9 (sách mới) | Giải bài tập Tin học 9
- Lý thuyết Tin học 9
- Lý thuyết Giáo dục công dân 9
- Giải vở bài tập Lịch sử 9
- Giải Tập bản đồ Lịch sử 9
- Lý thuyết Lịch sử 9
- Lý thuyết Công nghệ 9

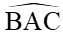 gọi là góc tạo bởi 2 tiếp tuyến AB và AC;
gọi là góc tạo bởi 2 tiếp tuyến AB và AC;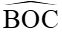 gọi là góc tạo bởi 2 bán kính OB và OC (là 2 bán kính đi qua 2 tiép điểm)
gọi là góc tạo bởi 2 bán kính OB và OC (là 2 bán kính đi qua 2 tiép điểm)