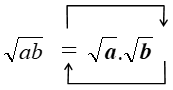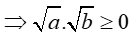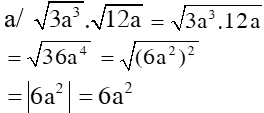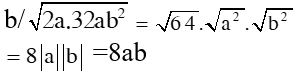Giáo án Liên hệ giữa phép nhân và phép khai phương mới nhất - Toán 9
Với Giáo án Liên hệ giữa phép nhân và phép khai phương mới nhất Toán lớp 9 được biên soạn bám sát sách Toán 9 giúp Thầy/ Cô biên soạn giáo án dễ dàng hơn.
Giáo án Toán 9 Bài 3: Liên hệ giữa phép nhân và phép khai phương
I. Mục tiêu
Qua bài này giúp HS:
1. Kiến thức
- Phát biểu được nội dung và cách chứng minh định lý về liên hệ giữa phép nhân và phép khai phương.
- Phát hiện được liên hệ giữa phép khai phương với quan hệ thứ tự và dùng liên hệ này để so sánh các số.
2. Kỹ năng
- Dùng được các quy tắc khai phương một tích và nhân các căn bậc hai trong tính toán và biến đổi biểu thức.
3. Thái độ
- Nghiêm túc và hứng thú học tập, tư duy logic.
4. Định hướng năng lực, phẩm chất
- Giúp học sinh phát huy năng lực tính toán, năng lực giải quyết vấn đề, năng lực hợp tác, năng lực ngôn ngữ, năng lực tự học.
Phẩm chất: Tự tin, tự chủ
II. Chuẩn bị
- Gv : Phấn mầu, bảng phụ, thước thẳng.
- Hs: Đồ dùng học tập, đọc trước bài.
III. Tiến trình dạy học
1. Ổn định: (1 phút)
2. Bài học
| Giáo viên | Học sinh | Nội dung ghi bài |
|---|---|---|
| A - Hoạt động khởi động (1p) | ||
|
Ở các bài học trước các em đã nắm được điều kiện để căn thức có nghĩa và biết áp dụng hằng đẳng thức |
||
|
B – Hoạt động hình thành kiến thức – 30p *Mục tiêu: Hs nắm được định lý, nắm được quy tắc nhân các căn bậc hai và quy tắc khai phương một tích . *Giao nhiệm vụ: +Chứng minh được định lý, nắm được quy tắc khai phương một tích và nhân các căn bậc hai +Làm được các ví dụ trong SGK và bài ?1,?2,?3,?4 *Cách thức hoạt động: +Các ví dụ: Hoạt động cá nhân,cặp đôi +?1,?2,?3,?4: Hoạt động nhóm |
||
|
*Thực hiện nhiệm vụ: GV cho HS làm bài ?1 theo cá nhân. Tính và so sánh: √16.25 và √16.√25 Gọi một HS đứng tại chỗ trả lời ? Tổng quát với 2 số không âm a, b ta có điều gì? GV giới thiệu định lý ?Theo định nghĩa căn bậc hai số học, để chứng minh √a, √b là căn bậc hai số học của a.b thì phải chứng minh những gì? Định lý trên còn có thể mở rộng cho tích của nhiều số không âm. Từ định lý này , người ta phát biểu được hai quy tắc theo hai chiều ngược nhau Với |
HS làm ?1 theo cá nhân HS đứng tại chỗ trả lời Hs: √16.25 = √400 = 20 √16. √25 = 4.5 = 20 => √16.25 = √16. √5 HS dựa vào ví dụ khái quát về liên hệ giữa phép nhân và phép khai phương Ta phải chứng minh √a.√b xác định, không âm và (√a. √b )2=a.b HS nêu cm miệng |
1. Định lý ?1/Tr12 √16.25 = √400 = 20 √16. √25= 4.5 = 20 Vậy √16.25 = √16. √25 Định lý: SGK/12 CM: Ta có: Vì a Nên √a, √b xác định và không âm => Khi đó : (√a. √b)2 = (√a)2. (√b)2 = ab Vậy √a.√b = √ab |
|
GV giới thiệu quy tắc khai phương một tích và cho HS nhắc lại nội dung của quy tắc. Hướng dẫn HS làm ví dụ 1 Yêu cầu HS làm ?2 để củng cố. Gọi hai HS lên bảng thực hiện. Gọi HS nhận xét bài làm GV nhận xét và sửa sai GV giới thiệu quy tắc nhân các căn thức bậc hai và cho HS nhắc lại nội dung của quy tắc. Hướng dẫn HS làm ví dụ 2 Yêu cầu HS làm ?3 để củng cố. Gọi hai HS lên bảng thực hiện. Gọi HS nhận xét bài làm GV nhận xét và sửa sai GV giới thiệu chú ý. Áp dụng chú ý đó ta có thể rút gọn biểu thức chứa căn thức bậc hai. GV giới thiệu ví dụ 3/14 Cho HS làm ?4 để củng cố lại chú ý và ví dụ 3. Gọi hai HS lên bảng làm bài. Gọi HS dưới lớp nhận xét bài làm của bạn. GV nhận xét và sửa sai. |
HS nhắc lại nội dung của quy tắc. HS nghe GV hướng dẫn HS cả lớp làm ?2 vào vở của mình theo cá nhân để củng cố quy tắc. Hai HS lên bảng thực hiện. HS cả lớp nhận xét và bổ sung HS nhắc lại nội dung của quy tắc. HS nghe GV hướng dẫn HS cả lớp làm ?2 vào vở của mình theo cá nhân để củng cố quy tắc. Hai HS lên bảng thực hiện. HS cả lớp nhận xét và bổ sung HS quan sát GV thực hiện HS làm ?4 theo cá nhân vào vở. Hai HS lên bảng làm bài HS cả lớp nhận xét bài làm của bạn |
2. Áp dụng a/ Quy tắc khai phương một tích: SGK/13 * Ví dụ 1: Xem SGK/13 ?2/ Tr13 a/ √0,16.0,64.225 = √0,16. √0,64 .√225 =0,4.0,8.15 =4,8 b/ √225.360 = √25.36.100 = √25. √36. √100 =5.6.10 =300 b/ Quy tắc nhân các căn thức bậc hai: SGK/13 *Ví dụ 2: Xem SGK/13 ?3/14 a/ √3. √75 = √3.75 = √225 = 15 b/ √20. √72. √4,9 = √20.72.4,9 = √4. √36. √49 = 2.6.7 = 84 Chú ý: Xem SGK/14 ?4/14 |
|
C - Hoạt động luyện tập – 10p *Mục tiêu: Hs biết vận dụng quy tắc khai phương một thương và nhân các căn thức bậc hai vào làm các bài toán rút gọn biểu thức và dạng tính toán dạng phức tạp hơn *Giao nhiệm vụ: Làm bài tập 20(SGK),bài 27(SBT) *Cách thức hoạt động: +Giao nhiệm vụ: Hoạt động nhóm |
||
|
+Thực hiện nhiệm vụ: Bài 20: Bài 27 (SBT) +Gv yêu cầu các nhóm nhận xét lẫn nhau rồi chốt lại vấn đề |
||
| D – Tìm tòi, mở rộng – 3p | ||
|
Mục tiêu: - HS chủ động làm các bài tập về nhà để củng cố kiến thức đã học. - HS chuẩn bị bài mới giúp tiếp thu tri thức sẽ học trong buổi sau. - Yêu cầu HS nhắc lại hai quy tắc đã học. Cần chú ý ta có thể áp dụng hai quy tắc đó sao cho tính toán nhanh và chính xác - Bài tập về nhà: 17, 18, 19, 20, 21, 22 /14,15 SGK. Hướng dẫn: Bài 17 c/ Chú ý √12,1.360 = √121.36 vì √121 và √36 nhẩm được kết quả thứ tự là 11 và 6 Bài 18 làm tương tự như ?3 Bài 19, 20 chú ý đến điều kiện xác định của các căn thức. |
||
Xem thêm các bài Giáo án Toán lớp 9 hay, chi tiết khác:
Giáo án Liên hệ giữa phép chia và phép khai phương
Giáo án Biến đổi đơn giản biểu thức chứa căn thức bậc hai
Giáo án Biến đổi đơn giản biểu thức chứa căn thức bậc hai (tiếp theo)
Xem thêm các chương trình khác:
- Giải sgk Hóa học 9 (sách mới) | Giải bài tập Hóa 9
- Giải sbt Hóa học 9
- Giải vở bài tập Hóa học 9
- Lý thuyết Hóa học 9
- Các dạng bài tập Hóa học lớp 9
- Tóm tắt tác phẩm Ngữ văn 9 (sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Soạn văn 9 (hay nhất) | Để học tốt Ngữ văn 9 (sách mới)
- Soạn văn 9 (ngắn nhất)
- Văn mẫu 9 (sách mới) | Để học tốt Ngữ văn 9 Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Tác giả - tác phẩm Ngữ văn 9 (sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Giải sgk Tiếng Anh 9 (thí điểm)
- Giải sgk Tiếng Anh 9 (sách mới) | Để học tốt Tiếng Anh 9
- Giải sbt Tiếng Anh 9
- Giải sbt Tiếng Anh 9 (thí điểm)
- Giải sgk Sinh học 9 (sách mới) | Giải bài tập Sinh học 9
- Giải vở bài tập Sinh học 9
- Lý thuyết Sinh học 9
- Giải sbt Sinh học 9
- Giải sgk Vật Lí 9 (sách mới) | Giải bài tập Vật lí 9
- Giải sbt Vật Lí 9
- Lý thuyết Vật Lí 9
- Các dạng bài tập Vật lí lớp 9
- Giải vở bài tập Vật lí 9
- Giải sgk Địa Lí 9 (sách mới) | Giải bài tập Địa lí 9
- Lý thuyết Địa Lí 9
- Giải Tập bản đồ Địa Lí 9
- Giải sgk Tin học 9 (sách mới) | Giải bài tập Tin học 9
- Lý thuyết Tin học 9
- Lý thuyết Giáo dục công dân 9
- Giải vở bài tập Lịch sử 9
- Giải Tập bản đồ Lịch sử 9
- Lý thuyết Lịch sử 9
- Lý thuyết Công nghệ 9

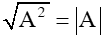 để làm các bài toán tính toán và rút gọn biểu thức.Tuy nhiên để làm được các dạng bài tập về căn thức ta cần nắm được các quy tắc về phép tính trên căn thức. Bài học hôm nay giúp ta nắm được liên hệ giữa phép nhân và phép khai phương.
để làm các bài toán tính toán và rút gọn biểu thức.Tuy nhiên để làm được các dạng bài tập về căn thức ta cần nắm được các quy tắc về phép tính trên căn thức. Bài học hôm nay giúp ta nắm được liên hệ giữa phép nhân và phép khai phương.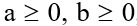 , ta có:
, ta có: