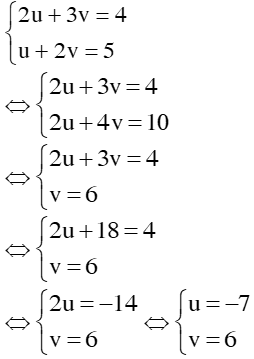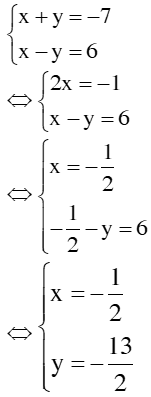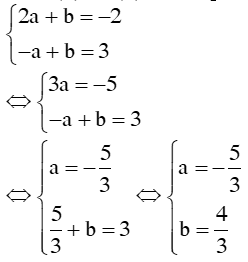Giáo án Luyện tập trang 19-20 (Tập 2) mới nhất - Toán 9
Với Giáo án Luyện tập trang 19-20 (Tập 2) mới nhất Toán lớp 9 được biên soạn bám sát sách Toán 9 giúp Thầy/ Cô biên soạn giáo án dễ dàng hơn.
Giáo án Toán 9 Luyện tập trang 19-20 (Tập 2)
I. Mục tiêu
Qua bài này giúp HS:
1. Kiến thức
- Nhắc lại được cách giải hệ phương trình bằng phương pháp cộng đại số, phương pháp thế.
- Vận dụng được kiến thức để giải hệ phương trình bằng phương pháp cộng đại số, qua đó mở rộng với các bài chứa tham số. (làm được bài tập)
- HS có mối liên hệ tương ứng giữa nghiệm của hệ hai phương trình và số giao điểm của 2 đường thẳng, bước đầu áp dụng tìm nghiệm của hệ và bài toán tìm tọa độ giao điểm của hai đường thẳng cho trước. (B26-SGK)
2. Kỹ năng
- Nhận biết được hệ phương trình để có cách giải phù hợp nhất.
- Ren kĩ năng trình bày giải hệ phương trình thành thạo, chính xác.
3. Thái độ
- Nghiêm túc và hứng thú học tập.
- Yêu thích môn học.
4. Định hướng năng lực, phẩm chất
- Năng lực tính toán
- Năng lực giải quyết vấn đề
- Năng lực hợp tác.
- Năng lực ngôn ngữ
- Năng lực giao tiếp.
- Năng lực tự học.
Phẩm chất: Tự tin, tự chủ.
II. Chuẩn bị
- Gv : Thước thẳng, bảng phụ, phấn mầu, máy tính casio.
- Hs : Học bài, chuẩn bị bài ở nhà, máy tính casio.
III. Tiến trình dạy học
1. Ổn định
2. Nội dung
| Giáo viên | Học sinh | Nội dung ghi bài |
|---|---|---|
|
Hoạt động 1: Khởi động – 10p Mục tiêu: HS biết giải HPT bằng 2 phương pháp PP: Vấn đáp, thuyết trình |
||
|
GV nêu yêu cầu kiểm tra: Cho hpt HS1: Giải hpt trên = pp thế HS2: Giải hpt trên = pp cộng đại số GV nx, cho điểm |
2 HS lên bảng kiểm tra HS1: Giải hpt = pp thế Vậy hpt có 1 nghiệm duy nhất: (x; y) = (3; 4) HS2: giải hpt = pp cộng đại số Vậy hpt có 1 nghiệm duy nhất: (x; y) = (3; 4) HS lớp nx, chữa bài |
|
|
Họat động 2: Luyện tập – 33p Mục tiêu: HS biết giải HPT bằng pp cộng |
||
|
GV yêu cầu HS làm bài tập 22(SGK – tr19) - GV: vì hệ số của ẩn y trong 2pt nhỏ hơn hệ số của ẩn x -> nên khử ẩn y ? Ta khử ẩn y ntn? GV gọi 1 HS lên bảng GV nhận xét bài làm của HS GV yêu cầu 1HS lên bảng làm câu b GV lưu ý: phương trình 0x + 0y = c (với c là 1 số khác 0) vô nghiệm => hpt đã cho vô nghiệm GV gọi 1 HS lên bảng làm câu c ? trước hết ta phải làm gì? Ta sẽ được hpt nào? ? Ta giải hệ này ntn? GV: pt 0x + 0y = 0 là 1 pt luôn đúng với mọi x,y. Vậy hpt đã cho có bao nhiêu nghiệm? Và CT nghiệm TQ là gì? GV yêu cầu HS làm bài tập 24ª SGK GV: Hpt đã có dang TQ của hpt bậc nhất 2 ẩn chưa? ? Làm cách nào để đưa về dạng TQ? GV yêu cầu 1 HS lên bảng làm GV nhận xét bài làm của HS và hướng dẫn HS giải hpt này theo cách 2 bằng pp đặt ẩn phụ: Đặt x + y = u; x – y = v. Khi đó hpt đã cho trở thành hpt nào? Với ẩn là ẩn nào? GV hãy giải hpt này GV: Sau khi giải xong hpt với biến mới, các em phải thay trở lại bước đổi biến để tìm biến ban đầu Cụ thể: Thay GV: pp đặt ẩn phụ được dùng nhiều trong TH hpt có biểu thức lặp lại nhiều lần. Tuy nhiên khi đặt ẩn phụ các em cần lưu y tới đk nếu có GV yêu cầu HS làm bài tập 26a(SGK) ?Với GT đồ thị hsố đi qua 2 điểm A và B đã biết tọa độ ta sẽ có được điều gì? ? Với A(2; – 2) thuộc đồ thị hsố ta sẽ có được hệ thức nào? Hãy đưa về pt bậc nhất 2 ẩn a, b ? Tương tự với điểm B Từ (1) và (2) ta có hpt nào ? Giải hpt này tìm a, b |
HS làm bài tập 22 HS: Nhân 2 vế của pt(1) với 3 và nhân 2 vế của pt(2) với 2 HS: Vậy hpt có 1 nghiệm duy nhất: (x; y) = HS lớp nhận xét, chữa bài Vậy hpt đã cho vô nghiệm HS: Nhân cả 2 vế của pt(2) với 3, ta được hpt: HS: trừ từng vế của 2 pt: HS: hpt có vô số nghiệm, nghiệm TQ của hpt là: HS suy nghĩ làm bài tập 24 HS: Hpt chưa có dạng TQ HS: Áp dụng qtắc bỏ ngoặc HS: Vậy hpt có 1 nghiệm duy nhất: HS: hpt trở thành: HS suy nghĩ làm bài tập 26 HS: Tọa độ 2 điểm A, B sẽ thỏa mãn CT hsố y = ax + b HS: – 2 = a.2 + b <=> 2a + b = – 2 (1) HS: Vì B(– 1; 3) thuộc đồ thị hsố nên ta có: 3 = a.(– 1) + b <=> – a + b = 3 (2) HS: Từ (1) và (2) ta có hpt: Vậy HS lớp chữa bài |
1. Bài 22(SGK – tr19): a. Vậy hpt có 1 nghiệm duy nhất: (x; y) = b. Vậy hpt đã cho vô nghiệm c. <=> Vậy hpt có vô số nghiệm, nghiệm TQ của hpt là: 2. Bài 24(SGK – tr19): a. * Cách 1: Vậy hpt có 1 nghiệm duy nhất: * Cách 2: Đặt Thay ta được: Vậy hpt có 1 nghiệm duy nhất: 3. Bài 26(SGK – tr19): Xác định hệ số a, b của đồ thị hsố y = ax + b đi qua 2 điểm A, B trong trường hợp sau: a. A(2; – 2) và B(– 1; 3) Giải: + Vì A(2; – 2) thuộc đồ thị hsố nên ta có: – 2 = a.2 + b <=> 2a + b = – 2 (1) + Vì B(– 1; 3) thuộc đồ thị hsố nên ta có: 3 = a.(– 1) + b <=> – a + b = 3(2) + Từ (1) và (2) ta có hpt: Vậy |
|
Hoạt động 3: Tìm tòi, mở rộng. – 2p - Mục tiêu: - HS chủ động làm các bài tập về nhà để củng cố kiến thức đã học. - HS chuẩn bị bài mới giúp tiếp thu tri thức sẽ học trong buổi sau. - Kĩ thuật sử dụng: Kĩ thuật viết tích cực |
||
|
- Nắm vững các cách giải hpt. - BTVN: 23; 24b; 26 (SGK) - Chuẩn bị tiết luyện tập. |
||
Xem thêm các bài Giáo án Toán lớp 9 hay, chi tiết khác:
Giáo án Giải bài toán bằng cách lập hệ phương trình
Giáo án Giải bài toán bằng cách lập hệ phương trình (Tiếp theo)
Xem thêm các chương trình khác:
- Giải sgk Hóa học 9 (sách mới) | Giải bài tập Hóa 9
- Giải sbt Hóa học 9
- Giải vở bài tập Hóa học 9
- Lý thuyết Hóa học 9
- Các dạng bài tập Hóa học lớp 9
- Tóm tắt tác phẩm Ngữ văn 9 (sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Soạn văn 9 (hay nhất) | Để học tốt Ngữ văn 9 (sách mới)
- Soạn văn 9 (ngắn nhất)
- Văn mẫu 9 (sách mới) | Để học tốt Ngữ văn 9 Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Tác giả - tác phẩm Ngữ văn 9 (sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Giải sgk Tiếng Anh 9 (thí điểm)
- Giải sgk Tiếng Anh 9 (sách mới) | Để học tốt Tiếng Anh 9
- Giải sbt Tiếng Anh 9
- Giải sbt Tiếng Anh 9 (thí điểm)
- Giải sgk Sinh học 9 (sách mới) | Giải bài tập Sinh học 9
- Giải vở bài tập Sinh học 9
- Lý thuyết Sinh học 9
- Giải sbt Sinh học 9
- Giải sgk Vật Lí 9 (sách mới) | Giải bài tập Vật lí 9
- Giải sbt Vật Lí 9
- Lý thuyết Vật Lí 9
- Các dạng bài tập Vật lí lớp 9
- Giải vở bài tập Vật lí 9
- Giải sgk Địa Lí 9 (sách mới) | Giải bài tập Địa lí 9
- Lý thuyết Địa Lí 9
- Giải Tập bản đồ Địa Lí 9
- Giải sgk Tin học 9 (sách mới) | Giải bài tập Tin học 9
- Lý thuyết Tin học 9
- Lý thuyết Giáo dục công dân 9
- Giải vở bài tập Lịch sử 9
- Giải Tập bản đồ Lịch sử 9
- Lý thuyết Lịch sử 9
- Lý thuyết Công nghệ 9

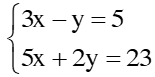
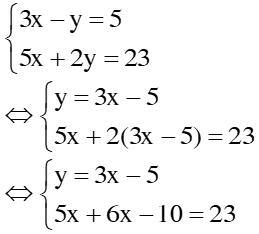
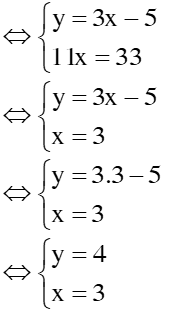
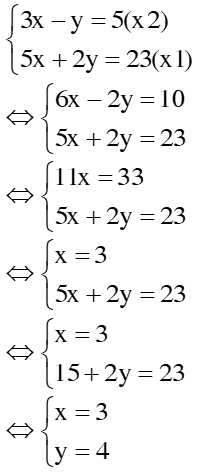
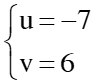 vào
vào 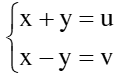 ta được:
ta được: 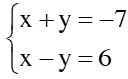 và giải tỉếp hpt này?
và giải tỉếp hpt này?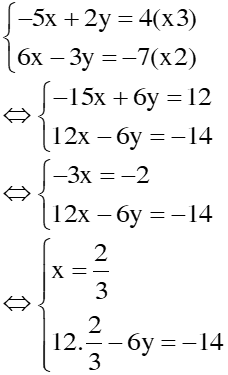
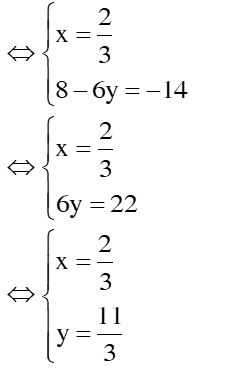
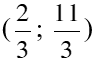
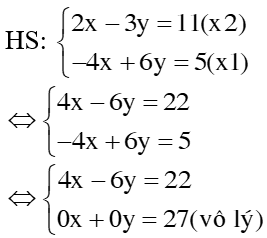
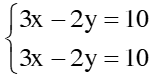

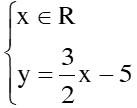
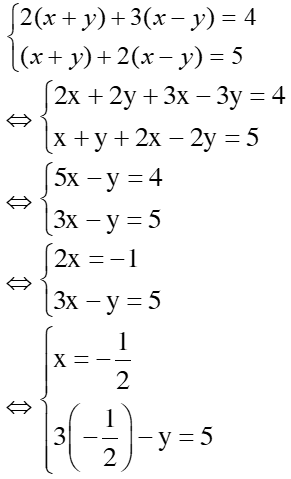
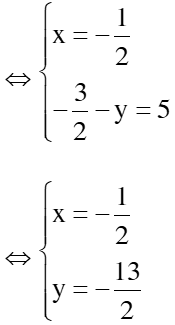
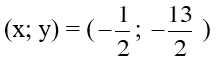
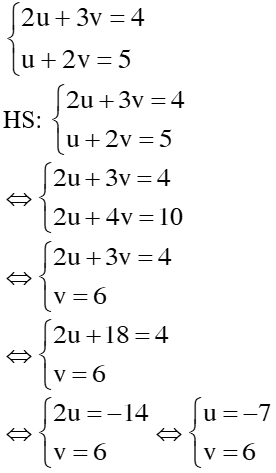
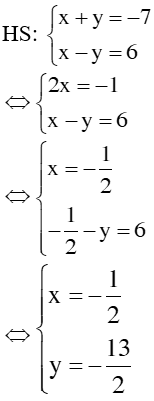
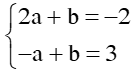
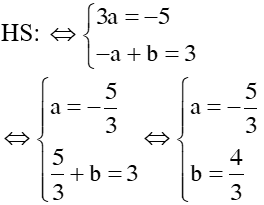
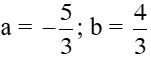
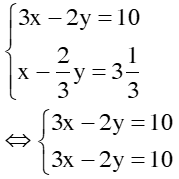
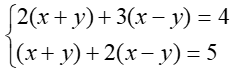
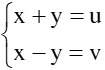 hpt đã cho trở thành:
hpt đã cho trở thành: