Nội dung bài viết

    Xem thêm

    Giải Toán 7 trang 82 Tập 2 Chân trời sáng tạo

    Với giải bài tập Toán lớp 7 trang 82 Tập 2 trong Bài 9: Tính chất ba đường phân giác của tam giác sách Chân trời sáng tạo hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 7 trang 82 Tập 2.

    1 793 18/01/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Giải Toán 7 trang 82 Tập 2

    Bài 2 trang 82 Toán 7 Tập 2:

    Cho tam giác ABC cân tại A. Kẻ đường trung tuyến AM. Tia phân giác của góc B cắt AM tại I. Chứng minh rằng CI là tia phân giác của góc C.

    Lời giải:

    GT

    ∆ABC cân tại A,

    Trung tuyến AM,

    Tia phân giác của góc B cắt AM tại I.

    KL

    CI là tia phân giác của góc C.

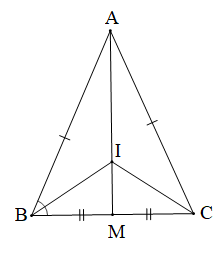
    Giải Toán 7 Bài 9 (Chân trời sáng tạo): Tính chất ba đường phân giác của tam giác (ảnh 1) 

    +) Tam giác ABC cân tại A (giả thiết) nên AB = AC.

    Lại có AM là đường trung tuyến (giả thiết) do đó MB = MC (M là trung điểm của BC)

    Xét ∆ABM và ∆ACM có:

    AB = AC (chứng minh trên),

    AM là cạnh chung,

    MB = MC (chứng minh trên)

    Do đó ∆ABM = ∆ACM (c.c.c)

    Suy ra BAM^=CAM^ (hai góc tương ứng)

    Suy ra AM là tia phân giác của BAC^ 

    +) Tam giác ABC có AM, BI là hai đường phân giác cắt nhau tại I

    Mà ba đường phân giác của tam cắt nhau tại một điểm nên I là giao điểm ba đường phân giác này.

    Do đó CI là tia phân giác của góc C.

    Vậy CI là tia phân giác của góc C.

    Bài 3 trang 82 Toán 7 Tập 2:

    Cho tam giác ABC cân tại A. Tia phân giác của các góc B và C cắt nhau tại M. Tia AM cắt BC tại H. Chứng minh rằng H là trung điểm của BC.

    Lời giải:

    GT

    ∆ABC cân tại A,

    BM, CM lần lượt là tia phân giác của góc B và C,

    Tia AM cắt BC tại H.

    KL

    H là trung điểm của BC.

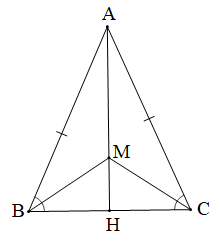
    Giải Toán 7 Bài 9 (Chân trời sáng tạo): Tính chất ba đường phân giác của tam giác (ảnh 1) 

    Tam giác ABC có tia phân giác của các góc B và C cắt nhau tại M (giả thiết)

    Mà ba đường phân giác của tam giác đồng quy tại một điểm nên AM là đường phân giác của góc A của tam giác ABC.

    Suy ra BAM^=CAM^ hay BAH^=CAH^.

    Tam giác ABC cân tại A (giả thiết) nên AB = AC và ABH^=ACH^.  

    Xét tam giác ABH và tam giác ACH có:

    BAH^=CAH^ (chứng minh trên);

    AB = AC (chứng minh trên);

    ABH^=ACH^(chứng minh trên).

    Do đó ∆ABH = ∆ACH (g.c.g)

    Suy ra BH = CH (hai cạnh tương ứng)

    Vậy H là trung điểm của BC.

    Bài 4 trang 82 Toán 7 Tập 2:

    Cho tam giác DEF. Tia phân giác của góc D và E cắt nhau tại I. Qua I kẻ đường thẳng song song với EF, đường thẳng này cắt DE tại M, cắt DF tại N. Chứng minh rằng ME + NF = MN.

    Lời giải:

    GT

    ∆DEF,

    DI, EI lần lượt là tia phân giác của góc D và I,

    M ∈ DE, N ∈ DF, MN // EF

    KL

    ME + NF = MN.

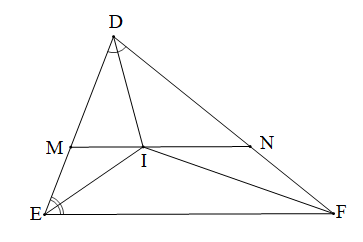
    Giải Toán 7 Bài 9 (Chân trời sáng tạo): Tính chất ba đường phân giác của tam giác (ảnh 1) 

    +) Vì EI là đường phân giác của E^ nên MEI^=IEF^.

    Lại có MN // EF (giả thiết) nên MIE^=IEF^ (hai góc so le trong).

    Suy ra MEI^=MIE^.

    Do đó tam giác MIE cân tại M nên ME = MI (1).

    +) Tam giác DEF có tia phân giác của góc D và E cắt nhau tại I (giả thiết)

    Mà ba đường phân giác của tam giác đồng quy tại một điểm nên I là giao điểm ba đường phân giác

    Do đó IF là đường phân giác của góc F, hay NFI^=IFE^.

    Lại có MN // EF nên NIF^=IFE^ (hai góc so le trong).

    Suy ra NFI^=NIF^.

    Do đó tam giác NIF cân tại N nên NI = NF (2).

    Từ (1) và (2) ta có ME + NF = MI + NI = MN.

    Vậy ME + NF = MN.

    Bài 5 trang 82 Toán 7 Tập 2:

    Cho tam giác AMN vuông tại A. Tia phân giác của góc M và N cắt nhau tại I. Tia MI cắt AN tại R. Kẻ RT vuông góc với AI tại T. Chứng minh rằng AT = RT.

    Lời giải:

    GT

    ∆AMN vuông tại A,

    Tia phân giác của góc M và N cắt nhau tại I,

    MI cắt AN tại R,

    RT ⊥ AI tại T

    KL

    AT = RT.

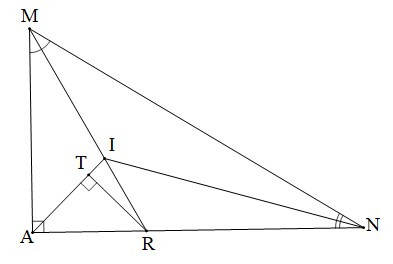
    Giải Toán 7 Bài 9 (Chân trời sáng tạo): Tính chất ba đường phân giác của tam giác (ảnh 1) 

    Tam giác AMN có hai đường phân giác của góc M và N cắt nhau tại I (giả thiết)

    Mà ba đường phân giác của tam giác đồng quy tại một điểm nên AI là đường phân giác của góc A.

    Do đó IAR^=12MAN^=12.90°=45°.

    Xét tam giác TAR vuông tại T có:

    TAR^+TRA^=90° (trong tam giác vuông, hai góc nhọn phụ nhau)

    Suy ra TRA^=90°−TAR^=90°−45°=45°.

    Tam giác TAR có TAR^=TRA^=45° nên tam giác TAR cân tại T.

    Do đó AT = RT.

    Bài 6 trang 82 Toán 7 Tập 2:

    Ba thành phố A, B, C được nối với nhau bởi ba xa lộ (Hình 9). Người ta muốn tìm một địa điểm để làm một sân bay sao cho địa điểm này phải cách đều ba xa lộ đó.

    Hãy xác định vị trí của sân bay thỏa mãn điều kiện trên và giải thích cách thực hiện.

    Giải Toán 7 Bài 9 (Chân trời sáng tạo): Tính chất ba đường phân giác của tam giác (ảnh 1) 

    Lời giải:

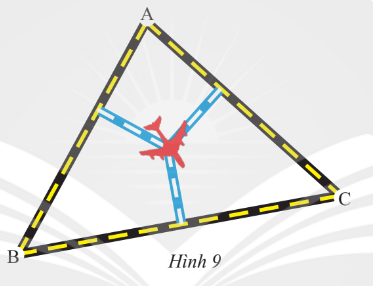
    Ba xa lộ tạo thành ba cạnh của tam giác ABC như Hình 9.

    Vì ba đường phân giác của tam giác cùng đi qua một điểm, điểm này cách đều ba cạnh của tam giác.

    Do đó để sân bay cách đều ba xa lộ AB, BC, CA thì địa điểm làm sân bay là giao điểm ba đường phân giác của tam giác ABC.

    Xem thêm lời giải bài tập Toán lớp 7 Chân trời sáng tạo hay, chi tiết khác: 

    Giải Toán 7 trang 79 Tập 2

    Giải Toán 7 trang 80 Tập 2

    Giải Toán 7 trang 81 Tập 2

    Giải Toán 7 trang 82 Tập 2

    Xem thêm lời giải bài tập Toán lớp 7 Chân trời sáng tạo hay, chi tiết khác:

    Khởi động trang 79 Toán 7 Tập 2: Điểm nào nằm bên trong tam giác và cách đều ba cạnh của tam giác...

    Khám phá 1 trang 79 Toán 7 Tập 2: Vẽ và cắt hình tam giác ABC rồi gấp hình sao cho cạnh AB trùng với cạnh AC ta được nếp gấp AD...

    Thực hành trang 79 Toán 7 Tập 2: Trong Hình 3, hãy vẽ các đường phân giác GM, EN và FP của tam giác EFG...

    Khám phá 2 trang 80 Toán 7 Tập 2: Vẽ một tam giác trên giấy. Cắt rời tam giác ra khỏi tờ giấy rồi gấp hình tam giác đó để xác định ba đường phân giác...

    Vận dụng trang 81 Toán 7 Tập 2: Một nông trại nằm trên mảnh đất hình tam giác có ba cạnh tường rào tiếp giáp với ba con đường (Hình 7)...

    Bài 1 trang 81 Toán 7 Tập 2: Trong Hình 8, I là giao điểm ba đường phân giác của tam giác ABC.a) Cho biết IM = 6 (Hình 8a). Tính IK và IN...

    Bài 2 trang 82 Toán 7 Tập 2: Cho tam giác ABC cân tại A. Kẻ đường trung tuyến AM. Tia phân giác của góc B cắt AM tại I...

    Bài 3 trang 82 Toán 7 Tập 2: Cho tam giác ABC cân tại A. Tia phân giác của các góc B và C cắt nhau tại M. Tia AM cắt BC tại H...

    Bài 4 trang 82 Toán 7 Tập 2: Cho tam giác DEF. Tia phân giác của góc D và E cắt nhau tại I. Qua I kẻ đường thẳng song song với EF...

    Bài 5 trang 82 Toán 7 Tập 2: Cho tam giác AMN vuông tại A. Tia phân giác của góc M và N cắt nhau tại I. Tia MI cắt AN tại R...

    Bài 6 trang 82 Toán 7 Tập 2: Ba thành phố A, B, C được nối với nhau bởi ba xa lộ (Hình 9). Người ta muốn tìm một địa điểm để làm một sân bay...

    Xem thêm lời giải bài tập Toán lớp 7 Chân trời sáng tạo hay, chi tiết khác:  

    Bài 8: Tính chất ba đường cao của tam giác

    Bài 9: Tính chất ba đường phân giác của tam giác

    Bài 10: Hoạt động thực hành và trải nghiệm. Làm giàn hoa tam giác để trang trí lớp học

    Bài tập cuối chương 8

    Câu hỏi trang 85 Toán 7 Tập 2

    Tham khảo các loạt bài Toán 7 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 793 18/01/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: