Giải Toán 7 Bài 2 (Cánh diều): Đa thức một biến. Nghiệm của đa thức một biến

Giải bài tập Toán 7 Bài 2: Đa thức một biến. Nghiệm của đa thức một biến

A. Câu hỏi

Giải Toán 7 trang 47 Tập 2

Câu hỏi khởi động trang 47 Toán 7 Tập 2:

Trong giờ học môn Mĩ thuật, bạn Hạnh dán lên trang vở hai hình vuông có kích thước lần lượt là 3 cm và x cm như ở Hình 1. Tổng diện tích của hai hình vuông đó là x² + 9 (cm²).

Biểu thức đại số x² + 9 có gì đặc biệt?

Lời giải:

Sau bài học này chúng ta sẽ giải quyết được câu hỏi trên như sau:

Biểu thức đại số x² + 9 biểu thị tổng diện tích của hai hình vuông là đa thức một biến x.

Hoạt động 1 trang 47 Toán 7 Tập 2:

a) Viết biểu thức biểu thị:

- Diện tích của hình vuông có độ dài cạnh là x cm;

- Thể tích của hình lập phương có độ dài cạnh là 2x cm.

b) Các biểu thức trên có dạng như thế nào?

Lời giải:

a) - Biểu thức biểu thị diện tích của hình vuông có độ dài cạnh là x cm là: x² (cm²).

- Biểu thức biểu thị thể tích của hình lập phương có độ dài cạnh là 2x cm là:

(2x)³ = 8x³(cm³).

b) Các biểu thức trên gồm tích của một số với lũy thừa có số mũ nguyên dương của biến x.

Hoạt động 2 trang 47 Toán 7 Tập 2:

a) Viết biểu thức biểu thị:

- Quãng đường ô tô đi được trong thời gian x (h), nếu vận tốc của ô tô là 60 km/h;

- Tổng diện tích của các hình: hình vuông có độ dài cạnh là 2x cm; hình chữ nhật có các kích thước là 3 cm và x cm; hình thoi có độ dài hai đường chéo là 4 cm và 8 cm.

b) Các biểu thức trên có bao nhiêu biến? Mỗi số hạng xuất hiện trong biểu thức có dạng như thế nào?

Lời giải:

a) - Biểu thức biểu thị quãng đường ô tô đi được trong thời gian x (h) với vận tốc 60 km/h là: 60 . x (km).

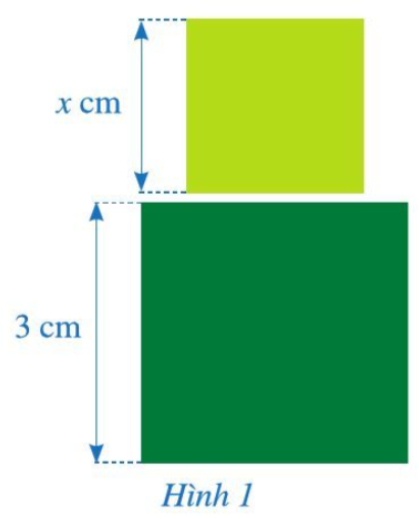
- Biểu thức biểu thị diện tích của hình vuông có độ dài cạnh là 2x cm là: (2x)² = 4x² (cm²).

Biểu thức biểu thị diện tích của hình chữ nhật có các kích thước là 3 cm và x cm là: 3.x (cm²).

Biểu thức biểu thị diện tích của hình thoi có độ dài hai đường chéo là 4 cm và 8 cm là: $\frac{1}{2}\mathrm{.4.8}=16\left(c{m}^2\right)$

Biểu thức biểu thị tổng diện tích của hình vuông có độ dài cạnh là 2x cm; hình chữ nhật có các kích thước là 3 cm và x cm; hình thoi có độ dài hai đường chéo là 4 cm và 8 cm là:

4x² + 3x + 16 (cm²).

b) Các biểu thức trên có một biến x và mỗi số hạng xuất hiện trong biểu thức có dạng là một đơn thức.

Giải Toán 7 trang 48 Tập 2

Luyện tập 1 trang 48 Toán 7 Tập 2:

Biểu thức nào sau đây là đa thức một biến?

a) x² + 9.

b) $\frac{2}{x^2}$ + 2x + 1.

c) 3x + $\frac{2}{5}$y.

Lời giải:

a) Biểu thức x² + 9 là đa thức một biến x.

b) Biểu thức $\frac{2}{x^2}$ + 2x + 1 không là đa thức một biến x vì có chứa lũy thừa của biến ở dưới mẫu.

c) Biểu thức 3x + $\frac{2}{5}$y không là đa thức một biến x vì có chứa biến y.

Hoạt động 3 trang 48 Toán 7 Tập 2:

Cho hai đơn thức của cùng biến x là 2x² và 3x².

a) So sánh số mũ của biến x trong hai đơn thức trên.

b) Thực hiện phép cộng 2x² + 3x².

c) So sánh kết quả của hai phép tính: 2x² + 3x² và (2 + 3)x².

Lời giải:

a) Số mũ của biến x trong đơn thức 2x² bằng 2;

Số mũ của biến x trong đơn thức 3x² bằng 2;

Vậy số mũ của biến x trong hai đơn thức trên bằng nhau.

b) Thực hiện phép cộng:

2x² + 3x² = (x² + x²) + (x² + x² + x²) = x² + x² + x² + x² + x² = 5x².

Vậy 2x² + 3x² = 5x².

c) Ta có: (2 + 3)x² = 5x²

Vậy 2x² + 3x² = (2 + 3)x².

Giải Toán 7 trang 49 Tập 2

Luyện tập 2 trang 49 Toán 7 Tập 2: Thực hiện mỗi phép tính sau:

a) $x^2+\frac{1}{4}{x}^2-5x^2;$

b) $y^4+6y^4-\frac{2}{5}{y}^4;$

Lời giải:

a) Thực hiện phép tính:

$x^2+\frac{1}{4}{x}^2-5x^2=\left(1+\frac{1}{4}-5\right)x^2$

$=\left(\frac{4}{4}+\frac{1}{4}-\frac{20}{4}\right).x^2=\frac{4+1-20}{4}{x}^2=-\frac{15}{4}{x}^2.$

Vậy $x^2+\frac{1}{4}{x}^2-5x^2=-\frac{15}{4}{x}^2.$

b) Thực hiện phép tính:

$y^4+6y^4-\frac{2}{5}{y}^4=\left(1+6-\frac{2}{5}\right).y^4$

$=\left(\frac{5}{5}+\frac{30}{5}-\frac{2}{5}\right).y^4=\frac{5+30-2}{5}{y}^4=\frac{33}{5}{y}^4.$

Vậy $y^4+6y^4-\frac{2}{5}{y}^4=\frac{33}{5}{y}^4.$

Hoạt động 4 trang 49 Toán 7 Tập 2:

Cho đa thức P(x) = x² + 2x² + 6x + 2x - 3.

a) Nêu các đơn thức của biến x có trong đa thức P(x).

b) Tìm số mũ của biến x trong từng đơn thức nói trên.

c) Thực hiện phép cộng các đơn thức có cùng số mũ của biến x sao cho trong đa thức P(x) không còn hai đơn thức nào có cùng số mũ của biến x.

Lời giải:

a) Các đơn thức của biến x có trong đa thức P(x) đã cho là: x²; 2x²; 6x; 2x và ‒3.

b) Số mũ của x trong đơn thức x² bằng 2.

Số mũ của x trong đơn thức 2x² bằng 2.

Số mũ của x trong đơn thức 6x bằng 1.

Số mũ của x trong đơn thức 2x bằng 1.

Số mũ của x trong đơn thức ‒3 bằng 0.

c) Thực hiện phép cộng các đơn thức:

P(x) = x² + 2x² + 6x + 2x - 3

P(x) = (x² + 2x²) + (6x + 2x) - 3

P(x) = (1 + 2)x² + (6 + 2)x – 3

P(x) = 3x² + 8x - 3.

Vậy P(x) = 3x² + 8x - 3.

Luyện tập 3 trang 49 Toán 7 Tập 2: Thu gọn đa thức:

$P\left(y\right)=-2y^3+y+\frac{11}{7}{y}^3+3y^2-5-6y^2+9.$

Lời giải:

$P\left(y\right)=-2y^3+y+\frac{11}{7}{y}^3+3y^2-5-6y^2+9.$

$P\left(y\right)=\left(-2y^3+\frac{11}{7}{y}^3\right)\text{+}\left(3y^2-6y^2\right)+y+\left(-5+9\right)$

$P\left(y\right)=\left(\frac{-14}{7}{y}^3+\frac{11}{7}{y}^3\right)+\left(-3y^2\right)+y+4$

$P\left(y\right)=\left(\frac{-14}{7}+\frac{11}{7}\right)y^3+\left(-3y^2\right)+y+4$

$P\left(y\right)=\frac{-3}{7}{y}^3-3y^2+y+4.$

Vậy $P\left(y\right)=\frac{-3}{7}{y}^3-3y^2+y+4.$

Hoạt động 5 trang 49 Toán 7 Tập 2:

Cho đa thức R(x) = -2x² + 3x² + 6x + 8x⁴ - 1.

a) Thu gọn đa thức R(x).

b) Trong dạng thu gọn của đa thức R(x), sắp xếp các đơn thức theo số mũ giảm dần của biến.

Lời giải:

a) Thu gọn đa thức:

R(x) = -2x² + 3x² + 6x + 8x⁴ - 1

R(x) = (-2x² + 3x²) + 6x + 8x⁴ - 1

R(x) = (-2 + 3).x² + 6x + 8x⁴ - 1

R(x) = x² + 6x + 8x⁴ - 1.

Vậy R(x) = x² + 6x + 8x⁴ - 1.

b) Sắp xếp các đơn thức theo số mũ giảm dần của biến x:

R(x) = x² + 6x + 8x⁴ - 1

R(x) = 8x⁴ + x² + 6x - 1.

Vậy R(x) = 8x⁴ + x² + 6x - 1.

Giải Toán 7 trang 50 Tập 2

Luyện tập 4 trang 50 Toán 7 Tập 2:

Sắp xếp đa thức H(x) = -0,5x⁸ + 4x³ + 5x¹⁰ - 1 theo:

a) Số mũ giảm dần của biến;

b) Số mũ tăng dần của biến.

Lời giải:

a) Sắp xếp đa thức H(x) theo thứ tự số mũ giảm dần của biến x là:

H(x) = -0,5x⁸ + 4x³ + 5x¹⁰ - 1

H(x) = 5x¹⁰ - 0,5x⁸ + 4x³ - 1.

b) Sắp xếp đa thức H(x) theo thứ tự số mũ tăng dần của biến x là:

H(x) = -0,5x⁸ + 4x³ + 5x¹⁰ - 1

H(x) = -1 + 4x³ - 0,5x⁸ + 5x¹⁰.

Hoạt động 6 trang 50 Toán 7 Tập 2:

Cho đa thức P(x) = 9x⁴ + 8x³ - 6x² + x - 1 - 9x⁴.

a) Thu gọn đa thức P(x).

b) Tìm số mũ cao nhất của x trong dạng thu gọn của P(x).

Lời giải:

a) Thu gọn đa thức

P(x) = 9x⁴ + 8x³ - 6x² + x - 1 - 9x⁴

P(x) = (9x⁴ - 9x⁴) + 8x³ - 6x² + x - 1

P(x) = 0x⁴ + 8x³ - 6x² + x - 1

P(x) = 8x³ - 6x² + x - 1.

Vậy P(x) = 8x³ - 6x² + x - 1.

b) Trong dạng thu gọn của P(x) = 8x³ - 6x² + x - 1, ta thấy số mũ cao nhất của x là 3.

Giải Toán 7 trang 51 Tập 2

Luyện tập 5 trang 51 Toán 7 Tập 2:

Cho đa thức R(x) = -1 975x³ + 1 945x⁴ + 2 021x⁵ - 4,5.

a) Sắp xếp đa thức R(x) theo số mũ giảm dần của biến.

b) Tìm bậc của đa thức R(x).

c) Tìm hệ số cao nhất và hệ số tự do của đa thức R(x).

Lời giải:

a) Sắp xếp đa thức R(x) theo số mũ giảm dần của biến:

R(x) = -1 975x³ + 1 945x⁴ + 2 021x⁵ - 4,5

R(x) = 2 021x⁵ + 1 945x⁴ - 1 975x³ - 4,5.

Vậy R(x) = 2 021x⁵ + 1 945x⁴ - 1 975x³ - 4,5.

b) Bậc của đa thức R(x) bằng 5 vì số mũ cao nhất của x trong đa thức Q(x) là 5.

c) Hệ số cao nhất của đa thức R(x) bằng 2021 vì hệ số của lũy thừa với số mũ cao nhất (là 5) của biến là 2021.

Hệ số tự do của đa thức R(x) bằng -4,5 vì đây là số hạng không chứa biến.

Hoạt động 7 trang 51 Toán 7 Tập 2:

a) Tính giá trị của biểu thức đại số 3x - 2 tại x = 2.

b) Tính giá trị của đa thức P(x) = - 4x + 6 tại x = -3.

Lời giải:

a) Thay x = 2 vào biểu thức đại số 3x - 2 ta được 3 . 2 - 2 = 4.

Vậy giá trị của biểu thức đại số 3x - 2 tại x = 2 bằng 4.

b) Thay x = -3 vào đa thức P(x) = - 4x + 6 ta có: P = -4 . (-3) + 6 = 18.

Vậy giá trị của đa thức P(x) = - 4x + 6 tại x = -3 bằng 18.

Hoạt động 8 trang 51 Toán 7 Tập 2:

Cho đa thức P(x) = x² - 3x + 2. Tính P(1), P(2).

Lời giải:

Với đa thức P(x) = x² - 3x + 2 ta có:

P(1) = 1² - 3 . 1 + 2 = 0.

P(2) = 2² - 3 . 2 + 2 = 0.

Vậy P(1) = 0 và P(2) = 0.

Giải Toán 7 trang 52 Tập 2

Vận dụng 6 trang 52 Toán 7 Tập 2:

Trong các phát biểu sau, phát biểu nào đúng, phát biểu nào sai?

a) x = 4 và x = -4 là nghiệm của đa thức P(x) = x² - 16.

b) y = -2 là nghiệm của đa thức Q(y) = -2y³ + 4.

Lời giải:

a) Với đa thức P(x) = x² - 16 ta có:

P(4) = 4² - 16 = 16 – 16 = 0. Do đó x = 4 là nghiệm của đa thức P(x).

P(-4) = (-4)² - 16 = 16 – 16 = 0. Do đó x = -4 là nghiệm của đa thức P(x).

Vậy phát biểu a) là phát biểu đúng.

b) Với đa thức Q(y) = -2y³ + 4 ta có:

Q(-2) = -2 . (-2)³ + 4 = -2 . (-8) + 4 = 16 + 4 = 20.

Do đó y = -2 không là nghiệm của đa thức Q(y).

Vậy phát biểu b) là phát biểu sai.

B. Bài tập

Bài 1 trang 52 Toán 7 Tập 2:

Biểu thức nào sau đây là đa thức một biến? Tìm biến và bậc của đa thức đó.

a) -2x; b) $-x^2-x+\frac{1}{2};$

c) $\frac{4}{x^2+1}+x^2;$ d) $y^2-\frac{3}{y} +1;$

e) - 6z + 8; g) -2t²⁰²¹+ 3t²⁰²⁰ + t - 1.

Lời giải:

a) Biểu thức -2x là đa thức một biến x với bậc bằng 1 (vì 1 là số mũ cao nhất của biến x).

b) Biểu thức $-x^2-x+\frac{1}{2}$ là đa thức một biến x với bậc bằng 2 (vì 2 là số mũ cao nhất của biến x).

c) Biểu thức $\frac{4}{x^2+1}+x^2$ không phải đa thức một biến vì có chứa lũy thừa của biến ở dưới mẫu.

d) Biểu thức $y^2-\frac{3}{y} +1$ không phải đa thức một biến vì có chứa biến y ở dưới mẫu.

e) Biểu thức - 6z + 8 là đa thức một biến z với bậc bằng 1 (vì 1 là số mũ cao nhất của biến z).

g) Biểu thức -2t²⁰²¹ + 3t²⁰²⁰ + t - 1 là đa thức một biến t với bậc bằng 2021 (vì 2021 là số mũ cao nhất của biến t).

Bài 2 trang 52 Toán 7 Tập 2: Thực hiện mỗi phép tính sau:

a) $\frac{4}{9}x+\frac{2}{3}x$;

b) - 12y² + 0,7y²;

c) - 21t³ - 25t³.

Lời giải:

a) $\frac{4}{9}x+\frac{2}{3}x=\left(\frac{4}{9}+\frac{2}{3}\right)x=\left(\frac{4}{9}+\frac{6}{9}\right)x=\frac{10}{9}x;$

b) - 12y² + 0,7y² = (-12 + 0,7)y² = -11,3y².

c) - 21t³ - 25t³ = (-21 - 25)t³ = -46t³.

Bài 3 trang 52 Toán 7 Tập 2: Cho hai đa thức:

P(y) = -12y⁴ + 5y⁴ + 13y³ - 6y³ + y - 1 + 9;

Q(y) = -20y³ + 31y³ + 6y - 8y + y - 7 + 11.

a) Thu gọn mỗi đa thức trên rồi sắp xếp mỗi đa thức theo số mũ giảm dần của biến.

b) Tìm bậc, hệ số cao nhất và hệ số tự do của mỗi đa thức đó.

Lời giải:

a) Thu gọn và sắp xếp đa thức theo số mũ giảm dần của biến:

P(y) = -12y⁴ + 5y⁴ + 13y³ - 6y³ + y - 1 + 9

P(y) = (-12y⁴ + 5y⁴) + (13y³ - 6y³) + y + (-1 + 9)

P(y) = (-12 + 5).y⁴ + (13 - 6).y³ + y + 8

P(y) = -7y⁴ + 7y³ + y + 8.

Q(y) = -20y³ + 31y³ + 6y - 8y + y - 7 + 11

Q(y) = (-20y³ + 31y³) + (6y - 8y + y) + (-7 + 11)

Q(y) = (-20 + 31).y³ + (6 - 8 + 1).y + 4

Q(y) = 11y³ - y + 4.

Vậy P(y) = -7y⁴ + 7y³ + y + 8 và Q(y) = 11y³ - y + 4.

b) Đa thức P(y) = -7y⁴ + 7y³ + y + 8 có bậc bằng 4, hệ số cao nhất bằng -7, hệ số tự do bằng 8.

Đa thức Q(y) = 11y³ - y + 4 có bậc bằng 3, hệ số cao nhất bằng 11, hệ số tự do bằng 4.

Giải Toán 7 trang 53 Tập 2

Bài 4 trang 53 Toán 7 Tập 2:

Cho đa thức P(x) = ax² + bx + c (a ≠ 0). Chứng tỏ rằng:

a) P(0) = c;

b) P(1) = a + b + c;

c) P(-1) = a - b + c.

Lời giải:

Với đa thức P(x) = ax² + bx + c (a ≠ 0) ta có:

a) P(0) = a . 0² + b . 0 + c = 0 + 0 + c = c.

Vậy P(0) = c.

b) P(1) = a . 1² + b . 1 + c = a + b + c.

Vậy P(1) = a + b + c.

c) P(-1) = a . (-1)² + b . (-1) + c = a - b + c.

Vậy P(-1) = a - b + c.

Bài 5 trang 53 Toán 7 Tập 2: Kiểm tra xem:

a) x = 2, $x=\frac{4}{3}$ có là nghiệm của đa thức P(x) = 3x - 4 hay không;

b) y = 1, y = 4 có là nghiệm của đa thức Q(y) = y² - 5y + 4 hay không.

Lời giải:

a) Với đa thức P(x) = 3x - 4 ta có:

P(2) = 3 . 2 - 4 = 6 – 4 = 2. Do đó x = 2 không là nghiệm của đa thức P(x).

$P\left(\frac{4}{3}\right)=3.\frac{4}{3}-4=4-4=0.$ Do đó $x=\frac{4}{3}$ là nghiệm của đa thức P(x).

Vậy x = 2 không là nghiệm của đa thức P(x), $x=\frac{4}{3}$ là nghiệm của đa thức P(x).

b) Với Q(y) = y² - 5y + 4 ta có:

Q(1) = 1² - 5 . 1 + 4 = 1 – 5 + 4 = 0. Do đó y = 1 là nghiệm của đa thức Q(y).

Q(4) = 4² - 5 . 4 + 4 = 16 − 20 + 4 = 0. Do đó y = 4 là nghiệm của đa thức Q(y).

Vậy y = 1, y = 4 là nghiệm của đa thức Q(y).

Bài 6 trang 53 Toán 7 Tập 2:

Theo tiêu chuẩn của Tổ chức Y tế Thế giới (WHO), đối với bé gái, công thức tính cân nặng chuẩn là C = 9 + 2(N - 1) (kg), công thức tính chiều cao chuẩn là H = 75 + 5(N - 1) (cm), trong đó N là số tuổi của bé gái.

(Nguồn: http://sankom.vn)

a) Tính cân nặng chuẩn, chiều cao chuẩn của một bé gái 3 tuổi.

b) Một bé gái 3 tuổi nặng 13,5 kg và cao 86 cm. Bé gái đó có đạt tiêu chuẩn về cân nặng và chiều cao của Tổ chức Y tế Thế giới hay không?

Lời giải:

a) Công thức tính cân nặng chuẩn đối với bé gái là C = 9 + 2(N - 1) (kg) do đó cân nặng chuẩn của bé gái 3 tuổi là: 9 + 2(3 - 1) = 9 + 2 . 2 = 13 (kg).

Công thức tính chiều cao chuẩn đối với bé gái là H = 75 + 5(N - 1) (cm) do đó chiều cao chuẩn của bé gái 3 tuổi là: 75 + 5(3 - 1) = 75 + 5 . 2 = 85 (cm).

b) Ta thấy 13,5 kg > 13 kg và 86 kg > 85 kg nên bé gái đó đạt tiêu chuẩn về cân nặng và chiều cao của Tổ chức Y tế Thế giới.

Bài 7 trang 53 Toán 7 Tập 2:

Nhà bác học Galileo Galilei (1564 - 1642) là người đầu tiên phát hiện ra quãng đường chuyển động của vật rơi tự do tỉ lệ thuận với bình phương của thời gian chuyển động. Quan hệ giữa quãng đường chuyển động y (m) và thời gian chuyển động x (giây) được biểu diễn gần đúng bởi công thức y = 5x². Trong một thí nghiệm vật lí, người ta thả một vật nặng từ độ cao 180 m xuống đất (coi sức cản của không khí không đáng kể).

a) Sau 3 giây thì vật nặng còn cách mặt đất bao nhiêu mét?

b) Khi vật nặng còn cách mặt đất 100 m thì nó đã rơi được thời gian bao lâu?

c) Sau bao lâu thì vật chạm đất?

Lời giải:

a) Sau 3 giây thì vật nặng rơi được 5 . 3² = 45 (m).

Do vật rơi từ độ cao 180 m nên sau 3 giây, vật nặng còn cách mặt đất là:

180 - 45 = 135 (m).

b) Khi vật nặng còn cách mặt đất 100 m thì nó đã rơi được: 180 - 100 = 80 (m).

Tức là 80 = 5x² suy ra x² = 80 : 5 = 16 = 4² = (-4)².

Vì x (giây) là thời gian chuyển động nên x > 0 do đó ta có x = 4.

Vậy vật nặng rơi được 4 giây thì còn cách mặt đấy 100 m.

c) Vật chạm đất tức là vật đã rơi được 180 m.

Khi đó 5x² = 180.

Suy ra x² = 36 = 6² = (-6)².

Do đó x = 6 (do x > 0).

Vậy sau 6 giây rơi thì vật chạm đất.

Bài 8 trang 53 Toán 7 Tập 2:

Pound là một đơn vị đo khối lượng truyền thống của Anh, Mỹ và một số quốc gia khác. Công thức tính khối lượng y (kg) theo x (pound) là: y = 0,45359237x.

a) Tính giá trị của y (kg) khi x = 100 (pound).

b) Một hãng hàng không quốc tế quy định mỗi hành khách được mang hai va li không tính cước; mỗi va li cân nặng không vượt quá 23 kg. Hỏi với va li cân nặng 50,99 pound sau khi quy đổi sang ki - lô - gam và được phép làm tròn đến hàng đơn vị thì có vượt quá quy định trên hay không?

Lời giải:

a) Công thức tính khối lượng y (kg) theo x (pound) là: y = 0,45359237x.

Khi x = 100 (pound) thì y = 0,45359237 . 100 = 45,359237 (kg).

b) Công thức tính khối lượng y (kg) theo x (pound) là: y = 0,45359237x.

Để đổi 50,99 pound sang ki – lô – gam thì ta có:

y = 0,45359237 . 50,99 = 23,12867495 kg ≈ 23 kg.

Vậy va li có cân nặng 50,99 pound không vượt quá quy định.

Lý thuyết Toán 7 Bài 2. Đa thức một biến. Nghiệm của đa thức một biến - Cánh diều

I. Đơn thức một biến. Đa thức một biến

1. Đơn thức một biến

– Đơn thức một biến là biểu thức đại số chỉ gồm một số hoặc một tích của một số với luỹ thừa có số mũ nguyên dương của biến đó.

Chẳng hạn: x², 2x³ là các đơn thức một biến x.

– Chú ý:

+ Mỗi đơn thức (một biến x) nếu không phải là một số thì có dạng ax^k, trong đó a là số thực khác 0 và k là số nguyên dương. Lúc đó, số a được gọi là hệ số của đơn thức ax^k.

+ Để thuận tiện cho việc thực hiện các phép tính (trên các đơn thức, đa thức, …), một số thực khác 0 được coi là đơn thức với số mũ của biến bằng 0.

Ví dụ: Trong các phát biểu sau, phát biểu nào đúng, phát biểu nào sai?

a) x + 1 là đơn thức một biến x;

b) 2x² là đơn thức một biến x;

c) 0 không là đơn thức một biến.

Hướng dẫn giải

a) Sai. Vì đơn thức một biến chỉ gồm một số hoặc một tích của một số với luỹ thừa của biến đó nên x² + 1 không phải là đơn thức một biến mà là đa thức một biến.

b) Đúng. Vì 2x² là tích của 2 với luỹ thừa 2 của biến x nên 2x² là đơn thức một biến x.

c) Sai. Vì một số cũng là đơn thức nên 0 là đơn thức một biến.

2. Đa thức một biến

– Đa thức một biến là tổng những đơn thức của cùng một biến.

Chẳng hạn: 3x² + 2x là đa thức của biến x.

– Chú ý:

+ Mỗi số được xem là một đa thức (một biến).

+ Số 0 được gọi là đa thức không.

+ Mỗi đơn thức cũng là một đa thức.

+ Thông thường ta kí hiệu đa thức một biến x là P(x), Q(x), A(x), B(x), …

Ví dụ: Biểu thức nào sau đây là đa thức một biến x?

a) x² – 9;

b) 2022;

c) 3x + y;

d) $\frac{25}{{\text{x}}^2}$+ 2x + 1.

Hướng dẫn giải

a) x² – 9 là đa thức một biến x vì là hiệu của 2 đơn thức một biến x là x² và 9.

b) 2022 là một số nên cũng được xem là một đa thức một biến.

c) 3x + y không phải là đa thức một biến x vì có cả biến y.

d) $\frac{25}{{\text{x}}^2}$+ 2x + 1 không phải là đa thức một biến x vì $\frac{25}{{\text{x}}^2}$ không phải là tích của một số với luỹ thừa có số mũ nguyên dương của biến x.

II. Cộng trừ đơn thức có cùng số mũ của biến

– Để cộng (trừ) hai đơn thức có cùng số mũ của biến, ta cộng (hay trừ) hai hệ số với nhau và giữ nguyên phần biến:

• ax^k + bx^k = (a + b)x^k;

• ax^k – bx^k = (a – b)x^k (k ∈ ℕ*).

Ví dụ: Thực hiện mỗi phép tính sau:

a) 13x² + 7x²;

b) 4x³ – 3x³;

c) a⁴ + 1,5a⁴ + 0,5a⁴.

Hướng dẫn giải

a) 13x² + 7x² = (13 + 7)x² = 20x²;

b) 4x³ – 3x³ = (4 – 3)x³ = 1.x³ = x³;

c) a⁴ + 1,5a⁴ + 0,5a⁴ = (1 + 1,5 + 0,5)a⁴ = 3a⁴.

III. Sắp xếp đa thức một biến

1. Thu gọn đa thức

Thu gọn đa thức một biến là làm cho đa thức đó không còn hai đơn thức nào có cùng số mũ của biến.

Ví dụ: Thu gọn đa thức:

a) P(x) = 3x² – 4x² + x³ + 3x³ – 4x + x + 1;

b) Q(x) = 2 – 3,5x⁴ – 5x² + 3x² + x + $\frac{7}{2}$x⁴ – 2x³ – 1.

Hướng dẫn giải

a) P(x) = 3x² – 4x² + x³ + 3x³ – 4x + x + 1

= (3 – 4)x² + (1 + 3)x³ + (–4 + 1)x + 1

= –x² + 4x³ – 3x + 1

Vậy dạng thu gọn của đa thức P(x) là –x² + 4x³ – 3x + 1.

b) Q(x) = 2 – 3,5x⁴ – 5x² + 3x² + x + $\frac{7}{2}$x⁴ – 2x³ – 1

= (2 – 1) + (–3,5x⁴ + $\frac{7}{2}$x⁴) + (– 5x² + 3x²) + x – 2x³

= 1 + $\left(-3,5+\frac{7}{2}\right)$x⁴ + (– 5 + 3)x² + x – 2x³

= 1 + 0x⁴ – 2x² + x – 2x³

= 1 – 2x² + x – 2x³

Vậy dạng thu gọn của đa thức Q(x) là 1 – 2x² + x – 2x³.

2. Sắp xếp một đa thức

– Sắp xếp đa thức (một biến) theo số mũ giảm dần (hoặc tăng dần) của biến là sắp xếp các đơn thức trong dạng thu gọn của đa thức đó theo số mũ giảm dần (hoặc tăng dần) của biến.

– Chú ý: Trong dạng thu gọn của đa thức, hệ số của mỗi đơn thức được gọi là hệ số của đa thức đó.

Ví dụ: Sắp xếp đa thức A(x) = 3x² + 5x⁴ – x⁵ + 2x – 1 theo số mũ giảm dần của biến.

Hướng dẫn giải

A(x) = 3x² + 5x⁴ – x⁵ + 2x – 1

= –x⁵ + 5x⁴ + 3x² + 2x – 1.

Vậy sắp xếp đa thức A(x) theo số mũ giảm dần của biến ta được A(x) = –x⁵ + 5x⁴ + 3x² + 2x – 1.

Ví dụ: Cho đa thức P(x) = 3x² + 5x³ – 10x + 2x³ – 8x² + 9 + 6x.

Hãy thu gọn sau đó sắp xếp đa thức theo số mũ giảm dần của biến.

Hướng dẫn giải

P(x) = 3x² + 5x³ – 10x + 2x³ – 8x² + 9 + 6x

= (5x³ + 2x³) + (3x² – 8x²) + (–10x + 6x) + 9

= 7x³ – 5x² – 4x + 9

Vậy P(x) = = 7x³ – 5x² – 4x + 9.

IV. Bậc của đa thức một biến

– Bậc của đa thức một biến (khác đa thức không, đa thu gọn) là số mũ cao nhất của biến trong đa thức đó.

– Chú ý:

+ Trong dạng thu gọn của đa thức, hệ số của luỹ thừa với số mũ cao nhất của biến còn gọi là hệ số cao nhất của đa thức; số hạng không chứa biến còn gọi là hệ số tự do của đa thức.

+ Một số khác 0 là đa thức bậc 0.

+ Đa thức không (số 0) không có bậc.

Ví dụ: Cho đa thức P(x) = x² + 2x² + 6x + 2x – 3.

a) Sắp xếp đa thức P(x) theo số mũ giảm dần của biến;

b) Tìm bậc của đa thức P(x);

c) Tìm hệ số cao nhất và hệ số tự do của đa thức P(x).

Hướng dẫn giải

a) P(x) = x² + 2x² + 6x + 2x – 3

= (x² + 2x²) + (6x + 2x) – 3

= (1 + 2)x² + (6 + 2)x – 3

= 3x² + 8x – 3

Vậy P(x) = 3x² + 8x – 3.

b) Bậc của đa thức P(x) là 2 vì số mũ cao nhất của x trong đa thức P(x) là 2.

c) Đa thức P(x) có hệ số cao nhất là 3 và hệ số tự do là –3.

V. Nghiệm của đa thức một biến

– Giá trị của đa thức P(x) tại x = a được kí hiệu là P(a).

– Nếu tại x = a, đa thức P(x) có giá trị bằng 0 thì a (hoặc x = a) gọi là một nghiệm của đa thức đó.

– Chú ý:

• x = a là nghiệm của đa thức P(x) nếu P(a) = 0.

• Một đa thức (khác đa thức không) có thể có một nghiệm, hai nghiệm, … hoặc không có nghiệm. Số nghiệm của một đa thức không vượt quá bậc của đa thức đó.

Ví dụ: Trong các phát biểu sau, phát biểu nào đúng, phát biểu nào sai?

a) x = 1 là nghiệm của đa thức A(x) = 2x – 2;

b) y = 3 là nghiệm của đa thức B(y) = 4y – 3;

c) z = 1 không là nghiệm của đa thức C(z) = z² + 1.

Hướng dẫn giải

a) Đúng. Vì A(1) = 2.1 – 2 = 0 nên x = 1 là nghiệm của đa thức A(x).

b) Sai. Vì B(3) = 4.3 – 3 = 9 ≠ 0 nên y = 3 không phải là nghiệm của B(y).

c) Đúng. Vì C(1) = 1² + 1 = 2 ≠ 0 nên z = 1 không phải là nghiệm của C(z).

Ví dụ: Cho P(x) = x² – 1. Tìm nghiệm của đa thức P(x).

Hướng dẫn giải

Ta có: P(x) = 0

Suy ra x² – 1 = 0

Do đó x² = 1

Hay x² = 1² = (–1)²

Suy ra x = 1 hoặc x = –1.

Vậy P(x) có nghiệm là x = 1, x = –1.

Xem thêm lời giải bài tập Toán lớp 7 Cánh diều hay, chi tiết khác:

Bài 3: Phép cộng, phép trừ đa thức một biến

Bài 4: Phép nhân đa thức một biến

Bài 5: Phép chia đa thức một biến

Bài tập cuối chương 6

Bài 1: Tổng các góc của một tam giác