Toán 7 Bài 2 (Cánh diều): Cộng, trừ, nhân, chia số hữu tỉ

Mục lục Giải bài tập Toán lớp 7 Bài 2: Cộng, trừ, nhân, chia số hữu tỉ

Bài giảng Toán lớp 7 Bài 2: Cộng, trừ, nhân, chia số hữu tỉ

Hoạt động khởi động

Giải Toán 7 trang 12 Tập 1

Khởi động trang 12 Toán lớp 7 Tập 1: Đèo Hải Vân là một cung đường hiểm trở trên tuyến giao thông suốt Việt Nam. Để thuận lợi cho việc đi lại, người ta đã xây dựng hầm đường bộ xuyên đèo Hải Vân.

Hầm Hải Vân có chiều dài là 6,28 km và bằng $\frac{157}{500}$ độ dài của đèo Hải Vân. Độ dài của đèo Hải Vân là bao nhiêu ki-lô-mét?

Lời giải:

Độ dài của đèo Hải Vân là:

$6,28:\frac{157}{500}=\frac{628}{100}:\frac{157}{500}=\frac{157}{25}.\frac{500}{157}=\frac{500}{25}=\frac{500:25}{25:25}=\frac{20}{1}=20$ (km).

Vậy độ dài của đèo Hải Vân là 20 ki-lô-mét.

1. Cộng, trừ hai số hữu tỉ. Quy tắc chuyển vế

Hoạt động 1 trang 12 Toán lớp 7 Tập 1: Thực hiện các phép tính sau:

a) $\frac{-2}{5}+\frac{3}{7}$;

b) 0,123 – 0,234.

Lời giải:

a) $\frac{-2}{5}+\frac{3}{7}=\frac{\left(-2\right).7}{5.7}+\frac{3.5}{7.5}=\frac{-14}{35}+\frac{15}{35}$

$=\frac{-14+15}{35}=\frac{1}{35}$;

b) 0,123 – 0,234 = – (0,234 – 0,123) = – 0,111.

Luyện tập 1 trang 12 Toán lớp 7 Tập 1: Tính:

a) $\frac{5}{7}-(-\mathrm{3,9})$;

b) $(-\mathrm{3,25})+4\frac{3}{4}$.

Lời giải:

a) $\frac{5}{7}-(-3,9)=\frac{5}{7}+\frac{39}{10}=\frac{5.10}{7.10}+\frac{39.7}{10.7}$

$=\frac{50}{70}+\frac{273}{70}=\frac{323}{70}$;

b) $(-3,25)+4\frac{3}{4}=\frac{-325}{100}+\frac{19}{4}$

$=\frac{\left(-325\right):25}{100:25}+\frac{19}{4}=\frac{-13}{4}+\frac{19}{4}=\frac{6}{4}=\frac{3}{2}$.

Giải Toán 7 trang 13 Tập 1

Hoạt động 2 trang 13 Toán lớp 7 Tập 1: Nêu tính chất phép cộng các số nguyên.

Lời giải:

Phép cộng số nguyên có các tính chất sau:

Với mọi a, b, c ∈ ℤ:

• Tính chất giao hoán: a + b = b + a;

• Kết hợp: (a + b) + c = a + (b + c);

• Cộng với số 0: a + 0 = 0 + a = a;

• Cộng với số đối: Số đối của số nguyên a được ký hiệu là (−a):

a + (−a) = (−a) + a = 0.

Luyện tập 2 trang 13 Toán lớp 7 Tập 1: Tính một cách hợp lí:

a) $(-\mathrm{0,4})+\frac{3}{8}+(-\mathrm{0,6})$;

b) $\frac{4}{5}-\mathrm{1,8}+\mathrm{0,375}+\frac{5}{8}$.

Lời giải:

a) $(-0,4)+\frac{3}{8}+(-0,6)$

$=(-0,4)+(-0,6)+\frac{3}{8}$ (Tính chất giao hoán)

$=\text{[}(-0,4)+(-0,6)\text{]}+\frac{3}{8}$ (Tính chất kết hợp)

= − 1 + 0,375

= − 0,625;

b) $\frac{4}{5}-1,8+0,375+\frac{5}{8}$

= 0,8 – 1,8 + 0,375 + 0,625

= (0,8 – 1,8) + (0,375 + 0,625) (Tính chất kết hợp)

= (– 1) + 1

= 0 (Tính chất cộng với số đối).

Hoạt động 3 trang 13 Toán lớp 7 Tập 1:

a) Tìm số nguyên x, biết: x + 5 = – 3.

b) Trong tập hợp các số nguyên, nêu quy tắc tìm một số hạng của tổng hai số khi biết tổng và số hạng còn lại.

Lời giải:

a) x + 5 = – 3

x = – 3 – 5

x = – (3 + 5)

x = – 8 (thỏa mãn x là số nguyên).

Vậy x = – 8.

b) Trong tập hợp các số nguyên, muốn tìm một số hạng chưa biết ta lấy tổng của hai số trừ đi số hạng đã biết.

Giải Toán 7 trang 14 Tập 1

Luyện tập 3 trang 14 Toán lớp 7 Tập 1: Tính một cách hợp lý:

a) $x-\left(-\frac{7}{9}\right)=\left(-\frac{5}{6}\right)$;

b) $\frac{15}{-4}-x=\mathrm{0,3}$.

Lời giải:

a) $x-\left(-\frac{7}{9}\right)=\left(-\frac{5}{6}\right)$

$x=\left(-\frac{5}{6}\right)+\left(-\frac{7}{9}\right)$

$x=-\left(\frac{5}{6}+\frac{7}{9}\right)$

$x=-\left(\frac{5.3}{6.3}+\frac{7.2}{9.2}\right)$

$x=-\left(\frac{15}{18}+\frac{14}{18}\right)$

$x=-\frac{29}{18}$.

Vậy $x=-\frac{29}{18}$.

b) $\frac{15}{-4}-x=\mathrm{0,3}$

$\frac{15}{-4}-x=\frac{3}{10}$

$x=-\frac{15}{4}-\frac{3}{10}$

$x=\frac{\left(-15\right).5}{4.5}-\frac{3.2}{10.2}$

$x=-\frac{75}{20}-\frac{6}{20}$

$x=-\left(\frac{75}{20}+\frac{6}{20}\right)$

$x=-\frac{81}{20}$.

Vậy $x=-\frac{81}{20}$.

2. Nhân, chia hai số hữu tỉ

Hoạt động 4 trang 14 Toán lớp 7 Tập 1: Thực hiện các phép tính sau:

a) $\frac{1}{8}.\frac{3}{5}$;

b) $\frac{-6}{7}:\left(-\frac{5}{3}\right)$;

c) 0,6 . (− 0,15).

Lời giải:

a) $\frac{1}{8}.\frac{3}{5}=\frac{1.3}{8.5}=\frac{3}{40}$;

b) $\frac{-6}{7}:\left(-\frac{5}{3}\right)=\frac{-6}{7}.\left(-\frac{3}{5}\right)=\frac{6}{7}.\frac{3}{5}=\frac{18}{35}$;

c) 0,6 . (−0,15) = −(0,6 . 0,15) = −0,09.

Luyện tập 4 trang 14 Toán lớp 7 Tập 1: Giải bài toán nêu trong phần mở đầu.

Lời giải:

Độ dài của đèo Hải Vân là:

$6,28:\frac{157}{500}=\frac{628}{100}:\frac{157}{500}=\frac{157}{25}.\frac{500}{157}=\frac{500}{25}=20$ (km).

Vậy độ dài của đèo Hải Vân là 20 ki-lô-mét.

Luyện tập 5 trang 14 Toán lớp 7 Tập 1: Một ô tô đi từ tỉnh A đến tỉnh B. Trong 1 giờ đầu, ô tô đã đi được $\frac{2}{5}$ quãng đường. Hỏi vẫn với vận tốc đó, ô tô phải mất bao lâu để đi hết cả quãng đường AB?

Lời giải:

Thời gian ô tô đi hết quãng đường AB là:

$1:\frac{2}{5}=\frac{5}{2}=2,5$ (giờ)

Vậy với vận tốc đó, ô tô phải mất 2,5 giờ để đi hết quãng đường AB.

Giải Toán 7 trang 15 Tập 1

Hoạt động 5 trang 15 Toán lớp 7 Tập 1: Nêu tính chất phép nhân các số nguyên.

Lời giải:

Với a, b, c ∈ ℤ ta có các tính chất của phép nhân:

• Tính chất giao hoán: a . b = b . a

• Tính chất kết hợp: (a . b) . c = a . (b . c)

• Nhân với số 1: a . 1 = 1 . a = a

• Tính chất phân phối của phép nhân đối với phép cộng:

a . (b + c) = a . b + a . c

• Tính chất phân phối của phép nhân đối với phép trừ:

a . (b – c) = a . b – a . c.

Luyện tập 6 trang 15 Toán lớp 7 Tập 1: Tính một cách hợp lí:

a) $\frac{7}{3}.(-\mathrm{2,5}).\frac{6}{7}$ ;

b) $\mathrm{0,8}.\frac{-2}{9}-\frac{4}{5}.\frac{7}{9}-\mathrm{0,2}$.

Lời giải:

a) $\frac{7}{3}.(-2,5).\frac{6}{7}$

$=\frac{7}{3}.\frac{6}{7}.(-2,5)$ (Tính chất giao hoán)

$=\frac{6}{3}.\frac{-5}{2}$

$=\frac{6.\left(-5\right)}{3.2}=\frac{-30}{6}=-5$.

b) $0,8.\frac{-2}{9}-\frac{4}{5}.\frac{7}{9}-0,2$

$=\frac{4}{5}.\frac{-2}{9}-\frac{4}{5}.\frac{7}{9}-0,2$

$=\frac{4}{5}.\left(\frac{-2}{9}-\frac{7}{9}\right)-0,2$ (Tính chất phân phối của phép nhân đối với phép trừ)

$=\frac{4}{5}.\left(\frac{-9}{9}\right)-0,2$

$=\frac{4}{5}.(-1)-\frac{1}{5}$

$=\frac{-4}{5}-\frac{1}{5}$

$=\frac{\left(-4\right)-1}{5}$

$=\frac{-5}{5}=-1$.

Hoạt động 6 trang 15 Toán lớp 7 Tập 1: Nêu phân số nghịch đảo của phân số $\frac{m}{n}(m\ne \mathrm{0,}n\ne 0)$.

Lời giải:

Với m ≠ 0, n ≠ 0 thì ta có: $\frac{m}{n}.\frac{n}{m}=1.$

Vậy với m ≠ 0, n ≠ 0 thì phân số nghịch đảo của phân số $\frac{m}{n}$ là phân số $\frac{n}{m}.$

Giải Toán 7 trang 16 Tập 1

Luyện tập 7 trang 16 Toán lớp 7 Tập 1: Tìm số nghịch đảo của mỗi số hữu tỉ sau:

a) $2\frac{1}{5}$; b) − 13.

Lời giải:

a) Ta có: $2\frac{1}{5}=\frac{2.5+1}{5}=\frac{11}{5}$.

Vì $\frac{11}{5}$.$\frac{5}{11}$ = 1 nên số nghịch đảo của $\frac{11}{5}$ là $\frac{5}{11}$.

Do đó, số nghịch đảo của $2\frac{1}{5}$ là $\frac{11}{5}$

Vậy số nghịch đảo của số $2\frac{1}{5}$ là $\frac{5}{11}$.

b) Vì (–13).$\left(\frac{-1}{13}\right)$ =1 nên số nghịch đảo của (–13) là $\frac{-1}{13}$.

Vậy số nghịch đảo của số (− 13) là $\frac{-1}{13}$.

Bài tập

Bài 1 trang 16 Toán lớp 7 Tập 1: Tính:

a) $\frac{-1}{6}+\mathrm{0,75}$;

b) $3\frac{1}{10}-\frac{3}{8}$;

c) $\mathrm{0,1}+\frac{-9}{17}-(-\mathrm{0,9})$.

Lời giải:

a) $\frac{-1}{6}+\mathrm{0,75}=\frac{-1}{6}+\frac{3}{4}$

$=\frac{\left(-1\right).2}{6.2}+\frac{3.3}{3.4}=\frac{-2}{12}+\frac{9}{12}=\frac{7}{12}$.

b) $3\frac{1}{10}-\frac{3}{8}=\frac{31}{10}-\frac{3}{8}$

$=\frac{31.4}{10.4}-\frac{3.5}{8.5}=\frac{124}{40}-\frac{15}{40}=\frac{109}{40}$.

c) $\mathrm{0,1}+\frac{-9}{17}-(-\mathrm{0,9})$

$=\mathrm{0,1}+\frac{-9}{17}+\mathrm{0,9}$

$=\mathrm{0,1}+\mathrm{0,9}+\frac{-9}{17}$ (Tính chất giao hoán)

$=1+\frac{-9}{17}$

$=\frac{17}{17}+\frac{-9}{17}$

$=\frac{8}{17}$ .

Bài 2 trang 16 Toán lớp 7 Tập 1: Tính:

a) $\mathrm{5,75}.\frac{-8}{9}$;

b) $2\frac{3}{8}.(-\mathrm{0,4})$;

c) $\frac{-12}{5}:(-\mathrm{6,5})$.

Lời giải:

a) $\mathrm{5,75}.\frac{-8}{9}=\frac{575}{100}.\frac{-8}{9}$

$=\frac{23}{4}.\frac{-8}{9}=\frac{\mathrm{23.4.}\left(-2\right)}{4.9}=\frac{-46}{9}$;

b) $2\frac{3}{8}.(-\mathrm{0,4})=\frac{19}{8}.\frac{-4}{10}$

$=\frac{19.\left(-2\right)}{\left(-4\right).\left(-2\right).5}=\frac{-19}{20}$;

c) $\frac{-12}{5}:(-6,5)=\frac{-12}{5}:\frac{-65}{10}=\frac{12}{5}:\frac{65}{10}$

$=\frac{12}{5}:\frac{13}{2}=\frac{12}{5}.\frac{2}{13}=\frac{24}{65}$.

Bài 3 trang 16 Toán lớp 7 Tập 1: Tính một cách hợp lí:

a) $\frac{-3}{10}-\mathrm{0,125}+\frac{-7}{10}+\mathrm{1,125}$;

b) $\frac{-8}{3}.\frac{2}{11}-\frac{8}{3}:\frac{11}{9}$.

Lời giải:

a) $\frac{-3}{10}-\mathrm{0,125}+\frac{-7}{10}+\mathrm{1,125}$

$=\frac{-3}{10}+\frac{-7}{10}+\mathrm{1,125}-\mathrm{0,125}$ (Tính chất giao hoán)

$=-\left(\frac{3}{10}+\frac{7}{10}\right)+(\mathrm{1,125}-\mathrm{0,125})$ (Tính chất kết hợp)

$=-\frac{10}{10}+1$

= − 1 + 1

= 0. (Tính chất cộng với số đối).

b) $\frac{-8}{3}.\frac{2}{11}-\frac{8}{3}:\frac{11}{9}$

$=-\frac{8}{3}.\frac{2}{11}-\frac{8}{3}.\frac{9}{11}$

$=-\frac{8}{3}.\left(\frac{2}{11}+\frac{9}{11}\right)$

$=-\frac{8}{3}.1$

$=-\frac{8}{3}$ (Tính chất nhân với 1).

Bài 4 trang 16 Toán lớp 7 Tập 1: Tìm x, biết:

a) $x+\left(-\frac{1}{5}\right)=\frac{-4}{15}$;

b) $\mathrm{3,7}-x=\frac{7}{10}$;

c) $x.\frac{3}{2}=\mathrm{2,4}$;

d) $\mathrm{3,2}:x=-\frac{6}{11}$.

Lời giải:

a) $x+\left(-\frac{1}{5}\right)=\frac{-4}{15}$

$x=\frac{-4}{15}-\left(-\frac{1}{5}\right)$

$x=\frac{-4}{15}+\frac{1}{5}$

$x=\frac{-4}{15}+\frac{1.3}{5.3}$

$x=\frac{-4}{15}+\frac{3}{15}$

$x=\frac{-1}{15}$.

Vậy $x=\frac{-1}{15}$.

b) $\mathrm{3,7}-x=\frac{7}{10}$

$\frac{37}{10}$– x = $\frac{7}{10}$

x = $\frac{37}{10}$– $\frac{7}{10}$

x = $\frac{30}{10}$

x = 3.

Vậy x = 3.

c) $x.\frac{3}{2}=\mathrm{2,4}$

x.$\frac{3}{2}=\frac{24}{10}$

x = $\frac{24}{10}:\frac{3}{2}$

$x=\frac{24}{10}.\frac{2}{3}$

$x=\frac{8}{5}$.

Vậy $x=\frac{8}{5}$.

d) $\mathrm{3,2}:x=-\frac{6}{11}$

$\frac{32}{10}:x=-\frac{6}{11}$

$x=\frac{32}{10}:\left(-\frac{6}{11}\right)$

$x=\frac{32}{10}.\left(-\frac{11}{6}\right)$

$x=-\frac{88}{15}$ .

Vậy $x=-\frac{88}{15}$ .

Bài 5 trang 16 Toán lớp 7 Tập 1: Bác Nhi gửi vào ngân hàng 60 triệu đồng với kì hạn 1 năm, lãi suất 6,5%/năm. Hết kì hạn 1 năm, bác rút ra $\frac{1}{3}$ số tiền (kể cả gốc và lãi). Tính số tiền còn lại của bác Nhi trong ngân hàng.

Lời giải:

1 năm = 12 tháng.

Cách tính tiền lãi có kì hạn là:

Số tiền lãi = Số tiền gửi . lãi suất (%/năm) . số tháng gửi : 12.

Số tiền lãi sau một năm là:

60 . 6,5% .$\frac{12}{12}$ = 60 .$\frac{13}{200}$ = 3,9 (triệu đồng)

Số tiền cả gốc lẫn lãi bác Nhi nhận được sau một năm là:

60 + 3,9 = 63,9 (triệu đồng).

Vì khi bác Nhi rút ra $\frac{1}{3}$ số tiền trong ngân hàng thì số tiền còn lại sẽ là $1-\frac{1}{3}=\frac{2}{3}$ số tiền trong ngân hàng.

Số tiền còn lại của bác Nhi trong ngân hàng là:

63,9.$\frac{2}{3}$ = 42,6 (triệu đồng).

Vậy số tiền còn lại của bác Nhi trong ngân hàng là 42,6 triệu đồng.

Bài 6 trang 16 Toán lớp 7 Tập 1: Tính diện tích mặt bằng của ngôi nhà trong hình vẽ bên (các số đo trên hình tính theo đơn vị mét):

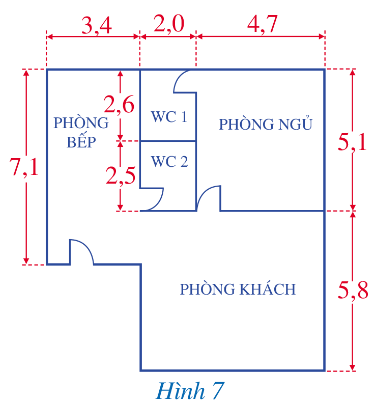
Lời giải:

Diện tích phòng ngủ là:

5,1 . 4,7 = 23,97 (m²)

Diện tích phòng bếp là:

7,1 . 3,4 = 24,14 (m²)

Chiều dài phòng khách là:

2,0 + 4,7 = 6,7 (m)

Diện tích phòng khách là:

6,7 . 5,8 = 38,86 (m²)

Chiều dài phòng vệ sinh là:

2,6 + 2,5 = 5,1 (m)

Diện tích hai phòng vệ sinh là:

5,1 . 2,0 = 10,2 (m²)

Diện tích mặt bằng của ngôi nhà là:

23,97 + 24,14 + 38,86 + 10,2 = 97,17 (m²)

Vậy diện tích mặt bằng của ngôi nhà trong hình vẽ là 97,17 m².

Bài 7 trang 16 Toán lớp 7 Tập 1: Theo yêu cầu của kiến trúc sư, khoảng cách tối thiểu giữa ổ cắm và vòi nước của nhà chú Năm là 60 cm. Trên bản vẽ có tỉ lệ 1 : 20 của thiết kế nhà chú Năm, khoảng cách từ ổ cắm điện đến vòi nước đo được là 2,5 cm. Khoảng cách trên bản vẽ như vậy có phù hợp với yêu cầu của kiến trúc sư không? Giải thích vì sao.

Lời giải:

Theo bản vẽ, khoảng cách thực tế giữa ổ cắm và vòi nước của nhà chú Năm là:

$2,5:\left(1:20\right)=\frac{5}{2}:\frac{1}{20}=\frac{5}{2}.20=50$ (cm) .

Theo yêu cầu của kiến trúc sư, khoảng cách tối thiểu giữa ổ cắm và vòi nước của nhà chú Năm là 60 cm (tức là khoảng cách từ ổ cắm và vòi nước lớn hơn hoặc bằng 60 cm).

Vì 50 < 60 nên khoảng cách thực tế không phù hợp với yêu cầu của kiến trúc sư.

Lý thuyết Toán 7 Bài 2. Cộng, trừ, nhân, chia số hữu tỉ - Cánh diều

1. Cộng, trừ hai số hữu tỉ. Quy tắc chuyển vế

1.1 Quy tắc cộng, trừ hai số hữu tỉ

- Mọi số hữu tỉ đều viết được dưới dạng phân số nên ta có thể cộng, trừ hai số hữu tỉ bằng cách viết chúng dưới dạng phân số rồi áp dụng quy tắc cộng, trừ phân số.

- Nếu hai số hữu tỉ cùng được viết dưới dạng số thập phân (với hữu hạn chữ số khác 0 ở phần thập phân) thì ta có thể cộng, trừ hai số đó theo quy tắc cộng, trừ số thập phân.

Ví dụ: Tính

a) $0,5+\frac{-2}{3}$;

b) 1,205 – 2,31.

Hướng dẫn giải

a) Ta có $0,5=\frac{5}{10}=\frac{1}{2}$ . Do đó:

$0,5+\frac{-2}{3}=\frac{1}{2}+\frac{-2}{3}=\frac{1.3}{2.3}+\frac{(-2).2}{3.2}\text{=}\frac{3}{6}+\frac{-4}{6}=\frac{3+(-4)}{6}=\frac{-1}{6}$.

b) 1,205 – 2,31= 1,205 + (–2,31) = – (2,31 – 1,205) = –1,105.

1.2 Tính chất của phép cộng các số hữu tỉ

- Phép cộng các số hữu tỉ có các tính chất giống với phép cộng các số nguyên: giao hoán, kết hợp, cộng với số 0, cộng với số đối.

- Ta có thể chuyển phép trừ cho một số hữu tỉ thành phép cộng với số đối của số hữu tỉ đó. Vì thế, trong một biểu thức chỉ có phép cộng và phép trừ, ta có thể thay đổi tùy ý vị trí các số hạng kèm theo dấu của chúng.

Ví dụ: Tính một cách hợp lý $(-0,4)+\frac{3}{8}+(-0,6)$

Ta có: $(-0,4)+\frac{3}{8}+(-0,6)=(-0,4)+(-0,6)+\frac{3}{8}=-1+\frac{3}{8}=\frac{-8}{8}+\frac{3}{8}=\frac{-5}{8}$

1.3 Quy tắc chuyển vế

Khi chuyển một số hạng tử vế này sang vế kia của một đẳng thức, ta phải đổi dấu số hạng đó:

x + y = z ⇒ x = z – y

x – y = z ⇒ x = z + y

Ví dụ: Tìm x, biết

a) $x-\left(-\frac{7}{9}\right)=-\frac{5}{6}$;

b) $\frac{15}{-2}-x=0,3$.

Hướng dẫn giải

a) $x-\left(-\frac{7}{9}\right)=-\frac{5}{6}$

$\text{x = }\left(-\frac{5}{6}\right)+\left(-\frac{7}{9}\right)$

$\text{x =}\left(-\frac{15}{18}\right)+\left(-\frac{14}{18}\right)$

$\text{ x = }-\frac{29}{18}$

Vậy $\text{ x = }-\frac{29}{18}$ .

$b) \frac{15}{-2}-x=0,3$

$\frac{15}{-2}-0,3=x$

$\text{ x = }\frac{15}{-2}-0,3$

$\text{x = }-7,8$

Vậy x = – 7,8.

2. Nhân, chia hai số hữu tỉ

2.1 Quy tắc nhân, chia hai số hữu tỉ

- Mọi số hữu tỉ đều viết được dưới dạng phân số nên ta có thể nhân, chia hai số hữu tỉ bằng cách viết chúng dưới dạng phân số rồi áp dụng quy tắc nhân, chia phân số.

- Nếu hai số hữu tỉ cùng viết ở dạng số thập phân (với hữu hạn chữ số khác 0 ở phần thập phân) thì ta có thể nhân, chia hai số đó theo quy tắc nhân, chia số thập phân.

Ví dụ:

a) $2\frac{3}{8}:(-0,4)$ ;

b) $\frac{-12}{5}\cdot (-6,5)$ .

Hướng dẫn giải

a) Ta viết $2\frac{3}{8}=\frac{19}{8}$và $-0,4=\frac{-4}{10}=\frac{-2}{5}$

Khi đó: $2\frac{3}{8}:(-0,4)=\frac{19}{8}:\frac{-2}{5}=\frac{19}{8}\cdot \frac{5}{-2}=\frac{95}{-16}$

b) Ta có thể viết $-\frac{12}{5}=-\frac{24}{10}=-2,4$

Khi đó $\frac{-12}{5}\cdot (-6,5)=(-2,4).(-6,5)=15,6$ .

2.2 Tính chất của phép nhân các số hữu tỉ

Giống như phép nhân các số nguyên, phép nhân các số hữu tỉ có các tính chất: giao hoán, kết hợp, nhân với số 1, phân phối của phép nhân đối với phép cộng và phép trừ.

Ví dụ: Tính một cách hợp lý:

a) $\frac{7}{3}\cdot (-2,5)\cdot \frac{6}{7}$ ;

b) $0,5\cdot \left(\frac{2}{7}+\frac{2}{-3}\right)$ .

Hướng dẫn giải

a) $\frac{7}{3}\cdot (-2,5)\cdot \frac{6}{7}=\frac{7}{3}\cdot \frac{6}{7}\cdot (-2,5)=2\cdot (-2,5)=-5$

b) Ta có $0,5=\frac{5}{10}=\frac{1}{2}$ . Khi đó:

$0,5\cdot \left(\frac{2}{7}+\frac{2}{-3}\right)=\frac{1}{2}\cdot \left(\frac{2}{7}+\frac{2}{-3}\right)=\frac{1}{2}\cdot \frac{2}{7}+\frac{1}{2}\cdot \frac{2}{-3}=\frac{1}{7}+\frac{1}{-3}=\frac{3}{21}+\frac{-7}{21}=\frac{-4}{21}$

Nhận xét:

- Số nghịch đảo của số hữu tỉ a khác 0 kí hiệu là $\frac{1}{a}$ . Ta có $a.\frac{1}{a}=1$

- Số nghịch đảo của số hữu tỉ $\frac{1}{a}$ là a.

- Nếu a, b là hai số hữu tỉ và b ≠ 0 thì $a:b=a\cdot \frac{1}{b}$.

Ví dụ:

Số nghịch đảo của $\frac{-3}{5}$ là $1:\frac{-3}{5}=\frac{5}{-3}=\frac{-5}{3}$

Số nghịch đảo của 0,3 là $1:0,3=1:\frac{3}{10}=\frac{10}{3}$ .

Xem thêm lời giải bài tập Toán lớp 7 Cánh diều hay, chi tiết khác:

Bài 3: Phép tính lũy thừa với số mũ tự nhiên của một số hữu tỉ

Bài 4: Thứ tự thực hiện các phép tính. Quy tắc dấu ngoặc

Bài 5: Biểu diễn thập phân của số hữu tỉ

Bài tập ôn tập chương 1

Bài 1: Số vô tỉ. Căn bậc hai số học