Toán 7 Bài 3 (Cánh diều): Giá trị tuyệt đối của một số thực

Giải bài tập Toán 7 Bài 3: Giá trị tuyệt đối của một số thực

Bài giảng Toán 7 Bài 3: Giá trị tuyệt đối của một số thực

Hoạt động khởi động

Giải Toán 7 trang 44 Tập 1

Khởi động trang 44 Toán lớp 7 Tập 1: Hình 8 mô tả một vật chuyển động từ điểm gốc 0 theo chiều ngược với chiều dương của trục số. Sau 1 giờ, vật đến điểm –40 trên trục số (đơn vị đo trên trục số là ki – lô – mét).

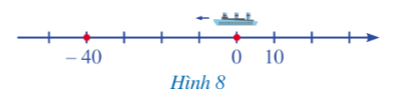
Hỏi khoảng cách từ điểm –40 đến điểm gốc 0 trên trục số là bao nhiêu ki-lô-mét?

Lời giải:

Quan sát Hình 8, ta thấy cứ mỗi đoạn thẳng trên trục số sẽ biểu diễn khoảng cách 10 km.

Do đó khoảng cách từ điểm –40 đến điểm gốc 0 trên trục số là 40 ki-lô-mét.

1. Khái niệm

Hoạt động 1 trang 44 Toán lớp 7 Tập 1:

a) Hãy biểu diễn hai số –5 và 5 trên một trục số.

b) Tính khoảng cách từ điểm 5 đến điểm 0.

c) Tính khoảng cách từ điểm –5 đến điểm 0.

Lời giải:

a) Biểu diễn hai số –5 và 5 trên trục số là:

b) Khoảng cách từ điểm 5 đến điểm 0 là 5 đơn vị.

c) Khoảng cách từ điểm –5 đến điểm 0 là 5 đơn vị.

Giải Toán 7 trang 45 Tập 1

Luyện tập 1 trang 45 Toán lớp 7 Tập 1: So sánh giá trị tuyệt đối của hai số thực a, b trong mỗi trường hợp sau:

Lời giải:

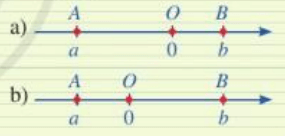
Giá trị tuyệt đối của a là đoạn thẳng OA, giá trị tuyệt đối của b là đoạn thẳng OB.

a) Ở hình a, ta thấy độ dài đoạn OA dài hơn độ dài đoạn thẳng OB

Mà |a| = OA; |b| = OB nên |a| > |b|.

b) Ở hình b, ta thấy độ dài đoạn OA nhỏ hơn độ dài đoạn thẳng OB

Mà |a| = OA; |b| = OB nên |a| < |b|.

2. Tính chất

Hoạt động 2 trang 45 Toán lớp 7 Tập 1: Tìm |x| trong mỗi trường hợp sau:

a) x = 0,5;

b) x = $-\frac{3}{2}$;

c) x = 0;

d) x = –4;

e) x = 4

Lời giải:

a) |x| = |0,5| = 0,5 vì khoảng cách từ điểm 0,5 đến gốc 0 là 0,5.

Vậy |x| = 0,5.

b) |x| = $\left|-\frac{3}{2}\right|=\frac{3}{2}$ vì khoảng cách từ điểm $-\frac{3}{2}$ đến gốc 0 là $\frac{3}{2}$.

Vậy |x| = $\frac{3}{2}$

c) |x| = |0| = 0 vì khoảng cách từ điểm 0 đến gốc 0 là 0.

Vậy |x| = 0.

d) |x| = |–4| = 4 vì khoảng cách từ điểm -4 đến gốc 0 là 4

Vậy |x| = 4.

e) |x| = |4| = 4 vì khoảng cách từ điểm 4 đến gốc 0 là 4.

Vậy |x| = 4.

Giải Toán 7 trang 46 Tập 1

Luyện tập 2 trang 46 Toán lớp 7 Tập 1: Tìm: |–79|; |10,7|; $\left|\sqrt{11}\right|$; $\left|\frac{-5}{9}\right|$.

Lời giải:

|–79| = –(–79) = 79.

|10,7| = 10,7.

$\left|\sqrt{11}\right|$ = $\sqrt{11}$.

$\left|\frac{-5}{9}\right|=-\left(\frac{-5}{9}\right)=-\left(-\frac{5}{9}\right)=\frac{5}{9}.$

Luyện tập 3 trang 46 Toán lớp 7 Tập 1: Cho x = –12. Tính giá trị của mỗi biểu thức sau:

a) 18 + |x|;

b) 25 – |x|;

c) |3 + x | – |7|.

Lời giải:

a) Thay x = –12 vào biểu thức 18 + |x| ta được:

18 + |–12| = 18 + 12 = 30

b) Thay x = –12 vào biểu thức 25 – |x| ta được:

25 – |–12| = 25 – 12 = 13.

c) Thay x = –12 vào biểu thức |3 + x | – |7| ta được:

|3 + (–12)| – |7| = |–9| – |7| = 9 – 7 = 2.

Bài tập

Giải Toán 7 trang 47 Tập 1

Bài 1 trang 47 Toán lớp 7 Tập 1: Tìm: |–59|; $\left|-\frac{3}{7}\right|$; |1,23|; $\left|-\sqrt{7}\right|$.

Lời giải:

Ta có:

|–59| = –(–59) = 59 vì –59 < 0.

$\left|-\frac{3}{7}\right|=-\left(-\frac{3}{7}\right)=\frac{3}{7}$ vì $-\frac{3}{7}<0$.

|1,23| = 1,23 vì 1,23 > 0.

$\left|-\sqrt{7}\right|=-\left(-\sqrt{7}\right)=\sqrt{7}$ vì $-\sqrt{7}<0$.

Bài 2 trang 47 Toán lớp 7 Tập 1: Chọn dấu “<”; “>”; “=” thích hợp cho $\boxed{?}$:

a) $\left|\mathrm{2,3}\right|\boxed{?}\left|-\frac{13}{6}\right|$;

b) $9\boxed{?}\left|-14\right|$;

c) $\left|-\mathrm{7,5}\right|\boxed{?}-\mathrm{7,5}$.

Lời giải:

a) Vì $\left|2,3\right|$ = 2,3 và $\left|\frac{-13}{6}\right|=\frac{13}{6}$

Mà 2,3 > $\frac{13}{6}$ (do $\frac{13}{6}=2,\mathrm{1666...}$).

Do đó, $\left|2,3\right|\boxed{>}\left|\frac{-13}{6}\right|$.

b) Vì |–14| = 14 > 9.

Do đó, $9\boxed{<}\left|-14\right|$.

c) Vì |–7,5| = 7,5 > –7,5.

Do đó, $\left|-7,5\right|\boxed{>}-7,5$.

Bài 3 trang 47 Toán lớp 7 Tập 1: Tính giá trị biểu thức:

a) |–137| + |–363|;

b) |–28| – |98|;

c) (–200) – |–25|.|3|.

Lời giải:

a) |–137| + |–363|

= 137 + 363

= 500;

b) |–28| – |98|

= 28 – 98

= –70;

c) (–200) – |–25|.|3|

= (–200) – 25.3

= (–200) – 75

= –275.

Bài 4 trang 47 Toán lớp 7 Tập 1: Tìm x, biết:

a) |x| = 4;

b) |x| = $\sqrt{7}$;

c) |x + 5| = 0;

d) $\left|x-\sqrt{2}\right|=0$.

Lời giải:

a) |x| = 4 nên x = 4; x = –4.

b) |x| = $\sqrt{7}$ nên x = $\sqrt{7}$; x = –$\sqrt{7}$ .

c) |x + 5| = 0 nên x + 5 = 0 hay x = –5

d) $\left|x-\sqrt{2}\right|=0$ nên $x-\sqrt{2}=0$ hay x = $\sqrt{2}$

Bài 5 trang 47 Toán lớp 7 Tập 1: Trong các phát biểu sau, phát biểu nào đúng, phát biểu nào sai?

a) Giá trị tuyệt đối của một số thực là một số dương.

b) Giá trị tuyệt đối của một số thực là một số không âm.

c) Giá trị tuyệt đối của một số thực là số đối của nó.

d) Hai số đối nhau thì có giá trị tuyệt đối bằng nhau.

Lời giải:

a) Giá trị tuyệt đối của một số thực là một số dương.

Sai vì giá trị tuyệt đối của số 0 là 0 mà 0 không phải là số dương.

b) Giá trị tuyệt đối của một số thực là một số dương.

Đúng vì giá trị tuyệt đối của một số chính là khoảng cách của số đó đến điểm 0 nên nó không thể âm.

c) Giá trị tuyệt đối của một số thực là số đối của nó.

Sai vì 2,5 là số thực và giá trị tuyệt đối của nó là chính nó.

d) Hai số đối nhau thì có giá trị tuyệt đối bằng nhau.

Đúng vì khoảng cách của hai số đó đến 0 là bằng nhau.

Ví dụ: 1,5 và –1,5 là hai số đối nhau nhưng đều có giá trị tuyệt đối là 1,5.

Bài 6 trang 47 Toán lớp 7 Tập 1: So sánh hai số a và b trong mỗi trường hợp sau:

a) a, b là hai số dương và |a| < |b|;

b) a, b là hai số âm và |a| < |b|

Lời giải:

a) Vì a, b là hai số dương nên |a| = a; |b| = b.

Vì |a| < |b| nên a < b.

b) Vì a, b là hai số âm nên |a| = –a; |b| = –b.

Vì |a| < |b| nên –a < –b hay a > b.

Lý thuyết Toán 7 Bài 3. Giá trị tuyệt đối của một số thực – Cánh diều

1. Khái niệm

- Khoảng cách từ điểm x đến điểm gốc 0 trên trục số được gọi là giá trị tuyệt đối của số x, kí hiệu |x|.

Nhận xét:

- Giá trị tuyệt đối của một số luôn là một số không âm: |x| ≥ 0 với mọi số thực x.

- Hai số thực đối nhau có giá trị tuyệt đối bằng nhau.

Ví dụ:

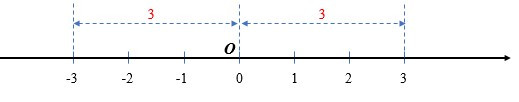
- Khoảng cách từ điểm 3 đến gốc 0 là 3 nên giá trị tuyệt đối của số 3 là 3, tức là |3| = 3.

- Khoảng cách từ điểm –3 đến gốc 0 là 3 nên giá trị tuyệt đối của số –3 là 3, tức là |–3| = 3.

- Số 3 và –3 là hai số đối nhau, |3| = |–3| = 3.

2. Tính chất

- Nếu x là số dương thì giá trị tuyệt đối của x là chính nó: |x| = x (x > 0).

- Nếu x là số âm thì giá trị tuyệt đối của x là số đối của nó: |x| = – x (x < 0).

- Giá trị tuyệt đối của 0 là 0: |0| = 0.

Nhận xét: Với mỗi số thực x, ta có:

+) $\left|\mathrm{x}\right|=\left\{\begin{array}{c}\mathrm{x}\mathrm{khi}\text{ x }\ge \text{0}\\ -\mathrm{x}\text{ khi x < 0}\end{array}\right.$.

+) |– x| = |x|.

Ví dụ: Tìm |– 76| ; |3,1|

Vì – 76 < 0 nên |–76| = – (–76) = 76.

Vì 3,1 > 0 nên |3,1| = 3,1.

Chú ý: Giả sử hai điểm A, B lần lượt biểu diễn hai số thực a, b khác nhau trên trục số. Khi đó, độ dài của đoạn thẳng AB là |a – b|, tức là AB = |a – b|.

Ví dụ: Tính độ dài đoạn thẳng AB trên hình vẽ sau:

a)

Ta có AB = OA + OB = |–3| + |1| = 3 + 1 = 4.

Hay AB = |–3 – 1| = |–4| = 4.

b)

Ta có AB = OA – OB = |–4| – |–1| = 4 – 1 = 3.

Hay AB = |(–4) – (– 1)| = |– 3| = 3.

Xem thêm lời giải bài tập Toán lớp 7 Cánh diều hay, chi tiết khác:

Bài 4: Làm tròn số và ước lượng

Bài 5: Tỉ lệ thức

Bài 6: Dãy tỉ số bằng nhau

Bài 7: Đại lượng tỉ lệ thuận

Bài 8: Đại lượng tỉ lệ nghịch