Toán 7 (Cánh diều) Bài tập cuối chương 2

Giải bài tập Toán 7 Bài tập cuối chương 2

Bài tập

Giải Toán 7 trang 69 Tập 1

Bài 1 trang 69 Toán lớp 7 Tập 1: Tìm những số vô tỉ trong các số sau đây:

–6,123(456); $-\sqrt{4};\sqrt{\frac{4}{9}};\sqrt{11};\sqrt{15}.$

Lời giải:

Ta có:

–6,123(456) là số thập phân vô hạn tuần hoàn nên nó không là số vô tỉ.

$-\sqrt{4}=-2$ là số nguyên âm nên nó không phải số vô tỉ.

$\sqrt{\frac{4}{9}}=\frac{2}{3}$ là phân số nên nó không phải số vô tỉ.

$\sqrt{11}=3,\mathrm{31662479...}$ là số thập phân vô hạn không tuần hoàn nên nó là số vô tỉ.

$\sqrt{15}=3,\mathrm{872983346...}$là số thập phân vô hạn không tuần hoàn nên nó là số vô tỉ.

Vậy số vô tỉ trong các số đã cho là $\sqrt{11};\sqrt{15}.$

Bài 2 trang 69 Toán lớp 7 Tập 1: So sánh:

a) 4,9(18) và 4,928…;

b) –4,315… và –4,318...;

c) $\sqrt{3}$ và $\sqrt{\frac{7}{2}}$.

Lời giải:

a) Ta có:

4,9(18) = 4,918…

Ta so sánh 4,918… và 4,928…

Kể từ trái sang phải, cặp chữ số cùng hàng đầu tiên khác nhau là cặp chữ số hàng phần trăm.

Mà 1 < 2 nên 4,918… < 4,928…

Do đó, 4,9(18) < 4,928…

Vậy 4,9(18) < 4,928…

b) –4,315… và –4,318...

Số đối của –4,315… là 4,315…

Số đối của –4,318... là 4,318...

Ta đi so sánh 4,315… và 4,318…

Kể từ trái sang phải, cặp chữ số cùng hàng đầu tiên khác nhau là cặp chữ số hàng phần nghìn.

Mà 5 < 8 nên 4,315… < 4,318…

Do đó –4,315… > –4,318…

Vậy –4,315… > –4,318…

c) $\sqrt{3}$ và $\sqrt{\frac{7}{2}}$

Ta so sánh 3 và $\frac{7}{2}$.

Ta có $\frac{7}{2}=3,5$.

Vì 0 < 3 < 3,5 nên 0 < 3 < $\frac{7}{2}$.

Do đó, $\sqrt{3}<\sqrt{\frac{7}{2}}$.

Vậy $\sqrt{3}<\sqrt{\frac{7}{2}}$.

Bài 3 trang 69 Toán lớp 7 Tập 1:

a) Sắp xếp các số sau theo thứ tự tăng dần:

6; $\sqrt{35}$; $\sqrt{47}$; –1,7; $-\sqrt{3}$; 0.

b) Sắp xếp các số sau theo thứ tự giảm dần:

$-\sqrt{\mathrm{2,3}};\sqrt{5\frac{1}{6}};0;\sqrt{\mathrm{5,3}};-\sqrt{2\frac{1}{3}};-\mathrm{1,5.}$

Lời giải:

a) 6; $\sqrt{35}$;$\sqrt{47}$; -1,7; $-\sqrt{3}$; 0.

Ta chia thành ba nhóm

Nhóm 1: 6; $\sqrt{35};\sqrt{47}$

Nhóm 2 là 0

Nhóm 3: $-\sqrt{3};-1,7$

• So sánh nhóm 1:

Ta có: 6 = $\sqrt{36}$

Vì 0 < 35 < 36 < 47

Nên $\sqrt{35}<\sqrt{36}<\sqrt{47}$

Hay $\sqrt{35}<6<\sqrt{47}$

Vì 0 luôn nhỏ hơn số dương nên 0 < $\sqrt{35}<6<\sqrt{47}$ (1).

• So sánh nhóm 3: $-1,7=-\sqrt{2,89}$

Vì 2,89 < 3 nên $\sqrt{2,89}<\sqrt{3}$.

Do đó: $-\sqrt{2,89}>-\sqrt{3}$ hay –1,7 > $-\sqrt{3}$.

Vì 0 luôn lớn hơn số âm nên 0 > –1,7 > $-\sqrt{3}$ (2).

Từ (1) và (2) ta sắp xếp theo thứ tự tăng dần như sau:

$-\sqrt{3}$–1,7; 0; $\sqrt{35}$; 6; $\sqrt{47}$

b) $-\sqrt{2,3};\sqrt{5\frac{1}{6}};0;\sqrt{5,3};-\sqrt{2\frac{1}{3}};-1,5.$

Ta chia thành ba nhóm:

Nhóm 1: $\sqrt{5\frac{1}{6}};\sqrt{5,3}$

Nhóm 2 là số 0.

Nhóm 3: $-\sqrt{2,3};-\sqrt{2\frac{1}{3}}$; –1,5.

• So sánh nhóm 1:

$\sqrt{5\frac{1}{6}}=5,\mathrm{166...};\sqrt{5,3}$

Vì 5,3 > 5,166… > 0

Nên $\sqrt{5,3}>\sqrt{5,\mathrm{166...}}$

Hay $\sqrt{5,3}>\sqrt{5\frac{1}{6}}$

Vì 0 luôn nhỏ hơn số dương nên ta có: $\sqrt{5,3}>\sqrt{5\frac{1}{6}}$ > 0 (3)

• So sánh nhóm 3:

–1,5 = –$\sqrt{2,25}$ và $-\sqrt{2\frac{1}{3}}=-\sqrt{2,\mathrm{333...}}$

Vì 2,25 < 2,3 < 2,333…

Nên $\sqrt{2,25}<\sqrt{2,3}<\sqrt{2,\mathrm{333...}}$

Do đó, $-\sqrt{2,25}>-\sqrt{2,3}>-\sqrt{2,\mathrm{333...}}$

Suy ra $-1,5>-\sqrt{2,3}>-\sqrt{2\frac{1}{3}}$

Vì 0 luôn lớn hơn số âm nên 0 > $-1,5>-\sqrt{2,3}>-\sqrt{2\frac{1}{3}}$ (4)

Từ (3) và (4) ta sắp xếp theo thứ tự giảm dần là:

$\sqrt{5,3};\sqrt{5\frac{1}{6}};0;-1,5;-\sqrt{2,3};-\sqrt{2\frac{1}{3}}$

Bài 4 trang 69 Toán lớp 7 Tập 1: Tính:

a) $2.\sqrt{6}.\left(-\sqrt{6}\right)$;

b) $\sqrt{\mathrm{1,44}}-2.{\left(\sqrt{\mathrm{0,6}}\right)}^2$;

c) $\mathrm{0,1.}{\left(\sqrt{7}\right)}^2+\sqrt{\mathrm{1,69}}$;

d) $\left(-\mathrm{0,1}\right).{\left(\sqrt{120}\right)}^2-\frac{1}{4}.{\left(\sqrt{20}\right)}^2$

Lời giải:

a) $2.\sqrt{6}.\left(-\sqrt{6}\right)=-2.\left(\sqrt{6}.\sqrt{6}\right)$

$=-2.\left(\sqrt{6.6}\right)=-2.\left(\sqrt{36}\right)$

$=\left(-2\right).6=-12$

b) $\sqrt{\mathrm{1,44}}-2.{\left(\sqrt{\mathrm{0,6}}\right)}^2$

= $\sqrt{{\mathrm{1,2}}^2}$ – 2.0,6

= 1,2 – 1,2

= 0

c) $\mathrm{0,1.}{\left(\sqrt{7}\right)}^2+\sqrt{\mathrm{1,69}}$

= 0,1.7 + $\sqrt{{\mathrm{1,3}}^2}$

= 0,7 + 1,3 = 2

d) $\left(-\mathrm{0,1}\right).{\left(\sqrt{120}\right)}^2-\frac{1}{4}.{\left(\sqrt{20}\right)}^2$

= (–0,1).120 – $\frac{1}{4}.20$

= –12 – 5

= –17

Bài 5 trang 69 Toán lớp 7 Tập 1: Tìm số x không âm, biết:

a) $\sqrt{x}-16=0$

b) 2$\sqrt{x}=\mathrm{1,5}$

c) $\sqrt{x+4}-\mathrm{0,6}=\mathrm{2,4}$

Lời giải:

a) $\sqrt{x}-16=0$(điều kiện x ≥ 0)

$\sqrt{x}=16$

$\sqrt{x}=\sqrt{{16}^2}$

$\sqrt{x}=\sqrt{256}$

x = 256 (thoả mãn)

Vậy x = 256.

b) 2$\sqrt{x}=\mathrm{1,5}$ (điều kiện x ≥ 0)

$\sqrt{x}$ = 1,5:2

$\sqrt{x}$ = 0,75

$\sqrt{x}=\sqrt{{\mathrm{0,75}}^2}$

$\sqrt{x}= \sqrt{\mathrm{0,5625}}$

x = 0,5625 (thoả mãn)

Vậy x = 0,5625

c)$\sqrt{x+4}-\mathrm{0,6}=\mathrm{2,4}$ (điều kiện x ≥ –4)

$\sqrt{x+4}$ = 2,4 + 0,6

$\sqrt{x+4}$ = 3

$\sqrt{x+4}=\sqrt{3^2}$

$\sqrt{x+4} = \sqrt{9}$

x + 4 = 9

x = 9 – 4

x = 5 (thoả mãn)

Vậy x = 5.

Bài 6 trang 69 Toán lớp 7 Tập 1: Tìm số x trong các tỉ lệ thức sau:

a) $\frac{x}{-3}=\frac{7}{\mathrm{0,75}}$;

b) –0,52 : x = $\sqrt{1,96}:\left(-1,5\right)$;

c) x :$\sqrt{5}=\sqrt{5}:x$.

Lời giải:

a) $\frac{x}{-3}=\frac{7}{0,75}$

Áp dụng tính chất tỉ lệ thức ta có:

0,75.x = (–3).7

0,75.x = –21

x = (–21) : 0,75

x = –28

Vậy x = –28.

b) –0,52 : x = $\sqrt{1,96}:\left(-1,5\right)$

$\frac{-0,52}{x}=\frac{\sqrt{1,96}}{-1,5}$

Áp dụng tính chất tỉ lệ thức ta có:

$\left(-0,52\right).\left(-1,5\right)=x.\sqrt{1,96}$

0,78 = x.$\sqrt{1,4^2}$

0,78 = x.1,4

1,4.x = 0,78

$x=\frac{0,78}{1,4}$

$x=\frac{78}{140}$

$x=\frac{39}{70}$

Vậy $x=\frac{39}{70}.$

c) x : $\sqrt{5}=\sqrt{5}:x$

$\frac{x}{\sqrt{5}}=\frac{\sqrt{5}}{x}$

Áp dụng tính chất tỉ lệ thức ta có:

$x.x=\sqrt{5}.\sqrt{5}$

$x^2={\left(\sqrt{5}\right)}^2$

x² = 5

x² = ${\left(\sqrt{5}\right)}^2={\left(-\sqrt{5}\right)}^2$

$x=\sqrt{5}$ hoặc x = $-\sqrt{5}$

Vậy x = $x=\sqrt{5}$ hoặc x = $-\sqrt{5}$

Bài 7 trang 69 Toán lớp 7 Tập 1: Cho $\frac{a}{b}=\frac{c}{d}$ với b – d ≠ 0, b + 2d ≠ 0. Chứng tỏ rằng: $\frac{a-c}{b-d}=\frac{a+2c}{b+2d}$

Lời giải:

Giả sử $\frac{a}{b}=\frac{c}{d}$ = k (với b – d ≠ 0, b + 2d ≠ 0).

Khi đó: a = k.b; c = kd

$\frac{a-c}{b-d}=\frac{bk-dk}{b-d}=\frac{k\left(b-d\right)}{b-d}=k$ (do b – d ≠ 0) (1)

$\frac{a+2c}{b+2d}=\frac{bk+2dk}{b+2d}=\frac{k\left(b+2d\right)}{b+2dd}=k$ (do b + 2d ≠ 0) (2)

Từ (1) và (2) ta có: $\frac{a-c}{b-d}=\frac{a+2c}{b+2d}=k$

Vậy $\frac{a-c}{b-d}=\frac{a+2c}{b+2d}$

Bài 8 trang 69 Toán lớp 7 Tập 1: Tìm ba số x; y; z, biết $\frac{x}{5}=\frac{y}{7}=\frac{z}{9}$ và x – y + z = $\frac{7}{3}$.

Lời giải:

Ta có: $\frac{x}{5}=\frac{y}{7}=\frac{z}{9}$.

Áp dụng tính chất dãy tỉ sống bằng nhau ta có:

$\frac{x}{5}=\frac{y}{7}=\frac{z}{9}=\frac{x-y+z}{5-7+9}=\frac{\frac{7}{3}}{7}=\frac{1}{3}$.

Ta có:

$\frac{x}{5}=\frac{1}{3}$ nên 3x = 1.5 suy ra $x=\frac{1.5}{3}=\frac{5}{3}$

$\frac{y}{7}=\frac{1}{3}$ nên 3y = 1.7 suy ra $y=\frac{1.7}{3}=\frac{7}{3}$

$\frac{z}{9}=\frac{1}{3}$ nên 3z = 1.9 suy ra $z=\frac{1.9}{3}=\frac{9}{3}=3$

Vậy x = $\frac{5}{3}$; y = $\frac{7}{3}$; z = 3.

Bài 9 trang 69 Toán lớp 7 Tập 1: Lớp 7A có 45 học sinh. Trong đợt sơ kết Học kỳ I, số học sinh có kết quả học tập ở các mức Tốt, Khá, Đạt tỉ lệ với ba số 3; 4; 2. Tính số học sinh có kết quả học tập ở mỗi mức, biết trong lớp không có học sinh nào Chưa đạt.

Lời giải:

Gọi số học sinh ở mức Tốt, Khá, Đạt của lớp 7A lần lượt là x; y; z (x; y; z ∈ ℕ*).

Vì lớp 7A có 45 học sinh nên x + y + z = 45.

Vì số học sinh lớp 7A có kết quả học tập ở mức Tốt, Khá, Đạt tỉ lệ với ba số 3; 4; 2 nên ta có dãy tỉ số bằng nhau:

$\frac{x}{3}=\frac{y}{4}=\frac{z}{2}$

Áp dụng tính chất dãy tỉ số bằng nhau ta có:

$\frac{x}{3}=\frac{y}{4}=\frac{z}{2}=\frac{x+y+z}{3+4+2}=\frac{45}{9}=5$

Ta có:

$\frac{x}{3}=5$ suy ra x = 5.3 = 15 (thoả mãn);

$\frac{y}{4}=5$ suy ra y = 5.4 = 20 (thoả mãn);

$\frac{z}{2}=5$ suy ra z = 5.2 = 10 (thoả mãn).

Vậy số học sinh lớp 7A có kết quả học tập ở mức Tốt, Khá và Đạt lần lượt là 15 học sinh; 20 học sinh và 10 học sinh.

Giải Toán 7 trang 70 Tập 1

Bài 10 trang 70 Toán lớp 7 Tập 1: Chị Phương định mua 3 kg táo với số tiền định trước. Khi vào siêu thị đúng thời điểm khuyến mại nên giá táo được giảm 25%. Hỏi với số tiền đó, chị Phương mua được bao nhiêu ki – lô – gam táo?

Lời giải:

Vì giá táo giảm 25% nên giá táo thực tế chị Phương mua được bằng 100% – 75% giá táo dự định.

Đổi 75% = $\frac{3}{4}$. Do đó giá táo thực tế chị Phương mua bằng $\frac{3}{4}$ giá táo niêm yết.

Gọi số táo chị Phương thực tế mua được là a (a Î ℕ*).

Vì giá táo và số lượng táo mua được tỉ lệ nghịch với nhau nên tỉ số của số kg táo thực tế mua được với số kg táo dự định là $\frac{4}{3}$.

Ta có:

$\frac{a}{3}=\frac{4}{3}$ suy ra $a=\frac{4.3}{3}=4$ (kg)

Vậy chị Phương có thể mua 4 (kg) táo với số tiền dự định.

Bài 11 trang 70 Toán lớp 7 Tập 1: Cứ 15 phút chị Lan chạy được 2,5 km. Hỏi trong 1 giờ chị chạy được bao nhiêu ki – lô – mét? Biết rằng vận tốc chạy của chị Lan là không đổi.

Lời giải:

Đổi 15 phút = $\frac{1}{4}$(giờ)

Gọi a (km) là quãng đường chị Lan đã chạy được, b (h) là thời gian chị Lan chạy trên quãng đường tương ứng (a; b > 0).

Vì quãng đường chạy được và thời gian chạy được là hai đại lượng tỉ lệ thuận với nhau nên theo tính chất tỉ lệ thuận ta có:

$\frac{a_1}{b_1}=\frac{a_2}{b_2}$

Thay $a_1=2,5;b_1=\frac{1}{4};b_2=1$, ta có:

$\frac{2,5}{\frac{1}{4}}=\frac{a_2}{1}$ suy ra $a_2=\frac{2,5.1}{\frac{1}{4}}=10$ (km)

Vậy trong 1 giờ chị Lan chạy được 10 km.

Bài 12 trang 70 Toán lớp 7 Tập 1: Một công nhân trong 30 phút làm được 20 sản phẩm. Hỏi để làm được 50 sản phẩm người đó cần bao nhiêu phút? Biết rằng năng suất làm việc của người đó không đổi.

Lời giải:

Gọi x (sản phẩm), y (h) là số sản phẩm và thời gian làm ra số sản phẩm tương ứng của một người công nhân (x ∈ ℕ*; y > 0).

Vì số sản phẩm và thời gian làm số sản phẩm đó tỉ lệ thuận với nhau nên theo tính chất tỉ lệ thuận ta có:

$\frac{x_1}{y_1}=\frac{x_2}{y_2}$.

Thay x₁ = 20; y₁ = 30; x₂ = 50 ta có:

$\frac{20}{30}=\frac{50}{y_2}$

Suy ra $y_2=\frac{30.50}{20}=75$

Vậy để làm được 50 sản phẩm thì người đó cần 75 phút.

Bài 13 trang 70 Toán lớp 7 Tập 1: Cứ đổi 1 158 000 đồng Việt Nam thì được 50 đô la Mỹ.

(Nguồn: https://portal.vietcombank.com.vn, cập nhật vào 18 giờ 30 phút ngày 07/5/2021)

Để có 750 đô la Mỹ thì cần đổi bao nhiêu đồng Việt Nam?

Lời giải:

Gọi x (đô la) và y (đồng) lần lượt là số tiền đô la Mỹ và số tiền Việt Nam đổi ra tương ứng.

Số tiền đô la Mỹ và số tiền Việt Nam tỉ lệ thuận với nhau nên theo tính chất tỉ lệ thuận ta có:

$\frac{x_1}{y_1}=\frac{x_2}{y_2}$.

Thay x₁ = 50; y₁ = 1 158 000; x₂ = 750 ta được:

$\frac{50}{1\text{ 158 000}}=\frac{750}{y_2}$

Suy ra $y_2=\frac{1\text{ 158 000.750}}{50}=17\text{\hspace{0.17em}370 000}$

Vậy để có 750 đô la Mỹ, ta cần đổi 17 370 000 (đồng) Việt Nam.

Bài 14 trang 70 Toán lớp 7 Tập 1: Trong tháng trước, cứ 6 giờ, dây chuyền làm ra 1 000 sản phẩm. Nhưng trong tháng này, do được cải tiến nên năng suất của dây chuyền bằng 1,2 lần năng suất tháng trước. Hỏi trong tháng này, để làm ra 1 000 sản phẩm như thế thì dây chuyền đó cần bao nhiêu giờ?

Lời giải:

Vì cải tiến kỹ thuật nên năng suất tháng này bằng 1,2 lần năng suất tháng trước hay có thể hiểu là tỉ số của năng suất tháng này so với năng suất tháng trước là $\frac{6}{5}$ (vì 1,2 = $\frac{6}{5}$).

Mà năng suất và thời gian sản suất là hai đại lượng tỉ lệ nghịch với nhau.

Do đó tỉ số thời gian để làm 1000 sản phẩm tháng này và thời gian để làm 1000 sản phẩm tháng trước là $\frac{5}{6}$.

Gọi thời gian để làm 1000 sản phẩm tháng này là x (x > 0)

Ta có: $\frac{x}{6}=\frac{5}{6}$ suy ra $x=\frac{6.5}{6}=5$.

Vậy trong tháng này, để làm ra 1 000 sản phẩm thì dây chuyền đó cần 5 giờ.

Bài 15 trang 70 Toán lớp 7 Tập 1: Đồng trắng là một hợp kim của đồng và nickel. Một hợp kim đồng trắng có khối lượng của đồng và nickel tỉ lệ với 9 và 11. Tính khối lượng đồng và nickel cần dùng để tạo ra 25 kg hợp kim đó.

Lời giải:

Gọi x là khối lượng của đồng có trong 25 kg hợp kim, y là khối lượng của nickel có trong 25 kg hợp kim (x; y > 0)

Vì tổng khối lượng hợp kim là 25 kg nên x + y = 25.

Lại có tỉ lệ khối lượng của đồng và nickel trong hợp kim là 9 và 11 nên ta có: $\frac{x}{9}=\frac{y}{11}$.

Áp dụng tính chất dãy tỉ số bằng nhau ta có: $\frac{x}{9}=\frac{\text{y}}{\text{11}}=\frac{x+y}{9+11}=\frac{25}{20}=\frac{5}{4}$.

Ta có:

$\frac{x}{9}=\frac{5}{4}$ suy ra $x=\frac{5.9}{4}=11,25$

Do đó, khối lượng của đồng có trong 25 kg hợp kim là 11,25 kg.

$\frac{y}{11}=\frac{5}{4}$ suy ra $x=\frac{5.11}{4}=13,75$

Do đó, khối lượng của nickel có trong 25 kg hợp kim là 13,75 kg.

Vậy khối lượng của đồng có trong 25kg hợp kim là 11,25 kg; khối lượng của nickel có trong 25 kg hợp kim là 13,75 kg.

Bài 16 trang 70 Toán lớp 7 Tập 1: Cho ba hình chữ nhật có cùng diện tích. Biết chiều rộng của ba hình chữ nhật tỉ lệ với ba số 1; 2; 3. Tính chiều dài mỗi hình chữ nhật đó, biết tổng chiều dài của ba hình chữ nhật đó là 110 cm.

Lời giải:

Gọi chiều dài của ba hình chữ nhật đó là x; y; z (x; y; z > 0).

Vì tổng chiều dài của ba hình chữ nhật đó là 110cm nên x + y + z = 110.

Vì diện tích hình chữ nhật là tích của chiều dài và chiều rộng mà ba hình chữ nhật này có cùng diện tích nên khi chiều rộng tỉ lệ thuận với 1; 2; 3 thì chiều dài của chúng phải tỉ lệ nghịch với 1; 2; 3. Do đó, x = 2y = 3z

Ta có:

• x = 2y suy ra $\frac{x}{2}=\frac{y}{1}$

Do đó $\frac{x}{2}:3=\frac{y}{1}:3$

Hay $\frac{x}{6}=\frac{y}{3}$ (1)

• x = 3z suy ra $\frac{x}{3}=\frac{z}{1}$

Do đó $\frac{x}{3}:2=\frac{z}{1}:2$

Hay $\frac{x}{6}=\frac{z}{2}$ (2)

Từ (1) và (2) ta có dãy tỉ số bằng nhau:

$\frac{x}{6}=\frac{y}{3}=\frac{z}{2}$.

Áp dụng tính chất dãy tỉ số bằng nhau ta có:

$\frac{x}{6}=\frac{y}{3}=\frac{z}{2}=\frac{x+y+z}{6+3+2}=\frac{110}{11}=10$

Ta có:

• $\frac{x}{6}=10$ nên x = 10.6 = 60.

Do đó chiều dài hình chữ nhật thứ nhất là 60 cm.

• $\frac{y}{3}=10$ nên y = 10.3 = 30.

Do đó chiều dài hình chữ nhật thứ hai là 30 cm.

• $\frac{z}{2}=10$ nên z = 10.2 = 20.

Do đó, chiều dài hình chữ nhật thứ ba là 20 cm.

Vậy chiều dài ba hình chữ nhật lần lượt là 60 cm; 30 cm; 20 cm.

Bài 17 trang 70 Toán lớp 7 Tập 1: Hình 14a mô tả hình dạng của một hộp sữa và lượng sữa chứa trong hộp đó. Hình 14b mô tả hình dạng của hộp sữa đó và lượng sữa chứa trong hộp khi đặt hộp ngược lại. Tính tỉ số của thể tích sữa có trong hộp và thể tích cả hộp.

Lời giải:

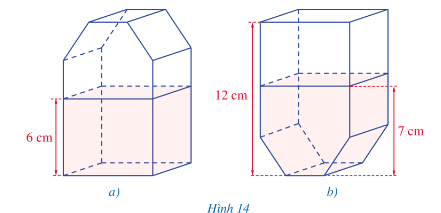
Gọi chiều dài và chiều rộng đáy lớn của hình là x; y (x; y > 0)

Khi đó thể thích sữa của hình a được tính bởi công thức V₁ = 6xy.

Chiều cao của phần không có sữa trên hình b là 12 – 7 = 5 cm.

Thể tích phần không có sữa ở hình b tính bởi công thức V₂ = 5xy.

Vì thể tích sữa ở hai hình như nhau nên thể tích phần không có sữa ở hình b cũng là thể tích phần không có sữa ở hình a.

Do đó, thể tích cả hộp sữa là:

V = V₁ + V₂ = 6xy + 5xy = 11xy.

Tỉ số của thể tích sữa có trong hộp và thể tích cả hộp là:

$\frac{V_1}{V}=\frac{6xy}{11xy}=\frac{6}{11}$

Vậy tỉ số thể tích sữa có trong hộp và thể tích cả hộp là $\frac{6}{11}$.

Lý thuyết Toán 7 Bài tập ôn tập chương 2 – Cánh diều

1. Số vô tỉ

1.1 Khái niệm số vô tỉ

Trong đời sống thực tiễn của con người, ta thường gặp những số không phải là số hữu tỉ. Những số không phải là số hữu tỉ được gọi là số vô tỉ.

1.2 Số thập phân vô hạn không tuần hoàn

Những số thập phân vô hạn mà phần thập phân của nó không có một chu kì nào cả, những số đó được gọi là số thập phân vô hạn không tuần hoàn.

1.3 Biểu diễn thập phân của số vô tỉ

Số vô tỉ được viết dưới dạng số thập phân vô hạn không tuần hoàn.

2. Căn bậc hai số học

- Căn bậc hai số học của một số a không âm là số x không âm sao cho x² = a.

- Căn bậc hai số học của số a (a ≥ 0) được kí hiệu là $\sqrt{\mathrm{a}}$.

- Căn bậc hai số học của số 0 là số 0, viết là: $\sqrt{0}=0$.

Chú ý: Cho a ≥ 0. Khi đó:

+ Đẳng thức $\sqrt{\mathrm{a}}$ = b là đúng nếu b ≥ 0 và b² = a.

+ ${\left(\sqrt{\mathrm{a}}\right)}^2=\mathrm{a}$.

Nhận xét:

- Nếu số nguyên dương a không phải là bình phương của bất kì số nguyên dương nào thì $\sqrt{\mathrm{a}}$ là số vô tỉ.

- Ta có thể tính được giá trị (đúng hoặc gần đúng) căn bậc hai số học của một số dương bằng máy tính cầm tay.

3. Tập hợp số thực

3.1 Số thực

- Số hữu tỉ và số vô tỉ được gọi chung là số thực.

- Tập hợp các số thực được kí hiệu là ℝ.

3.2 Biểu diễn thập phân của số thực

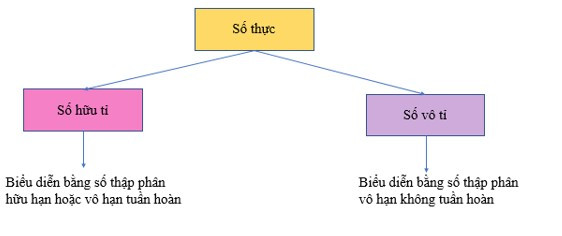
- Mỗi số thực là số hữu tỉ hoặc số vô tỉ. Vì thế, mỗi số thực đều biểu diễn được dưới dạng số thập phân hữu hạn hoặc vô hạn. Ta có sơ đồ sau:

4. Biểu diễn số thực trên trục số

Tương tự như đối với số hữu tỉ, ta có thể biểu diễn mọi số thực trên trục số, khi đó điểm biểu diễn số thực x được gọi là điểm x.

Nhận xét:

- Không phải mỗi điểm trên trục số đều biểu diễn một số hữu tỉ. Vậy các điểm biểu diễn số hữu tỉ không lấp đầy trục số.

- Mỗi số thực được biểu diễn bởi một điểm trên trục số; ngược lại, mỗi điểm trên trục số đều biểu diễn một số thực.

Vậy trục số còn được gọi là trục số thực.

5. Số đối của một số thực

- Trên trục số, hai số thực (phân biệt) có điểm biểu diễn nằm về hai phía của điểm gốc 0 và cách đều điểm gốc 0 được gọi là hai số đối nhau.

- Số đối của số thực a kí hiệu là – a.

- Số đối của số 0 là 0.

Nhận xét: Số đối của – a là số a, tức là –(–a) = a.

6. So sánh các số thực

6.1 So sánh hai số thực

Cũng như số hữu tỉ, trong hai số thực khác nhau luôn có một số nhỏ hơn số kia.

- Nếu số thực a nhỏ hơn số thực b thì ta biết a < b hay b > a.

- Số thực lớn hơn 0 gọi là số thực dương.

- Số thực nhỏ hơn 0 gọi là số thực âm.

- Số 0 không phải là số thực dương cũng không phải số thực âm.

- Nếu a < b và b < c thì a < c.

6.2 Cách so sánh hai số thực

- Ta có thể so sánh hai số thực bằng cách biểu diễn thập phân mỗi số thực đó rồi so sánh hai số thập phân đó.

- Việc biểu diễn một số thực dưới dạng số thập phân (hữu hạn hoặc vô hạn) thường là phức tạp. Trong một số trường hợp ta dùng quy tắc: Với a, b là hai số thực dương, nếu a > b thì $\sqrt{\mathrm{a}}>\sqrt{\mathrm{b}}$.

6.3 Minh họa trên trục số

Giả sử hai điểm x, y lần lượt biểu diễn hai số thực x, y trên trục số nằm ngang. Ta có nhận xét sau:

- Nếu x < y hay y > x thì điểm x nằm bên trái điểm y;

- Ngược lại nếu điểm x nằm bên trái điểm y thì x < y hay y > x.

Đối với hai điểm x, y lần lượt biểu diễn hai số thực x, y trên trục số thẳng đứng, ta cũng có nhận xét sau:

- Nếu x < y hay y > x thì điểm x nằm phía dưới điểm y;

- Ngược lại, nếu điểm x nằm phía dưới điểm y thì x < y hay y > x.

7. Khái niệm giá trị tuyệt đối của số thực

- Khoảng cách từ điểm x đến điểm gốc 0 trên trục số được gọi là giá trị tuyệt đối của số x, kí hiệu |x|.

Nhận xét:

- Giá trị tuyệt đối của một số luôn là một số không âm: |x| ≥ 0 với mọi số thực x.

- Hai số thực đối nhau có giá trị tuyệt đối bằng nhau.

8. Tính chất giá trị tuyệt đối của số thực

- Nếu x là số dương thì giá trị tuyệt đối của x là chính nó: |x| = x (x > 0).

- Nếu x là số âm thì giá trị tuyệt đối của x là số đối của nó: |x| = – x (x < 0).

- Giá trị tuyệt đối của 0 là 0: |0| = 0.

Nhận xét: Với mỗi số thực x, ta có:

+) $\left|\mathrm{x}\right|=\left\{\begin{array}{c}\mathrm{x}\mathrm{khi}\text{ x }\ge \text{0}\\ -\mathrm{x}\text{ khi x < 0}\end{array}\right.$.

+) |– x| = |x|.

Chú ý: Giả sử hai điểm A, B lần lượt biểu diễn hai số thực a, b khác nhau trên trục số. Khi đó, độ dài của đoạn thẳng AB là |a – b|, tức là AB = |a – b|.

9. Làm tròn số

9.1 Số làm tròn

Ở nhiều tình huống thực tiễn ta cần tìm một số thực khác xấp xỉ với số thực đã cho để thuận tiện hơn trong ghi nhớ, đo đạc, hay tính toán. Số thực tìm được như thế được gọi là số làm tròn của số thực đã cho.

9.2 Làm tròn số với độ chính xác cho trước

Ta nói số a được làm tròn đến số b với độ chính xác d nếu khoảng cách giữa điểm a và điểm b trên trục số không vượt quá d.

Nhận xét:

- Khi làm tròn số đến một hàng nào đó thì độ chính xác bằng nửa đơn vị của hàng làm tròn.

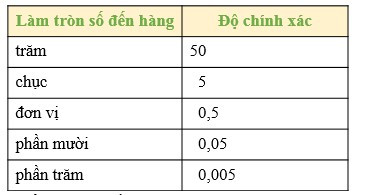
- Để làm tròn số với độ chính xác cho trước, ta có thể sử dụng cách ở bảng sau:

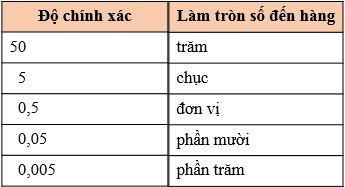
- Để làm tròn một số thập phân âm, ta chỉ cần làm tròn số đối của nó rồi đặt dấu “–” trước kết quả.

Chú ý: Trong đo đạc và tính toán thực tiễn, ta thường có gắng làm tròn số thực với độ chính xác d nhỏ nhất càng tốt. Trong thực tế, làm tròn số thực là một công việc có nhiều khó khăn. Tuy nhiên, người ta cũng biết một số cách để làm tròn số thực.

10. Ước lượng

Trong thực tiễn, đôi lúc ta không quá quan tâm đến tính chính xác của kết quả tính toán mà chỉ cần ước lượng kết quả, tức là tìm một số gần sát với kết quả chính xác.

11. Tỉ lệ thức

Tỉ lệ thức là đẳng thức của hai tỉ số $\frac{\mathrm{a}}{\mathrm{b}}$ và $\frac{\mathrm{c}}{\mathrm{d}}$, viết là $\frac{\mathrm{a}}{\mathrm{b}}=\frac{\mathrm{c}}{\mathrm{d}}$.

Chú ý: Tỉ lệ thức $\frac{\mathrm{a}}{\mathrm{b}}=\frac{\mathrm{c}}{\mathrm{d}}$ còn được viết là a : b = c : d; các số a, b, c, d gọi là các số hạng của tỉ lệ thức.

12. Tính chất của tỉ lệ thức

12.1 Tính chất 1

Nếu $\frac{\mathrm{a}}{\mathrm{b}}=\frac{\mathrm{c}}{\mathrm{d}}$ thì ad = bc.

12.2 Tính chất 2

Nếu ad = bc và a, b, c, d đều khác 0 thì ta có các tỉ lệ thức:

$\frac{\mathrm{a}}{\mathrm{b}}=\frac{\mathrm{c}}{\mathrm{d}}$; $\frac{\mathrm{a}}{\mathrm{c}}=\frac{\mathrm{b}}{\mathrm{d}}$; $\frac{\mathrm{d}}{\mathrm{b}}=\frac{\mathrm{c}}{\mathrm{a}}$; $\frac{\mathrm{d}}{\mathrm{c}}=\frac{\mathrm{b}}{\mathrm{a}}$.

Nhận xét: Với a, b, c, d đều khác 0 thì từ một trong năm đẳng thức sau đây, ta có thể suy ra các đẳng thức còn lại.

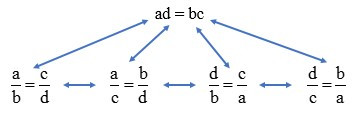
13. Khái niệm dãy tỉ số bằng nhau

Những tỉ số bằng nhau và được viết nối với nhau bởi các dấu đẳng thức tạo thành dãy tỉ số bằng nhau.

Chú ý:

- Với dãy tỉ số bằng nhau $\frac{\mathrm{a}}{\mathrm{b}}=\frac{\mathrm{c}}{\mathrm{d}}=\frac{\mathrm{e}}{\mathrm{g}}$ ta cũng viết a : b = c : d = e : g.

- Khi có dãy tỉ số bằng nhau $\frac{\mathrm{a}}{\mathrm{b}}=\frac{\mathrm{c}}{\mathrm{d}}=\frac{\mathrm{e}}{\mathrm{g}}$, ta nói các số a, c, e tỉ lệ với các số b, d, g và viết là a : c : e = b : d : g.

14. Tính chất dãy tỉ số bằng nhau

Từ tỉ lệ thức $\frac{\mathrm{a}}{\mathrm{b}}=\frac{\mathrm{c}}{\mathrm{d}}$, ta suy ra:

$\frac{\mathrm{a}}{\mathrm{b}}=\frac{\mathrm{c}}{\mathrm{d}}=\frac{\mathrm{a}+\mathrm{c}}{\mathrm{b}+\mathrm{d}}=\frac{\mathrm{a}-\mathrm{c}}{\mathrm{b}-\mathrm{d}}$( b ≠ d và b ≠ –d).

Nhận xét: Tính chất trên còn mở rộng cho dãy tỉ số bằng nhau. Chẳng hạn từ dãy tỉ số bằng nhau $\frac{\mathrm{a}}{\mathrm{b}}=\frac{\mathrm{c}}{\mathrm{d}}=\frac{\mathrm{e}}{\mathrm{g}}$, ta suy ra:

$\frac{\mathrm{a}}{\mathrm{b}}=\frac{\mathrm{c}}{\mathrm{d}}=\frac{\mathrm{e}}{\mathrm{g}}=\frac{\mathrm{a}+\mathrm{c}+\mathrm{e}}{\mathrm{b}+\mathrm{d}+\mathrm{g}}=\frac{\mathrm{a}-\mathrm{c}+\mathrm{e}}{\mathrm{b}-\mathrm{d}+\mathrm{g}}$ (giả thiết các tỉ số đều có nghĩa).

15. Ứng dụng của dãy tỉ số bằng nhau

Các tính chất của dãy tỉ số bằng nhau có nhiều ứng dụng trong thực tiễn, chẳng hạn, ứng dụng vào bài toán chia đại lượng cho trước thành các phần theo tỉ lệ cho trước.

16. Đại lượng tỉ lệ thuận

- Nếu đại lượng y liên hệ với đại lượng x theo công thức y = kx (với k là một hằng số khác 0) thì ta nói y tỉ lệ thuận với x theo hệ số tỉ lệ k.

- Nếu y tỉ lệ thuận với x theo hệ số tỉ lệ k thì x tỉ lệ thuận với y theo hệ số tỉ lệ $\frac{1}{\mathrm{k}}$. Ta nói x và y là hai đại lượng tỉ lệ thuận với nhau.

17. Tính chất của đại lượng tỉ lệ thuận

Nếu hai đại lượng tỉ lệ thuận với nhau thì:

- Tỉ số hai giá trị tương ứng của chúng luôn không đổi;

- Tỉ số hai giá trị bất kì của đại lượng này bằng tỉ số hai giá trị tương ứng của đại lượng kia.

Cụ thể: Giả sử y tỉ lệ thuận với x theo hệ số tỉ lệ k. Với mỗi giá trị x₁, x₂, x₃,… khác 0 của x, ta có một giá trị tương ứng y₁, y₂, y_3­, … của y. Khi đó:

$\frac{{\mathrm{y}}_1}{{\mathrm{x}}_1}=\frac{{\mathrm{y}}_2}{{\mathrm{x}}_2}=\frac{{\mathrm{y}}_3}{{\mathrm{x}}_3}=\mathrm{...}=\mathrm{k};$

$\frac{{\mathrm{x}}_1}{{\mathrm{x}}_2}=\frac{{\mathrm{y}}_1}{{\mathrm{y}}_2};\frac{{\mathrm{x}}_1}{{\mathrm{x}}_3}=\frac{{\mathrm{y}}_1}{{\mathrm{y}}_3};\mathrm{...}$

18. Một số bài toán về đại lượng tỉ lệ thuận

Bài toán 1: Một máy in trong 5 phút in được 120 trang. Hỏi trong 3 phút máy in đó in được bao nhiêu trang?

Hướng dẫn giải

Gọi x (phút), y (trang) lần lượt là thời gian in và số trang mà máy in đã in được. Khi đó mỗi quan hệ giữa thời gian (x) và số trang in được (y) được cho bởi bảng sau:

Ta có thời gian in tỉ lệ thuận với số trang in được theo hệ số tỉ lệ $\mathrm{k}=\frac{120}{5}=24$.

Suy ra $\frac{{\mathrm{y}}_2}{3}=24$. Vì thế y₂ = 24 . 3 = 72.

Vậy trong 3 phút máy in in được 72 trang.

Bài toán 2: Hai thanh chì có thể tích là 12 cm³ và 17 cm³. Hỏi mỗi thanh nặng bao nhiêu gam, biết rằng thanh thứ hai nặng hơn thanh thứ nhất 56,5 g?

Hướng dẫn giải

Gọi khối lượng của hai thanh chì tương ứng là m₁ gam và m₂ gam. Khi đó m₂ – m₁ = 56,5 (g)

Do khối lượng và thể tích của vật thể là hai đại lượng tỉ lệ thuận với nhau. Do đó, ta có:

$\frac{{\mathrm{m}}_1}{12}=\frac{{\mathrm{m}}_2}{17}$.

Áp dụng tính chất dãy tỉ số bằng nhau, ta có: $\frac{{\mathrm{m}}_1}{12}=\frac{{\mathrm{m}}_2}{17}=\frac{{\mathrm{m}}_2-{\mathrm{m}}_1}{17-12}=\frac{56,5}{5}=11,3$.

Suy ra m₁ = 12 . 11,3 = 135,6 ; m₂ = 17 . 11,3 = 192,1.

Vậy hai thanh chì có khối lượng là 135,6 gam và 192,1 gam.

19. Đại lượng tỉ lệ nghịch

- Nếu đại lượng y liên hệ với đại lượng x theo công thức $\mathrm{y}=\frac{\mathrm{a}}{\mathrm{x}}$ hay xy = a (với a là một hằng số khác 0) thì ta nói y tỉ lệ nghịch với x theo hệ số tỉ lệ a.

- Nếu y tỉ lệ nghịch với x theo hệ số tỉ lệ a thì x cũng tỉ lệ nghịch với y theo hệ số tỉ lệ a. Ta nói x và y là hai đại lượng tỉ lệ nghịch với nhau.

Ví dụ: Nếu $\mathrm{y}=\frac{-5}{\mathrm{x}}$ thì ta nói y tỉ lệ nghịch với x theo hệ số tỉ lệ –5. Khi đó x cũng tỉ lệ nghịch với y theo hệ số tỉ lệ –5.

20. Tính chất của đại lượng tỉ lệ nghịch

Nếu hai đại lượng tỉ lệ nghịch với nhau thì:

- Tích hai giá trị tương ứng của chúng luôn không đổi (bằng hệ số tỉ lệ).

- Tỉ số hai giá trị bất kì của đại lượng này bằng nghịch đảo của tỉ lệ hai giá trị tương ứng của đại lượng kia.

Giả sử y tỉ lệ nghịch với x theo hệ số tỉ lệ a. Với mỗi giá trị x₁, x₂, x₃, … khác 0 của x, ta có một giá trị tương ứng y₁, y₂, y₃,… của y. Khi đó:

x₁ y₁ = x₂ y₂ = x₃ y₃ = …= a hay $\frac{{\mathrm{x}}_1}{\frac{1}{{\mathrm{y}}_1}}=\frac{{\mathrm{x}}_2}{\frac{1}{{\mathrm{y}}_2}}=\frac{{\mathrm{x}}_3}{\frac{1}{{\mathrm{y}}_3}}=\mathrm{...}=\mathrm{a};$

$\frac{{\mathrm{x}}_1}{{\mathrm{x}}_2}=\frac{{\mathrm{y}}_2}{{\mathrm{y}}_1};\frac{{\mathrm{x}}_1}{{\mathrm{x}}_3}=\frac{{\mathrm{y}}_3}{{\mathrm{y}}_1};\mathrm{...}$

21. Một số bài toán về đại lượng tỉ lệ nghịch

Chú ý:

- Năng suất lao động và thời gian hoàn thành công việc là hai đại lượng tỉ lệ nghịch.

- Số công nhân và thời gian hoàn thành công việc là hai đại lượng tỉ lệ nghịch.

Bài toán 1: Cho biết 35 công nhân xây một ngôi nhà hết 168 ngày. Hỏi nếu chỉ có 28 công nhân xây ngôi nhà đó thì hết bao nhiêu ngày (giả sử năng suất làm việc của mỗi công nhân là như nhau).

Hướng dẫn giải

Gọi x (công nhân), y (ngày) lần lượt là số công nhân và thời gian xây xong ngôi nhà. Khi đó, mối quan hệ giữa số công nhân (x) và thời gian xây xong ngôi nhà (y) được cho bởi bảng:

Ta có thời gian xây xong nhà (y) tỉ lệ nghịch với số công nhân làm việc theo hệ số tỉ lệ

a = x₁ . y₁ = 35 . 168 = 5 880.

Suy ra 28 . y₂ = 5 880. Vì thế y₂ = 5 880 : 28 = 210 (ngày)

Vậy 28 công nhân xây xong ngôi nhà trong 210 ngày.

Bài toán 2: Để tổ chức liên hoan cho gia đình, bác Ngọc dự định mua 2,9 kg thực phẩm gồm: thịt bò, thịt lợn, tôm sú. Số tiền bác Ngọc mua mỗi loại thực phẩm là như nhau. Biết giá thịt bò là 280 nghìn đồng/kg, giá thịt lợn là 160 nghìn đồng/kg và tôm sú là 320 nghìn đồng/kg. Mỗi loại thực phẩm bác Ngọc mua được là bao nhiêu kg?

Hướng dẫn giải

Gọi x (kg), y (kg), z (kg) lần lượt là số lượng thịt bò, thịt lợn, tôm sú mà bác Ngọc mua được. Khi đó: x + y + z = 2,9.

Vì số tiền mua mỗi loại thực phẩm là như nhau nên 280 . x = 160 . y = 320 . z

hay 7 . x = 4 . y = 8 . z (chia đồng thời các vế cho 40).

Do đó : $\frac{\mathrm{x}}{\frac{1}{7}}=\frac{\mathrm{y}}{\frac{1}{4}}=\frac{\mathrm{z}}{\frac{1}{8}}$.

Áp dụng tính chất của dãy tỉ số bằng nhau ta có:

$\frac{\mathrm{x}}{\frac{1}{7}}=\frac{\mathrm{y}}{\frac{1}{4}}=\frac{\mathrm{z}}{\frac{1}{8}}=\frac{\mathrm{x}+\mathrm{y}+\mathrm{z}}{\frac{1}{7}+\frac{1}{4}+\frac{1}{8}}=\frac{2,9}{\frac{29}{56}}=5,6$.

Do đó:

$\mathrm{x}=5,6\cdot \frac{1}{7}=0,8$ (kg).

$\mathrm{y}=5,6\cdot \frac{1}{4}=1,4$ (kg).

$\mathrm{z}=5,6\cdot \frac{1}{8}=0,7$ (kg).

Vậy Bác Ngọc mua 0,8 kg thịt bò, 1,4 kg thịt lợn và 0,7 kg tôm sú.

Xem thêm lời giải bài tập Toán lớp 7 Cánh diều hay, chi tiết khác:

Bài 1: Hình hộp chữ nhật. Hình lập phương

Bài 2: Hình lăng trụ đứng tam giác. Hình lăng trụ đứng tứ giác

Bài tập ôn tập chương 3

Bài 1: Góc ở vị trí đặc biệt

Bài 2: Tia phân giác của một góc