Toán 7 Bài 1 (Cánh diều): Số vô tỉ. Căn bậc hai số học

Mục lục Giải bài tập Toán 7 Bài 1: Số vô tỉ. Căn bậc hai số học

Bài giảng Toán 7 Bài 1: Số vô tỉ. Căn bậc hai số học

1. Số vô tỉ

Giải Toán 7 trang 33 Tập 1

Hoạt động 1 trang 33 Toán lớp 7 Tập 1: Viết số hữu tỉ $\frac{1}{3}$ dưới dạng số thập phân vô hạn tuần hoàn.

Lời giải:

Ta có:

Vậy số hữu tỉ $\frac{1}{3}$ có thể viết dưới dạng số thập phân vô hạn tuần hoàn là 0, 3333… = 0, (3).

Luyện tập 1 trang 33 Toán lớp 7 Tập 1: Khẳng định “Mỗi số vô tỉ đều không thể là số hữu tỉ” là đúng hay sai? Vì sao?

Lời giải:

Phát biểu trên là đúng vì:

• Mỗi số vô tỉ đều được viết dưới dạng số thập phân vô hạn không tuần hoàn;

• Mỗi số hữu tỉ được viết dưới dạng các số thập phân hữu hạn hoặc vô hạn tuần hoàn

Vậy mỗi số là vô tỉ đều không thể là số hữu tỉ.

2. Căn bậc hai số học

Hoạt động 2 trang 33 Toán lớp 7 Tập 1: Tính:

a) 3²

b) (0,4)²

Lời giải:

a) 3² = 3 . 3 = 9.

b) (0,4)² = 0,4 . 0,4 = 0,16.

Giải Toán 7 trang 34 Tập 1

Luyện tập 2 trang 34 Toán lớp 7 Tập 1: Tính giá trị của:

a) $\sqrt{1600}$

b) $\sqrt{0,16}$

c) $\sqrt{2\frac{1}{4}}$

Lời giải:

Ta có:

a) $\sqrt{1600}$ = $\sqrt{{40}^2}=40$

b) $\sqrt{0,16}$ = $\sqrt{{\mathrm{0,4}}^2}=\mathrm{0,4}$

c) $\sqrt{2\frac{1}{4}}$= $\sqrt{\frac{9}{4}}=\sqrt{{\left(\frac{3}{2}\right)}^2}=\frac{3}{2}$

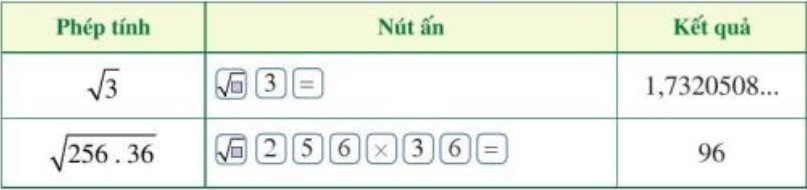
Hoạt động 3 trang 34 Toán lớp 7 Tập 1: Ta có thể tính được giá trị (đúng hoặc gần đúng) căn bậc hai số học của một số dương bằng máy tính cầm tay. Chẳng hạn, để tính $\sqrt{3};\sqrt{256.36}$, ta sử dụng nút dấu căn bậc hai số học $\boxed{\sqrt{}}$ và làm như sau:

Bài tập

Giải Toán 7 trang 35 Tập 1

Bài 1 trang 35 Toán lớp 7 Tập 1:

a) Đọc các số sau: $\sqrt{15};\sqrt{\mathrm{27,6}};\sqrt{\mathrm{0,82}}$.

b) Viết các số sau: Căn bậc hai số học của 39; căn bậc hai số học của $\frac{9}{11}$; căn bậc hai số học của $\frac{89}{27}$.

Lời giải:

a)

$\sqrt{15}$: Căn bậc hai số học của mười lăm.

$\sqrt{27,6}$: Căn bậc hai số học của hai mươi bảy phẩy sáu.

$\sqrt{0,82}$: Căn bậc hai số học của không phẩy tám mươi hai.

b)

Căn bậc hai số học của 39 được viết là $\sqrt{39}$.

Căn bậc hai số học của $\frac{9}{11}$ được viết là $\sqrt{\frac{9}{11}}$

Căn bậc hai số học của $\frac{89}{27}$ được viết là $\sqrt{\frac{89}{27}}$

Bài 2 trang 35 Toán lớp 7 Tập 1: Chứng tỏ rằng:

a) Số 0,8 là căn bậc hai số học của 0,64;

b) Số –11 không phải căn bậc hai số học của 121.

c) Số 1,4 là căn bậc hai số học của 1,96 nhưng –1,4 không phải căn bậc hai số học của 1,96.

Lời giải:

a) Ta có: (0,8)² = 0,8.0,8 = 0,64 và 0,8 > 0 nên số 0,8 là căn bậc hai số học của số 0,64.

b) Ta có: (–11)² = (–11).(–11) = 121 nhưng –11 < 0 nên số –11 không là căn bậc hai số học của số 121.

c) Ta có: (1,4)² = 1,4.1,4 = 1,96 và 1,4 > 0 nên số 1,4 là căn bậc hai số học của số 1,96.

(–1,4)² = (–1,4).(–1,4) = 1,96 nhưng –1,4 < 0 nên số –1,4 không là căn bậc hai số học của số 1,96.

Bài 3 trang 35 Toán lớp 7 Tập 1: Tìm số thích hợp cho $\boxed{?}$:

Lời giải:

+) Ta có: 144 = 12² và 12 > 0 nên $\sqrt{x}=\sqrt{144}$=12.

+) Ta có: 1,69 = 1,3² và 1,3 > 0 nên $\sqrt{x}=\sqrt{1,69}$ = 1,3.

+) Ta có: 14² = 14.14 = 196 nên x = 196.

+) Ta có: 0,1² = 0,1.0,1 = 0,01 nên x = 0,01.

+) Ta có: ${\left(\frac{1}{3}\right)}^2=\frac{1}{3}.\frac{1}{3}=\frac{1}{9}$ nên x = $\frac{1}{9}$.

+) Ta có: 2,25 = 1,5² và 1,5 > 0 nên $\sqrt{x}=\sqrt{2,25}=1,5$.

+) Ta có: 0,0225 = 0,15² và 0,15 > 0 nên $\sqrt{x}=\sqrt{0,0225}=0,15$.

Ta có bảng sau:

Bài 4 trang 35 Toán lớp 7 Tập 1: Tính giá trị của biểu thức:

a) $\sqrt{\mathrm{0,49}}+\sqrt{\mathrm{0,64}}$;

b) $\sqrt{\mathrm{0,36}}-\sqrt{\mathrm{0,81}}$;

c) $8.\sqrt{9}-\sqrt{64}$

d) $0,1.\sqrt{400}+\mathrm{0,2.}\sqrt{1600}$

Lời giải:

a)$\sqrt{\mathrm{0,49}}+\sqrt{\mathrm{0,64}}=\sqrt{{\mathrm{0,7}}^2}+\sqrt{{\mathrm{0,8}}^2}=\mathrm{0,7}+\mathrm{0,8}=\mathrm{1,5}$.

b) $\sqrt{\mathrm{0,36}}-\sqrt{\mathrm{0,81}}=\sqrt{{\mathrm{0,6}}^2}-\sqrt{{\mathrm{0,9}}^2}=\mathrm{0,6}-\mathrm{0,9}=-\mathrm{0,3}$

c) $8.\sqrt{9}-\sqrt{64}=8.\sqrt{3^2}-\sqrt{8^2}=8.3-8=24-8=16$

d) 0,1.$\sqrt{400}+0,2.\sqrt{1600}$

$=0,1.\sqrt{{20}^2}+0,2.\sqrt{{40}^2}$

= 0,1. 20 + 0,2.40

= 2 + 8 = 10.

Bài 5 trang 35 Toán lớp 7 Tập 1: Quan sát Hình 1, ở đó hình vuông AEBF có cạnh bằng 1 dm, hình vuông ABCD có cạnh AB là một đường chéo của hình vuông AEBF.

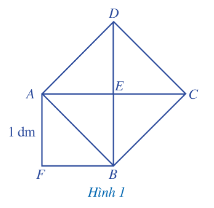
a) Tình diện tích của hình vuông ABCD.

b) Tính độ dài đường chéo AB.

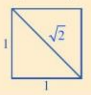
Lưu ý: $\sqrt{2}$ là độ dài đường chéo của hình vuông có cạnh bằng 1.

Lời giải:

a) Ta thấy diện hình vuông ABCD được tạo thành từ 4 tam giác nhỏ có diện tích bằng diện tích tam giác AEB.

Mà hình vuông AEBF là hình vuông có cạnh bằng 1 và tạo bởi hai tam giác là AEB và AFB.

Diện tích hình vuông AEBF là: 1.1 = 1 (dm²).

Diện tích tam giác AEB là: 1 : 2 = $\frac{1}{2}$ (dm²).

Diện tích hình vuông ABCD là: $\frac{1}{2}.4=2$ (dm²).

Vậy diện tích hình vuông ABCD là 2 dm².

b) Vì $\sqrt{2}$ là độ dài đường chéo của hình vuông có độ dài cạnh bằng 1 dm nên độ dài đường chéo AB là $\sqrt{2}$ dm.

Vậy độ dài đường chéo AB là $\sqrt{2}$dm.

Lý thuyết Toán 7 Bài 1. Số vô tỉ. Căn bậc hai số học – Cánh diều

1. Số vô tỉ

1.1 Khái niệm số vô tỉ

Trong đời sống thực tiễn của con người, ta thường gặp những số không phải là số hữu tỉ. Những số không phải là số hữu tỉ được gọi là số vô tỉ.

Ví dụ: Số Pi (π) là tỉ số giữa độ dài của một đường tròn với độ dài đường kính của đường tròn đó và là một số vô tỉ.

1.2 Số thập phân vô hạn không tuần hoàn

Những số thập phân vô hạn mà phần thập phân của nó không có một chu kì nào cả, những số đó được gọi là số thập phân vô hạn không tuần hoàn.

Ví dụ:

Số –1,359130000110578… là số thập phân vô hạn không tuần hoàn.

Số π = 3,14159265358979323846264338… là số thập phân vô hạn không tuần hoàn.

1.3 Biểu diễn thập phân của số vô tỉ

Số vô tỉ được viết dưới dạng số thập phân vô hạn không tuần hoàn.

Ví dụ:

Số –1,359130000110578… là số vô tỉ.

Số π = 3,14159265358979323846264338… là số vô tỉ.

- Nếu a là một số tự nhiên, số nguyên hay số hữu tỉ thì a không thể là số vô tỉ.

2. Căn bậc hai số học

- Căn bậc hai số học của một số a không âm là số x không âm sao cho x² = a.

- Căn bậc hai số học của số a (a ≥ 0) được kí hiệu là $\sqrt{\mathrm{a}}$.

- Căn bậc hai số học của số 0 là số 0, viết là: $\sqrt{0}=0$.

Chú ý: Cho a ≥ 0. Khi đó:

+ Đẳng thức $\sqrt{\mathrm{a}}$ = b là đúng nếu b ≥ 0 và b² = a.

+ ${\left(\sqrt{\mathrm{a}}\right)}^2=\mathrm{a}$.

Ví dụ:

- Ta có 9 > 0 và 9² = 81 nên 9 là căn bậc hai số học của 81. Ta viết: $\sqrt{81}=9$.

- Ta có 0,4 ≥ 0 và (0,4)² = 0,16 nên 0,4 là căn bậc hai số học của 0,16.

Ta viết $\sqrt{0,16}=0,4$.

- Ta có (– 5)² = 25 nhưng – 5 < 0 nên – 5 không phải căn bậc hai số học của số 25.

Nhận xét:

- Nếu số nguyên dương a không phải là bình phương của bất kì số nguyên dương nào thì $\sqrt{\mathrm{a}}$ là số vô tỉ.

Ví dụ: $\sqrt{2};\sqrt{3};\sqrt{5};\sqrt{6};\sqrt{7};\mathrm{...}$ đều là các số vô tỉ.

- Ta có thể tính được giá trị (đúng hoặc gần đúng) căn bậc hai số học của một số dương bằng máy tính cầm tay.

Ví dụ: Để tính $\sqrt{3}$ và $\sqrt{256.36}$ bằng máy tính cầm tay ta làm như sau:

B. Bài tập tự luyện

B.1 Bài tập tự luận

Bài 1. Chứng tỏ rằng:

a) 12 là căn bậc hai số học của 144.

b) – 0,2 không phải là căn số học của 0,04.

Hướng dẫn giải

a) Ta có 12 ≥ 0 và 12² = 144 nên 12 là căn bậc hai số học của 144, ta viết $\sqrt{144}=12$.

b) Ta có (– 0,2)² = 0,04 nhưng – 0,2 < 0 nên – 0,2 không phải là căn bậc hai số học của 0,04.

Bài 2. Tìm giá trị của:

a) $\sqrt{\frac{1}{81}}$ ;

b) $\sqrt{0,49}$.

Hướng dẫn giải

a) $\sqrt{\frac{1}{81}}=\frac{1}{9}$ (vì ${\left(\frac{1}{9}\right)}^2=\frac{1}{81}$).

b) $\sqrt{0,49}=0,7$ (vì (0,7)² = 0,49).

Bài 3. Tính giá trị của biểu thức

a) $\sqrt{0,81}+\sqrt{49}$ ;

b) $0,2.\sqrt{4}-0,1.\sqrt{100}$.

Hướng dẫn giải

a) Ta có $\sqrt{0,81}=0,9$ và $\sqrt{49}=7$.

Nên $\sqrt{0,81}+\sqrt{49}=0,9+7=7,9$.

b) Ta có$\sqrt{4}=2$ và $\sqrt{100}=10$.

Nên $0,2.\sqrt{4}-0,1.\sqrt{100}=0,2.2-0,1.10=0,4-1=-0,6$.

Xem thêm lời giải bài tập Toán lớp 7 Cánh diều hay, chi tiết khác:

Bài 2: Tập hợp R các số thực

Bài 3: Giá trị tuyệt đối của một số thực

Bài 4: Làm tròn số và ước lượng

Bài 5: Tỉ lệ thức

Bài 6: Dãy tỉ số bằng nhau