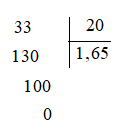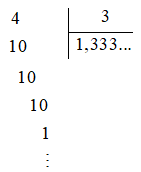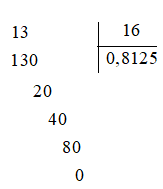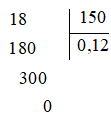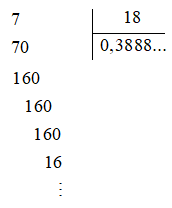Nội dung bài viết

    Xem thêm

    Toán 7 Bài 5 (Cánh diều): Biểu diễn thập phân của số hữu tỉ

    Với giải bài tập Toán lớp 7 Bài 5: Biểu diễn thập phân của số hữu tỉ sách Cánh diều hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 7 Bài 5.

    1 7,826 24/09/2024
    Tải về
    Trang trước
    Chia sẻ
    Trang sau  

    Giải bài tập Toán 7 Bài 5: Biểu diễn thập phân của số hữu tỉ

    Bài giảng Toán 7 Bài 5: Biểu diễn thập phân của số hữu tỉ

    Hoạt động khởi động

    Giải Toán 7 trang 27 Tập 1

    Khởi động trang 27 Toán lớp 7 Tập 1: Viết các số hữu tỉ 110 và 19 dưới dạng số thập phân ta được: 110=0,1 và 19=0,111....

    Hai số thập phân 0,1 và 0,111… khác nhau như thế nào?

    Biểu diễn thập phân của số hữu tỉ như thế nào?

    Lời giải:

    Để trả lời được hai câu hỏi trên, chúng ta cùng tìm hiểu hai mục trong bài ở trang 27 và trang 28.

    Sau bài học này chúng ta sẽ giải quyết được câu hỏi trên như sau:

    • Số thập phân 0,1 là số thập phân hữu hạn.

    Số thập phân 0,111… là số thập phân vô hạn tuần hoàn có chu kì là 1.

    Số 0,111… được viết gọn là 0,(1).

    • Mỗi số hữu tỉ ab với a, b ∈ ℤ; b ≠ 0 đều được biểu diễn bởi một số thập phân của hữu hạn hoặc vô hạn tuần hoàn bằng cách thực hiện phép chia a : b.

    1. Số thập phân hữu hạn và số thập phân vô hạn tuần hoàn

    Hoạt động 1 trang 27 Toán lớp 7 Tập 1: Đặt tính để tính thương: 33 : 20.

    Lời giải:

    Đặt tính 33 : 20 như sau:

    Đặt tính để tính thương: 33 : 20

    Vậy 33 : 20 = 1,65.

    Hoạt động 2 trang 27 Toán lớp 7 Tập 1: Đặt tính để tính thương: 4 : 3.

    Lời giải:

    Đặt tính 4 : 3 như sau:

    Đặt tính để tính thương: 4 : 3

    Vậy 4 : 3 = 1,333…

    Giải Toán 7 trang 28 Tập 1

    Luyện tập 1 trang 28 Toán lớp 7 Tập 1: Sử dụng máy tính cầm tay để viết thương của mỗi phép chia sau dưới dạng số thập phân vô hạn tuần hoàn:

    a) 19;

    b) −  1145.

    Lời giải:

    Sử dụng máy tính cầm tay, ta tính được thương của mỗi phép chia như sau:

    a) 19=  0,11111...;

    b) −  1145=−  0,244444....

    Bài tập

    Giải Toán 7 trang 29 Tập 1

    Bài 1 trang 29 Toán lớp 7 Tập 1: Viết mỗi phân số sau dưới dạng số thập phân hữu hạn: 1316;  −  18150.

    Lời giải:

    Ta có: 1316=13:16.

    Đặt tính 13 : 16 như sau:

    Viết mỗi phân số sau dưới dạng số thập phân hữu hạn: 13/16; -18/150

    Do đó, 13 : 16 = 0,8125.

    Ta có: − 18150=  (−  18)  :  150=−  (18  :  150).

    Đặt tính 18 : 150 như sau:

    Viết mỗi phân số sau dưới dạng số thập phân hữu hạn: 13/16; -18/150

    Khi đó, 18 : 150 = 0,12.

    Do đó, (− 18) : 150 = − (18 : 150) = − 0,12.

    Vậy các phân số 1316;  − 18150 viết dưới dạng số thập phân hữu hạn lần lượt là 0,8125 và −0,12.

    Bài 2 trang 29 Toán lớp 7 Tập 1: Viết mỗi phân số sau dưới dạng số thập phân vô hạn tuần hoàn (dùng dấu ngoặc để nhận rõ chu kì): 5111;  −  718.

    Lời giải:

    Ta có: 5111=5:111.

    Đặt tính 5 : 111 như sau:

    Toán 7 Bài 5: Biểu diễn thập phân của số hữu tỉ- Cánh diều (ảnh 1)

    Do đó, 5 : 111 = 0,045045045… = 0,(045).

    Ta có: − 718=  (−  7)  :  18=−  (7  :  18).

    Đặt tính 7 : 18 như sau:

    Viết mỗi phân số sau dưới dạng số thập phân vô hạn tuần hoàn (dùng dấu ngoặc để nhận rõ chu kì): 5/11; -7/18

    Khi đó, 7 : 18 = 0,3888… = 0,3(8).

    Do đó, (− 7) : 18 = − (18 : 150) = − 0,3888… = − 0,3(8).

    Vậy các phân số 5111;  −  718 viết dưới dạng số thập phân vô hạn tuần hoàn lần lượt là 0,(045) và − 0,3(8).

    Bài 3 trang 29 Toán lớp 7 Tập 1: Viết mỗi số thập phân hữu hạn sau đây dưới dạng phân số tối giản:

    a) 6,5; b) − 1,28; c) – 0,124.

    Lời giải:

    a) Ta có 6,5=6510=65:510:5=132.

    Vậy số thập phân 6,5 viết được dưới dạng phân số tối giản là 132.

    b) − 1,28=− 128100=(− 128):4100:4=− 3225.

    Vậy số thập phân − 1,28 viết được dưới dạng phân số tối giản là − 3225.

    c) − 0,124=− 1241000=− 124:41000:4=− 31250.

    Vậy số thập phân – 0,124 viết được dưới dạng phân số tối giản là − 31250.

    Bài 4 trang 29 Toán lớp 7 Tập 1: Sử dụng máy tính cầm tay để thực hiện mỗi phép chia sau:

    a) 1 : 999; b) 8,5 : 3; c) 14,2 : 3,3.

    Lời giải:

    Sử dụng máy tính cầm tay, ta tính được thương của mỗi phép chia như sau:

    a) 1 : 999 = 0,(001);

    b) 8,5 : 3 = 2,8(3);

    c) 14,2 : 3,3 = 4,(30).

    Lý thuyết Toán 7 Bài 5: Biểu diễn thập phân của một số hữu tỉ - Cánh diều

    1. Số thập phân hữu hạn và số thập phân vô hạn tuần hoàn

    - Các số thập phân chỉ gồm hữu hạn chữ số sau dấu “,” được gọi là số thập phân hữu hạn.

    - Các số thập phân mà trong phần thập phân, bắt đầu từ một hàng nào đó, có một chữ số hay một cụm chữ số liền nhau xuất hiện liên tiếp mãi mãi được gọi là số thập phân vô hạn tuần hoàn. Chữ số hoặc cụm chữ số lặp đi lặp lại mãi mãi đó được gọi là chu kì của số thập phân vô hạn tuần hoàn.

    Ví dụ:

    a) Số thập phân 1,35 chỉ có hai chữ số sau dấu “,” nên nó là số thập phân hữu hạn.

    b) Số thập phân 0,333… có chữ số 3 xuất hiện liên tiếp mãi mãi bắt đầu từ hàng phần mười nên 0,333… là số thập phân vô hạn tuần hoàn với chu kì là 3 và được viết gọn là 0,(3).

    c) Số thập phân 0,12313131…có cụm chữ số liền nhau 31 xuất hiện liên tiếp mãi mãi bắt đầu từ hàng phần nghìn nên số 0,12313131…là số thập phân vô hạn tuần hoàn, chu kì là 31 và được viết gọn là 0,12(31).

    2. Biểu diễn thập phân của số hữu tỉ

    - Mỗi số hữu tỉ đều viết được dưới dạng phân số ab (a,b∈ℤ; b > 0). Thực hiện phép tính

    a : b ta có thể biểu diễn số hữu tỉ đó dưới dạng số thập phân hữu hạn hoặc vô hạn tuần hoàn.

    - Mỗi số hữu tỉ được biểu diễn bởi một số thập phân hữu hạn hoặc vô hạn tuần hoàn.

    Ví dụ:

    a) −716=−0,4375. Vậy số hữu tỉ −716 biểu diễn bởi số thập phân hữu hạn –0,4375.

    b) 43=1,333.... Vậy số hữu tỉ 43 biểu diễn bởi số thập phân vô hạn tuần hoàn 1,(3).

    Xem thêm lời giải bài tập Toán lớp 7 Cánh diều hay, chi tiết khác:

    Bài tập ôn tập chương 1

    Bài 1: Số vô tỉ. Căn bậc hai số học

    Bài 2: Tập hợp R các số thực

    Bài 3: Giá trị tuyệt đối của một số thực

    Bài 4: Làm tròn số và ước lượng

    Tham khảo các loạt bài Toán 7 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 7,826 24/09/2024
    Tải về
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: