Giải Toán 7 Bài 2 (Cánh diều): Phân tích và xử lí dữ liệu

Giải bài tập Toán 7 Bài 2: Phân tích và xử lí dữ liệu

A. Câu hỏi trong bài

Giải Toán 7 trang 9 Tập 2

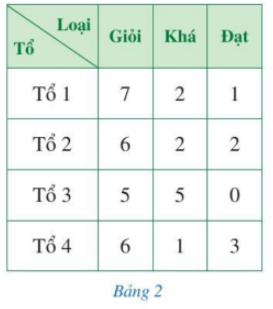
Câu hỏi khởi động trang 9 Toán 7 Tập 2: Xếp loại thi đua bốn tổ lao động của một đội sản xuất được thống kê ở Bảng 2 (đơn vị: người). Bằng cách phân tích và xử lí dữ liệu, hãy cho biết:

a) Đội sản xuất trên có bao nhiêu người?

b) Đội trưởng thông báo rằng tỉ số phần trăm của số lao động giỏi và số người ở cả đội là 65%. Thông báo đó của đội trưởng có đúng không?

Lời giải

Sau bài học này chúng ta sẽ giải quyết được bài toán trên như sau:

a) Số người lao động của tổ 1 là: 7 + 2 + 1 = 10 (người).

Số người lao động của tổ 2 là: 6 + 2 + 2 = 10 (người).

Số người lao động của tổ 3 là: 5 + 5 + 0 = 10 (người).

Số người lao động của tổ 4 là: 6 + 1 + 3 = 10 (người).

Cả bốn tổ có số người là: 10 + 10 + 10 + 10 = 40 (người0.

Vậy đội sản xuất này có 40 người.

b) Số lao động giỏi của đội sản xuất này là: 7 + 6 + 5 + 6 = 24 (người)

Tỉ số phần trăm của số lao động giỏi và số người ở cả đội là: $\frac{24.100}{40}\%=60\%$

Đội trưởng thông báo rằng tỉ số phần trăm của số lao động giỏi và số người ở cả đội là 65% > 60%.

Vậy thông báo của đội trưởng là không đúng.

Hoạt động 1 trang 9 Toán 7 Tập 2: Đọc kĩ các nội dung sau:

Sau khi thu thập, tổ chức, phân loại, biểu diễn dữ liệu bằng bảng hoặc biểu đồ, ta cần phân tích và xử lí các dữ liệu đó để tìm ra những thông tin hữu ích và rút ra kết luận. Thông thường, quá trình phân tích và xử lí dữ liệu dựa trên tính toán và suy luận toán học.

Giải Toán 7 trang 11 Tập 2

Hoạt động 2 trang 11 Toán 7 Tập 2: Đọc kĩ các nội dung sau:

Quá trình phân tích và xử lí dữ liệu giúp chúng ta có thể nhận biết được: tính hợp lí của dữ liệu thống kê, tính hợp lí của kết luận thống kê và cũng có thể bác bỏ kết luận đã nêu ra. Thông thường, để làm được điều đó ta dựa trên những tiêu chí đơn giản hoặc dựa trên tính toán và suy luận toán học.

Giải Toán 7 trang 12 Tập 2

Luyện tập trang 12 Toán 7 Tập 2: Giải bài toán nêu trong phần mở đầu.

Lời giải

a) Số người lao động của tổ 1 là: 7 + 2 + 1 = 10 (người).

Số người lao động của tổ 2 là: 6 + 2 + 2 = 10 (người).

Số người lao động của tổ 3 là: 5 + 5 + 0 = 10 (người).

Số người lao động của tổ 4 là: 6 + 1 + 3 = 10 (người).

Cả bốn tổ có số người là: 10 + 10 + 10 + 10 = 40 (người0.

Vậy đội sản xuất này có 40 người.

b) Số lao động giỏi của đội sản xuất này là: 7 + 6 + 5 + 6 = 24 (người)

Tỉ số phần trăm của số lao động giỏi và số người ở cả đội là: $\frac{24.100}{40}\%=60\%$

Đội trưởng thông báo rằng tỉ số phần trăm của số lao động giỏi và số người ở cả đội là 65% > 60%.

Vậy thông báo của đội trưởng là không đúng.

B. Bài tập

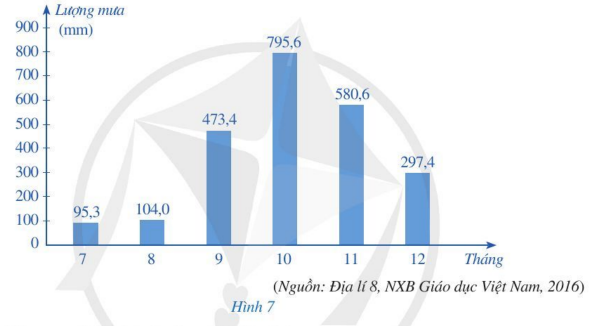
Bài 1 trang 12 Toán 7 Tập 2: Biểu đồ ở Hình 7 biểu diễn lượng mưa tại trạm khí tượng Huế trong sáu tháng cuối năm dương lịch.

a) Nêu đối tượng thống kê và tiêu chí thống kê.

b) Lập bảng số liệu thống kê lượng mưa tại trạm khí tượng Huế theo mẫu sau:

c) Trong các tháng trên, tháng nào có lượng mưa nhiều nhất? Tháng nào có lượng mưa ít nhất?

Lời giải

a) Đối tượng thống kê là sáu tháng cuối năm dương lịch: tháng 7, tháng 8, tháng 9, tháng 10, tháng 11, tháng 12.

Tiêu chí thống kê là lượng mưa (mm) tại trạm khí tượng Huế trong mỗi tháng.

b) Quan sát biểu đồ ở Hình 7 ta thấy”

- Lượng mưa tại trạm khí tượng Huế trong tháng 7 là 95,3 mm.

- Lượng mưa tại trạm khí tượng Huế trong tháng 8 là 1047,0 mm.

- Lượng mưa tại trạm khí tượng Huế trong tháng 9 là 473,4 mm.

- Lượng mưa tại trạm khí tượng Huế trong tháng 10 là 795,6 mm.

- Lượng mưa tại trạm khí tượng Huế trong tháng 11 là 580,6 mm.

- Lượng mưa tại trạm khí tượng Huế trong tháng 12 là 297,4 mm.

Ta có bảng sau:

c) Ta có: 95,3 < 104,0 < 297,4 < 473,4 < 580,6 <795,6.

Vậy trong các tháng trên, tháng có lượng mưa nhiều nhất là tháng 10 (795,6 mm), tháng có lượng mưa ít nhất là tháng 7 (95,3 mm).

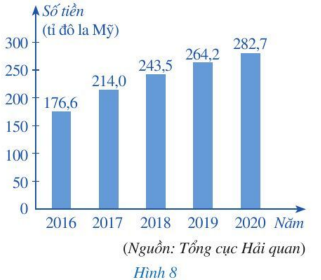
Bài 2 trang 12, 13 Toán 7 Tập 2: Nền kinh tế Việt Nam ngày càng hội nhập sâu rộng với nền kinh tế thế giới. Biểu đồ cột ở Hình 8 biểu diễn kim ngạch xuất khẩu hàng hoá của Việt Nam trong các năm 2016, 2017, 2018, 2019, 2020.

a) Kim ngạch xuất khẩu hàng hoá năm 2019 tăng bao nhiêu phần trăm so với năm 2018 (làm tròn kết quả đến hàng phần mười)?

b) Kim ngạch xuất khẩu hàng hoá năm 2020 tăng bao nhiêu phần trăm so với năm 2019 (làm tròn kết quả đến hàng phần mười)?

Lời giải

Quan sát biểu đồ Hình 8, ta thấy:

- Kim ngạch xuất khẩu hàng hoá của Việt Nam năm 2018 là: 243,5 (tỉ đô la Mỹ).

- Kim ngạch xuất khẩu hàng hoá của Việt Nam năm 2019 là: 264,2 (tỉ đô la Mỹ).

- Kim ngạch xuất khẩu hàng hoá của Việt Nam năm 2020 là: 282,7 (tỉ đô la Mỹ).

a) Tỉ số phần trăm của kim ngạch xuất khẩu hàng hoá năm 2019 so với năm 2018 là khoảng: $\frac{\mathrm{264,2.100}}{\mathrm{243,5}}\%\approx \mathrm{108,5}\%$

Do đó kim ngạch xuất khẩu hàng hoá năm 2019 tăng khoảng 108,5% – 100% = 8,5% so với năm 2018.

Vậy kim ngạch xuất khẩu hàng hoá năm 2019 tăng khoảng 8,5% so với năm 2018.

b) Tỉ số phần trăm của kim ngạch xuất khẩu hàng hoá năm 2020 so với năm 2019 là khoảng: $\frac{\mathrm{282,7.100}}{\mathrm{264,2}}\%\approx \mathrm{107,0}\%$

Do đó kim ngạch xuất khẩu hàng hoá năm 2020 tăng khoảng 107,0% – 100% = 7,0% so với năm 2019.

Vậy kim ngạch xuất khẩu hàng hoá năm 2020 tăng khoảng 7,0% so với năm 2019.

Giải Toán 7 trang 13 Tập 2

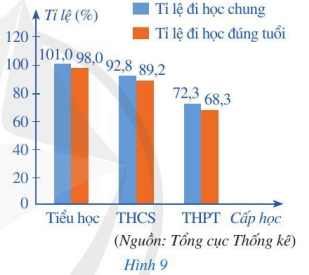
Bài 3 trang 13 Toán 7 Tập 2: Giáo dục phổ thông ở nước ta gồm ba cấp học là: cấp tiểu học, cấp trung học cơ sở (THCS), cấp trung học phổ thông (THPT). Từ năm 2010 đến năm 2019, giáo dục phổ thông đã có sự cải thiện rõ rệt về việc tăng tỉ lệ đi học chung và đi học đúng tuổi. Biểu đồ cột kép ở Hình 9 biểu diễn tỉ lệ đi học chung và tỉ lệ đi học đúng tuổi của mỗi cấp học ở nước ta năm 2019.

a) Tỉ lệ đi học chung của mỗi cấp học ở nước ta năm 2019 là bao nhiêu?

b) Tỉ lệ đi học đúng tuối của mỗi cấp học ở nước ta năm 2019 là bao nhiêu?

c) Tỉ lệ đi học chung của cấp tiểu học là 101,0% được hiểu như thế nào? Giải thích lí do.

Lời giải

a) Quan sát biểu đồ Hình 9, ta thấy:

- Tỉ lệ đi học chung của cấp tiểu học là: 101,0%;

- Tỉ lệ đi học chung của cấp THCS là: 92,8%;

- Tỉ lệ đi học chung của cấp THPT là: 72,3%.

b) Quan sát biểu đồ Hình 9, ta thấy:

- Tỉ lệ đi học đúng tuổi của cấp tiểu học là: 98,0%;

- Tỉ lệ đi học đúng tuổi của cấp THCS là: 89,2%;

- Tỉ lệ đi học đúng tuổi của cấp THPT là: 68,3%.

c) Tỉ lệ đi học chung của một cấp học X được tính bằng tỉ số phần trăm của số học sinh đang đi học cấp học X so với tổng số trẻ em trong độ tuổi cấp học X.

Tỉ lệ đi học chung của cấp tiểu học là 101,0% tức là số trẻ em đi học cấp tiểu học nhiều hơn so với số trẻ em trong độ tuổi cấp tiểu học.

Lí do để giải thích điều này có thể là: một số bạn học sinh đi học sớm/ đi học muộn hơn so với độ tuổi quy định của cấp tiểu học.

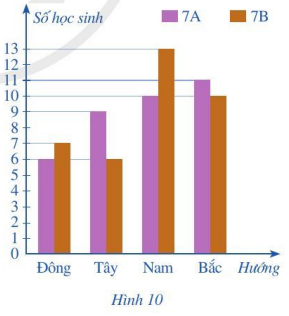
Bài 4 trang 13 Toán 7 Tập 2: Biểu đồ cột kép ở Hình 10 biểu diễn số lượng học sinh lớp 7A và 7B có nhà ở nằm ở bốn hướng Đông, Tây, Nam, Bắc của trường học.

a) Lập bảng số liệu thống kê số lượng học sinh lớp 7A và 7B có nhà nằm ở bốn hướng Đông, Tây, Nam, Bắc của trường học theo mẫu sau:

b) Có 15 bạn trong hai lớp 7A và 7B thường nói rằng: Trong những ngày nắng, mỗi lần đi thẳng từ nhà đến trường vào buổi sáng hay bị chói mắt vì Mặt Trời chiếu thẳng vào mắt. Em có biết vì sao các bạn nói như vậy hay không?

Lời giải

a) Quan sát biểu đồ Hình 10, ta thấy:

- Có 6 bạn học sinh lớp 7A và 7 bạn học sinh lớp 7B có nhà nằm ở hướng Đông;

- Có 9 bạn học sinh lớp 7A và 6 bạn học sinh lớp 7B có nhà nằm ở hướng Tây;

- Có 10 bạn học sinh lớp 7A và 13 bạn học sinh lớp 7B có nhà nằm ở hướng Nam;

- Có 11 bạn học sinh lớp 7A và 10 bạn học sinh lớp 7B có nhà nằm ở hướng Bắc.

Ta có bảng sau:

b) Do Mặt Trời mọc ở hướng Đông nên những bạn có nhà nằm ở hướng Tây mỗi lần đi thẳng đi nhà đến trường vào buổi sáng trong những ngày nắng sẽ bị Mặt Trời chiếu thẳng vào mắt nên sẽ hay bị chói mắt.

Có 9 bạn học sinh lớp 7A và 6 bạn học sinh lớp 7B có nhà nằm ở hướng Tây nên có 15 bạn trong hai lớp sẽ hay bị chói mắt khi đi thẳng từ nhà đến trường.

Lý thuyết Toán 7 Bài 2. Phân tích và xử lí dữ liệu - Cánh diều

1. Phân tích và xử lí dữ liệu để rút ra kết luận

Sau khi thu thập, tổ chức, phân loại, biểu diễn dữ liệu bằng bảng hoặc biểu đồ, ta cần phân tích và xử lí các dữ liệu đó để tìm ra những thông tin hữu ích và rút ra kết luận. Thông thường, quá trình phân tích và xử lí dữ liệu dựa trên tính toán và suy luận toán học.

Ví dụ: Một công ty gồm có bốn đội công nhân may áo khoác jeans. Năng suất may được số lượng áo khoác jeans của bốn đội công nhân đó trong 2 tháng đầu năm được biểu diễn như trong biểu đồ sau:

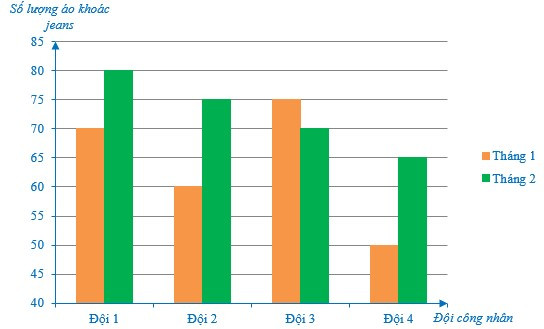
a) Sắp xếp các đội công nhân theo số lượng áo khoác jeans may được ở tháng 1 theo thứ tự từ nhỏ đến lớn.

b) Sắp xếp các đội công nhân theo số lượng áo khoác jeans may được ở tháng 2 theo thứ tự từ nhỏ đến lớn.

c) Đội công nhân nào may được nhiều nhất ở mỗi tháng?

d) Đội công nhân nào may được ít nhất ở mỗi tháng?

e) Trong cả hai tháng, đội công nhân nào có tổng số áo sơ mi may được nhiều nhất?

f) Trong cả hai tháng, đội công nhân nào có tổng số áo sơ mi may được ít nhất?

Hướng dẫn giải

a) Ta có 50 < 60 < 70 < 75 (áo khoác jeans).

Vậy khi sắp xếp các đội công nhân theo số lượng áo khoác jeans may được ở tháng 1 theo thứ tự từ nhỏ đến lớn, ta được: Đội 4; Đội 2; Đội 1; Đội 3.

b) Ta có 65 < 70 < 75 < 80 (áo khoác jeans).

Vậy khi sắp xếp các đội công nhân theo số lượng áo khoác jeans may được ở tháng 2 theo thứ tự từ nhỏ đến lớn, ta được: Đội 4; Đội 3; Đội 2; Đội 1.

c) Ở tháng 1, ta có 50 < 60 < 70 < 75 (áo khoác jeans).

Do đó ở tháng 1, Đội 3 may được nhiều áo khoác jeans nhất.

Ở tháng 2, ta có 65 < 70 < 75 < 80 (áo khoác jeans).

Do đó ở tháng 2, Đội 1 may được nhiều áo khoác jeans nhất.

Vậy đội công nhân may được nhiều áo khoác jeans nhất ở tháng 1, tháng 2 lần lượt là Đội 3 và Đội 1.

d) Ở tháng 1, ta có 50 < 60 < 70 < 75 (áo khoác jeans).

Do đó ở tháng 1, Đội 4 may được ít áo khoác jeans nhất.

Ở tháng 2, ta có 65 < 70 < 75 < 80 (áo khoác jeans).

Do đó ở tháng 2, Đội 4 may được ít áo khoác jeans nhất.

Vậy đội công nhân may được ít áo khoác jeans nhất ở tháng 1, tháng 2 đều là Đội 4.

e) Tổng số áo khoác jeans Đội 1 may được ở cả hai tháng là:

70 + 80 = 150 (áo khoác jeans).

Tổng số áo khoác jeans Đội 2 may được ở cả hai tháng là:

60 + 75 = 135 (áo khoác jeans).

Tổng số áo khoác jeans Đội 3 may được ở cả hai tháng là:

75 + 70 = 145 (áo khoác jeans).

Tổng số áo khoác jeans Đội 4 may được ở cả hai tháng là:

50 + 65 = 115 (áo khoác jeans).

Ta có 115 < 135 < 145 < 150 (áo khoác jeans).

Vậy trong cả hai tháng, Đội 1 có tổng số áo sơ mi may được nhiều nhất.

f) Ta có 115 < 135 < 145 < 150 (áo khoác jeans).

Vậy trong cả hai tháng, Đội 4 có tổng số áo sơ mi may được ít nhất.

2. Tính hợp lí của kết luận thống kê

Quá trình phân tích và xử lí dữ liệu giúp chúng ta có thể nhận biết được: tính hợp lí của dữ liệu thống kê, tính hợp lí của kết luận thống kê và ta cũng có thể bác bỏ kết luận đã nêu ra. Thông thường, để làm được điều đó ta dựa trên những tiêu chí đơn giản hoặc dựa trên tính toán và suy luận toán học.

Ví dụ: Một huấn luyện viên dạy bơi sải ghi lại thời gian (tính theo buổi, mỗi buổi 90 phút) thành thạo môn bơi sải của các học viên như bảng bên:

a) Huấn luyện viên đã khảo sát tổng cộng bao nhiêu học viên?

b) Biết rằng học viên có năng khiếu về môn bơi lội sẽ thành thạo bơi sải trong vòng 8 buổi học. Huấn luyện viên đã đưa ra kết luận rằng: Sau khi khảo sát, số học viên có năng khiếu về môn bơi lội chiếm tỉ lệ 15% so với tổng số học viên tham gia khảo sát. Hỏi kết luận đó của huấn luyện viên có đúng không?

Hướng dẫn giải

a) Số học viên mà huấn luyện viên đã khảo sát là:

1 + 2 + 3 + 10 + 13 + 7 + 4 = 40 (học viên).

Vậy huấn luyện viên đã khảo sát tổng cộng là 40 học viên.

b) Số học viên được huấn luyện viên đánh giá là có năng khiếu về môn bơi lội là:

1 + 2 + 3 = 6 (học viên).

So với tổng số học viên tham gia khảo sát, tỉ lệ học viên được đánh giá là có năng khiếu về môn bơi lội là:

$\frac{6.100}{40}\%=15\%$.

Vậy huấn luyện viên đã kết luận đúng.

Xem thêm lời giải bài tập Toán lớp 7 Cánh diều, chi tiết khác:

Bài 3: Biểu đồ đoạn thẳng

Bài 4: Biểu đồ hình quạt tròn

Bài 5: Biến cố trong một số trò chơi đơn giản

Bài 6: Xác suất của biến cố ngẫu nhiên trong một số trò chơi đơn giản

Bài tập cuối chương 5