Toán 7 Bài 7 (Cánh diều): Đại lượng tỉ lệ thuận

Giải bài tập Toán 7 Bài 7: Đại lượng tỉ lệ thuận

Hoạt động khởi động

Giải Toán 7 trang 59 Tập 1

Khởi động trang 59 Toán lớp 7 Tập 1: Một chiếc máy bay bay với vận tốc không đổi là 900km/h.

Quãng đường s (km) mà máy bay đó bay được và thời gian di chuyển t (h) là hai đại lượng liên hệ với nhau như nào?

Lời giải:

Ta sẽ thấy với vận tốc không đổi, nếu máy bay bay quãng đường ngắn thì thời gian sẽ ít còn nếu bay quãng đường dài thì thời gian sẽ nhiều.

Do đó nếu quãng đường bay tăng thì thời gian bay tăng; quãng đường bay giảm thì thời gian bay giảm.

1. Khái niệm

Hoạt động 1 trang 59 Toán lớp 7 Tập 1: Chiều dài x (m) và khối lượng m (kg) của thanh sắt phi 18 được liên hệ theo công thức m = 2x. Tìm số thích hợp cho vào $\boxed{?}$ trong bảng sau:

Lời giải:

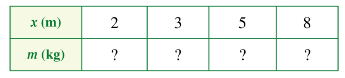
Công thức: m = 2.x.

+) Với x = 2 thì m = 2.2 = 4

+) Với x = 3 thì m = 2.3 = 6

+) Với x = 5 thì m = 2.5 = 10

+) Với x = 8 thì m = 2.8 = 16

Ta có bảng sau:

Luyện tập 1 trang 60 Toán lớp 7 Tập 1: Một chiếc ô tô chuyển động với vận tốc 65km/h.

a) Viết công thức tính quãng đường đi được s (km) theo thời gian t (h) của chuyển động.

b) s và t có phải hai đại lượng tỉ lệ thuận hay không? Nếu có hãy xác định hệ số tỉ lệ của s đối với t.

c) Tính giá trị của s khi t = 0,5; t = $\frac{3}{2}$; t = 2.

Lời giải:

a) Công thức tính quãng đường đi được s (km) theo thời gian t (h) của chuyển động là:

s = vt = 65t (km)

b) s và t là hai đại lượng tỉ lệ thuận. Hệ số tỉ lệ của s đối với t là 65.

c)

+) Với t = 0,5 thì s = 65.0,5 = 32,5 (km)

+) Với t = $\frac{3}{2}$ thì s = 65. $\frac{3}{2}$= 97,5 (km)

+ Với t = 2 thì s = 65.2 = 130 (km).

2. Tính chất

Hoạt động 2 trang 60 Toán lớp 7 Tập 1: Cho biết x; y là hai đại lượng tỉ lệ thuận với nhau:

a) Hãy xác định hệ số tỉ lệ của y đối với x.

b) So sánh các tỉ số: $\frac{y_1}{x_1};\frac{y_2}{x_2};\frac{y_3}{x_3}$.

c) So sánh các tỉ số $\frac{x_1}{x_2}$ và $\frac{y_1}{y_2}$; $\frac{x_1}{x_3}$ và $\frac{y_1}{y_3}$.

Lời giải:

a) Vì x và y là hai đại lượng tỉ lệ thuận với nhau nên y = kx (k ≠ 0)

Với x₁ = 3, y₁ = 9 ta có: 9 = k.3 nên k = 9 : 3 = 3

Vậy hệ số tỉ lệ của y đối với x là 3.

b) Ta có: $\frac{y_1}{x_1}=\frac{9}{3}=3;\frac{y_2}{x_2}=\frac{15}{5}=3;\frac{y_3}{x_3}=\frac{21}{7}=3$

nên $\frac{y_1}{x_1}=\frac{y_2}{x_2}=\frac{y_3}{x_3}=3.$

c) Ta có: $\frac{x_1}{x_2}=\frac{3}{5}$ và $\frac{y_1}{y_2}=\frac{9}{15}=\frac{3}{5}$ nên $\frac{x_1}{x_2}=\frac{y_1}{y_2}$

$\frac{x_1}{x_3}=\frac{3}{7}$ và $\frac{y_1}{y_3}=\frac{9}{21}=\frac{3}{7}$ nên $\frac{x_1}{x_3}=\frac{y_1}{y_3}$ .

3. Một số bài toán

Giải Toán 7 trang 61 Tập 1

Luyện tập 2 trang 61 Toán lớp 7 Tập 1: Một máy in trong 5 phút in được 120 trang. Hỏi trong 3 phút máy in đó in được bao nhiêu trang?

Lời giải:

Gọi x (phút), y (trang) lần lượt là số phút và số trang in được (x; y > 0).

Khi đó, mối quan hệ giữa số phút và số trang in là hai đại lượng tỉ lệ thuận với nhau.

Áp dụng tính chất tỉ lệ thuận ta có: $\frac{y_1}{x_1}=\frac{y_2}{x_2}$ .

Thay x₁ = 5, y₁ = 120, x₂ = 3 ta có: $\frac{120}{5}=\frac{y_2}{3}$ nên $y_2=\frac{120.3}{5}=72$

Vậy trong 3 phút máy in đó in được 72 trang.

Giải Toán 7 trang 62 Tập 1

Luyện tập 3 trang 62 Toán lớp 7 Tập 1: Nhà trường phân công ba lớp 7A; 7B; 7C chăm số 54 cây xanh trong trường. Số cây mỗi lớp cần chăm sóc tỉ lệ thuận với số học sinh của lớp. Biết lớp 7A có 40 học sinh; lớp 7B có 32 học sinh; lớp 7C có 36 học sinh. Tính số cây mỗi lớp cần chăm sóc.

Lời giải:

Gọi x, y, z (cây) lần lượt là số cây mỗi lớp 7A; 7B; 7C chăm sóc được (x; y; z ∈ ℕ*)

Vì số cây mỗi lớp chăm sóc tỉ lệ thuận với số học sinh của lớp nên ta có:

x : y : z = 40 : 32 : 36.

Ta có dãy tỉ số bằng nhau: $\frac{x}{40}=\frac{y}{32}=\frac{z}{36}$.

Áp dụng tính chất dãy tỉ số bằng nhau ta có:

$\frac{x}{40}=\frac{y}{32}=\frac{z}{36}=\frac{x+y+z}{40+32+36}=\frac{54}{108}=\frac{1}{2}$

Ta có:

$\frac{x}{40}=\frac{1}{2}$ suy ra x = 20 (thoả mãn)

$\frac{y}{32}=\frac{1}{2}$ suy ra y = 16 (thoả mãn)

$\frac{z}{36}=\frac{1}{2}$ suy ra z = 18 (thoả mãn)

Vậy số cây ba lớp 7A; 7B; 7C chăm sóc lần lượt là 20 cây; 16 cây; 18 cây.

Bài tập

Bài 1 trang 62 Toán lớp 7 Tập 1: Các giá trị tương ứng của khối lượng m (g) và thể tích V (cm³) được cho bởi bảng sau:

a) Tìm số thích hợp cho $\boxed{?}$.

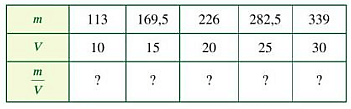
b) Hai đại lượng m và V có tỉ lệ thuận với nhau không? Vì sao?

Lời giải:

a)

+) Với m = 113 và V = 10 nên $\frac{m}{V}=\frac{113}{10}=\mathrm{11,3}$

+) Với m = 169,5 và V = 15 nên $\frac{m}{V}=\frac{\mathrm{169,5}}{15}=\mathrm{11,3}$

+) Với m = 226 và V = 20 nên $\frac{m}{V}=\frac{226}{20}=\mathrm{11,3}$

+) Với m = 282,5 và V = 25 nên $\frac{m}{V}=\frac{\mathrm{282,5}}{25}=\mathrm{11,3}$

+) Với m = 339 và V = 30 nên $\frac{m}{V}=\frac{339}{30}=\mathrm{11,3}$

Ta có bảng sau:

b) Hai đại lượng m và V tỉ lệ thuận với nhau vì từ kết quả câu a ta thấy tỉ số $\frac{m}{V}$ không đổi.

Giải Toán 7 trang 63 Tập 1

Bài 2 trang 63 Toán lớp 7 Tập 1: Cho biết x,y là hai đại lương tỉ lệ thuận với bảng sau:

a) Xác định hệ số tỉ lệ của y đối với x. Viết công thức tính y theo x.

b) Xác định hệ số tỉ lệ của x đối với y. Viết công thức tính x theo y.

c) Tìm số thích hợp cho $\boxed{?}$.

Lời giải:

a) Vì x, y là hai đại lượng tỉ lệ thuận nên y = kx (k ≠ 0)

Với x = 6; y = 4 nên ta có: 4 = 6.k nên k = 4:6 = $\frac{2}{3}$.

Hệ số tỉ lệ của y đối với x là $\frac{2}{3}$.

Công thức tính y theo x là: y = $\frac{2}{3}x$.

b) Theo câu a) y = $\frac{2}{3}$x

Suy ra x = $\frac{3}{2}$y

Vậy: Hệ số tỉ lệ của x đối với y là $\frac{3}{2}$.

Công thức tính x theo y là: x = $\frac{3}{2}$y.

c) Ta sử dụng y = $\frac{2}{3}x$ và x = $\frac{3}{2}y$ ta tính được bảng sau:

Bài 3 trang 63 Toán lớp 7 Tập 1: Trung bình cứ 5 l nước biển chứa 175 g muối. Hỏi trung bình 12 l nước biển chứa bao nhiêu gam muối?

Lời giải:

Gọi x (l), y (g) lần lượt là số lít nước biển và số gam muối có trong số nước biển đó (x; y > 0).

Khi đó, mối quan hệ giữa số lít nước biển và số gam muối có trong số nước biển đó là hai đại lượng tỉ lệ thuận với nhau.

Áp dụng tính chất tỉ lệ thuận ta có: $\frac{y_1}{x_1}=\frac{y_2}{x_2}$.

Thay $x_1=5;y_1=175;x_2=12$ ta có: $\frac{175}{5}=\frac{y_2}{12}$

Do đó $y_2=\frac{12.175}{5}=420$

Vậy sẽ có 420 gam muối trong 12 lít nước biển.

Bài 4 trang 63 Toán lớp 7 Tập 1: Cứ 12 phút, một chiếc máy làm được 27 sản phẩm. Để làm được 45 sản phẩm như thế thì chiếc mấy đó cần bao nhiêu phút

Lời giải:

Gọi x (phút), y (sản phầm) lần lượt là số phút và số sản phẩm mà chiếc máy đó làm được (x; y > 0).

Khi đó, mối quan hệ giữa số phút và số sản phẩm mà chiếc máy đó làm được được là hai đại lượng tỉ lệ thuận với nhau.

Áp dụng tính chất tỉ lệ thuận ta có: $\frac{y_1}{x_1}=\frac{y_2}{x_2}$.

Thay $x_1=12;y_1=27;y_2=45$ ta có: $\frac{27}{12}=\frac{45}{x_2}$ nên $x_2=\frac{12.45}{27}=20$

Vậy để làm được 45 sản phẩm chiếc máy đó cần 20 phút.

Bài 5 trang 63 Toán lớp 7 Tập 1: Để làm thuốc ho người ta ngâm chanh đào với mật ong và đường phèn theo tỉ lệ. Cứ 0,5 kg chanh đào thì cần 250 g đường phèn và 0,5 l mật ong. Với tỉ lệ đó, nếu muốn ngâm 2,5 kg chanh đào thì cần bao nhiêu ki – lô – gam đường phèn và bao nhiêu kg mật ong?

Lời giải:

Đổi 250 g = 0,25 kg.

Đặt x (kg), y (kg), z (lít) lần lượt là số kg chanh đào, số kg đường phèn và số lít mật ong để làm thuốc ho theo tỉ lệ (x; y; z > 0).

Khi đó mối quan hệ giữa số kg chanh đào, số kg đường phèn và số lít mật ong tỉ lệ thuận với nhau.

Giả sử cần x₁ = 0,5 (kg) chanh đào thì cần y₁ = 0,25 (kg) đường phèn và và z₁ = 0,5 (lít) mật ong.

Cần x₂ = 2,5 (kg) chanh đào thì cần y₂ (kg) đường phèn và và z₂ (lít) mật ong.

• Ta có: $\frac{y_1}{x_1}=\frac{y_2}{x_2}$

Thay x₁ = 0,5; y₁ = 0,25; x₂ = 2,5 ta có: $\frac{0,25}{0,5}=\frac{y_2}{2,5}$

Do đó $y_2=\frac{0,25.2,5}{0,5}=1,25$

• Ta có: $\frac{x_1}{x_2}=\frac{z_1}{z_2}$

Thay $x_1=0,5;z_1=0,5;x_2=2,5$ ta có: $\frac{0,5}{0,5}=\frac{2,5}{z_2}$

Do đó $z_2=\frac{0,5.2,5}{0,5}=2,5$

Vậy để ngâm 2,5 kg chanh đào làm thuốc ho theo tỉ lệ thì cần 1,25kg đường phèn và 2,5 lít mật ong.

Bài 6 trang 63 Toán lớp 7 Tập 1: Theo như công bố chính thức từ hãng sản xuất, chiếc xe ô tô của cô Hạnh có mức tiêu thụ nhiên liệu như sau:

• 9,9 l/100 km trên đường hỗn hợp;

• 13,9 l/100 km trên đường đô thị;

• 7,5 l/100 km trên đường cao tốc.

a) Theo thông số trên, nếu trong bình xăng của chiếc xe ô tô đó có 65 lít xăng thì cô Hạnh đi được bao nhiêu ki – lô – mét (làm tròn kết quả đến hàng đơn vị) khi cô đi trên đường đô thị? Đường hỗn hợp? Đường cao tốc?

b) Để đi quãng đường 400 km trên đường đô thị, trong bình xăng chiếc xe ô tô của cô Hạnh cần có tối thiểu bao nhiêu lít xăng?

c) Để đi quãng đường 300 km trên đường hỗn hợp và 300km trên đường cao tốc, trong bình xăng chiếc xe ô tô của cô Hạnh cần tối thiểu bao nhiêu lít xăng?

Lời giải:

a) Với 65 lít xăng, cô Hạnh có thể đi số km đường đô thị là:

65.100:13,9 $\approx 468$ (km)

Với 65 lít xăng, cô Hạnh có thể đi số km đường hỗn hợp là:

65.100:9,9 $\approx 657$ (km)

Với 65 lít xăng, cô Hạnh có thể đi số km đường cao tốc là:

65.100:7,5 $\approx 867$ (km)

b) Để đi quãng đường 400km trên đường đô thị, trong bình xăng của ô tô cô Hạnh phải có tối thiểu số lít xăng là:

400.13,9:100 = 55 (lít)

c) Đi 300km đường hỗn hợp hết số lít xăng là: 300.9,9:100 = 29,7 (lít)

Đi 300km đường cao tốc hết số lít xăng là: 300.7,5:100 = 22,5 (lít)

Để đi quãng đường 300km trên đường hỗn hợp và 300km trên đường cao tốc, trong bình xăng chiếc xe ô tô của cô Hạnh cần tối thiếu số lít xăng là:

29,7 + 22,5 = 52,2 (lít).

Lý thuyết Toán 7 Bài 7. Đại lượng tỉ lệ thuận – Cánh diều

1. Khái niệm

- Nếu đại lượng y liên hệ với đại lượng x theo công thức y = kx (với k là một hằng số khác 0) thì ta nói y tỉ lệ thuận với x theo hệ số tỉ lệ k.

- Nếu y tỉ lệ thuận với x theo hệ số tỉ lệ k thì x tỉ lệ thuận với y theo hệ số tỉ lệ $\frac{1}{\mathrm{k}}$. Ta nói x và y là hai đại lượng tỉ lệ thuận với nhau.

Ví dụ:

a) Nếu y = 2x thì ta nói y tỉ lệ thuận với x theo hệ số tỉ lệ 2. Khi đó x cũng tỉ lệ thuận với y theo hệ số tỉ lệ $\frac{1}{2}$.

b) Chu vi đường tròn C và đường kính d liên hệ với nhau bởi công thức C = π . d. Khi đó C tỉ lệ thuận với d theo hệ số tỉ lệ là π (π ≈ 3,14).

2. Tính chất

Nếu hai đại lượng tỉ lệ thuận với nhau thì:

- Tỉ số hai giá trị tương ứng của chúng luôn không đổi;

- Tỉ số hai giá trị bất kì của đại lượng này bằng tỉ số hai giá trị tương ứng của đại lượng kia.

Cụ thể: Giả sử y tỉ lệ thuận với x theo hệ số tỉ lệ k. Với mỗi giá trị x₁, x₂, x₃,… khác 0 của x, ta có một giá trị tương ứng y₁, y₂, y_3­, … của y. Khi đó:

$\frac{{\mathrm{y}}_1}{{\mathrm{x}}_1}=\frac{{\mathrm{y}}_2}{{\mathrm{x}}_2}=\frac{{\mathrm{y}}_3}{{\mathrm{x}}_3}=\mathrm{...}=\mathrm{k};$

$\frac{{\mathrm{x}}_1}{{\mathrm{x}}_2}=\frac{{\mathrm{y}}_1}{{\mathrm{y}}_2};\frac{{\mathrm{x}}_1}{{\mathrm{x}}_3}=\frac{{\mathrm{y}}_1}{{\mathrm{y}}_3};\mathrm{...}$

Ví dụ: Khối lượng và thể tích của các thanh kim loại đồng chất là hai đại lượng tỉ lệ thuận với nhau. Biết hai thanh kim loại đồng chất có thể tích lần lượt là 10 cm³ và 15 cm³. Tính tỉ số khối lượng của hai thanh kim loại đó.

Hướng dẫn giải

Gọi m₁ (gam) và m₂ (gam) lần lượt là khối lượng của hai thanh kim loại có thể tích 10 cm³ và 15 cm³.

Áp dụng tính chất của đại lượng tỉ lệ thuận ta có $\frac{{\mathrm{m}}_1}{{\mathrm{m}}_2}=\frac{10}{15}=\frac{2}{3}$.

3. Một số bài toán

Bài toán 1: Một máy in trong 5 phút in được 120 trang. Hỏi trong 3 phút máy in đó in được bao nhiêu trang?

Hướng dẫn giải

Gọi x (phút), y (trang) lần lượt là thời gian in và số trang mà máy in đã in được. Khi đó mỗi quan hệ giữa thời gian (x) và số trang in được (y) được cho bởi bảng sau:

Ta có thời gian in tỉ lệ thuận với số trang in được theo hệ số tỉ lệ $\mathrm{k}=\frac{120}{5}=24$.

Suy ra $\frac{{\mathrm{y}}_2}{3}=24$. Vì thế y₂ = 24 . 3 = 72.

Vậy trong 3 phút máy in in được 72 trang.

Bài toán 2: Hai thanh chì có thể tích là 12 cm³ và 17 cm³. Hỏi mỗi thanh nặng bao nhiêu gam, biết rằng thanh thứ hai nặng hơn thanh thứ nhất 56,5 g?

Hướng dẫn giải

Gọi khối lượng của hai thanh chì tương ứng là m₁ gam và m₂ gam. Khi đó m₂ – m₁ = 56,5 (g)

Do khối lượng và thể tích của vật thể là hai đại lượng tỉ lệ thuận với nhau. Do đó, ta có:

$\frac{{\mathrm{m}}_1}{12}=\frac{{\mathrm{m}}_2}{17}$.

Áp dụng tính chất dãy tỉ số bằng nhau, ta có: $\frac{{\mathrm{m}}_1}{12}=\frac{{\mathrm{m}}_2}{17}=\frac{{\mathrm{m}}_2-{\mathrm{m}}_1}{17-12}=\frac{56,5}{5}=11,3$.

Suy ra m₁ = 12 . 11,3 = 135,6 ; m₂ = 17 . 11,3 = 192,1.

Vậy hai thanh chì có khối lượng là 135,6 gam và 192,1 gam.

Xem thêm lời giải bài tập Toán lớp 7 Cánh diều hay, chi tiết khác:

Bài 8: Đại lượng tỉ lệ nghịch

Bài tập ôn tập chương 2

Chủ đề 1: Một số hình thức khuyến mãi trong kinh doanh

Chủ đề 2: Tạo đồ dùng dạng hình lăng trụ đứng

Bài 1: Hình hộp chữ nhật. Hình lập phương