Toán 7 Bài 2 (Cánh diều): Hình lăng trụ đứng tam giác. Hình lăng trụ đứng tứ giác
Với giải bài tập Toán lớp 7 Bài 2: Hình lăng trụ đứng tam giác. Hình lăng trụ đứng tứ giác sách Cánh diều hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 7 Bài 2
Giải bài tập Toán 7 Bài 2: Hình lăng trụ đứng tam giác. Hình lăng trụ đứng tứ giác
Hoạt động khởi động
Những hình khối có dạng như trên được gọi là hình gì?
Lời giải:
Chúng ta thấy các hình khối trên có các mặt là các hình tam giác; hình chữ nhật hoặc hình tứ giác.
Vậy để trả lời cho câu hỏi này chúng ta cùng tìm hiểu về bài học này.
Sau bài học này chúng ta có thể giải quyết câu hỏi trên như sau:
Hình 18 là hình lăng trụ đứng tam giác.
Hình 19 là hình lăng trụ đứng tứ giác.
1. Hình lăng trụ đứng tam giác
Hoạt động 1 trang 81 Toán lớp 7 Tập 1:Thực hiện các hoạt động sau:
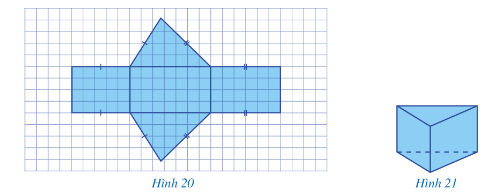
a) Vẽ trên giấy kẻ ô vuông hai hình tam giác và ba hình chữ nhật như Hình 20;
Lời giải:
a) b) Học sinh thực hiện theo hướng dẫn.
c) Quan sát hình lăng trụ đứng tam giác ở Hình 21 ta thấy: Hình lăng trụ đứng tam giác ở Hình 21 có 5 mặt, 9 cạnh và 6 đỉnh.
 Lời giải:
Lời giải:
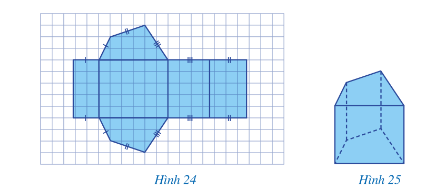
Quan sát lăng trụ đứng tam giác ở Hình 22, ta có:
Các mặt của hình lăng trụ đứng tam giác ở Hình 22 là: ABC; A’B’C’; AA’B’B; AA’C’C; BB’C’C.
Các cạnh của hình lăng trụ đứng tam giác ở Hình 22 là: AB; AC; BC; A’B’; A’C’; B’C’; AA’; BB’; CC’.
Các đỉnh của hình lăng trụ đứng tam giác ở Hình 22 là: A; B; C: A’; B’; C’.
 a) Đáy dưới ABC và đáy trên A'B'C' là hình gì?
a) Đáy dưới ABC và đáy trên A'B'C' là hình gì?
c) So sánh độ dài hai cạnh bên AA' và CC'.
Lời giải:
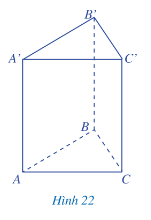
Ở hình 23 ta quan sát được
a) Đáy dưới ABC và đáy trên A’B’C’ là hình tam giác.
b) Mặt bên AA’C’C là hình gì hình chữ nhật.
c) Độ dài cạnh bên AA’ và CC’ là bằng nhau.
2. Hình lăng trụ đứng tứ giác
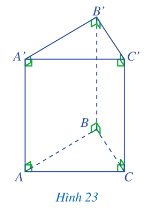
Hoạt động 4 trang 82 Toán lớp 7 Tập 1: Thực hiện các hoạt động sau:
Lời giải:
a) b) Học sinh tự thực hiện theo hướng dẫn.
c) Quan sát hình lăng trụ đứng tứ giác ở Hình 25 ta thấy hình lăng trụ đứng tứ giác có 6 mặt, 12 cạnh và 8 đỉnh.
 Lời giải:
Lời giải:
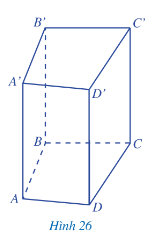
Ta quan sát lăng trụ đứng tứ giác ở Hình 26:
Tên các mặt là: ABCD; A’B’C’D’; AA’B’B; BB’C’C; CC’D’D; DD’AA.
Tên các cạnh là: AB; BC; CD; DA; A’B’; B’C’; C’D’; D’A’; AA’; BB’; CC’; DD’.
Các đỉnh: A; B; C; D; A’; B’; C’; D’.
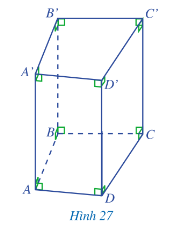 a) Đáy dưới ABCD và đáy trên A'B'C'D' là hình gì?
a) Đáy dưới ABCD và đáy trên A'B'C'D' là hình gì?
c) So sánh độ dài hai cạnh bên AA' và DD'.
Lời giải:
a) Ta quan sát thấy đáy dưới ABCD và đáy trên A’B’C’D’ là hình tứ giác.
b) Ta quan sát thấy mặt bên AA’D’D là hình hình chữ nhật.
c) Ta quan sát thấy độ dài hai cạnh bên AA’ và DD’ là hai cạnh bằng nhau.
3. Thể tích và diện tích xung quanh của hình lăng trụ đứng tam giác, hình lăng trụ đứng tứ giác
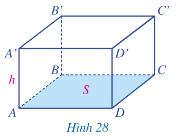 Tính thể tích hình hộp chữ nhật ABCD.A'B'C'D' theo S và h.
Tính thể tích hình hộp chữ nhật ABCD.A'B'C'D' theo S và h.
Lời giải:
Công thức tính thể tích hình hộp chữ nhật ABCD.A'B'C'D' là: V = S.h.
Hoạt động 8 trang 84 Toán lớp 7 Tập 1: Quan sát hình lăng trụ đứng tam giác ABC.A'B'C' (Hình 31).
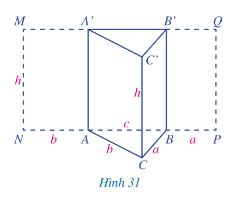 Trải mặt bên AA'C'C thành hình chữ nhật AA'MN. Trải mặt bên BB'C'C thành hình chữ nhật BB'QP.
Trải mặt bên AA'C'C thành hình chữ nhật AA'MN. Trải mặt bên BB'C'C thành hình chữ nhật BB'QP.
a) Tính diện tích hình chữ nhật MNPQ.
Lời giải:
a) Ta thấy diện tích hình chữ nhật MNPO bằng tổng diện tích của ba hình chữ nhật MA’AN; AA’B’B; B’BPQ.
Diện tích hình chữ nhật MA’AN là:
S1 = b.h (đơn vị diện tích)
Diện tích hình chữ nhật AA’B’B là:
S2 = c.h (đơn vị diện tích)
Diện tích hình chữ nhật B’BPQ là:
S3 = a.h (đơn vị diện tích)
Diện tích hình chữ nhật MNPQ là:
S = ah + bh + ch = (a + b + c).h (đơn vị diện tích) (1)
b) Chu vi đáy của hình lăng trụ đứng tam giác là:
BC + AC + AB = a + b + c (đơn vị độ dài)
Tích của chu vi đáy của hình lăng trụ đứng tam giác ABC.A’B”C” và chiều cao của hình lăng trụ đó là: (a + b + c).h (2).
Từ (1) và (2) ta có diện tích hình chữ nhật MNPQ bằng với tích chu vi đáy với chiều cao của hình lăng trụ đứng tam giác ABC.A’B’C’.
c) Diện tích hình chữ nhật MNPQ bằng với diện tích xung quanh của hình lăng trụ đứng tam giác ABC.A’B’C’.
Bài tập
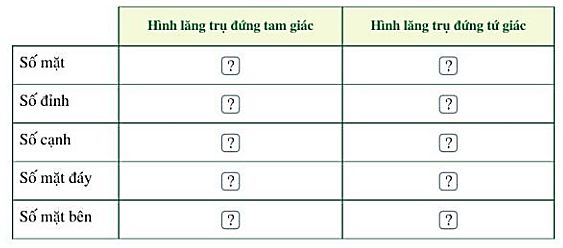
Bài 1 trang 85 Toán lớp 7 Tập 1: Tìm số thích hợp cho ? trong bảng sau:
 Lời giải:
Lời giải:
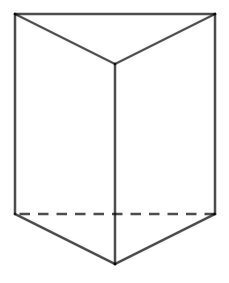
Hình lăng trụ đứng tam giác |
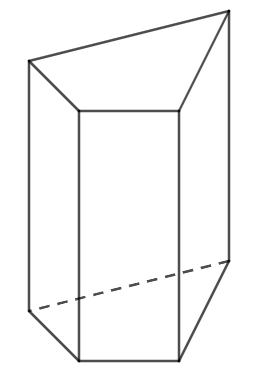
Hình lăng trụ đứng tứ giác |
Hình lăng trụ đứng tam giác có 5 mặt; 6 đỉnh; 9 cạnh; 2 mặt đáy; 3 mặt bên.
Hình lăng trụ đứng tam giác có 6 mặt; 8 đỉnh; 12 cạnh; 2 mặt đáy; 4 mặt bên.
Ta có bảng sau:
|
|
Hình lăng trụ đứng tam giác |
Hình lăng trụ đứng tứ giác |
|
Số mặt |
5 |
6 |
|
Số đỉnh |
6 |
8 |
|
Số cạnh |
9 |
12 |
|
Số mặt đáy |
2 |
2 |
|
Số mặt bên |
3 |
4 |
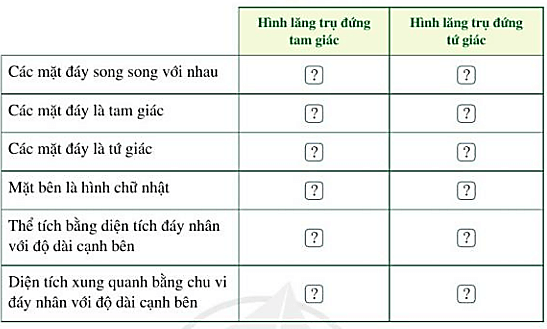
Lời giải:
|
|
Hình lăng trụ đứng tam giác |
Hình lăng trụ đứng tứ giác |
|
Các mặt đáy song song với nhau. |
Đ |
Đ |
|
Các mặt đáy là tam giác. |
Đ |
S |
|
Các mặt đáy là tứ giác. |
S |
Đ |
|
Mặt bên là hình chữ nhật. |
Đ |
Đ |
|
Thể tích bằng diện tích đáy nhân với độ dài cạnh bên. |
Đ |
Đ |
|
Diện tích xung quang bằng chu vi đáy nhân với độ dài cạnh bên. |
Đ |
Đ |
Bài 3 trang 86 Toán lớp 7 Tập 1: Cho các hình lăng trụ đứng ở Hình 33a và Hình 33b:
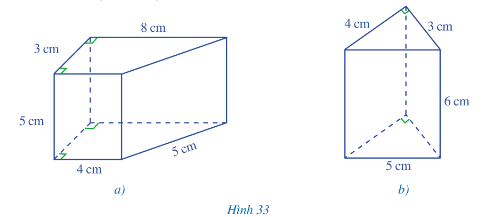 (i) Hình nào trong các hình 33a, 33b là hình lăng trụ đứng tam giác? Hình lăng trụ đứng tứ giác?
(i) Hình nào trong các hình 33a, 33b là hình lăng trụ đứng tam giác? Hình lăng trụ đứng tứ giác?
(ii) Tính diện tích xung quanh của hình lăng trụ đứng tam giác, hình lăng trụ đứng tứ giác ở Hình 33
(iii) Tính thể tích của hình lăng trụ đứng tam giác, hình lăng trụ đứng tứ giác có ở Hình 33
Lời giải:
(i) Trong hai hình 33a, 33b thì hình 33b là hình lăng trụ đứng tam giác, Hình 33a là hình lăng trụ đứng tứ giác.
(ii)
Hình lăng trụ đứng tứ giác (hình 33a)
Chu vi đáy là: 3 + 4 + 5 + 8 = 20 (cm)
Diện tích xung quanh là: 20.5 = 100 (cm2).
Hình lăng trụ đứng tam giác (hình 33b)
Chu vi đáy là: 3 + 4 + 5 = 12 (cm)
Diện tích xung quanh là: 12.6 = 72 (cm2)
(iii)
Hình lăng trụ đứng tam giác (hình 33b)
Diện tích đáy là: S = 123.4=6(cm2)
Thể tích hình lăng trụ đứng tam giác là:
V1 = S.h = 6.6 = 36 (cm3)
Hình lăng trụ đứng tứ giác (hình 33a)
Diện tích đáy là: S = (4+8).52 = 30 (cm2)
Thể tích hình lăng trụ đứng tứ giác là:
V2 = S.h = 30.5 = 150 (cm3).
Lý thuyết Toán 7 Bài 2. Hình lăng trụ đứng tam giác. Hình lăng trụ đứng tứ giác- Cánh diều
1. Hình lăng trụ đứng tam giác
- Hình lăng trụ đứng tam giác có 5 mặt, 9 cạnh, 6 đỉnh.
- Hai mặt đáy cùng là tam giác và nằm trong hai mặt phẳng song song với nhau; Mỗi mặt bên là hình chữ nhật;
- Các cạnh bên bằng nhau;
- Chiều cao của hình lăng trụ đứng tam giác là độ dài cạnh bên.
Ví dụ:
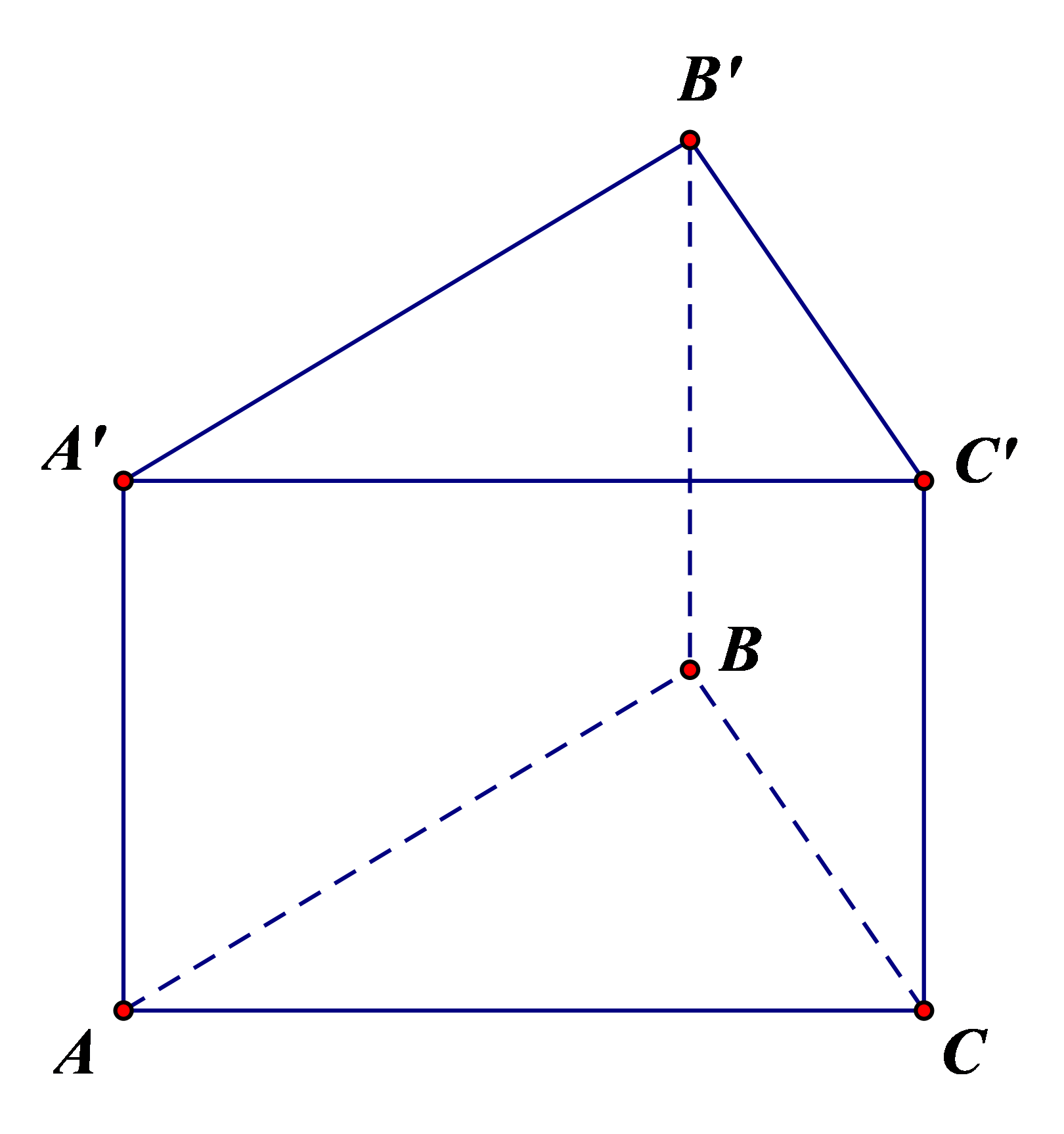
Hình lăng trụ đứng tam giác ABC.A'B'C' có:
- Đáy dưới là tam giác ABC, đáy trên là tam giác A'B'C';
Các mặt bên là các hình chữ nhật: AA'B'B, BB'C'C, CC'A'A;
- Các cạnh:
+ Cạnh đáy: AB, BC, CA, A'B', B'C', C'A'
+ Cạnh bên: AA', BB', CC';
- Các đỉnh: A, B, C, A', B', C'.
- Chiều cao là độ dài một cạnh bên: AA' hoặc BB' hoặc CC'.
2. Hình lăng trụ đứng tứ giác
- Lăng trụ đứng tứ giác có 6 mặt, 12 cạnh, 8 đỉnh.
- Hai mặt đáy cùng là tứ giác và song song với nhau. Mỗi mặt bên là hình chữ nhật.
- Các cạnh bên bằng nhau.
- Chiều cao của hình lăng trụ đứng tứ giác là độ dài một cạnh bên.
Ví dụ:
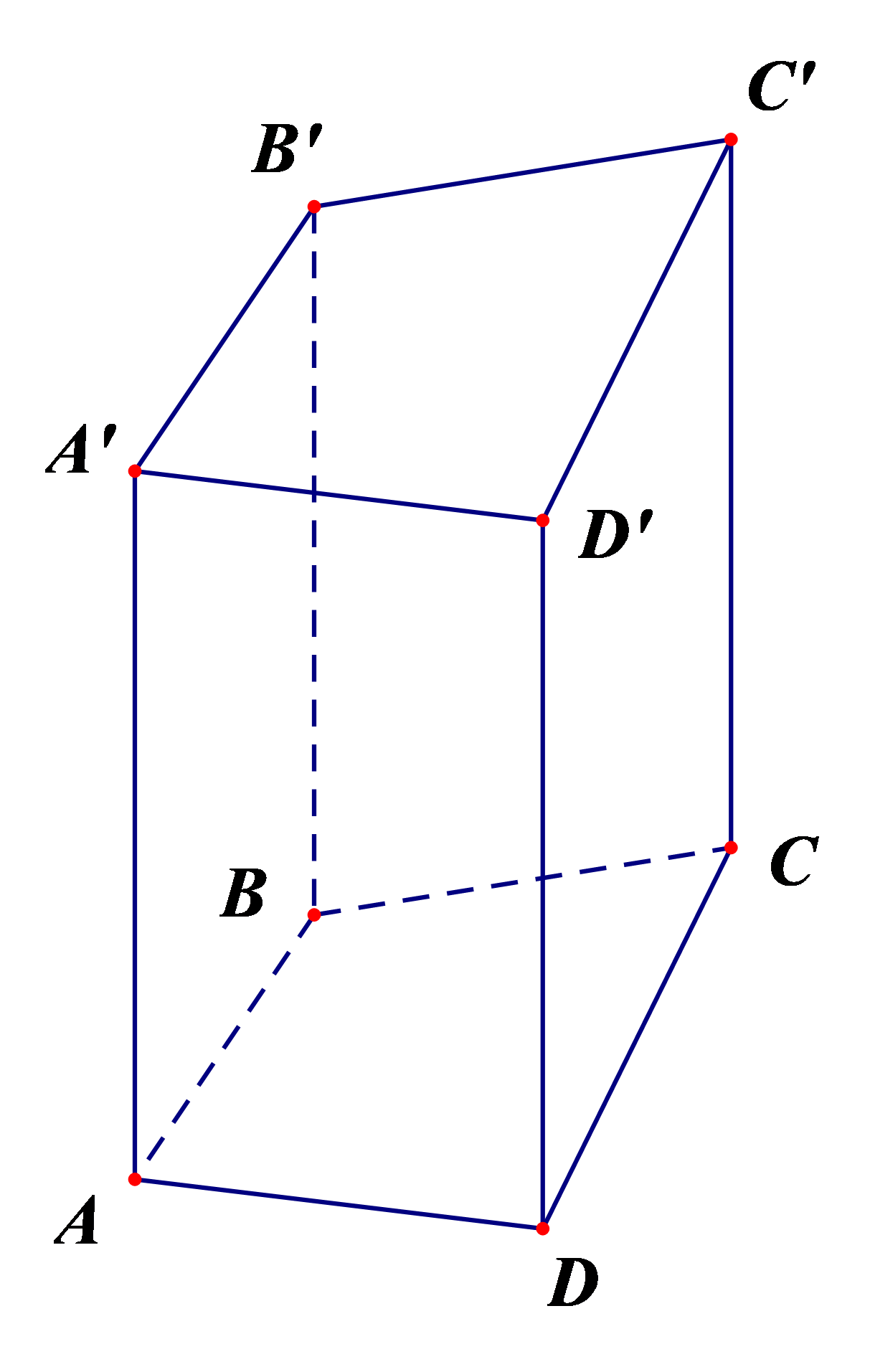
Hình lăng trụ đứng tứ giác ABCD.A'B'C'D' có:
- Đáy dưới là tứ giác ABCD, đáy trên là tứ giác A'B'C'D';
Các mặt bên là các hình chữ nhật: AA'B'B, BB'C'C, CC'D'D, DD'A'A;
- Các cạnh:
+ Cạnh đáy: AB, BC, CD, DA, A'B', B'C', C'D', D'A'
+ Các cạnh bên: AA', BB', CC', DD' bằng nhau.
- Các đỉnh: A, B, C, D, A', B', C', D'.
- Chiều cao là độ dài một cạnh bên: AA' hoặc BB' hoặc CC' hoặc DD'.
Chú ý: Hình hộp chữ nhật và hình lập phương cũng là lăng trụ đứng tứ giác.
3. Thể tích và diện tích xung quanh của hình lăng trụ đứng tam giác, lăng trụ đứng tứ giác
- Thể tích của hình lăng trụ đứng tứ giác bằng diện tích đáy nhân với chiều cao.
Tức là: V = S . h, trong đó V là thể tích, S là diện tích đáy và h là chiều cao của hình lăng trụ đứng tứ giác.
- Thể tích của hình lăng trụ đứng tam giác bằng diện tích đáy nhân với chiều cao.
Tức là: V = S . h, trong đó V là thể tích, S là diện tích đáy và h là chiều cao của hình lăng trụ đứng tam giác.
- Diện tích xung quanh của hình lăng trụ đứng tam giác hay hình lăng trụ đứng tứ giác bằng chu vi đáy nhân với chiều cao.
Tức là Sxq = C . h, trong đó Sxq là diện tích xung quanh, C là chu vi đáy, h là chiều cao của hình lăng trụ đứng tam giác hay của hình lăng trụ đứng tứ giác.
Ví dụ:

a) Cho hình lăng trụ đứng tam giác ABC.A'B'C'.
Sxq = C . h, trong đó C là chu vi của tam giác ABC (hoặc tam giác A'B'C'), h là độ dài cạnh bên AA' (hoặc BB, hoặc CC').
V = S . h, trong đó S là diện tích tam giác ABC (hoặc A'B'C'), h là độ dài cạnh bên AA' (hoặc BB' hoặc CC').
b) Cho hình lăng trụ đứng tứ giác ABCD.A'B'C'D':
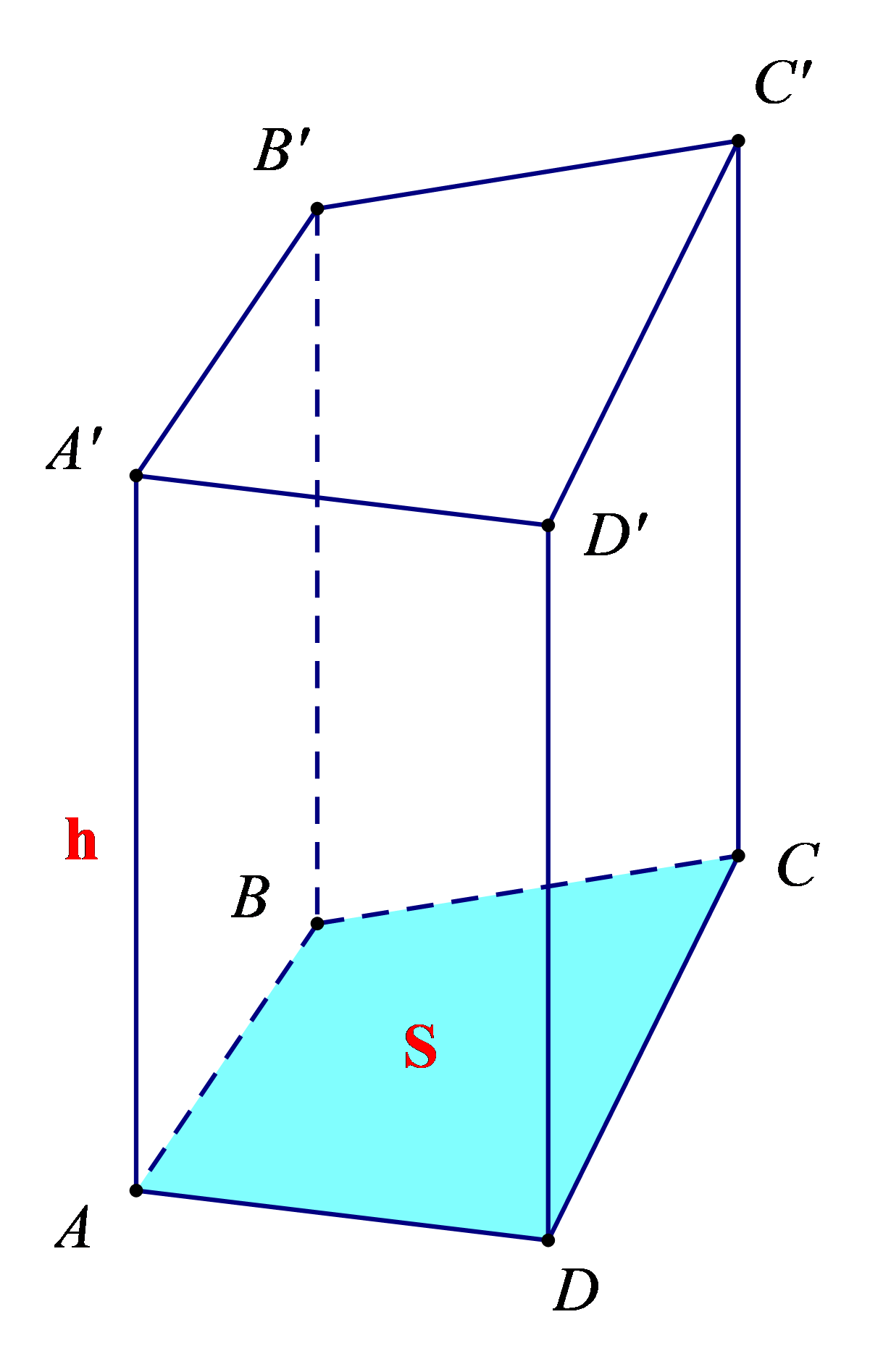
Sxq = C . h, trong đó C là chu vi của tứ giác ABCD (hoặc tứ giác A'B'C'D'), h là độ dài cạnh bên AA' (hoặc BB, hoặc CC', hoặc DD').
V = S . h, trong đó S là diện tích tứ giác ABCD (hoặc A'B'C'D'), h là độ dài cạnh bên AA' (hoặc BB' hoặc CC', hoặc DD').
Xem thêm lời giải bài tập Toán lớp 7 Cánh diều hay, chi tiết khác:
Bài 2: Tia phân giác của một góc
Xem thêm các chương trình khác:
- Soạn văn lớp 7 (hay nhất)– Cánh Diều
- Tác giả tác phẩm Ngữ văn lớp 7 – Cánh Diều
- Tóm tắt tác phẩm Ngữ văn lớp 7 – Cánh Diều
- Bố cục tác phẩm Ngữ văn lớp 7 – Cánh Diều
- Nội dung chính tác phẩm Ngữ văn lớp 7 – Cánh Diều
- Giải sbt Ngữ văn lớp 7 – Cánh Diều
- Văn mẫu lớp 7 – Cánh Diều
- Soạn văn lớp 7 (ngắn nhất) – Cánh Diều
- Giải VBT Ngữ văn lớp 7 – Cánh diều
- Giải sgk Tiếng Anh 7 - Explore English
- Giải sgk Tiếng Anh 7 – ilearn Smart World
- Trọn bộ Từ vựng Tiếng Anh 7 ilearn Smart World đầy đủ nhất
- Ngữ pháp Tiếng Anh 7 i-learn Smart World
- Bài tập Tiếng Anh 7 iLearn Smart World theo Unit có đáp án
- Giải sbt Tiếng Anh 7 - ilearn Smart World
- Giải sgk Lịch sử 7 – Cánh Diều
- Lý thuyết Lịch Sử 7 – Cánh Diều
- Giải sbt Lịch sử 7 – Cánh Diều
- Giải VBT Lịch sử 7 – Cánh diều
- Giải sgk Khoa học tự nhiên 7 – Cánh Diều
- Lý thuyết Khoa học tự nhiên 7 – Cánh Diều
- Giải sbt Khoa học tự nhiên 7 – Cánh Diều
- Giải sgk Địa lí 7 – Cánh Diều
- Lý thuyết Địa Lí 7 – Cánh Diều
- Giải sbt Địa lí 7 – Cánh Diều
- Giải VBT Địa lí 7 – Cánh diều
- Giải sgk Tin học 7 – Cánh Diều
- Lý thuyết Tin học 7 – Cánh Diều
- Giải sbt Tin học 7 – Cánh Diều
- Giải sgk Giáo dục công dân 7 – Cánh Diều
- Lý thuyết Giáo dục công dân 7 – Cánh Diều
- Giải sbt Giáo dục công dân 7 – Cánh Diều
- Giải sgk Hoạt động trải nghiệm 7 – Cánh Diều
- Giải sbt Hoạt động trải nghiệm 7 – Cánh Diều
- Giải sgk Công nghệ 7 – Cánh Diều
- Lý thuyết Công nghệ 7 – Cánh Diều
- Giải sbt Công nghệ 7 – Cánh Diều
- Giải sgk Giáo dục thể chất 7 – Cánh Diều
- Giải sgk Âm nhạc 7 – Cánh Diều