Toán 7 (Cánh diều) Bài tập cuối chương 3

Giải bài tập Toán 7 Bài tập cuối chương 3

Bài tập

Giải Toán 7 trang 87 Tập 1

Bài 1 trang 87 Toán lớp 7 Tập 1: Quan sát Hình 11, Hình 12 và chọn từ “đúng (Đ)”, “sai (S)” thích hợp cho $\boxed{?}$ trong bảng sau:

Lời giải:

Bài 2 trang 87 Toán lớp 7 Tập 1:

a) Cho một hình lăng trụ đứng có độ dài cạnh bên là 10 cm và đáy là tam giác. Biết tam giác đó có độ dài các cạnh lần lượt là 4 cm, 5 cm, 6 cm. Tính diện tích xung quanh của hình lăng trụ đứng đã cho.

b) Cho một hình lăng trụ đứng có độ dài cạnh bên là 20 cm và đáy là một hình thang cân. Biết hình thang cân đó có độ dài cạnh bên là 13 cm, độ dài hai đáy lần lượt là 8 cm, 18 cm và chiều cao là 12 cm. Tính diện tích toàn phần (tức là tổng diện tích các mặt) của hình lăng trụ đứng đã cho.

Lời giải:

a)

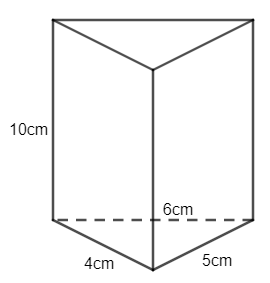Chu vi đáy là: 4 + 5 + 6 =15 (cm)

Diện tích xung quanh hình lăng trụ đứng tam giác là:

15.10 = 150 (cm²)

Vậy diện tích xung quanh hình lăng trụ đứng tam giác là 150 cm².

b)

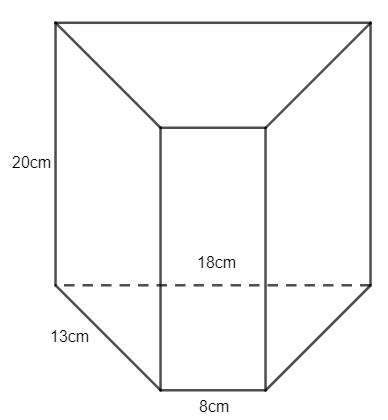Diện tích một đáy hình lăng trụ đứng đã cho là:

$\frac{1}{2}\left(8+18\right).12=\frac{1}{2}\mathrm{.26.12}=156\left(c{m}^2\right)$

Chu vi đáy là: 13 + 13 + 8 + 18 = 52 (cm)

Diện tích xung quanh của hình lăng trụ đứng đã cho là:

52.20 = 1040 (cm²)

Diện tích toàn phần hình lăng trụ đứng đã cho là:

156.2 + 1040 = 1352 (cm²).

Vậy diện tích toàn phần hình lăng trụ đứng đã cho là 1352 cm².

Bài 3 trang 87 Toán lớp 7 Tập 1:

a) Một hình lập phương có độ dài cạnh là 3 cm. Tính thể tích của hình lập phương đó.

b) Một hình lập phương mới có độ dài cạnh gấp đôi độ dài cạnh của hình lập phương ban đầu. Tính thể tích của hình lập phương mới và cho biết thể tích của hình lập phương mới gấp bao nhiêu lần thể tích của hình lập phương ban đầu.

Lời giải:

a) Thể tích hình lập phương với độ dài cạnh là 3 cm là:

V = 3.3.3 = 27 (cm³)

Vậy thể tích hình lập phương đó là 27 cm³.

b) Gọi độ dài cạnh hình vuông ban đầu là x (x > 0)

Vì độ dài cạnh hình vuông mới gấp 2 lần độ dài cạnh hình vuông ban đầu nên độ dài cạnh hình vuông mới là 2x.

Thể tích hình lập phương ban đầu là: V₁ = x³

Thể tích hình lập phương mới là: V₂ = (2x)³ = 8x³.

Thể tích của hình lập phương mới gấp số lần thể tích hình lập phương cũ là:

V₂:V₁ = (8x³) : x³ = 8 (lần).

Vậy thể tích hình lập phương mới gấp 8 lần thể tích hình lập phương cũ.

Bài 4 trang 87 Toán lớp 7 Tập 1: Hình 34 mô tả một xe chở hai bánh mà thùng chứ của nó có dạng lăng trụ đứng tam giác với các kích thước cho trên. Hỏi thùng chứa của xe chở hai bánh có kích thước là bao nhiêu?

Lời giải:

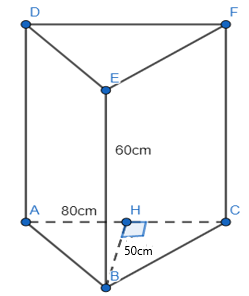Ta có:

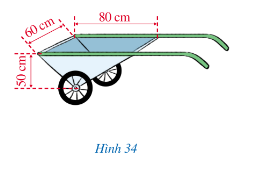
Diện tích đáy thùng chứa của xe là:

$\frac{1}{2}BH.AC=\frac{1}{2}\mathrm{.50.80}=2000\left(c{m}^2\right)$

Thể tích thùng chứa của xe là:

V = S.h = 2 000.60 = 120 000 (cm³).

Vậy thể tích thùng chứa của xe là 120 000 cm³.

Bài 5 trang 87 Toán lớp 7 Tập 1: Một ngôi nhà có cấu trúc và kích thước như Hình 35.

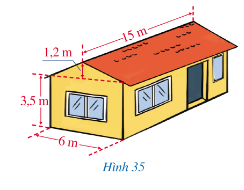Tính thể tích phần không gian được giới hạn bởi ngôi nhà đó.

Hướng dẫn: Phần không gian của ngôi nhà đó có thể chia thành 2 phần: phần không gian có dạng một hình hộp chữ nhật và phần không gian còn lại có dạng một hình lăng trụ đứng tam giác.

Lời giải:

Thể tích phần không gian của ngôi nhà có dạng hình hộp chữ nhật là:

V₁ = 3,5.6.15 = 315 (m³)

Diện tích đáy phần không gian mái nhà có hình lăng trụ đứng là:

S = $\frac{1}{2}.1,2.6=3,6\left(m^2\right)$

Thể tích phần không gian có hình lăng trụ đứng là:

$v_2=3,6.15=54\left(c{m}^3\right)$

Thể tích phần không gian ngôi nhà đã chiếm chỗ là:

54 + 315 = 369 (cm³).

Vậy thể tích phần không gian được giới hạn bởi ngôi nhà đó là 369 m³.

Lý thuyết Toán 7 Bài tập ôn tập chương 3 - Cánh diều

1. Hình hộp chữ nhật. Hình lập phương.

1.1 Hình hộp chữ nhật

- Hình hộp chữ nhật có 6 mặt, 12 cạnh, 8 đỉnh, 4 đường chéo.

- Các mặt đều là hình chữ nhật.

- Các cạnh bên bằng nhau.

Chú ý: Để nhận dạng tốt hơn hình hộp chữ nhật, người ta vẽ các cạnh không nhìn thấy bằng nét đứt.

1.2. Hình lập phương

- Hình lập phương có 6 mặt, 12 cạnh, 8 đỉnh, 4 đường chéo.

- Các mặt đều là hình vuông.

- Các cạnh đều bằng nhau.

1.3. Diện tích xung quanh và thể tích của hình hộp chữ nhật và hình lập phương

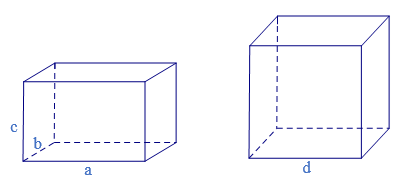
Cho hình hộp chữ nhật có ba kích thước: chiều dài a, chiều rộng là b, chiều cao là c (a, b, c cùng đơn vị đo). Cho hình lập phương có độ dài cạnh là d.

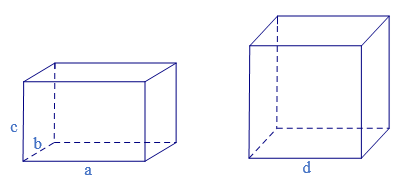
Ta có một số công thức sau:

2. Hình lăng trụ đứng tam giác. Hình lăng trụ đứng tứ giác
2.1 Hình lăng trụ đứng tam giác

- Hình lăng trụ đứng tam giác có 5 mặt, 9 cạnh, 6 đỉnh.

- Hai mặt đáy cùng là tam giác và nằm trong hai mặt phẳng song song với nhau; Mỗi mặt bên là hình chữ nhật;

- Các cạnh bên bằng nhau;

- Chiều cao của hình lăng trụ đứng tam giác là độ dài cạnh bên.

2.2. Hình lăng trụ đứng tứ giác

- Lăng trụ đứng tứ giác có 6 mặt, 12 cạnh, 8 đỉnh.

- Hai mặt đáy cùng là tứ giác và song song với nhau. Mỗi mặt bên là hình chữ nhật.

- Các cạnh bên bằng nhau.

- Chiều cao của hình lăng trụ đứng tứ giác là độ dài một cạnh bên.

Chú ý: Hình hộp chữ nhật và hình lập phương cũng là lăng trụ đứng tứ giác.

2.3. Thể tích và diện tích xung quanh của hình lăng trụ đứng tam giác, lăng trụ đứng tứ giác

- Thể tích của hình lăng trụ đứng tứ giác bằng diện tích đáy nhân với chiều cao.

Tức là: V = S . h, trong đó V là thể tích, S là diện tích đáy và h là chiều cao của hình lăng trụ đứng tứ giác.

- Thể tích của hình lăng trụ đứng tam giác bằng diện tích đáy nhân với chiều cao.

Tức là: V = S . h, trong đó V là thể tích, S là diện tích đáy và h là chiều cao của hình lăng trụ đứng tam giác.

- Diện tích xung quanh của hình lăng trụ đứng tam giác hay hình lăng trụ đứng tứ giác bằng chu vi đáy nhân với chiều cao.

Tức là S_xq = C . h, trong đó S_xq là diện tích xung quanh, C là chu vi đáy, h là chiều cao của hình lăng trụ đứng tam giác hay của hình lăng trụ đứng tứ giác.

Xem thêm lời giải bài tập Toán lớp 7 Cánh diều hay, chi tiết khác:

Bài 2: Hình lăng trụ đứng tam giác. Hình lăng trụ đứng tứ giác

Bài 1: Góc ở vị trí đặc biệt

Bài 2: Tia phân giác của một góc

Bài 3: Hai đường thẳng song song

Bài 4: Định lý