Giải Toán 7 Bài 5 (Cánh diều): Phép chia đa thức một biến

Giải bài tập Toán 7 Bài 5: Phép chia đa thức một biến

A. Câu hỏi

Giải Toán 7 trang 64 Tập 2

Câu hỏi khởi động trang 64 Toán 7 Tập 2:

Trong quá trình biến đổi và tính toán những biểu thưc đại số, nhiều khi ta phải thực hiện phép chia một đa thức (một biến) cho một đa thức (một biến) khác, chẳng hạn ta cần thực hiện phép chia sau: (x³ + 1) : (x² – x +1).

Làm thế nào để thực hiện được phép chia một đa thức cho một đa thức khác?

Lời giải:

Sau bài học này chúng ta sẽ giải quyết được câu hỏi trên như sau:

Muốn chia một đa thức P cho một đa thức Q khác đa thức không (cả hai đa thức đều đã thu gọn và sắp xếp các đơn thức theo số mũ giảm dần của biến) khi bậc của đa thức bị chia P lớn hơn hoặc bằng bậc của đa thức chia Q, ta làm như sau:

Bước 1:

- Chia đơn thức bậc cao nhất của đa thức P cho đơn thức bậc cao nhất của đa thức Q;

- Nhân kết quả trên với đa thức Q và đặt tích dưới đa thức P sao cho hai đơn thức có cùng số mũ của biến ở cùng cột;

- Lấy đa thức P trừ đi tích đặt dưới để được đa thức bị chia mới.

Bước 2: Tiếp tục quá trình trên cho đến khi nhận được đa thức không hoặc đa thức có bậc nhỏ hơn bậc của đa thức chia.

Hoạt động 1 trang 64 Toán 7 Tập 2: Thực hiện phép tính:

a) x⁵ : x³;

b) (4x³) : x²;

c) (ax^m) : (bxⁿ) (a ≠ 0; b ≠ 0; m, n ∈ ℕ; m ≥ n).

Lời giải:

a) x⁵ : x³ = x^5-3 = x².

b) (4x³) : x² = 4 . (x³ : x²) = 4 . x^3-2 = 4x.

c) (ax^m) : (bxⁿ) = $\frac{a}{b}.\left(x^m:x^n\right)=\frac{a}{b}.x^{m-n}$ (a ≠ 0; b ≠ 0; m, n ∈ ℕ; m ≥ n).

Luyện tập 1 trang 64 Toán 7 Tập 2: Tính:

a) (3x⁶) : (0,5x⁴);

b) (-12x^m+2) : (4xⁿ⁺²) (m, n ∈ ℕ; m ≥ n).

Lời giải:

a) (3x⁶) : (0,5x⁴) = (3 : 0,5) . (x⁶ : x⁴) = 6x².

b) (-12x^m+2) : (4xⁿ⁺²)

= (-12 : 4) . (x^m+2 : xⁿ⁺²)

= -3 . x^m+2-(n+2)

= -3 . x^m+2-n-2

= -3x^m-n (m, n ∈ ℕ; m ≥ n).

Hoạt động 2 trang 64 Toán 7 Tập 2:

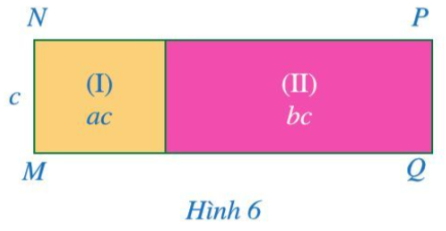
Ở Hình 6, diện tích các hình chữ nhật (I), (II) lần lượt là A = ac, B = bc. Biết MN = c.

a) Tính NP.

b) So sánh: (A + B) : c và A : c + B : c.

Lời giải:

a) Hình chữ nhật (I) có độ dài cạnh kề với cạnh MN là A : c = ac : c = a.

Hình chữ nhật (II) có độ dài cạnh kề với cạnh PQ là B : c = bc : c = b.

Khi đó độ dài cạnh NP là NP = a + b.

b) Ta có:

- Diện tích hình chữ nhật MNPQ bằng tổng diện tích hai hình chữ nhật (I) và (II) là:

ac + bc = A + B

- Độ dài cạnh NP là NP = (ac + bc) : c = (A + B) : c.

Mà NP = a + b = A : c + B : c.

Vậy (A + B) : c = A : c + B : c.

Giải Toán 7 trang 65 Tập 2

Hoạt động 3 trang 65 Toán 7 Tập 2:

Cho đa thức P(x) = 4x² + 3x và đơn thức Q(x) = 2x.

a) Hãy chia từng đơn thức (của biến x) có trong đa thức P(x) cho đơn thức Q(x).

b) Hãy cộng các thương vừa tìm được.

Lời giải:

a) Ta có:

- Đơn thức có trong đa thức P(x) là: 4x²; 3x.

- Đơn thức có trong đa thức Q(x) là: 2x.

Chia từng đơn thức (của biến x) có trong đa thức P(x) cho đơn thức Q(x) ta được:

4x² : 2x = (4 : 2) . (x² : x) = 2x.

3x : 2x = (3 : 2) . (x : x) = $\frac{3}{2}$.

b) Cộng các thương vừa tìm được ta có:

4x² : 2x + 3x : 2x = 2x + $\frac{3}{2}$.

Luyện tập 2 trang 65 Toán 7 Tập 2: Tính:

$\left(\frac{1}{2}{x}^4-\frac{1}{4}{x}^3+x\right):\left(-\frac{1}{8}x\right)$.

Lời giải:

$\left(\frac{1}{2}{x}^4-\frac{1}{4}{x}^3+x\right):\left(-\frac{1}{8}x\right)$

$=\frac{1}{2}{x}^4:\left(-\frac{1}{8}x\right)-\frac{1}{4}{x}^3:\left(-\frac{1}{8}x\right)+x:\left(-\frac{1}{8}x\right)$

$=\frac{1}{2}{x}^4:\left(\frac{-1}{8}x\right)-\frac{1}{4}{x}^3:\left(\frac{-1}{8}x\right)+x:\left(\frac{-1}{8}x\right)$

$=\left(\frac{1}{2}:\frac{-1}{8}\right).\left(x^4:x\right)-\left(\frac{1}{4}:\frac{-1}{8}\right).\left(x^3:x\right)+\left(1:\frac{-1}{8}\right).\left(x:x\right)$

$=\left(\frac{1}{2}.\frac{8}{-1}\right).x^3-\left(\frac{1}{4}.\frac{8}{-1}\right).x^2+\left(1.\frac{8}{-1}\right).1$

$=\frac{8}{-2}.x^3-\frac{8}{-4}.x^2+\left(-8\right)$

= -4x³ – (−2x²) - 8.

= -4x³ + 2x² - 8.

Hoạt động 4 trang 65 Toán 7 Tập 2: Thực hiện phép chia:

a) (2x² + 5x + 2) : (2x + 1);

b) (3x³ - 5x² + 2) : (x² + 1).

Lời giải:

a) Để thực hiện phép chia đa thức ta làm như sau:

- Lấy 2x² chia cho 2x được x, viết x;

Lấy x nhân với 2x + 1 được 2x² + x, viết 2x² + x;

Lấy 2x² + 5x + 2 trừ đi 2x² + x được 4x + 2, viết 4x + 2.

- Lấy 4x chia cho 2x được 2, viết 2;

Lấy 2 nhân với 2x + 1 được 4x + 2, viết 4x + 2;

Lấy 4x + 2 trừ 4x + 2 được 0, viết 0.

Ta có phép tính như sau:

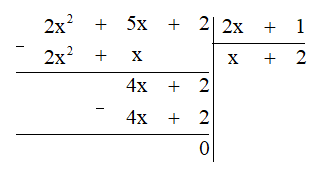
Vậy (2x² + 5x + 2) : (2x + 1) = x + 2.

b) Để thực hiện phép chia đa thức ta làm như sau:

- Lấy 3x³ chia cho x² được 3x, viết 3x;

Lấy 3x nhân với x² + 1 được 3x³ + 3x, viết 3x³ + 3x;

Lấy 3x³ - 5x² + 2 trừ đi 3x³ + 3x được -5x² - 3x + 2, viết -5x² - 3x + 2.

- Lấy -5x² chia cho x² được -5, viết -5;

Lấy -5 nhân với x² + 1 được -5x² - 5, viết -5x² - 5;

Lấy -5x² - 3x + 2 trừ đi -5x² - 5 được -3x + 7, viết -3x + 7.

Ta thấy bậc của đa thức -3x + 7 (bằng 1), nhỏ hơn bậc của đa thức chia x² + 1 (bằng 2) nên phép chia không thể tiếp tục được.

Ta có phép tính như sau:

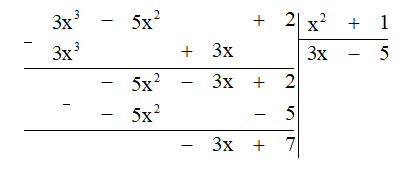
Do đó (3x³ - 5x² + 2) : (x² + 1) = 3x – 5 (dư -3x + 7).

Hay 3x³ - 5x² + 2 = (3x - 5).(x² + 1) + (-3x + 7).

Giải Toán 7 trang 66 Tập 2

Luyện tập 3 trang 66 Toán 7 Tập 2: Tính:

a) (x³ + 1) : (x² - x + 1);

b) (8x³ - 6x² + 5) : (x² + x + 1).

Lời giải:

a) Thực hiện phép chia đa thức ta được:

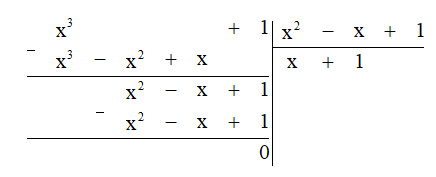
Vậy (x³ + 1) : (x² - x + 1) = x + 1.

b) Thực hiện phép chia đa thức ta được:

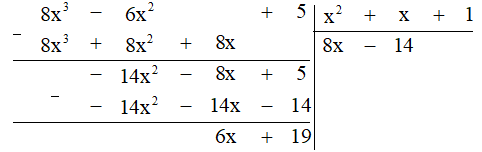
Vậy (8x³ - 6x² + 5) : (x² + x + 1) = 8x – 14 (dư 6x + 19).

Hay 8x³ - 6x² + 5 = (8x - 14) . (x² + x + 1) + (6x + 19).

B. Bài tập

Giải Toán 7 trang 67 Tập 2

Bài 1 trang 67 Toán 7 Tập 2: Tính:

a) (4x³) : (-2x²);

b) (-7x²) : (6x);

c) (-14x⁴) : (-8x³).

Lời giải:

a) (4x³) : (-2x²) = [4 : (-2)] . (x³ : x²) = (-2).x^3-2 = −2x.

b) (-7x²) : (6x) = (-7 : 6) . (x² : x) = $\frac{-7}{6}$x^2-1 $=\frac{-7}{6}x.$

c) (14x⁴) : (-8x³) = [(-14) : (-8)] . (x⁴ : x³) $=\frac{-14}{8}{x}^{4-3}=\frac{-7}{4}x.$

Bài 2 trang 67 Toán 7 Tập 2: Tính:

a) (8x³ + 2x² - 6x) : (4x);

b) (5x³ - 4x) : (-2x);

c) (-15x⁶ - 24x³) : (-3x²).

Lời giải:

a) (8x³ + 2x² - 6x) : (4x)

= (8x³ : 4x) + (2x² : 4x) - (6x : 4x)

$=2.x^{3-1}+\frac{2}{4}.x^{2-1}-\frac{6}{4}.x^{1-1}$

= 2x² + $\frac{1}{2}$x - $\frac{3}{2}$.

Vậy (8x³ + 2x² - 6x) : (4x) $=2x^2+\frac{1}{2}x-\frac{3}{2}.$

b) (5x³ - 4x) : (-2x)

= [5x³ : (-2x)] - [4x : (-2x)]

$=\frac{5}{-2}.x^{3-1}-\frac{4}{-2}{x}^{1-1}$

$=\frac{-5}{2}{x}^2-\left(-2\right)x^0$

= $\frac{-5}{2}$x² - (-2)

= $\frac{-5}{2}$x² + 2.

Vậy (5x³ - 4x) : (-2x) = $\frac{-5}{2}$x² + 2.

c) (-15x⁶ - 24x³) : (-3x²)

= [(-15x⁶) : (-3x²)] - [24x³ : (-3x²)]

= [(-15) : (-3)].x^6-2 – [24 : (-3)].x^3-2

= 5x⁴ - (-8).x

= 5x⁴ + 8x.

Vậy (-15x⁶ - 24x³) : (-3x²) = 5x⁴ + 8x.

Bài 3 trang 67 Toán 7 Tập 2: Tính:

a) (x² - 2x + 1) : (x - 1);

b) (x³ + 2x² + x) : (x² + x);

c) (-16x⁴ + 1) : (-4x² + 1);

d) (-32x⁵ + 1) : (-2x + 1).

Lời giải:

a) Thực hiện phép chia đa thức ta được:

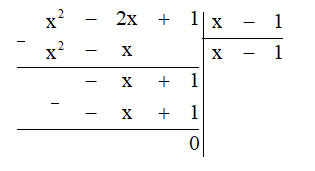
Vậy (x² - 2x + 1) : (x - 1) = x - 1.

b) Thực hiện phép chia đa thức ta được:

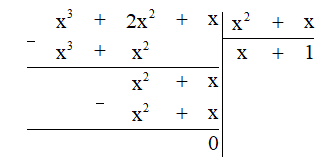
Vậy (x³ + 2x² + x) : (x² + x) = x + 1.

c) Thực hiện phép chia đa thức ta được:

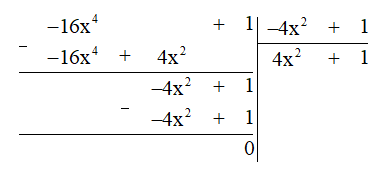
Vậy (-16x⁴ + 1) : (-4x² + 1) = 4x² + 1.

d) Thực hiện phép tính ta được:

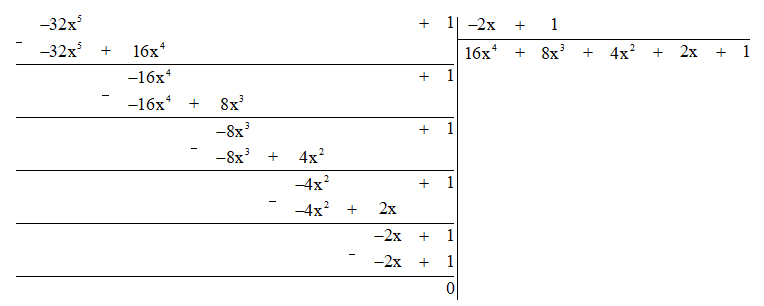
Vậy (-32x⁵ + 1) : (-2x + 1) = 16x⁴ + 8x³ + 4x² + 2x + 1.

Bài 4 trang 67 Toán 7 Tập 2: Tính:

a) (6x² - 2x + 1) : (3x - 1);

b) (27x³ + x² - x + 1) : (-2x + 1);

c) (8x³ + 2x² + x) : (2x³ + x + 1);

d) (3x⁴ + 8x³ - 2x² + x + 1) : (3x + 1).

Lời giải:

a) Thực hiện phép chia đa thức ta được:

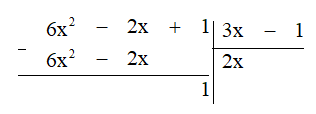
Vậy (6x² - 2x + 1) : (3x - 1) = 2x (dư 1).

Hay 6x² - 2x + 1 = 2x . (3x - 1) + 1.

b) Thực hiện phép chia đa thức ta được:

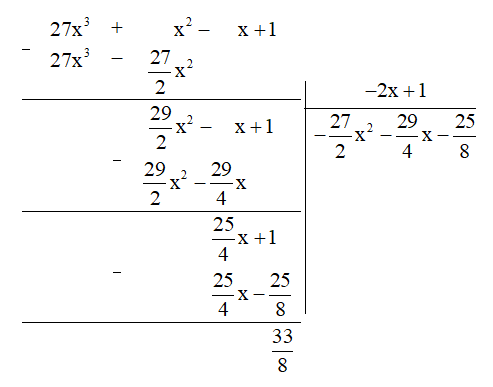
Vậy (27x³ + x² - x + 1) : (-2x + 1) = $\frac{-27}{2}{x}^2-\frac{29}{4}x-\frac{25}{8}$ (dư $\frac{33}{8})$

Hay 27x³ + x² - x + 1 = $\left(\frac{-27}{2}{x}^2-\frac{29}{4}x-\frac{25}{8}\right)$ . (-2x + 1) + $\frac{33}{8}$.

c) Thực hiện phép chia đa thức ta được:

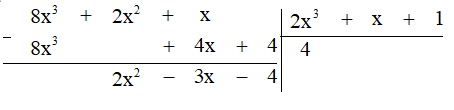
Vậy (8x³ + 2x² + x) : (2x³ + x + 1) = 4 (dư 2x² -3x - 4).

Hay 8x³ + 2x² + x = 4(2x³ + x + 1) + (2x² -3x - 4).

d) Thực hiện phép chia đa thức ta được:

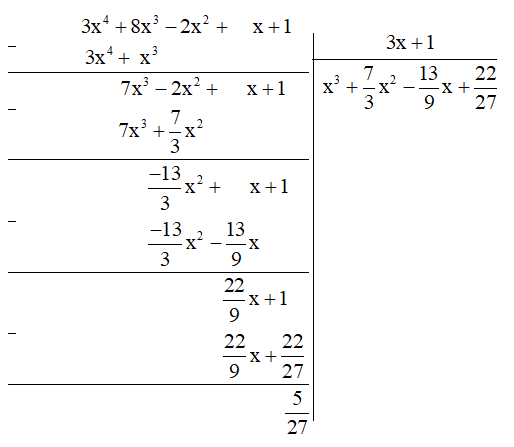
Vậy (3x⁴ + 8x³ - 2x² + x + 1) : (3x + 1) = $x^3+\frac{7}{3}{x}^2-\frac{13}{9}x+\frac{22}{27}$ (dư $\frac{5}{27}$)

Hay 3x⁴ + 8x³ - 2x² + x + 1 = $\left(x^3+\frac{7}{3}{x}^2-\frac{13}{9}x+\frac{22}{27}\right)$(3x + 1) + $\frac{5}{27}$

Bài 5 trang 67 Toán 7 Tập 2:

Một công ty sau khi tăng giá 30 nghìn đồng mỗi sản phẩm so với giá ban đầu là 2x (nghìn đồng) thì có doanh thu là 6x² + 170x + 1 200 (nghìn đồng). Tính số sản phẩm mà công ty đó đã bán được theo x.

Lời giải:

Giá sản phẩm ban đầu là 2x (nghìn đồng)

Sau khi tăng giá 30 nghìn đồng thì giá sản phẩm lúc này là 2x + 30 (nghìn đồng).

Doanh thu là 6x² + 170x + 1 200 (nghìn đồng), do đó số sản phẩm mà công ty đó bán được là: (6x² + 170x + 1 200) : (2x + 30)

Thực hiện phép chia đa thức ta được:

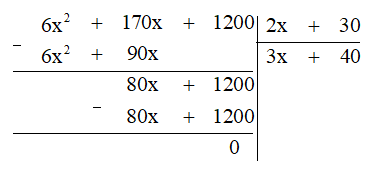
Khi đó (6x² + 170x + 1 200) : (2x + 30) = 3x + 40.

Vậy công ty đó đã bán được 3x + 40 sản phẩm.

Bài 6 trang 67 Toán 7 Tập 2:

Một hình hộp chữ nhật có thể tích là x³ + 6x² + 11x + 6 (cm³). Biết đáy là hình chữ nhật có các kích thước là x + 1 (cm) và x + 2 (cm). Tính chiều cao của hình hộp chữ nhật đó theo x.

Lời giải:

Đáy của hình hộp chữ nhật là hình chữ nhật có các kích thước là x + 1 (cm) và x + 2 (cm) nên diện tích đáy của hình hộp chữ nhật là:

(x + 1).(x + 2) = x.x + x.2 + 1.x + 1.2 = x² + 2x + x + 2 = x² + 3x + 2 (cm²).

Hình hộp chữ nhật có thể tích là x³ + 6x² + 11x + 6 (cm³) nên chiều cao của hình hộp chữ nhật là: (x³ + 6x² + 11x + 6) : (x² + 3x + 2)

Thực hiện phép chia đa thức ta được:

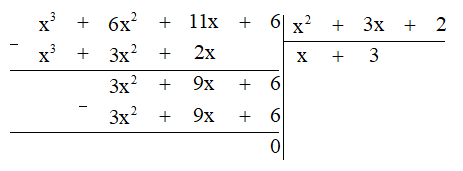
Khi đó (x³ + 6x² + 11x + 6) : (x² + 3x + 2) = x + 3.

Vậy chiều cao của hình hộp chữ nhật đó là x + 3 cm.

Lý thuyết Toán 7 Bài 5. Phép chia đa thức một biến - Cánh diều

1. Chia đơn thức cho đơn thức

Muốn chia đơn thức A cho đơn thức B (B ≠ 0) khi số mũ của biến trong A lớn hơn hoặc bằng số mũ của biến đó trong B, ta làm như sau:

+ Chia hệ số của đơn thức A cho hệ số của đơn thức B.

+ Chia luỹ thừa của biến trong A cho luỹ thừa của biến đó trong B.

+ Nhân các kết quả vừa tìm được với nhau.

Tổng quát: Với a ≠ 0; b ≠ 0, m, n ∈ ℕ, m ≥ n ta có:

(ax^m) : (bxⁿ) = $\frac{\mathrm{a}}{\mathrm{b}}$.(x^m : xⁿ) = $\frac{\mathrm{a}}{\mathrm{b}}$.x^{m – n}

Ví dụ: Tính:

a) 14x² : 7x;

b) 3x⁶ : 2x²;

c) –5yⁿ : 10y² (với n ∈ ℕ, n > 2);

d) (–20x^{m + 1}) : (5x^{n + 1}) (với m, n ∈ ℕ, m > n).

Hướng dẫn giải

a) 14x² : 7x = (14 : 7). (x² : x) = 2x^{2 – 1} = 2x;

b) 3x⁶ : 2x² = $\frac{3}{2}.$x^{6 – 2} = $\frac{3}{2}.$x⁴;

c) Với n ∈ ℕ, n > 2 ta có:

–5yⁿ : 10y² = $\frac{-5}{10}$.y^{n – 2} = $-\frac{1}{2}$y^{n – 2}.

d) Với m, n ∈ ℕ, m > n ta có:

(–20x^{m + 1}) : (5x^{n + 1})

= (–20 : 5). (x^{m + 1} : x^{n + 1})

= –4x^{m + 1 – n – 1} = –4x^{m – n}.

2. Chia đa thức cho đơn thức

Muốn chia đa thức P cho đơn thức Q (Q ≠ 0) khi số mũ của biến ở mỗi đơn thức của P lớn hơn hoặc bằng số mũ của biến đó trong Q, ta chia mỗi đơn thức của đa thức P cho đơn thức Q rồi cộng các thương với nhau.

(A + B) : C = A : C + B : C

(A – B) : C = A : C – B : C

Ví dụ: Tính

a) (20x⁵ – 18x⁴ + 6x² – 4x) : (–2x);

b) (45x⁵ + 10x³ – 5x²) : 5x².

Hướng dẫn giải

a) (20x⁵ – 18x⁴ + 6x² – 4x) : (–2x)

= 20x⁵ : (–2x) – 18x⁴ : (–2x) + 6x² : (–2x) – 4x : (–2x)

= [20 : (–2)](x⁵ : x) – [18 : (–2)](x⁴ : x) + [6 : (–2)](x² : x) – [4 : (–2)](x : x)

= –10x⁴ + 9x³ – 3x + 2.

b) (45x⁵ + 10x³ – 5x²) : 5x²

= 45x⁵ : 5x² + 10x³ : 5x² – 5x² : 5x²

= (45 : 5)(x⁵ : x²) + (10 : 5)(x³ : x²) – (5 : 5)(x² : x²)

= 9x³ + 2x – 1.

3. Chia đa thức một biến đã sắp xếp

* Để chia một đa thức cho một đa thức khác đa thức không (cả hai đa thức đều đã thu gọn và sắp xếp các đơn thức theo số mũ giảm dần của biến) khi bậc của đa thức bị chia lớn hơn hoặc bằng bậc của đa thức chia, ta làm như sau:

– Bước 1.

+ Chia đơn thức bậc cao nhất của đa thức bị chia cho đơn thức bậc cao nhất của đa thức chia.

+ Nhân kết quả trên với đa thức chia và đặt tích dưới đa thức bị chia sao cho hai đơn thức có cùng số mũ của biến ở cùng cột.

+ Lấy đa thức bị chia trừ đi tích đặt dưới để được đa thức mới.

– Bước 2. Tiếp tục quá trình trên cho đến khi nhận được đa thức không hoặc đa thức

có bậc nhỏ hơn bậc của đa thức chia.

* Nhận xét

– Khi chia đa thức A cho đa thức B của cùng một biến (B ≠ 0), có hai khả năng xảy ra:

+ Phép chia có dư bằng 0. Trong trường hợp này ta nói đa thức A chia hết cho đa thức B.

+ Phép chia có dư là đa thức R (R ≠ 0) với bậc của R nhỏ hơn bậc của B. Phép chia trong trường hợp này được gọi là phép chia có dư.

– Người ta chứng minh được rằng đối với hai đa thức tuỳ ý A và B của cùng một biến (B ≠ 0), tồn tại duy nhất một cặp đa thức Q và R sao cho A = B . Q + R, trong đó R bằng 0 hoặc bậc của R nhỏ hơn bậc của B. Như vậy, đã thức A chia hết cho đa thức B khi và chỉ khi R = 0.

Ví dụ: Tính:

a) (9x³ + 6x² + 3x – 3) : (3x + 1)

b) (6x² + 4) : (– 2x – 1)

Hướng dẫn giải

a) Ta thực hiện đặt tính chia đa thức như sau:

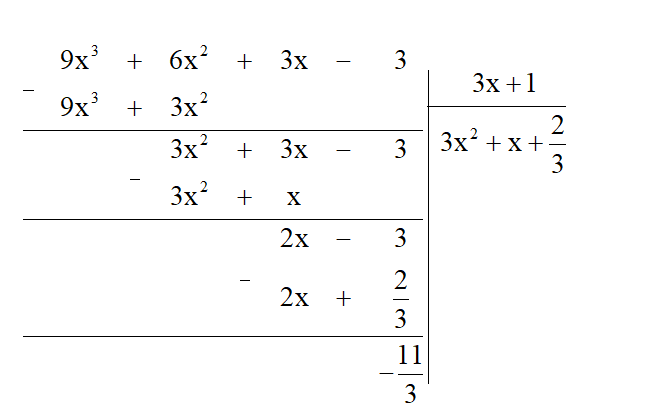
Vậy (9x³ + 6x² + 3x – 3) : (3x + 1) = 3x² + x + $\frac{3}{2}$(dư $\frac{-11}{3}$).

b) Ta thực hiện đặt tính chia đa thức như sau:

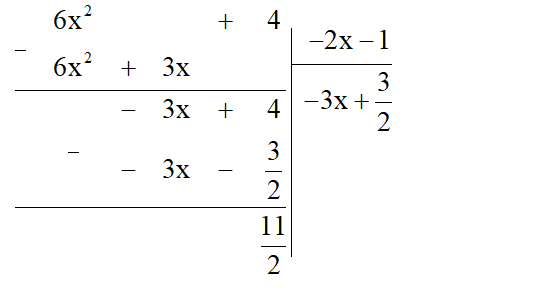
Vậy (6x² + 4) : (–2x – 1) = $-3\text{x}+\frac{3}{2}$ (dư $\frac{11}{2}$).

Xem thêm lời giải bài tập Toán lớp 7 Cánh diều hay, chi tiết khác:

Bài tập cuối chương 6

Bài 1: Tổng các góc của một tam giác

Bài 2: Quan hệ giữa góc và cạnh đối diện. Bất đẳng thức tam giác

Bài 3: Hai tam giác bằng nhau

Bài 4: Trường hợp bằng nhau thứ nhất của tam giác: cạnh – cạnh – cạnh