Toán 7 Bài 1 (Cánh diều): Tập hợp Q các số hữu tỉ

Giải bài tập Toán 7 Bài 1: Tập hợp Q các số hữu tỉ

Bài giảng Toán 7 Bài 1: Tập hợp Q các số hữu tỉ

Giải Toán 7 trang 5 Tập 1

Hoạt động khởi động

Khởi động trang 5 Toán lớp 7 Tập 1: Nhiệt độ lúc 13 giờ ngày 24/01/2016 tại một số trạm đo được cho bởi bảng sau:

Các số chỉ nhiệt độ nêu trên có viết được dưới dạng phân số không?

Lời giải:

Ta có $-1,3=\frac{-13}{10}$; $-0,5=-\frac{5}{10}$;

$0,3=\frac{3}{10}$; $-3,1=\frac{-31}{10}$.

Vậy các số chỉ nhiệt độ −1,3 ^oC; −0,5 ^oC; 0,3 ^oC; −3,1 ^oC viết được dưới dạng phân số.

1. Số hữu tỉ

Hoạt động 1 trang 5 Toán lớp 7 Tập 1: Viết các số $-3;\mathrm{0,5};2\frac{3}{7}$ dưới dạng phân số.

Lời giải:

Ta có9

–3 có thể viết dưới dạng phân số là $\frac{-3}{1}$;

0,5 có thể viết dưới dạng phân số là $\frac{5}{10}$;

$2\frac{3}{7}$ có thể viết dưới dạng phân số là $\frac{17}{7}$

Vậy các số $-3;\mathrm{0,5};2\frac{3}{7}$ viết được dưới dạng phân số lần lượt là:$\frac{-3}{1};\frac{5}{10};\frac{17}{7}$ .

Giải Toán 7 trang 6 Tập 1

Luyện tập 1 trang 6 Toán lớp 7 Tập 1: Các số 21 ; −12; $\frac{-7}{-9}$ ; −4,7; −3,05 có là số hữu tỉ không? Vì sao?

Lời giải:

Ta có:

Số 21 là số hữu tỉ vì nó có thể viết được dưới dạng phân số $\frac{a}{b}\left(21=\frac{21}{1}\right)$ với a, b ∈ ℤ và b ≠ 0;

Số –12 là số hữu tỉ vì nó có thể viết được dưới dạng phân số $\frac{a}{b}\left(-12=\frac{-12}{1}\right)$ với a,b ∈ ℤ và b ≠ 0;

Số $\frac{-7}{-9}$ là số hữu tỉ vì nó viết được dưới dạng $\frac{a}{b}$ với a, b ∈ ℤ và b ≠ 0;

Số –4,7 là số hữu tỉ vì nó viết được dưới dạng phân số $\frac{a}{b}\left(-4,7=\frac{-47}{10}\right)$ với a, b ∈ ℤ và b ≠ 0;

Số –3,05 là số hữu tỉ vì nó viết được dưới dạng phân số $\frac{a}{b}\left(-3,05=\frac{-305}{100}\right)$ với a, b ∈ ℤ và b ≠ 0;

Vậy các số $21;-12;\frac{-7}{-9};-4,7;-3,05$ là số hữu tỉ.

2. Biểu diễn số hữu tỉ trên trục số

Hoạt động 2 trang 6 Toán lớp 7 Tập 1: Biểu diễn số hữu tỉ $\frac{7}{10}$ trên trục số

Lời giải:

Để biểu diễn số hữu tỉ $\frac{7}{10}$ trên trục số, ta làm như sau (xem Hình 1):

• Chia đoạn thẳng đơn vị (chẳng hạn đoạn từ điểm 0 đến điểm 1) thành mười phần bằng nhau, lấy một đoạn làm đơn vị mới (đơn vị mới bằng $\frac{1}{10}$ đơn vị cũ);

• Đi theo chiều dương của trục số, bắt đầu từ điểm 0, ta lấy ra 7 đơn vị mới đến điểm A. Điểm A biểu diễn số hữu tỉ $\frac{7}{10}$.

Giải Toán 7 trang 7 Tập 1

Luyện tập 2 trang 7 Toán lớp 7 Tập 1: Biểu diễn số hữu tỉ − 0,3 trên trục số.

Lời giải:

Ta có: $-\mathrm{0,3}=\frac{-3}{10}$.

Ta biểu diễn số hữu tỉ $\frac{-3}{10}$ trên trục số như sau:

• Chia đoạn thẳng đơn vị (chẳng hạn đoạn từ điểm 0 đến điểm –1) thành mười phần bằng nhau, lấy một đoạn làm đơn vị mới (đơn vị mới bằng $\frac{1}{10}$ đơn vị cũ);

• Đi theo chiều âm của trục số, bắt đầu từ điểm 0, ta lấy ra 3 đơn vị mới đến điểm A. Điểm A biểu diễn số hữu tỉ $\frac{-3}{10}$ hay chính là –0,3.

3. Số đối của một số hữu tỉ

Hoạt động 3 trang 7, 8 Toán lớp 7 Tập 1: Quan sát hai điểm biểu diễn các số hữu tỉ $\frac{-5}{4}$ và $\frac{5}{4}$ trên trục số sau (Hình 4):

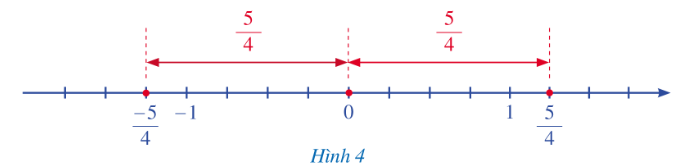
Nêu nhận xét về khoảng cách từ hai điểm $\frac{-5}{4}$ và $\frac{5}{4}$ đến điểm gốc 0.

Lời giải:

Dựa vào hình vẽ trên, ta thấy:

• Khoảng cách từ điểm $\frac{-5}{4}$ đến điểm gốc 0 là $\frac{5}{4}$ đơn vị;

• Khoảng cách từ điểm $\frac{5}{4}$ đến điểm gốc 0 là $\frac{5}{4}$ đơn vị.

Nhận thấy hai khoảng cách trên đều bằng $\frac{5}{4}$ đơn vị.

Vậy khoảng cách từ hai điểm $\frac{-5}{4}$ và $\frac{5}{4}$ đến điểm gốc 0 bằng nhau.

Giải Toán 7 trang 8 Tập 1

Luyện tập 3 trang 8 Toán lớp 7 Tập 1: Tìm số đối của mỗi số sau: $\frac{2}{9}; -0,5$

Lời giải:

Số đối của $\frac{2}{9}$ là $\frac{-2}{9}$.

Số đối của − 0,5 là − (−0,5) = 0,5.

4. So sánh các số hữu tỉ

Giải Toán 7 trang 9 Tập 1

Hoạt động 4 trang 9 Toán lớp 7 Tập 1: So sánh:

a) $-\frac{1}{3}$ và $\frac{-2}{5}$;

b) 0,125 và 0,13;

c) – 0,6 và $\frac{-2}{3}$.

Lời giải:

a) Ta có $-\frac{1}{3}=\frac{-1}{3}=\frac{\left(-1\right).5}{3.5}=\frac{-5}{15}$;$\frac{-2}{5}=\frac{\left(-2\right).3}{5.3}=\frac{-6}{15}$

Vì − 5 > − 6 nên $\frac{-5}{15}>\frac{-6}{15}$ hay $\frac{-1}{3}>\frac{-2}{5}$.

Vậy $-\frac{1}{3}>\frac{-2}{5}$.

b) Ta đi so sánh hai số thập phân.

Kể từ trái sang phải cặp chữ số cùng hàng đầu tiên khác nhau là cặp chữ số hàng phần trăm.

Mà 3 > 2 nên 0,125 < 0,13.

Vậy 0,125 < 0,13.

c) Ta có –0,6 = $\frac{-3}{5}=\frac{\left(-3\right).3}{5.3}=\frac{-9}{15}$;$\frac{-2}{3}=\frac{\left(-2\right).5}{3.5}=\frac{-10}{15}$.

Vì 9 < 10 nên –9 > –10 hay $\frac{-9}{15}>\frac{-10}{15}$ (hai phân số có cùng mẫu số dương)

Do đó, $\frac{-3}{5}>\frac{-2}{3}$ hay –0,6 > $\frac{-2}{3}$.

Luyện tập 4 trang 9 Toán lớp 7 Tập 1: So sánh:

a) – 3,23 và – 3,32;

b) $\frac{-7}{3}$ và – 1,25.

Lời giải:

a) Ta đi so sánh hai số đối của –3,23 và –3,32 lần lượt là 3,23 và 3,32.

Kể từ trái sang phải, cặp chữ số cùng hàng đầu tiên khác nhau là cặp chữ số hàng phần mười.

Vì 2 < 3 nên 3,23 < 3,32.

Do đó, –3,23 > –3,32.

b) Ta có: –1,25 = $\frac{-125}{100}=\frac{-5}{4}$ và $-\frac{7}{3}=\frac{-7}{3}$

Ta đi quy đồng mẫu số như sau:

$\frac{-5}{4}=\frac{\left(-5\right).3}{4.3}=\frac{-15}{12};\frac{-7}{3}=\frac{\left(-7\right).4}{3.4}=\frac{-28}{12}$.

Vì –15 > –28 nên $\frac{-15}{12}>\frac{-28}{12}$ .

Do đó $\frac{-5}{4}>\frac{-7}{3}$ hay –1,25 > $-\frac{7}{3}$.

Vậy –1,25 > $-\frac{7}{3}$.

Hoạt động 5 trang 9 Toán lớp 7 Tập 1: Giả sử hai điểm a, b lần lượt biểu diễn hai số nguyên a, b trên trục số nằm ngang. Với a < b, nêu nhận xét về vị trí của điểm a so với điểm b trên trục số đó.

Lời giải:

Vì a < b nên điểm a nằm bên trái của điểm b.

Bài tập

Giải Toán 7 trang 10 Tập 1

Bài 1 trang 10 Toán lớp 7 Tập 1: Các số 13; − 29; − 2,1; 2,28; $\frac{-12}{-18}$ có là số hữu tỉ không? Vì sao?

Lời giải:

• Ta có $13=\frac{13}{1}$ nên 13 viết được dưới dạng $\frac{a}{b}$, với a, b ∈ ℤ và b ≠ 0.

Do đó, 13 là số hữu tỉ;

• Ta có $-29=\frac{-29}{1}$ nên –29 viết được dưới dạng $\frac{a}{b}$, với a, b ∈ ℤ và b ≠ 0.

Do đó, –29 là số hữu tỉ;

• Ta có $-2,1=\frac{-21}{10}$ nên –2,1 viết được dưới dạng $\frac{a}{b}$, với a, b ∈ ℤ và b ≠ 0.

Do đó, –2,1 là số hữu tỉ;

• Ta có $2,28=\frac{228}{100}$ nên 2,28 viết được dưới dạng $\frac{a}{b}$, với a, b ∈ ℤ và b ≠ 0.

Do đó, 2,28 là số hữu tỉ;

• Ta có $\frac{-12}{-18}$ viết dưới dạng $\frac{a}{b}$, với a, b ∈ ℤ và b ≠ 0.

Do đó, $\frac{-12}{-18}$ là số hữu tỉ.

Bài 2 trang 10 Toán lớp 7 Tập 1: Chọn kí hiệu "∈", "∉" thích hợp cho $\boxed{?}$:

a) $21\boxed{?}\mathbb{Q}$;

b) $-7\boxed{?}\mathbb{N}$;

c) $\frac{5}{-7}\boxed{?}\mathbb{Z}$;

d) $0\boxed{?}\mathbb{Q}$;

e) $-\mathrm{7,3}\boxed{?}\mathbb{Q}$;

g) $3\frac{2}{9}\boxed{?}\mathbb{Q}$.

Lời giải:

a)

$21\boxed{\in }\mathbb{Q}$ do 21 = $\frac{21}{1}$ nên 21 là số hữu tỉ;

b)

$-7\boxed{\notin }\mathbb{N}$ do –7 là số nguyên âm nên –7 không thể thuộc tập số tự nhiên;

c)

$\frac{5}{-7}\boxed{\notin }\mathbb{Z}$ do $\frac{5}{-7}$ không phải là số nguyên;

d)

Vậy $0\boxed{\in }\mathbb{Q}$ do 0 = $\frac{0}{1}$ nên 0 là số hữu tỉ;

e)

$-7,3\boxed{\in }\mathbb{Q}$do –7,3 = $\frac{-73}{10}$ nên –7,3 là số hữu tỉ;

g)

$3\frac{2}{9}\boxed{\in }\mathbb{Q}$ do $3\frac{2}{9}=\frac{3.9+2}{9}=\frac{29}{9}$ nên $3\frac{2}{9}$ là số hữu tỉ.

Bài 3 trang 10 Toán lớp 7 Tập 1: Trong các phát biểu sau, phát biểu nào đúng, phát biểu nào sai?

a) Nếu a ∈ ℕ thì a ∈ ℚ

b) Nếu a ∈ ℤ thì a ∈ ℚ

c) Nếu a ∈ ℚ thì a ∈ ℕ

d) Nếu a ∈ ℚ thì a ∈ ℤ

e) Nếu a ∈ ℕ thì a ∉ ℚ

g) Nếu a ∈ ℤ thì a ∉ ℚ

Lời giải:

a) Phát biểu “Nếu a Î ℕ thì a Î ℚ” là đúng vì:

Mọi số tự nhiên a bất kỳ đều biểu diễn được dưới dạng phân số $\frac{a}{1}$.

Khi đó, nếu a là số tự nhiên thì a cũng là số hữu tỉ.

b) Phát biểu “Nếu a Î ℤ thì a Î ℚ” là đúng.

Mọi số nguyên a bất kỳ đều biểu diễn được dưới dạng phân số $\frac{a}{1}$.

Khi đó, nếu a là số nguyên thì a cũng là số hữu tỉ.

c) Phát biểu “Nếu a Î ℚ thì a Î ℕ” là sai.

Vì nếu a = 1 thuộc ℚ thì a thuộc vào ℕ.

Nhưng nếu a = –2 thuộc ℚ thì a không thuộc ℕ.

d) Phát biểu “Nếu a Î ℚ thì a Î ℤ” là sai.

Vì nếu a = $\frac{3}{4}$ thuộc ℚ thì a không thuộc ℤ.

e) Phát biểu “Nếu a Î ℕ thì a ∉ ℚ” là sai.

Vì mọi số tự nhiên đều là số hữu tỉ.

g) Phát biểu “Nếu a Î ℤ thì a ∉ ℚ” là sai.

Vì mọi số nguyên đều là số hữu tỉ.

Vậy các phát biểu đúng là: a, b và các phát biểu sai là: c, d, e, g.

Giải Toán 7 trang 11 Tập 1

Bài 4 trang 11 Toán lớp 7 Tập 1: Quan sát trục số sau và cho biết các điểm A, B, C, D biểu diễn những số nào:

Lời giải:

Ta thấy mỗi một đoạn thẳng đơn vị đều được chia thành 7 đoạn thẳng nhỏ bằng nhau nên một đoạn thẳng đơn vị mới bằng $\frac{1}{7}$ đơn vị cũ.

- Điểm A nằm bên trái số 0 và khoảng cách từ điểm A đến 0 là 9 đơn vị mới.

Do đó điểm A biểu diễn số $\frac{-9}{7}$.

- Điểm B nằm bên trái số 0 và khoảng cách từ điểm B đến 0 là 3 đơn vị mới.

Do đó điểm B biểu diễn số $\frac{-3}{7}$.

- Điểm C nằm bên phải số 0 và khoảng cách từ điểm C đến 0 là 2 đơn vị mới.

Do đó điểm C biểu diễn số $\frac{2}{7}$.

- Điểm D nằm bên phải số 0 và khoảng cách từ điểm D đến 0 là 6 đơn vị mới.

Do đó điểm D biểu diễn số $\frac{6}{7}$.

Vậy các điểm A, B, C, D lần lượt biểu diễn các số $\frac{-9}{7};\frac{-3}{7};\frac{2}{7};\frac{6}{7}$.

Bài 5 trang 11 Toán lớp 7 Tập 1: Tìm số đối của mỗi số sau: $\frac{9}{25};\frac{-8}{27};-\frac{15}{31};\frac{5}{-6};\mathrm{3,9};-\mathrm{12,5}$.

Lời giải:

Số đối của $\frac{9}{25}$ là $\frac{-9}{25}$ vì $\frac{9}{25}$ + $\left(-\frac{9}{25}\right)$ = 0

Số đối của $\frac{-8}{27}$ là $-\frac{-8}{27}=-\left(-\frac{8}{27}\right)=\frac{8}{27}$ vì $\frac{-8}{27}$+ $\frac{8}{27}=0$;

Số đối của $-\frac{15}{31}$ là $-\left(-\frac{15}{31}\right)=\frac{15}{31}$vì $\left(-\frac{15}{31}\right)$ + $\frac{15}{31}$ = 0;

Số đối của $\frac{5}{-6}$ là $-\frac{5}{-6}=-\left(-\frac{5}{6}\right)=\frac{5}{6}$vì $\frac{5}{-6}$ + $\frac{5}{6}$ = 0 ;

Số đối của 3,9 là −3,9 vì 3,9 + (–3,9) = 0.

Số đối của −12,5 là − (−12,5) = 12,5 vì (–12,5) + 12,5 = 0.

Bài 6 trang 11 Toán lớp 7 Tập 1: Biểu diễn số đối của mỗi số cho trên trục số sau:Lời giải:

Số đối của $\frac{-5}{6}$ là $-\frac{-5}{6}=\frac{5}{6}$;

Số đối của $\frac{-1}{3}$ là $-\frac{-1}{3}=\frac{1}{3}$;

Số đối của 0 là 0;

Số đối của 1 là − 1;

Số đối của $\frac{7}{6}$ là $-\frac{7}{6}$.

Các điểm A, B, O, C, D lần lượt biểu diễn các số $\frac{5}{6};\frac{1}{3};0;-1;-\frac{7}{6}$ trên trục số như hình vẽ sau:

Bài 7 trang 11 Toán lớp 7 Tập 1: So sánh:

a) 2,4 và $2\frac{3}{5}$;

b) − 0,12 và $-\frac{2}{5}$;

c) $\frac{-2}{7}$ và − 0,3.

Lời giải:

a) Ta có: $\mathrm{2,4}=\frac{24}{10}=\frac{24:2}{10:2}=\frac{12}{5}$;

$2\frac{3}{5}=2+\frac{3}{5}=\frac{10}{5}+\frac{3}{5}=\frac{13}{5}$.

Vì 12 < 13 nên $\frac{12}{5}<\frac{13}{5}$

Do đó $\mathrm{2,4}<2\frac{3}{5}$.

Vậy $\mathrm{2,4}<2\frac{3}{5}$.

b) Ta có $-0,12=\frac{-12}{100}=\frac{-12:4}{100:4}=\frac{-3}{25}$;

$-\frac{2}{5}=\frac{-2}{5}=\frac{-2.5}{5.5}=\frac{-10}{25}$.

Vì − 3 > − 10 nên $\frac{-3}{25}>\frac{-10}{25}$

Do đó $-\mathrm{0,12}>-\frac{2}{5}$.

Vậy $-\mathrm{0,12}>-\frac{2}{5}$.

c) Ta có $-\mathrm{0,3}=\frac{-3}{10}$.

Thực hiện quy đồng mẫu số hai phân số, ta được:

• $\frac{-2}{7}=\frac{-2.10}{7.10}=\frac{-20}{70}$

• $\frac{-3}{10}=\frac{-3.7}{10.7}=\frac{-21}{70}$.

Vì − 20 > − 21 nên $\frac{-20}{70}>\frac{-21}{70}$

Do đó $\frac{-2}{7}>-\mathrm{0,3}$.

Vậy $\frac{-2}{7}>-\mathrm{0,3}$.

Bài 8 trang 11 Toán lớp 7 Tập 1:

a) Sắp xếp các số sau theo thứ tự tăng dần: $\frac{-3}{7};\mathrm{0,4};-\mathrm{0,5};\frac{2}{7}$.

b) Sắp xếp các số sau theo thứ tự giảm dần: $\frac{-5}{6};-\mathrm{0,75};-\mathrm{4,5};-1$.

Lời giải:

a) Ta chia các số đã cho thành hai nhóm.

Nhóm 1 (gồm các số dương): 0,4 và $\frac{2}{7}.$

Nhớm 2 (gồm các số âm): –0,75 và $\frac{-5}{6}.$

• Ta đi so sánh nhóm 1:

Ta có: $0,4=\frac{4}{10}=\frac{4.7}{10.7}=\frac{28}{70}$ và $\frac{2}{7}=\frac{2.10}{7.10}=\frac{20}{70}$

Vì 28 > 20 nên $\frac{28}{70}>\frac{20}{70}$

Do đó 0,4 > $\frac{2}{7}$

• Ta đi so sánh nhóm 2:

Ta có: $-0,5=\frac{-5}{10}=\frac{\left(-5\right).7}{10.7}=\frac{-35}{70}$ và $\frac{-3}{7}=\frac{\left(-3\right).10}{7.10}=\frac{-30}{70}$.

Vì –30 > –35 nên $\frac{-35}{70}<\frac{-30}{70}$

Do đó $-0,5<\frac{-3}{7}$

Vì số âm luôn bé hơn số dương nên ta sắp xếp theo thứ tự tăng dần như sau:

$-0,5;\frac{-3}{7};\frac{2}{7};0,4$

b) Ta có $-0,75=\frac{-75}{100}=\frac{-3}{4}$; $-4,5=\frac{-45}{10}=\frac{-9}{2}$; $-1=\frac{-1}{1}$.

Thực hiện quy đồng mẫu số các phân số, ta được:

• $\frac{-5}{6}=\frac{\left(-5\right).2}{6.2}=\frac{-10}{12};$

• $\frac{-3}{4}=\frac{\left(-3\right).3}{4.3}=\frac{-9}{12};$

• $\frac{-9}{2}=\frac{\left(-9\right).6}{2.6}=\frac{-54}{12};$

• $\frac{-1}{1}=\frac{\left(-1\right).12}{1.12}=\frac{-12}{12}.$

Vì −9 > −10 > −12 > −54 nên $\frac{-9}{12}>\frac{-10}{12}>\frac{-12}{12}>\frac{-54}{12}$.

Hay $\frac{-3}{4}>\frac{-5}{6}>-1>\frac{-9}{2}$.

Do đó $-0,75>\frac{-5}{6}>-1>-4,5$.

Vậy các số được sắp xếp theo thứ tự giảm dần: $-0,75;\frac{-5}{6};-1;-4,5.$

Bài 9 trang 11 Toán lớp 7 Tập 1: Hình 4 mô tả một chiếc cân khối lượng, ở đó các vạch ghi 46 và 48 lần lượt ứng với các số đo 46 kg và 48 kg. Khi nhìn vị trí mà chiếc kim chỉ vào, bạn Minh đọc số đo là 47,15 kg, bạn Dương đọc số đo là 47,3 kg, bạn Quân đọc số đo là 47,65 kg. Bạn nào đã đọc đúng số đo? Vì sao?

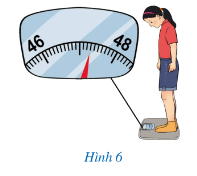
Lời giải:

Quan sát hình vẽ ta thấy:

• Từ vạch đậm chỉ số 46 đến vạch đậm chỉ số 48 lần lượt ứng với các số đo 46 kg và 48 kg.

Nên vạch đậm chính giữa hai vạch này chỉ số đo 47 kg.

• Từ vạch chỉ số đo 47 kg đến vạch chỉ số đo 48 kg được chia thành 10 đoạn nhỏ

Suy ra mỗi đoạn nhỏ này tương ứng với 0,1 kg.

Do đó từ vạch chỉ số 47 đến vị trí mà chiếc kim chỉ vào có 3 đoạn nhỏ ứng với 0,3 kg.

Khi đó chiếc kim chỉ 47,3 kg.

Vậy bạn Dương đã đọc đúng số đo.

Bài 10 trang 11 Toán lớp 7 Tập 1: Cô Hạnh dự định xây tầng hầm cho ngôi nhà của gia đình. Một công ty tư vấn xây dựng đã cung cấp cho cô Hạnh lựa chọn một trong sáu số đo chiều cao của tầng hầm như sau: 2,3 m; 2,35 m; 2,4 m; 2,55 m; 2,5 m; 2,75 m. Cô Hạnh dự định chọn chiều cao của tầng hầm lớn hơn $\frac{13}{5}$m để đảm bảo ánh sáng, thoáng đãng, cân đối về kiến trúc và thuận tiện trong sử dụng. Em hãy giúp cô Hạnh chọn đúng số đo chiều cao của tầng hầm.

Lời giải:

Ta có

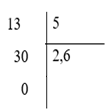
Do đó, $\frac{13}{5}=2,6$

Cô Hạnh dự định chọn chiều cao của tầng hầm lớn hơn $\frac{13}{5}$ m hay chiều cao lớn hơn 2,6 m.

Trong các số 2,3; 2,35; 2,4; 2,55; 2,5; 2,75 thì chỉ có 2,75 > 2,6

Do đó trong sáu lựa chọn mà công ty tư vấn xây dựng đã đưa ra cho cô Hạnh thì chỉ có chiều cao 2,75 m là thỏa mãn yêu cầu.

Vậy số đo chiều cao của tầng hầm cô Hạnh cần chọn là 2,75 m.

A. Lý thuyết Toán 7 Bài 1. Tập hợp ℚ các số hữu tỉ - Cánh diều

1. Số hữu tỉ

- Số hữu tỉ là số viết được dưới dạng phân số $\frac{a}{b}\left(a,b\in \mathbb{Z},b\ne 0\right)$ .

- Tập hợp các số hữu tỉ kí hiệu là ℚ.

Ví dụ: Các số $-7;\text{ 0,6; }-1,2;\text{ 1}\frac{4}{5}$ là các số hữu tỉ bởi vì chúng đều viết được dưới dạng phân số: $-7=\frac{-7}{1}\text{; 0,6=}\frac{6}{10};-\text{1,2=}\frac{-12}{10};\text{ 1}\frac{4}{5}=\frac{9}{5}$.

Chú ý:

- Mỗi số nguyên là một số hữu tỉ.

- Các phân số bằng nhau là cách viết khác nhau của cùng một số hữu tỉ.

Ví dụ: Vì $\frac{1}{2}=\frac{2}{4}$ nên $\frac{1}{2}$ và $\frac{2}{4}$cùng biểu diễn một số hữu tỉ.

2. Biểu diễn số hữu tỉ trên trục số

- Tương tự số nguyên ta có thể biểu diễn mọi số hữu tỉ trên trục số.

- Điểm biểu diễn số hữu tỉ a được gọi là điểm a.

- Do các phân số bằng nhau cùng biểu diễn một số hữu tỉ nên khi biểu diễn số hữu tỉ trên trục số ta chọn một trong những phân số đó để biểu diễn. Thông thường ta chọn phân số tối giản để biểu diễn số hữu tỉ đó.

- Nếu số hữu tỉ chưa viết dưới dạng phân số thì ta viết lại chúng dưới dạng phân số rồi biểu diễn phân số đó trên trục số.

Ví dụ: a) Biểu diễn số hữu tỉ 1,5 trên trục số.

- Ta viết 1,5 dưới dạng phân số: $1,5=\frac{15}{10}=\frac{3}{2}$. Ta sẽ biểu diễn phân số $\frac{3}{2}$ trên trục số.

- Chia đoạn thẳng đơn vị (chẳng hạn đoạn từ điểm 0 đến điểm 1) thành hai phần bằng nhau, lấy một đoạn làm đơn vị mới (đơn vị mới bằng $\frac{1}{2}$ đơn vị cũ).

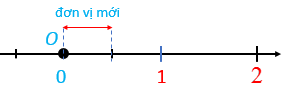
- Đi theo chiều dương của trục số bắt đầu từ điểm 0, ta lấy 3 đơn vị mới đến điểm M. Điểm M biểu diễn số hữu tỉ , và cũng chính là điểm biểu diễn số hữu tỉ 1,5 và $\frac{15}{10}$.

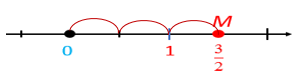b) Biểu diễn số hữu tỉ $\frac{-3}{2}$ trên trục số.

- Chia đoạn thẳng đơn vị (chẳng hạn đoạn từ điểm 0 đến điểm 1) thành hai phần bằng nhau, lấy một đoạn làm đơn vị mới (đơn vị mới bằng $\frac{1}{2}$ đơn vị cũ).

- Đi theo chiều ngược chiều dương của trục số bắt đầu từ điểm 0, ta lấy 3 đơn vị mới đến điểm N. Điểm N biểu diễn số hữu tỉ $\fr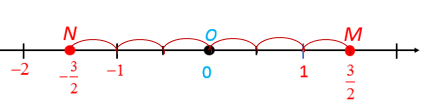ac{-3}{2}$.

Nhận xét: Vì $-\frac{3}{2}=\frac{-3}{2}=\frac{3}{-2}$ nên điểm N biểu diễn số $\frac{-3}{2}$ cũng là điểm biểu diễn số $\frac{-3}{2}$ và $\frac{3}{-2}$.

3. Số đối của một số hữu tỉ

- Trên trục số hai số hữu tỉ phân biệt có điểm biểu diễn nằm về hai phía của điểm gốc O và cách đều điểm gốc 0 được gọi là hai số đối nhau.

- Số đối của số hữu tỉ a, kí hiệu là –a.

- Số đối của số 0 là 0.

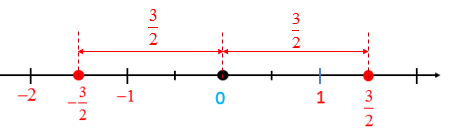Ví dụ:

- Số đối của số $\frac{3}{2}$ là số $-\frac{3}{2}$

- Số đối của số $\frac{-2}{7}$ là số $-\left(\frac{-2}{7}\right)=\frac{2}{7}$ .

4. So sánh các số hữu tỉ

4.1 So sánh hai số hữu tỉ

Trong hai số hữu tỉ khác nhau bao giờ cũng có một số nhỏ hơn số kia.

- Nếu số hữu tỉ a nhỏ hơn số hữu tỉ b thì ta viết a < b hay b > a

- Số hữu tỉ lớn hơn 0 gọi là số hữu tỉ dương.

- Số hữu tỉ nhỏ hơn 0 gọi là số hữu tỉ âm.

- Số hữu tỉ 0 không là số hữu tỉ âm cũng không là số hữu tỉ dương

- Nếu a < b và b < c thì a < c.

4.2 Cách so sánh hai số hữu tỉ

+ Khi hai số hữu tỉ cùng là phân số hoặc cùng là số thập phân, ta dùng quy tắc đã học ở lớp 6 để so sánh.

+ Các trường hợp khác hai trường hợp trên, để so sánh hai số hữu tỉ ta viết chúng cùng về dạng phân số (hoặc cùng dạng số thập phân) rồi so sánh chúng.

Ví dụ:

a) So sánh $-\frac{1}{3}$ và $\frac{-2}{5}$

Hai phân số trên cùng là phân số, vì vậy ta sẽ áp dụng quy tắc so sánh hai phân số đã học.

Ta quy đồng để đưa hai phân số về cùng mẫu số dương

$-\frac{1}{3}=\frac{-1}{3}=\frac{(-1)\cdot 5}{3\cdot 5}=\frac{-5}{15}$; $\frac{-2}{5}=\frac{(-2)\cdot 3}{5\cdot 3}=\frac{-6}{15}$

Vì $-5>-6$ nên $\frac{-5}{15}>\frac{-6}{15}$. Suy ra $-\frac{1}{3}>\frac{-2}{5}$.

b) So sánh 1,206 và 1,3

Hai số trên cùng là số thập phân, vì vậy ta sẽ áp dụng quy tắc so sánh hai số thập phân.

Ta so sánh phần nguyên với nhau, khi phần nguyên bằng nhau ta sẽ so sánh đến phần thập phân, lần lượt từ hàng phần mười, hàng phần trăm, hàng phần nghìn…

1,206 < 1,3 (vì phần nguyên bằng nhau, hàng phần mười có 2 < 3).

c) So sánh – 0,3 và $\frac{-2}{7}$

Ta thấy hai số trên chưa cùng là phân số hoặc số thập phân, vì vậy ta đưa chúng về cùng là phân số hoặc số thập phân sau đó so sánh chúng.

Ta có $-0,3=\frac{-3}{10}$, ta sẽ áp dụng quy tắc so sánh hai phân số $\frac{-3}{10}$và $\frac{-2}{7}$

Ta có : $\frac{-3}{10}=\frac{(-3)\cdot 7}{10\cdot 7}=\frac{-21}{70}$; $\frac{-2}{7}=\frac{(-2)\cdot 10}{7\cdot 10}=\frac{-20}{70}$

Vì – 21 < –20 nên $\frac{-21}{70}<\frac{-20}{70}$. Suy ra – 0,3 < $\frac{-2}{7}$ .

4.3 Minh họa trên trục số

Hai điểm x, y lần lượt biểu diễn hai số hữu tỉ x, y trên trục số :

- Trên trục số nằm ngang: Nếu x < y hay y > x thì điểm x nằm bên trái điểm y.

- Trên trục số thẳng đứng: Nếu x < y hay y > x thì điểm x nằm phía dưới điểm y.

Ví dụ : So sánh hai số: – 2 và $\frac{-5}{3}$

Ta có : $-2=\frac{-2}{1}=\frac{-6}{3}$ mà $\frac{-6}{3}<\frac{-5}{3}$ vậy nên $-2<\frac{-5}{3}$ .

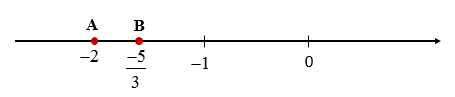Trên trục số nằm ngang điểm – 2 nằm bên trái điểm $\frac{-5}{3}$.

Xem thêm lời giải bài tập Toán lớp 7 Cánh diều hay, chi tiết khác:

Bài 2: Cộng, trừ, nhân, chia số hữu tỉ

Bài 3: Phép tính lũy thừa với số mũ tự nhiên của một số hữu tỉ

Bài 4: Thứ tự thực hiện các phép tính. Quy tắc dấu ngoặc

Bài 5: Biểu diễn thập phân của số hữu tỉ

Bài tập ôn tập chương 1