Lý thuyết Xác suất của biến cố (mới 2023 + Bài Tập) – Toán 11

Lý thuyết Toán 11 Bài 5: Xác suất của biến cố

Bài giảng Toán 11 Bài 5: Xác suất của biến cố

A. Lý thuyết

I. Định nghĩa cổ điển của xác suất.

Giả sử A là biến cố liên quan đến một phép thử với không gian mẫu chỉ có một số hữu hạn kết quả đồng khả năng xuất hiện. Ta gọi tỉ số $\frac{n\left(A\right)}{n\left(\Omega \right)}$ là xác suất của biến cố A, kí hiệu là P(A).  Vậy  P(A) = $\frac{n\left(A\right)}{n\left(\Omega \right)}$.

- Chú ý: n(A) là số phần tử của A hay cũng là số các kết quả thuận lợi cho biến cố A, còn $n\left(\Omega \right)$ là số các kết quả có thể xảy ra của phép thử.

- Ví dụ 1. Gieo con súc sắc cân đối và đồng chất liên tiếp hai lần. Biến cố A: “Lần đầu xuất hiện mặt 3 chấm”.  Tính n(A), P(A).

Lời giải:

Gieo con súc sắc liên tiếp 2 lần, khi đó: .

Các kết quả thuận lợi cho A là:

A = {(3; 1); (3; 2); (3; 3); (3; 4); (3; 5); (3; 6)}.

Do đó; n(A) = 6.

Khi đó xác suất để xảy ra biến cố A là $P\left(A\right)=\frac{n\left(A\right)}{n\left(\Omega \right)}=\frac{6}{36}=\frac{1}{6}$.

- Ví dụ 2. Gieo một đồng tiền liên tiếp ba lần. Gọi B là biến cố: lần gieo thứ nhất và thứ hai giống nhau. Tính n(B), P(B)?

Lời giải:

Gieo một đồng tiền liên tiếp ba lần, khi đó: $n\left(\Omega \right)=2^3=8.$

Các kết quả thuận lợi cho biến cố B là:

B = {SSS; SSN; NNN; NNS}.

Do đó; n(B) = 4.

Vậy xác suất để xảy ra biến cố B là $P\left(B\right)=\frac{n\left(B\right)}{n\left(\Omega \right)}=\frac{4}{8}=\frac{1}{2}$.

II. Tính chất của xác suất

Giả sử A và B là các biến cố liên quan đến một phép thử có một số hữu hạn kết quả đồng khả năng xuất hiện. Khi đó, ta có định lí sau:

a) $P(\varnothing )=\text{\hspace{0.17em}\hspace{0.17em}}0;P\left(\Omega \right)=1$.

b) 0 ≤ P(A) ≤ 1 , với mọi biến cố A.

c) Nếu A và B xung khắc thì:

$P(A\cup B)=P\left(A\right)+P\left(B\right)$ (công thức cộng xác suất )

- Hệ quả: Với mọi biến cố A, ta có: $P\left(\overline{A}\right)=1-P\left(A\right)$.

- Ví dụ 3. Gieo đồng tiền 5 lần cân đối và đồng chất. Xác suất để được ít nhất một lần xuất hiện mặt sấp là:

Lời giải:

Phép thử : Gieo đồng tiền 5 lần cân đối và đồng chất

Ta có : $n\left(\Omega \right)=2^5=32$.

Biến cố A: Được ít nhất một lần xuất hiện mặt sấp.

Biến cố đối $\overline{A}$ tất cả đều là mặt ngửa.

Chỉ có duy nhất một trường hợp tất cả các mặt đều ngửa nên $n\left(\overline{A}\right)=1$

Suy ra: $n\left(A\right)=n\left(\Omega \right)-n\left(\overline{A}\right)=31$

Xác suất của biến cố A là $P\left(A\right)=\frac{n\left(A\right)}{n\left(\Omega \right)}=\frac{31}{32}$.

- Ví dụ 4. Một bình đựng 5 viên bi xanh và 3 viên bi đỏ (các viên bi chỉ khác nhau về màu sắc). Lấy ngẫu nhiên một viên bi, rồi lấy ngẫu nhiên một viên bi nữa. Tính xác suất của biến cố “lấy lần thứ hai được một viên bi xanh”.

Lời giải:

Gọi A là biến cố “lấy lần thứ hai được một viên bi xanh”. Có hai trường hợp xảy ra

- Biến cố B: Lấy lần thứ nhất được bi xanh, lấy lần thứ hai cũng được một bi xanh.

Xác suất trong trường hợp này là  $P_B=\frac{5}{8}.\frac{4}{7}=\frac{5}{14}$

- Biến cố C: Lấy lần thứ nhất được bi đỏ, lấy lần thứ hai được bi xanh.

Xác suất trong trường hợp này là $P_C=\frac{3}{8}.\frac{5}{7}=\frac{15}{56}$

- Vì 2 biến cố B và C là xung khắc nên P_A = P_B + P_C = 0,625.

III. Các biến cố độc lập, công thức nhân xác suất.

- Nếu sự xảy ra của một biến cố không ảnh hưởng đến xác suất xảy ra của một biến cố khác thì ta nói hai biến cố đó độc lập.

- Tổng quát:

 A và B là hai biến cố độc lập khi và chỉ khi: P(A.B) = P(A).P(B).

- Ví dụ 5. Ba người cùng bắn vào 1 bia. Xác suất để người thứ nhất, thứ hai,thứ ba bắn trúng  đích lần lượt là 0,8 ; 0,6; 0,6. Xác suất để có đúng 2 người bắn trúng đích bằng:

Lời giải:

Gọi X là biến cố: “có đúng 2 người bắn trúng đích”.

- Gọi A là biến cố: “người thứ nhất bắn trúng đích”, $P\left(A\right)=0,8;P\left(\overline{A}\right)=0,2$

- Gọi B là biến cố: “người thứ hai bắn trúng đích”, $P\left(B\right)=0,6;P\left(\overline{B}\right)=0,4$.

- Gọi C là biến cố: “người thứ ba bắn trúng đích”, $P\left(C\right)=0,6;P\left(\overline{C}\right)=0,4$

Ta thấy biến cố A, B, C là 3 biến cố độc lập nhau, theo công thức nhân xác suất ta có:

$$\begin{gathered} P\left(X\right)=P\left(A.B.\overline{C}\right)+P(A.\overline{B}.C)+ \\ P(\overline{A}.B.C) \end{gathered}$$

= 0,8.0,6.0.4 + 0,8.0,4.0,6 + 0,2.0,6.0,6 = 0,456.

B. Bài tập tự luyện

Bài 1. Một hộp đựng 11 tấm thẻ được đánh số từ 1 đến 11. Chọn ngẫu nhiên 6 tấm thẻ. Tính xác suất để tổng số ghi trên 6 tấm thẻ ấy là một số lẻ?

Lời giải:

 Số phần tử của không gian mẫu là $n\left(\Omega \right)=C_{11}^6=462$.

Gọi biến cố A: “tổng số ghi trên 6 tấm thẻ ấy là một số lẻ”.

Từ 1 đến 11 có 6 số lẻ và 5 số chẵn.

Để có tổng là một số lẻ ta có 3 trường hợp.

-Trường hợp 1: Chọn được 1 thẻ mang số lẻ và 5 thẻ mang số chẵn có:

$6.C_5^5=6$ cách.

-Trường hợp 2: Chọn được 3 thẻ mang số lẻ và 3 thẻ mang số chẵn có:

$C_6^3.C_5^3=200$ cách.

-Trường hợp 3: Chọn được 5 thẻ mang số lẻ và 1 thẻ mang số chẵn có:

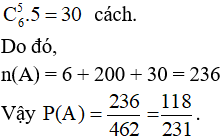
Bài 2. Một bình đựng 4 quả cầu xanh và 6 quả cầu trắng.

a) Chọn ngẫu nhiên 3 quả cầu. Tính xác suất để được 3 quả cầu toàn màu xanh.

b) Chọn ngẫu nhiên 4 quả cầu. Tính xác suất để được 2 quả cầu xanh và 2 quả cầu trắng.

Lời giải:

a) Phép thử : Chọn ngẫu nhiên ba quả cầu.

Ta có: $n\left(\Omega \right)=C_{10}^3=120$.

Biến cố A : Được ba quả toàn màu xanh.

$\Rightarrow n\left(A\right)=C_4^3=4$

 Xác suất để được 3 quả cầu toàn màu xanh là $P\left(A\right)=\frac{n\left(A\right)}{n\left(\Omega \right)}=\frac{1}{30}$.

b)

Phép thử : Chọn ngẫu nhiên bốn quả cầu.

Ta có $n\left(\Omega \right)=C_{10}^4=210$.

Biến cố B: Được hai quả xanh, hai quả trắng

$\Rightarrow n\left(B\right)=C_4^2.C_6^2=90$

 Xác suất để được 2 quả cầu xanh và 2 quả cầu trắng

$P\left(B\right)=\frac{n\left(B\right)}{n\left(\Omega \right)}=\frac{3}{7}$

Bài 3. Một đội gồm 5 nam và 8 nữ. Lập một nhóm gồm 4 người đi biểu diễn văn nghệ. Tính xác suất để trong 4 người được chọn có ít nhất 3 nữ.

Lời giải:

Không gian mẫu là chọn tùy ý 4 người từ 13 người.

Suy ra số phần tử của không gian mẫu là $n\left(\Omega \right)=C_{13}^4=715$

Gọi A là biến cố “4 người được chọn có ít nhất 3 nữ”.

Ta có hai trường hợp thuận lợi cho biến cố A như sau:

- TH1: Chọn 3 nữ và 1 nam, có $C_8^3.C_5^1=280$ cách.

Bài 4. Một hộp có 5 viên bi xanh, 6 viên bi đỏ và 7 viên bi vàng. Chọn ngẫu nhiên 5 viên bi trong hộp. Tính xác suất để 5 viên bi được chọn có đủ màu và số bi đỏ bằng số bi vàng.

Lời giải:

Hộp bi có tất cả: 5 + 6 + 7 = 18 viên bi.

Không gian mẫu là số cách chọn ngẫu nhiên 5 viên bi từ hộp chứa 18 viên bi.

Suy ra số phần tử của không gian mẫu là $n\left(\Omega \right)=C_{18}^5=8568$.

Gọi A là biến cố “5 viên bi được chọn có đủ màu và số bi đỏ bằng số bi vàng’.

Ta có các trường hợp thuận lợi cho biến cố A là:

- TH1: Chọn 1 bi đỏ, 1 bi vàng và 3 bi xanh nên có $C_6^1.C_7^1.C_5^3=420$ cách.

- TH2: Chọn 2 bi đỏ, 2 bi vàng và 1 bi xanh nên có $C_6^2.C_7^2.C_5^1=1575$ cách.

Suy ra số phần tử của biến cố A là n(A) = 420 + 1575 = 1995.

Vậy xác suất cần tính $P\left(A\right)=\frac{1995}{8568}=\frac{95}{408}$.

Trắc nghiệm Toán 11 Bài 5: Xác suất của biến cố

Câu 1: Cho A là một biến cố liên quan phép thử T. Mệnh đề nào sau đây là mệnh đề đúng ?

A. $P\left(A\right)$ là số lớn hơn 0.

B. $P\left(A\right)=1-P\left(\overline{A}\right)$.

C. $P\left(A\right)=0\iff A=\Omega$.

D. $P\left(A\right)$ là số nhỏ hơn 1.

Hiển thị đáp án  

Đáp án: D

Giải thích:

Loại trừ :A ;B ;C đều sai

Câu 2: Gieo đồng tiền hai lần. Xác suất để sau hai lần gieo thì mặt sấp xuất hiện ít nhất một lần

A. $\frac{1}{4}$

B. $\frac{1}{2}$

C. $\frac{3}{4}$

D. $\frac{1}{3}$

Hiển thị đáp án  

Đáp án: C

Giải thích:

Số phần tử không gian mẫu: $n\left(\Omega \right)=2.2=4$

Biến cố xuất hiện mặt sấp ít nhất một lần: $A=\left\{SN;NS;SS\right\}$

Suy ra $P\left(A\right)=\frac{n\left(A\right)}{n\left(\Omega \right)}=\frac{3}{4}$.

Câu 3: Gieo đồng tiền 5 lần cân đối và đồng chất. Xác suất để được ít nhất một lần xuất hiện mặt sấp là:

A. $\frac{31}{32}$

B. $\frac{21}{32}$

C. $\frac{11}{32}$

D. $\frac{1}{32}$

Hiển thị đáp án  

Đáp án: A

Giải thích:

Phép thử : Gieo đồng tiền 5 lần cân đối và đồng chất

Ta có  $n\left(\Omega \right)=2^5=32$ 

Biến cố A : Được ít nhất một lần xuất hiện mặt sấp

$\overline{A}$ : Tất cả đều là mặt ngửa

$n\left(\overline{A}\right)=1$

$\Rightarrow n\left(A\right)=n\left(\Omega \right)-n\left(\overline{A}\right)=31$

$\Rightarrow p\left(A\right)=\frac{n\left(A\right)}{n\left(\Omega \right)}=\frac{31}{32}$

Câu 4: Gieo đồng tiền 5 lần cân đối và đồng chất. Xác suất để được ít nhất một đồng tiền xuất hiện mặt sấp là

A. $\frac{31}{32}$

B. $\frac{21}{32}$

C. $\frac{11}{32}$

D. $\frac{1}{32}$

Hiển thị đáp án  

Đáp án: A

Giải thích:

$n\left(\Omega \right)=2^5=32$.

A : “được ít nhất một đồng tiền xuất hiện mặt sấp”.

Xét biến cố đối $\overline{A}$ : “không có đồng tiền nào xuất hiện mặt sấp”.

$\overline{A}=\left\{\left(N,N,N,N,N\right)\right\}$, có $n\left(\overline{A}\right)=1$.

Suy ra $n\left(A\right)=32-1=31$.

KL: $P\left(A\right)=\frac{n\left(A\right)}{n\left(\Omega \right)}=\frac{31}{32}$.

Câu 5: Gieo ngẫu nhiên một đồng tiền cân đối và đồng chất bốn lần. Xác suất để cả bốn lần gieo đều xuất hiện mặt sấp là:

A. $\frac{4}{16}$

B. $\frac{2}{16}$

C. $\frac{1}{16}$

D. $\frac{6}{16}$

Hiển thị đáp án  

Đáp án: C

Giải thích:

Gọi A là biến cố: “cả bốn lần gieo đều xuất hiện mặt sấp.”

-Không gian mẫu: $2^4=16.$

- $n\left(A\right)=\mathrm{1.1.1.1}=1.$

=> $P\left(A\right)=\frac{n\left(A\right)}{\left|\Omega \right|}=\frac{1}{16}.$

Câu 6: Một con súc sắc đồng chất được đổ 6 lần. Xác suất để được một số lớn hơn hay bằng 5 xuất hiện ít nhất 5 lần là

A.  $\frac{31}{23328}$

B.  $\frac{41}{23328}$

C.  $\frac{51}{23328}$

D  $\frac{21}{23328}$

Hiển thị đáp án  

Đáp án: B

Giải thích:

Ta có  $n\left(\Omega \right)=\mathrm{6.6.6.6.6.6}=6^6.$

Có các trường hợp sau:

1. Số bằng 5 xuất hiện đúng 5 lần

$\Rightarrow$ có 30 kết quả thuận lợi.

2. Số bằng 5 xuất hiện đúng 6 lần

$\Rightarrow$ có 1 kết quả thuận lợi.

3. Số bằng 6 xuất hiện đúng 5 lần

$\Rightarrow$ có 30 kết quả thuận lợi.

4. Số bằng 6 xuất hiện đúng 6 lần

$\Rightarrow$ có 1 kết quả thuận lợi.

Vậy xác suất để được một số lớn hơn hay bằng 5 xuất hiện ít nhất 5 lần là

$P=\frac{30+1+30+1}{6^6}=\frac{31}{23328}.$

Câu 7: Gieo ngẫu nhiên hai con súc sắc cân đối, đồng chất. Xác suất của biến cố “Tổng số chấm của hai con súc sắc bằng 6” là

A.  $\frac{5}{6}$

B.   $\frac{7}{36}$

C.   $\frac{11}{36}$

D.   $\frac{5}{36}$

Hiển thị đáp án  

Đáp án: D

Giải thích:

Gọi A là biến cố: “Tổng số chấm của hai con súc sắc bằng 6.”

-Không gian mẫu: $6^2=36.$

-Ta có  

$$\begin{gathered} 1+5=6,2+4=6,3+3=6, \\ 4+2=6,5+1=6. \end{gathered}$$

=> $n\left(A\right)=5.$

=> $P\left(A\right)=\frac{n\left(A\right)}{\left|\Omega \right|}=\frac{5}{36}.$

Câu 8: Gieo hai con súc sắc. Xác suất để tổng số chấm trên hai mặt chia hết cho 3 là:

A. $\frac{13}{36}$

B. $\frac{11}{36}$

C. $\frac{1}{3}$

D. $\frac{1}{16}$

Hiển thị đáp án  

Đáp án: C

Giải thích:

Số phần tử không gian mẫu: $n\left(\Omega \right)=6.6=36$

Biến cố tổng hai mặt chia hết cho 3 là:

$A=\left\{\begin{array}{l}\left(1;2\right);\left(1;5\right);\left(2;1\right);\left(2;4\right);\\ \left(3;3\right);\left(3;6\right);\left(4;2\right);\left(4;5\right);\\ \left(5;1\right);\left(5;4\right);\left(6;3\right);\left(6;6\right)\end{array}\right\}$

nên $n\left(A\right)=12$.

Suy ra $P\left(A\right)=\frac{n\left(A\right)}{n\left(\Omega \right)}=\frac{12}{36}=\frac{1}{3}$.

Câu 9: Gieo ba con súc sắc. Xác suất để nhiều nhất hai mặt 5 là:

A. $\frac{5}{72}$

B.  $\frac{1}{216}$

C. $\frac{1}{72}$

D. $\frac{215}{216}$

Hiển thị đáp án  

Đáp án: D

Giải thích:

Số phần tử không gian mẫu: $n\left(\Omega \right)=\mathrm{6.6.6}=216$

Biến cố có ba mặt 5 là: $\overline{A}=\left\{\left(5;5;5\right)\right\}$ nên $n\left(\overline{A}\right)=1$.

Suy ra

$P\left(A\right)=1-P\left(\overline{A}\right)=1-\frac{n\left(\overline{A}\right)}{n\left(\Omega \right)}=\frac{215}{216}$.

Câu 10: Gieo một con súc sắc 3 lần. Xác suất để được mặt số hai xuất hiện cả 3 lần là:

A. $\frac{1}{172}$

B. $\frac{1}{18}$

C. $\frac{1}{20}$

D. $\frac{1}{216}$

Hiển thị đáp án  

Đáp án: D

Giải thích:

Số phần tử không gian mẫu: $n\left(\Omega \right)=\mathrm{6.6.6}=216$

Số phần tử của biến cố xuất hiện mặt số hai ba lần: $n\left(A\right)=1$

Suy ra $P\left(A\right)=\frac{n\left(A\right)}{n\left(\Omega \right)}=\frac{1}{216}$.

Xem thêm các bài tổng hợp lý thuyết Toán lớp 11 đầy đủ, chi tiết khác:

Lý thuyết Ôn tập chương 2

Lý thuyết Phương pháp quy nạp toán học 

Lý thuyết Dãy số

Lý thuyết Cấp số cộng

Lý thuyết Cấp số nhân