Lý thuyết Phương pháp quy nạp toán học (mới 2024 + Bài Tập)

Lý thuyết Toán 11 Bài 1: Phương pháp quy nạp toán học

Bài giảng Toán 11 Bài 1: Phương pháp quy nạp toán học

A. Lý thuyết

I. Phương pháp quy nạp toán học

Để chứng minh những mệnh đề liên quan đến số tự nhiên là đúng với mọi n mà không thể thử trực tiếp được thì có thể làm như sau:

- Bước 1. Kiểm tra mệnh đề đúng với n = 1.

- Bước 2. Giả thiết mệnh đề đúng với một số tự nhiên bất kì n = k ≥ 1 (gọi là giả thiết quy nạp), chứng minh rằng nó cũng đúng với n = k + 1.

Đó là phương pháp quy nạp toán học, hay còn gọi tắt là phương pháp quy nạp.

II. Ví dụ áp dụng

- Ví dụ 1. Chứng minh với mọi số tự nhiên n ≥ 1 ta có:

$1+2+3+\mathrm{...}+\text{\hspace{0.17em}}n=\frac{n(n+\text{\hspace{0.17em}}1)}{2}$ (*)

Lời giải:

Bước 1: Với n = 1 ta có:

Vế trái = 1 và vế phải = 1

Vậy hệ thức đúng với n = 1.

Bước 2: Giả sử hệ thức đúng với một số tự nhiên bất kì n = k ≥ 1 tức là:

$1+2+3+\mathrm{...}+\text{\hspace{0.17em}}k$$=\frac{k(k+\text{\hspace{0.17em}}1)}{2}$ (1)

Ta cần chứng minh hệ thức đúng với n = k + 1, tức là:

$1+2+3+\mathrm{...}+\text{\hspace{0.17em}}k+k+\text{}1$$=\frac{(k+\text{}1)(k+2)}{2}$ (2)

Thật vậy:

Vế trái = 1 + 2 + 3+ … + k + k + 1

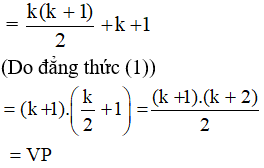
Vậy hệ thức đã cho đúng với mọi số tự nhiên n ≥ 1.

- Ví dụ 2. Chứng minh rằng với , ta có bất đẳng thức

$\frac{\mathrm{1.3.5....}(2n-1)}{\mathrm{2.4.6.}..2n}<\frac{1}{\sqrt{2n+1}}$

Lời giải:

- Với n = 1, bất đẳng thức cho trở thành: $\frac{1}{2}<\frac{1}{\sqrt{3}}$ (đúng).

Vậy bất đẳng thức cho đúng với n = 1.

- Giả sử bất đẳng thức cho đúng với mọi số tự nhiên n = k ≥ 1, tức là :

$\frac{\mathrm{1.3.5....}(2k-1)}{\mathrm{2.4.6.}..2k}$$<\frac{1}{\sqrt{2k+1}}$ (1)

-Ta chứng minh bất đẳng thức cho đúng với n = k + 1, tức là :

$\frac{\mathrm{1.3.5....}(2k-1)(2k+\text{}1)}{\mathrm{2.4.6.}..2k(2k+\text{\hspace{0.17em}}2)}$$\hspace{0.17em}\hspace{0.17em}<\frac{1}{\sqrt{2k+3}}$ (2)

Thật vậy, ta có :

$VT\left(2\right)=\frac{\mathrm{1.3.5....}(2k-1)}{\mathrm{2.4.6.}..2k}.$$\frac{2k+\text{}1}{2k+\text{}2}<\frac{1}{\sqrt{2k+1}}.$$\frac{2k+\text{}1}{2k+\text{}2}=\frac{\sqrt{2k+\text{\hspace{0.17em}}1}}{2k+\text{}2}$ (theo (1))

Ta chứng minh:

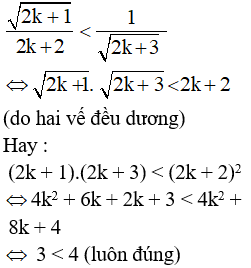
Vậy bất đẳng thức đã cho đúng với mọi số tự nhiên n ≥ 1.

- Chú ý:

Nếu phải chứng minh mệnh đề là đúng với mọi số tự nhiên n ≥ p (p là một số tự nhiên) thì:

+ Ở bước 1, ta phải kiểm tra mệnh đề đúng với n = p;

+ Ở bước 2, ta giả thiết mệnh đề đúng với số tự nhiên bất kì n = k ≥ p và phải chứng minh rằng nó cũng đúng với n = k + 1.

B. Bài tập tự luyện

Bài 1. Với mỗi số nguyên dương n, chứng minh:

$$\begin{gathered} 1^2+\text{\hspace{0.17em}}{2}^2+3^2+\text{\hspace{0.17em}}\mathrm{...}+\text{\hspace{0.17em}}{n}^2= \\ \frac{n(n+\text{\hspace{0.17em}\hspace{0.17em}}1).(2n+\text{\hspace{0.17em}}1)}{6} \end{gathered}$$

Lời giải:

- Với n = 1 thì vế trái = 1² = 1 và vế phải = $\frac{1(1+1)(2.1+1)}{6}=1$.

Vậy đẳng thức đúng với n = 1.

- Giả sử đẳng thức đúng với n = k ≥ 1, tức là:

$$\begin{gathered} 1^2+\text{\hspace{0.17em}}{2}^2+3^2+\text{\hspace{0.17em}}\mathrm{...}+\text{\hspace{0.17em}}{k}^2 \\ =\frac{k(k+\text{\hspace{0.17em}\hspace{0.17em}}1).(2k+\text{\hspace{0.17em}}1)}{6} \end{gathered}$$

- Ta chứng minh đẳng thức cũng đúng với n = k + 1, tức là chứng minh

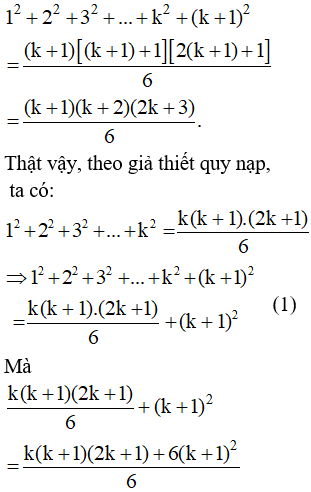
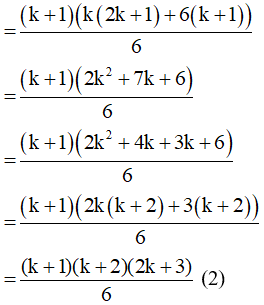
Từ (1); (2) suy ra

$1^2+2^2+3^2+\mathrm{...}+k^2+{(k+1)}^2$$=\frac{(k+1)(k+2)(2k+3)}{6}.$

Do đó đẳng thức đúng với n = k + 1. Suy ra có điều phải chứng minh.

Bài 2. Chứng minh rằng với mọi số tự nhiên n ≥ 4, ta có: 2^{n + 1} > n² + 3n.

Lời giải:

Bước 1: Với n = 4 thì vế trái bằng 2^{4 + 1} = 32 và vế phải bằng 4² + 3.4 = 28 .

Do 32 > 28 nên bất đẳng thức đúng với n = 4.

Bước 2: Giả sử đẳng thức đúng với n = k ≥ 4, nghĩa là 2^{k + 1} > k² + 3k.

Ta chứng minh bất đẳng thức cũng đúng với n = k + 1, tức là phải chứng minh

2^{(k + 1) + 1} > (k + 1)² + 3(k + 1) hay 2^{k + 2} > k² + 5k + 4

Thật vậy, theo giả thiết quy nạp ta có 2^{k + 1} > k² + 3k.

Suy ra, 2.2^{k + 1} > 2.(k² + 3k) hay 2^{k + 2} > 2k² + 6k.

Mặt khác: 2k² + 6k – (k² + 5k + 4) = k² + k – 4 ≥ 4² + 4 – 3 = 16 với mọi k ≥ 4.

Do đó, 2^{k + 2} > 2k² + 6k > k² + 5k + 4 hay bất đẳng thức đúng với n = k + 1.

Suy ra bất đẳng thức được chứng minh.

Bài 3. Bằng phương pháp quy nạp toán học, chứng minh rằng 7ⁿ + 5 chia hết cho 6 với n ≥ 1.

Lời giải:

Thật vậy: Với n = 1 thì 7¹ + 5 = 12 ⁝ 6.

Giả sử mệnh đề đúng với n = k ≥ 1, nghĩa là 7^k + 5 chia hết cho 6.

Ta chứng minh mệnh đề đúng với n = k + 1, nghĩa là phaỉ chứng minh 7^{k + 1} + 5 chia hết cho 6.

Ta có: 7^{k + 1} + 5 = 7(7^k + 5) – 30.

Theo giả thiết quy nạp thì (7^k + 5) ⁝ 6 nên 7(7^k + 5) ⁝ 6

Lại có: 30 ⁝ 6 nên (7^{k + 1} + 5) ⁝ 6

Vậy 7ⁿ + 5 chia hết cho 6 với mọi n ≥ 1 .

Trắc nghiệm Toán 11 Bài 1: Phương pháp quy nạp toán học

Câu 1. Với mọi số tự nhiên n , tổng $S_n=n^3+3n^2+5n+3$ chia hết cho:

A. 3

B. 4

C. 5

D. 7

Hiển thị đáp án

Đáp án: A

Giải thích:

Với n = 0 ta có: $S_0=3$ chia hết cho 3, ta chứng minh $S_n=n^3+3n^2+5n+3$ chia hết cho 3 với mọi số tự nhiên n.

Giả sử mệnh đề trên đúng đến $n=k$ , tức là $S_k=k^3+3k^2+5k+3$ chia hết cho 3, ta chứng minh mệnh đề trên đúng đến $n=k+1$, tức là $S_{k+\text{}1}$ cũng chia hết cho 3.

Ta có:

$S_{k+1}$

$={(k+1)}^3+3{(k+1)}^2+5(k+1)+3$

$\begin{array}{l}=k^3+6k^2+14k+12\end{array}$

$\begin{array}{l}=(k^3+3k^2+5k+3)\\ +3(k^2+3k+3)\end{array}$

Có: $S_k=k^3+3k^2+5k+3$ chia hết cho 3 theo giả thiết quy nạp, $3(k^2+3k+3)⋮3$, do đó $S_{k+1}⋮3$

Vậy $S_n⋮3$ với mọi số tự nhiên n.

Câu 2. Giá trị của tổng là:

$S=1-2+3-4+\mathrm{...}-2n+(2n+1)$

A. 1

B. 0

C. 5

D. n +1

Hiển thị đáp án

Đáp án: D

Giải thích:

Với =0 ta có: $S=1$

Với =1 ta có $S$ =1–2+3=2

Với =2 ta có $S$=1–2+3–4+5=3

Dự đoán S = n+1$\left(*\right)$ ta sẽ chứng minh $\left(*\right)$đúng bằng quy nạp.

Với n = 0 đương nhiên $\left(*\right)$ đúng.

Giả sử $\left(*\right)$ đúng với $n=k$, tức là

$S_k=1-2+3-4+\mathrm{...}-2k+(2k+1)$

$=k+1$, ta chứng minh $\left(*\right)$ đúng với $n=k$ +1.

Ta có:

$S_{k+1}=1-2+3-4+\mathrm{...2}(k-1)$

$+\left(2\right(k+1)+1)$

$=(1-2+3-4+\mathrm{...}-2k+2k+1)$

$-(2k+2)+(2k+3)$

$=S_k-(2k+2)+(2k+3)$

$=k+1-2k-2+\text{}2k+3$

$=k+\text{}2$

Vậy $\left(*\right)$ đúng với mọi số tự nhiên n, tức là S = n+1.

Câu 3. Với mọi số nguyên dương n , tổng $S_n=1.2+2.3+3.4+\mathrm{...}+n(n+1)$ là:

A. $\frac{n(n+1)(n+2)(n+3)}{6}$

B. $\frac{n(n+1)(n+2)}{3}$

C. $\frac{n(n+1)(n+2)}{2}$

D. Đáp số khác

Hiển thị đáp án

Đáp án: B

Giải thích:

Với =1 ta có: S =1.2=2, do đó đáp án A, C sai.

Ta chứng minh $S_n=\frac{n(n+1)(n+2)}{3}(*)$ đúng với mọi số nguyên dương .

Giả sử $\left(*\right)$ đúng đến , tức là

$S_k=1.2+2.3+3.4+\mathrm{...}+k(k+1)$

$=\frac{k(k+1)(k+2)}{3}$

, ta chứng minh (∗) đúng đến $n=k+1$, tức là cần chứng minh

$S_{k+1}$

$=1.2+2.3+\mathrm{...}+(k+1)(k+2)$

$=\frac{(k+1)(k+2)(k+3)}{3}$

Ta có:

$\begin{array}{l}{S}_{k+1}=1.2+2.3+\mathrm{...}+k(k+1)\\ +(k+1)(k+2)\\ =\frac{k(k+1)(k+2)}{3}+(k+1)(k+2)\\ =(\text{}k\text{}+1).\left(\frac{k^2+\text{}2k}{3}+\text{}k+2\right)\\ =\frac{(k+1)(k^2+2k+3k+6)}{3}\\ =\frac{(k+1)(k^2+5k+6)}{3}\\ =\frac{(k+1)(k+2)(k+3)}{3}\end{array}$

Vậy $\left(*\right)$ đúng với mọi số nguyên dương n.

Câu 4: Một học sinh chứng minh mệnh đề $\text{'}\text{'}{8}^n+1$ chia hết cho $7,\forall n\in N^{*}\text{'}\text{'}(*)$ như sau:

Giả sử $\left(*\right)$ đúng với $n=k$ tức là $8^k$+ 1 chia hết cho 7

Ta có: $8^k$+ 1 = 8$(8^k+1)$- 7, kết hợp với giả thiết $8^k$+ 1 chia hết cho 7 nên suy ra được $8^{k+1}$+ 1 chia hết cho 7.

Vậy đẳng thức $\left(*\right)$ đúng với mọi $n\in N^{*}$

Khẳng định nào sau đây là đúng?

A. Học sinh trên chứng minh đúng.

B. Học sinh chứng minh sai vì không có giả thiết qui nạp.

C. Học sinh chứng minh sai vì không dùng giả thiết qui nạp.

D. Học sinh không kiểm tra bước 1 (bước cơ sở) của phương pháp qui nạp

Hiển thị đáp án

Đáp án: D

Giải thích:

Quan sát lời giải trên ta thấy:

Học sinh thực hiện thiếu bước 1: Kiểm tra $n=1$ thì $8^1$+1=9 không chia hết cho 7 nên mệnh đề đó sai.

Câu 5: Với $n\in N^{*}$ , ta xét các mệnh đề: $P$ :“ $7^n$ + 5 chia hết cho 2”;

Q: “$7^n$+ 5 chia hết cho 3” và R: “$7^n$+ 5 chia hết cho 6”.

Số mệnh đề đúng trong các mệnh đề trên là:

A. 3

B. 0

C. 1

D. 2

Hiển thị đáp án

Đáp án: A

Giải thích:

Bằng quy nạp toán học ta chứng minh được $7^n$ + 5 chia hết cho 6.

Thật vậy, với n = 1 ta có: $7^1$ + 5 =12 $⋮$ 6

Giả sử mệnh đề đúng với n = k , nghĩa là $7^k$ + 5 chia hết cho 6, ta chứng minh mệnh đề cũng đúng với , nghĩa là phải chứng minh $7^{k+1}$ + 5 chia hết cho 6.

Ta có: $7^{k+1}$ + 5 =7($7^k$+5)−30

Theo giả thiết quy nạp ta có $7^k$+5chia hết cho 6, và 30 chia hết cho 6 nên

7($7^k$+5)−30cũng chia hết cho 6.

Do đó mệnh đề đúng với $n=k+1$.

Vậy $7^n$ + 5 chi hết cho 6 với mọi $n\in N^{*}$

Mọi số chia hết cho 6 đều chia hết cho 2 và chia hết cho 3.

Do đó cả 3 mệnh đề đều đúng.

Câu 6: Trong phương pháp quy nạp toán học, nếu ta giả sử mệnh đề đúng với $n=k$ thì ta cần chứng minh mệnh đề đúng đến:

A. $n=k-1$

B. $n=k-2$

C. $n=k+1$

D. $n=k+2$

Hiển thị đáp án

Đáp án: C

Giải thích:

Nếu ta giả sử mệnh đề đúng với $n=k$ thì ta cần chứng minh mệnh đề đúng với $n=k+1$

Câu 7: Đối với bài toán chứng minh $P\left(n\right)$ đúng với mọi $n\ge p$ với p là số tự nhiên cho trước thì ở bước 1 ta cần chứng minh mệnh đề đúng với:

A. $n=1$

B. $n=k$

C. $n=k+1$

D. $n=p$

Hiển thị đáp án

Đáp án: D

Giải thích:

Đối với bài toán chứng minh $P\left(n\right)$ đúng với mọi $n\ge p$ với p là số tự nhiên cho trước thì:

- Bước 1: Chứng minh $P\left(n\right)$ đúng với $n=p$

- Bước 2: Với $k\ge p$ là một số nguyên dương tùy ý, giả sử $P\left(n\right)$ đúng với $n=k$, chứng minh $P\left(n\right)$ cũng đúng khi $n=k+1$.

Từ đó ta thấy, ở bước đầu tiên ta cần chứng minh mệnh đề đúng với $n=p$ chứ không phải $n=1$.

Câu 8: Dùng quy nạp chứng minh mệnh đề chứa biến $P\left(n\right)$ đúng với mọi số tự nhiên $n\ge p$ (p là một số tự nhiên). Ở bước 2 ta giả thiết mệnh đề $P\left(n\right)$ đúng với $n=k$. Khẳng định nào sau đây là đúng?

A. $k\ne p$

B. $k\ge p$

C. $k=p$

D. $k<p$

Hiển thị đáp án

Đáp án: B

Giải thích:

Ở bước 2 ta cần giả sử mệnh đề đúng với $n=k$ với $k\ge p$.

Câu 9: Khi sử dụng phương pháp quy nạp để chứng minh mệnh đề chứa biến đúng với mọi số tự nhiên $n\ge p$ ( p là một số tự nhiên), ta tiến hành hai bước:

- Bước 1, kiểm tra mệnh đề $P\left(n\right)$ đúng với $n=p$

- Bước 2, giả thiết mệnh đề $P\left(n\right)$ đúng với số tự nhiên bất kỳ $n=k\ge p$ và phải chứng minh rằng nó cũng đúng với $n=k+1$

Trong hai bước trên:

A. Chỉ có bước 1 đúng.

B. Chỉ có bước 2 đúng.

C. Cả hai bước đều đúng

D. Cả hai bước đều sai

Hiển thị đáp án

Đáp án: C

Giải thích:

Đối với bài toán chứng minh $P\left(n\right)$ đúng với mọi $n\ge p$ với p là số tự nhiên cho trước thì:

- Bước 1: Chứng minh $P\left(n\right)$ đúng với $n=p$.

- Bước 2: Với là một số nguyên dương tùy ý, giả sử đúng với , chứng minh cũng đúng khi $n=k+1$.

Từ lý thuyết trên ta thấy cả hai bước trên đều đúng.

Câu 10: Trong phương pháp quy nạp toán học, ở bước 2, nếu ta giả sử mệnh đề đúng với $n=k+1$ thì ta cần chứng minh mệnh đề đúng với:

A. $n=k$

B. $n=k+1$

C. $n=k+2$

D. $n=k+3$

Hiển thị đáp án

Đáp án: B

Giải thích:

Phương pháp quy nạp toán học:

- Bước 1: Chứng minh $P\left(n\right)$ đúng với $n=1$.

- Bước 2: Với k là một số nguyên dương tùy ý, giả sử $P\left(n\right)$ đúng với $n=k$, chứng minh $P\left(n\right)$ cũng đúng khi $n=k+1$.

Do đó ta thấy, ở bước 2, nếu ta giả sử mệnh đề đúng với thì ta cần chứng minh mệnh đề đúng với 1

Xem thêm các bài tổng hợp lý thuyết Toán lớp 11 đầy đủ, chi tiết khác:

Lý thuyết Dãy số

Lý thuyết Cấp số cộng

Lý thuyết Cấp số nhân

Lý thuyết Ôn tập chương 3

Lý thuyết Giới hạn của dãy số