Lý thuyết Ôn tập chương 2 (mới 2023 + Bài Tập)– Toán 11

Lý thuyết Toán 11 Ôn tập chương 2

A. Lý thuyết

1. Quy tắc cộng

- Quy tắc cộng: Một công việc được hoàn thành bởi một trong hai hành động. Nếu hành động này có m cách thực hiện, hành động kia có n cách thực hiện không trùng với bất kì cách nào của hành động thứ nhất thì công việc đó có m + n cách thực hiện.

- Quy tắc cộng được phát biểu ở trên thực chất là quy tắc đếm số phần tử của hợp hai tập hợp hữu hạn không giao nhau, được phát biểu như sau:

Nếu A và B là các tập hợp hữu hạn và không giao nhau thì:

$n(A\cup B)=n\left(A\right)+n\left(B\right)$

- Chú ý: Quy tắc cộng có thể mở rộng cho nhiều hành động.

- Ví dụ 1. Một lớp học có 21 bạn nữ và 19 bạn nam. Giáo viên chủ nhiệm cần chọn một bạn để làm lớp trưởng. Hỏi giáo viên có bao nhiêu cách chọn?

Lời giải:

+ Trường hợp 1. Giáo viên chọn 1 bạn nam: có 19 cách.

+ Trường hợp 2. Giáo viên chọn 1 bạn  nữ: có 21 cách

Theo quy tắc cộng, giáo viên sẽ có: 19 + 21 = 40 cách chọn 1 bạn làm lớp trưởng.

- Ví dụ 2. Bạn Lan có 10 quyển sách khác nhau; 12 chiếc bút khác nhau và 5 cục tẩy khác nhau. Bạn Lan cần chọn một món đồ để đem tặng Hoa. Hỏi bạn Lan có bao nhiêu cách chọn?

Lời giải:

Bạn Lan có thể chọn:

+ Một quyển sách: có 10 cách chọn

+ Một chiếc bút: có 12 cách chọn.

+ Một cục tẩy: có 5 cách chọn.

Theo quy tắc cộng, bạn Lan có: 10 + 12 + 5 =  27 cách chọn.

2. Quy tắc nhân

- Quy tắc nhân: Một công việc được hoàn thành bởi hai hành động liên tiếp. Nếu có m cách thực hiện hành động thứ nhất và ứng với mỗi cách đó có n cách thực hiện hành động thứ hai thì có m.n cách hoàn thành công việc.

- Chú ý: Quy tắc nhân có thể mở rộng cho nhiều hành động liên liếp.

- Ví dụ 3. Cho tập A = {1; 3; 4; 5; 6}. Hỏi lập được bao nhiêu số tự nhiên có 2 chữ số đôi một khác nhau từ tập A?

Lời giải:

Để tạo ra một số tự nhiên có 2 chữ số đôi một khác nhau từ tập A, ta phải thực hiện liên tiếp hai hành động:

- Hành động 1: Chọn chữ số hàng chục có 5 cách.

- Hành động 2. Chọn chữ số hàng đơn vị. Ứng với mỗi cách chọn chữ số hàng chục, ta có 4 cách chọn chữ số hàng đơn vị (vì chữ số hàng chục khác chữ số hàng đơn vị).

Theo quy tắc nhân, số các số tự nhiên thỏa mãn đầu bài là: 5.4 = 20 số.

- Ví dụ 4. Một người vào cửa hàng ăn, người đó chọn thực đơn gồm 1 món ăn trong 10 món, 1 loại quả tráng miệng trong 6 loại quả tráng miệng và 1 nước uống giải khát trong 4 loại nước uống. Hỏi có bao nhiêu cách chọn thực đơn?

Lời giải:

Để chọn một thực đơn, ta cần thực hiện liên tiếp ba hành động:

- Chọn 1 món ăn trong 10 món có 10 cách.

- Chọn 1 loại quả tráng miệng trong 6 loại quả tráng miệng có 6 cách.

- Chọn 1 nước uống trong 4 loại nước uống có 4 cách.

Theo quy tắc nhân, số cách cách chọn thực đơn là 10.6.4 = 240 cách.

3. Hoán vị

3.1 Định nghĩa

- Định nghĩa: Cho tập hợp A gồm n phần tử (n ≥ 1). Mỗi kết quả của sự sắp xếp thứ tự n phần tử của tập hợp A được gọi là một hoán vị của n phần tử đó.

- Nhận xét: Hai hoán vị của n phần tử khác nhau ở thứ tự sắp xếp.

Chẳng hạn, hai hoán vị abc và cab của ba phần tử a; b; c là khác nhau.

3.2 Số các hoán vị

Kí hiệu: P_n là số các hoán vị của n phần tử.

- Định lí: P_n = n.(n – 1).(n – 2)….2.1

- Chú ý: Kí hiệu n.(n – 1)…2.1 là n! (đọc là n là giai thừa), ta có: P_n = n!.

- Ví dụ 1. Có bao nhiêu cách xếp 10 học sinh thành một hàng ngang.

Lời giải:

Số cách xếp 10 học sinh thành một hàng ngang là 10! cách.

4. Chỉnh hợp

4.1 Định nghĩa.

- Cho tập hợp A gồm n phần tử (n ≥ 1).

Kết quả của việc lấy k phần tử khác nhau từ n phần tử của tập hợp A và sắp xếp chúng theo một thứ tự nào đó được gọi là một chỉnh hợp chập k của n phần tử đã cho.

- Ví dụ 2. Lớp 11A2 có 40 học sinh. Khi đó; mỗi cách chọn ra 4 bạn làm tổ trưởng tổ 1; tổ 2; tổ 3; tổ 4 chính là số chỉnh hợp chập 4 của 40 học sinh.

4.2 Số các chỉnh hợp

- Kí hiệu $A_n^k$ là số các chỉnh hợp chập k của n phần tử (1 ≤ k ≤ n) .

- Định lí:

$A_n^k=n(n-1)\mathrm{...}(n-k+\text{\hspace{0.17em}}1)$

- Ví dụ 3. Từ năm điểm phần biệt A; B; C; D; E  ta lập được bao nhiêu vectơ khác $\overrightarrow{0}$ có điểm đầu và điểm cuối là năm điểm đã cho.

Lời giải:

Một vectơ được xác định khi biết điểm đầu và điểm cuối của nó.

Số vecto khác $\overrightarrow{0}$ có điểm đầu và điểm cuối là năm điểm đã cho chính là chỉnh hợp chập 2 của 5 phần tử:

Do đó, ta có: $A_5^2=\mathrm{5.4.3}=60$ vectơ thỏa mãn đầu bài.

- Chú ý:

a) Với quy ước 0! = 1 ta có: $A_n^k=\frac{n!}{(n-k)!};$$\hspace{0.17em}1\le k\le n$.

b) Mỗi hoán vị của n phần tử cũng chính là một chỉnh hợp chập n của n phần tử đó.

Vì vậy: $P_n=\text{\hspace{0.17em}\hspace{0.17em}}{A}_n^n$.

5. Tổ hợp

5.1 Định nghĩa.

- Giả sử tập A có n phần tử (n ≥ 1). Mỗi tập con gồm k phần tử của A được gọi là một tổ hợp chập k của n phần tử đã cho.

- Chú ý: Số k trong định nghĩa cần thỏa mãn điều kiện 1 ≤ k ≤ n. Tuy vậy, tập hợp không có phần tử nào là tập rỗng nên ta quy ước gọi tổ hợp chập 0 của n phần tử là tập rỗng.

- Ví dụ 4. Cho tập A = {3; 4; 5; 6}.

Ta liệt kê các tổ hợp chập 3 của A là: {3; 4; 5}; {3; 4; 6}; {3; 5; 6}; {4; 5; 6}.

5.2 Số các tổ hợp.

Kí hiệu $C_n^k$ là số các tổ hợp chập k của n phần tử ( 0 ≤ k ≤ n).

- Định lí: $C_n^k=\frac{n!}{k!(n-k)!}$.

Ví dụ 5. Cho 8 điểm phân biệt A; B; C; D; E; F; G; H, trong đó không có 3 điểm nào thẳng hàng, ta lập được bao nhiêu tam giác có 3 đỉnh là 8 điểm đã cho.

Lời giải:

Mỗi tam giác được lập là 1 tổ hợp chập 3 của 8 (điểm).

Vì vậy số tam giác có 3 đỉnh là 8 điểm đã cho là $C_8^3=$56.

5.3 Tính chất của các số $C_n^k$

a) Tính chất 1.

$C_n^k=C_n^{n-k};0\le k\le n$

Ví dụ 7. $C_8^4+C_8^5=C_9^5=126$.

6. Công thức nhị thức Niu- tơn

Ta có:

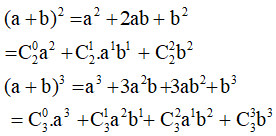
- Công thức nhị thức Niu – tơn.

$$\begin{gathered} {(a\text{\hspace{0.17em}\hspace{0.17em}}+b)}^n=C_n^0{a}^n+\text{\hspace{0.17em}\hspace{0.17em}}{C}_n^1.a^{n-1}b \\ +\text{\hspace{0.17em}}\mathrm{...}+\text{\hspace{0.17em}\hspace{0.17em}}{C}_n^k.a^{n-k}{b}^k\text{\hspace{0.17em}}+\text{}\mathrm{....}+ \\ \text{}{C}_n^{n-1}a{b}^{n-1}+\text{\hspace{0.17em}\hspace{0.17em}}{C}_n^n{b}^n \end{gathered}$$

- Hệ quả:

Với a = b = 1 ta có: $2^n=C_n^0+\text{\hspace{0.17em}}{C}_n^1+\text{}\mathrm{...}\text{}+\text{\hspace{0.17em}}{C}_n^n$

Với a = 1; b = – 1 ta có: $0=C_n^0-\text{\hspace{0.17em}}{C}_n^1+\text{}\mathrm{...}$$+\text{}{(-1)}^k.C_n^k+\text{}\mathrm{...}\text{}+{(-1)}^n\text{\hspace{0.17em}}{C}_n^n$

- Chú ý:

Trong biểu thức ở vế phải của công thức (1):

a) Số các hạng tử là n + 1.

b) Các hạng tử có số mũ của a giảm dần từ n đến 0; số mũ của b tăng dần từ 0 đến n, nhưng tổng các số mũ của a và b trong mỗi hạng tử luôn bằng n (quy ước $a^0=b^0=1$).

c) Các hệ số của mỗi cặp hạng tử cách đều hai hạng tử đầu và cuối thì bằng nhau.

- Ví dụ 1. Khai triển biểu thức: (a – b)⁵.

Lời giải:

Áp dụng công thức nhị thức Niu – tơn ta có:

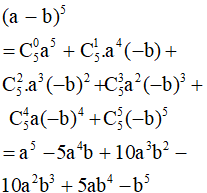
- Ví dụ 2. Khai triển biểu thức: (3x – 2)⁴.

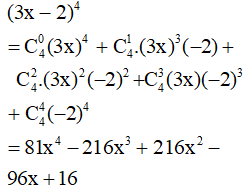
7. Tam giác Pa- xcan

Trong công thức nhị thức Niu – tơn ở mục I, cho n = 0; 1; … và xếp các hệ số thành dòng, ta nhận được tam giác sau đây, gọi là tam giác Pa- xcan.

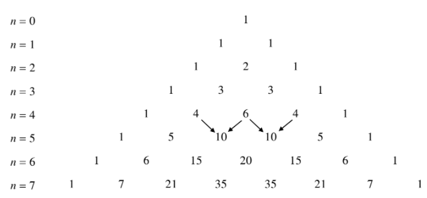
- Nhận xét:

Từ công thức $C_n^k=C_{n-1}^{k-1}+C_{n-1}^k$ suy ra cách tính các số ở mỗi dòng dựa vào các số ở dòng trước nó.

Ví dụ 3. $C_6^2=C_5^1+C_5^2$$=5+10=15$.

8. Phép thử, không gian mẫu

8.1 Phép thử.

Một trong những khái niệm cơ bản của lí thuyết xác suất là phép thử. Một thí nghiệm, một phép đo, hay một sự quan sát hiện tượng nào đó… được hiểu là phép thử.

- Ví dụ 1. Gieo ba đồng tiền xu liên tiếp, chọn ba cây tú lơ khơ từ bộ bài 52 cây tứ lơ khơ, chọn 3 bông hoa từ 10 bông hoa trong lọ… đây đều là phép thử.

- Khi gieo một đồng tiền, ta không thể đoán trước được mặt xuất hiện là sấp hay ngửa. Đó là ví dụ về phép thử ngẫu nhiên.

- Tổng quát. Phép thử ngẫu nhiên là phép thử mà ta không đoán trước được kết quả của nó, mặc dù đã biết tập hợp tất cả các kết quả có thể có của phép thử đó.

8.2 Không gian mẫu.

Tập hợp các kết quả có thể xảy ra của một phép thử được gọi là không gian mẫu của phép thử và kí hiệu là $\Omega$ (đọc là ô-mê-ga).

- Ví dụ 2. Nếu phép thử là gieo một con súc sắc một lần, thì không gian mẫu gồm 6 phần tử là: $\Omega$ = {1; 2; 3; 4; 5; 6}.

- Ví dụ 3. Nếu phép thử là gieo một đồng tiền ba lần thì không gian mẫu gồm tám phần tử là:

{SSS; SSN; SNS; SNN; NSS; NSN; NNS; NNN} .

9. Biến cố.

- Một cách tổng quát, mỗi biến cố liên quan đến một phép thử được mô tả bởi một tập con của không gian mẫu.

- Định nghĩa: Biến cố là một tập con của không gian mẫu.

Ta thường kí hiệu các biến cố bằng các chữ in hoa A; B; C…

- Tập $\varnothing$ được gọi là biến cố không thể (gọi tắt là biến cố không). Còn tập  được gọi là biến cố chắc chắn.

- Ví dụ 4. Gieo con súc sắc liên tiếp hai lần thì biến cố: “lần thứ nhất ra mặt 5 chấm, lần thứ 2 ra mặt 8 chấm” là biến cố không. (vì súc sắc không có mặt 8 chấm)

Còn biến cố: “Tổng số chấm hai lần gieo lớn hơn 1 và nhỏ hơn 13” là biến cố chắc chắn.

- Ta nói rằng biến cố A xảy ra trong một phép thử nào đó khi và chỉ khi các kết quả của phép thử đó là một phần tử của A (hay thuận lợi cho A).

Như vậy, biến cố không thể không bao giờ xảy ra. Trong khi đó, biến cố chắc chắn luôn luôn xảy ra.

10. Phép toán trên các biến cố.

Giả sử A là biến cố liên quan đến một phép thử

- Tập $\Omega$\A được gọi là biến cố đối của biến cố A, kí hiệu là $\overline{A}$.

$\overline{A}$ xảy ra khi và chỉ khi A không xảy ra.

- Ví dụ 5. Nếu phép thử là chọn một học sinh trong lớp làm lớp trường thì:

Biến cố A: “bạn đó là nữ”.

Biến cố B: “bạn đó là nam”.

Ta thấy, B là biến cố đối của biến cố A: $B=\overline{A}$.

 - Giả sử A và B là hai biến cố liên quan đến một phép thử. Ta có định nghĩa:

Tập $A\cup B$ được gọi là hợp của các biến cố A và B.

Tập $A\cap B$ được gọi là giao của các biến cố A và B.

Nếu $A\cap B=\varnothing$ thì ta còn nói A và B xung khắc.

- Biến cố $A\cup B$ xảy ra khi và chỉ khi A xảy ra hoặc B xảy ra.

Biến cố $A\cap B$ xảy ra khi và chỉ khi A và B đồng thời xảy ra.

Biến cố $A\cap B$ còn được viết là A.B.

A và B xung khắc khi và chỉ khi chúng không khi nào cùng xảy ra.            

- Ta có bảng sau:

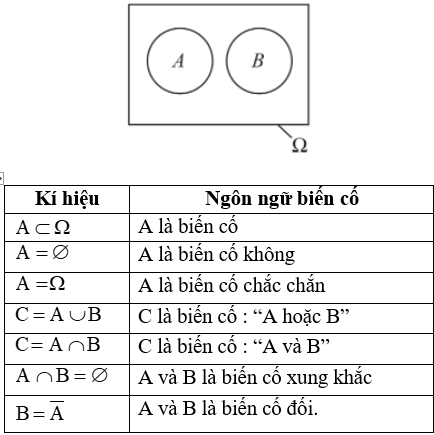
- Ví dụ 6. Xét phép thử: gieo súc sắc hai lần liên tiếp, với các biến cố:

A: “Kết quả hai lần gieo giống nhau”.

B. “Lần đầu xuất hiện mặt 5 chấm”.

Liệt kê các kết quả thuận lợi cho các biến A và B.

Lời giải:

A = {(1; 1); (2; 2); (3; 3); (4; 4); (5; 5); (6; 6)}.

B = {(5; 1); (5; 2); (5; 3); (5; 4); (5; 5); (5; 6)}.

11. Định nghĩa cổ điển của xác suất.

Giả sử A là biến cố liên quan đến một phép thử với không gian mẫu chỉ có một số hữu hạn kết quả đồng khả năng xuất hiện. Ta gọi tỉ số $\frac{n\left(A\right)}{n\left(\Omega \right)}$ là xác suất của biến cố A, kí hiệu là P(A).  Vậy  P(A) = $\frac{n\left(A\right)}{n\left(\Omega \right)}$.

- Chú ý: n(A) là số phần tử của A hay cũng là số các kết quả thuận lợi cho biến cố A, còn $n\left(\Omega \right)$ là số các kết quả có thể xảy ra của phép thử.

- Ví dụ 1. Gieo con súc sắc cân đối và đồng chất liên tiếp hai lần. Biến cố A: “Lần đầu xuất hiện mặt 3 chấm”.  Tính n(A), P(A).

Lời giải:

Gieo con súc sắc liên tiếp 2 lần, khi đó: .

Các kết quả thuận lợi cho A là:

A = {(3; 1); (3; 2); (3; 3); (3; 4); (3; 5); (3; 6)}.

Do đó; n(A) = 6.

Khi đó xác suất để xảy ra biến cố A là $P\left(A\right)=\frac{n\left(A\right)}{n\left(\Omega \right)}=\frac{6}{36}=\frac{1}{6}$.

- Ví dụ 2. Gieo một đồng tiền liên tiếp ba lần. Gọi B là biến cố: lần gieo thứ nhất và thứ hai giống nhau. Tính n(B), P(B)?

Lời giải:

Gieo một đồng tiền liên tiếp ba lần, khi đó: $n\left(\Omega \right)=2^3=8.$

Các kết quả thuận lợi cho biến cố B là:

B = {SSS; SSN; NNN; NNS}.

Do đó; n(B) = 4.

Vậy xác suất để xảy ra biến cố B là $P\left(B\right)=\frac{n\left(B\right)}{n\left(\Omega \right)}=\frac{4}{8}=\frac{1}{2}$.

12. Tính chất của xác suất

Giả sử A và B là các biến cố liên quan đến một phép thử có một số hữu hạn kết quả đồng khả năng xuất hiện. Khi đó, ta có định lí sau:

a) $P(\varnothing )=\text{\hspace{0.17em}\hspace{0.17em}}0;P\left(\Omega \right)=1$.

b) 0 ≤ P(A) ≤ 1 , với mọi biến cố A.

c) Nếu A và B xung khắc thì:

$P(A\cup B)$$\hspace{0.17em}=P\left(A\right)+P\left(B\right)$ (công thức cộng xác suất )

- Hệ quả: Với mọi biến cố A, ta có: $P\left(\overline{A}\right)=1-P\left(A\right)$.

- Ví dụ 3. Gieo đồng tiền 5 lần cân đối và đồng chất. Xác suất để được ít nhất một lần xuất hiện mặt sấp là:

Lời giải:

Phép thử : Gieo đồng tiền 5 lần cân đối và đồng chất

Ta có : $n\left(\Omega \right)=2^5=32$.

Biến cố A: Được ít nhất một lần xuất hiện mặt sấp.

Biến cố đối $\overline{A}$ tất cả đều là mặt ngửa.

Chỉ có duy nhất một trường hợp tất cả các mặt đều ngửa nên $n\left(\overline{A}\right)=1$

Suy ra: $n\left(A\right)=n\left(\Omega \right)-n\left(\overline{A}\right)=31$

Xác suất của biến cố A là $P\left(A\right)=\frac{n\left(A\right)}{n\left(\Omega \right)}=\frac{31}{32}$.

- Ví dụ 4. Một bình đựng 5 viên bi xanh và 3 viên bi đỏ (các viên bi chỉ khác nhau về màu sắc). Lấy ngẫu nhiên một viên bi, rồi lấy ngẫu nhiên một viên bi nữa. Tính xác suất của biến cố “lấy lần thứ hai được một viên bi xanh”.

Lời giải:

Gọi A là biến cố “lấy lần thứ hai được một viên bi xanh”. Có hai trường hợp xảy ra

- Biến cố B: Lấy lần thứ nhất được bi xanh, lấy lần thứ hai cũng được một bi xanh.

Xác suất trong trường hợp này là  $P_B=\frac{5}{8}.\frac{4}{7}=\frac{5}{14}$

- Biến cố C: Lấy lần thứ nhất được bi đỏ, lấy lần thứ hai được bi xanh.

Xác suất trong trường hợp này là $P_C=\frac{3}{8}.\frac{5}{7}=\frac{15}{56}$

- Vì 2 biến cố B và C là xung khắc nên P_A = P_B + P_C = 0,625.

13. Các biến cố độc lập, công thức nhân xác suất.

- Nếu sự xảy ra của một biến cố không ảnh hưởng đến xác suất xảy ra của một biến cố khác thì ta nói hai biến cố đó độc lập.

- Tổng quát:

 A và B là hai biến cố độc lập khi và chỉ khi: P(A.B) = P(A).P(B).

- Ví dụ 5. Ba người cùng bắn vào 1 bia. Xác suất để người thứ nhất, thứ hai,thứ ba bắn trúng  đích lần lượt là 0,8 ; 0,6; 0,6. Xác suất để có đúng 2 người bắn trúng đích bằng:

Lời giải:

Gọi X là biến cố: “có đúng 2 người bắn trúng đích”.

- Gọi A là biến cố: “người thứ nhất bắn trúng đích”, $P\left(A\right)=0,8;P\left(\overline{A}\right)=0,2$

- Gọi B là biến cố: “người thứ hai bắn trúng đích”, $P\left(B\right)=0,6;P\left(\overline{B}\right)=0,4$.

- Gọi C là biến cố: “người thứ ba bắn trúng đích”, $P\left(C\right)=0,6;P\left(\overline{C}\right)=0,4$

Ta thấy biến cố A, B, C là 3 biến cố độc lập nhau, theo công thức nhân xác suất ta có:

$$\begin{gathered} P\left(X\right)=P\left(A.B.\overline{C}\right)+P(A.\overline{B}.C)+ \\ P(\overline{A}.B.C) \end{gathered}$$

= 0,8.0,6.0.4 + 0,8.0,4.0,6 + 0,2.0,6.0,6 = 0,456.

B. Bài tập tự luyện

Bài 1. Lớp 11A có 43 học sinh, trong đó có 11 học sinh giỏi nữ, 7 học sinh giỏi nam. Giáo viên chủ nhiệm cần chọn hai học sinh giỏi của lớp gồm 1 nam và 1 nữ để tham gia đại hội chi đoàn. Hỏi giáo viên có bao nhiêu cách lựa chọn ?

Lời giải:

Để lựa chọn được hai bạn thỏa mãn yêu cầu, ta chia làm hai công việc liên liếp:

Công việc 1: Chọn một học sinh giỏi nữ, có 11 cách thực hiện.

Công việc 2: Chọn một học sinh giỏi nam, có 7 cách thực hiện.

Vậy theo quy tắc nhân, sẽ có 11.7 = 77 cách lựa chọn.

Bài 2. Trên bàn có 5 viên bi xanh được đánh số từ 1 đến 5; 4 viên bi đỏ được đánh số từ 1 đến 4; 2 viên bi vàng được đánh số từ 1 đến 2.

a) Hỏi có bao nhiêu cách lấy ra 1 viên bi?

b) Hỏi có bao nhiêu cách lấy ra ba viên bi khác màu ?

Lời giải:

a) Để chọn 1 viên bi ta có các trường hợp sau:

- Chọn 1 viên bi xanh có 5 cách.

- Chọn 1 viên bi đỏ có 4 cách.

- Chọn 1 viên bi vàng có 2 cách.

Theo quy tắc cộng có 5 + 4 + 2 = 11 cách lấy ra một bi.

b) Để lấy ra ba viên bi khác màu ta có 3 hành động liên tiếp cần thực hiện:

Bước 1: Chọn 1 viên bi xanh bất kì: có 5 cách thực hiện.

Bước 2: Chọn 1 viên bi đỏ bất kì: có 4 cách thực hiện.

Bước 3: Chọn 1 viên bi vàng bất kì: có 2 cách thực hiện.

Vậy theo quy tắc nhân có: 5.4. 2 = 40 cách chọn.

Bài 3. Một căn phòng được trang bị 6 bóng đèn. Để phòng có ánh sáng cần ít nhất một bóng đèn phải được bật. Hỏi có bao nhiêu cách bật, tắt các bóng đèn để căn phòng có ánh sáng ?

Lời giải:

Với mỗi bóng đèn ta có hai sự lựa chọn trạng thái là bật hoặc tắt.

Như vậy, theo quy tắc nhân sẽ có 2⁶ = 64 cách lựa chọn bật, tắt các bóng đèn đó.

Tuy nhiên có một trạng thái duy nhất là khi cả 6 bóng đèn đều tắt thì phòng không có ánh sáng.

Vậy để phòng có ánh sáng thì có 64 – 1 = 63  cách bật, tắt các bóng đèn để căn phòng có ánh sáng.

Bài 4. Từ các chữ số 1; 2; 3; 5; 9 có thể lập được bao nhiêu số tự nhiên nhỏ hơn 200?

Lời giải:

+ Trường hợp 1: Số cần lập có 1 chữ số: có 5 số thỏa mãn là 1; 2; 3; 5; 9.

+ Trường hợp 2: Số cần lập có 2 chữ số.

Chọn chữ số hàng chục có: 5 cách.

Chọn chữ số hàng đơn vị có: 5 cách

Theo quy tắc nhân có: 5.5 = 25 số thỏa mãn.

+ Trường hợp 3: Số cần lập có 3 chữ số.

Chọn chữ số hàng trăm có 1 cách (chữ số hàng trăm phải là 1) – vì số cần lập nhỏ hơn 200.

Chọn chữ số hàng chục có: 5 cách.

Chọn chữ số hàng đơn vị có: 5 cách

Theo quy tắc nhân có: 1.5.5 = 25 số thỏa mãn.

Suy ra; số các số thỏa mãn đầu bài là: 5 + 25 + 25 = 55 số.

Bài 5. Có 5 bạn nam và 5 bạn nữ. Hỏi có bao nhiêu cách xếp sao cho hai bạn cùng giới không đứng cạnh nhau.

Lời giải:

Đánh số 10 vị trí xếp từ 1 đến 10.

+ Trường hợp 1. Các bạn nam xếp ở vị trí lẻ, các bạn nữ xếp ở vị trí chẵn.

Xếp 5 bạn nam vào 5 vị trí lẻ có 5! = 120 cách

Xếp 5 bạn nữ vào 5 vị trí chẵn có 5! = 120 cách

Theo quy tắc nhân có: 120.120 = 14400 cách.

+ Trường hợp 2. Các bạn nam xếp ở vị trí chẵn, các bạn nữ xếp ở vị trí lẻ.

Tương tự trường hợp 1; có 14400 cách.

Vậy có tất cả: 14 400 + 14 400 = 28 800 cách.

Bài 6. Có 6 học sinh lớp 11 và 3 học sinh lớp 12 sẽ ngồi trên một hàng ngang có 9 ghế. Hỏi có bao nhiêu cách xếp chỗ ngồi cho 9 học sinh đó sao cho mỗi học sinh lớp 12 ngồi giữa hai học sinh khối 11?

Lời giải :

Do mỗi học sinh lớp 12 ngồi giữa hai học sinh khối 11 nên ở vị trí đầu tiên và cuối cùng của dãy ghế sẽ là học sinh khối 11.

Bước 1: Xếp 6 học sinh lớp 11 thành một hàng ngang, có 6! cách.

Bước 2: giữa 6 bạn học sinh lớp 11 có 5 khoảng trống, chọn 3 khoảng trống trong 5 khoảng trống để xếp các bạn lớp 12, có $A_5^2$ cách (có liên quan đến thứ tự).

Theo quy tắc nhân có $6!.A_5^2=14400$ cách xếp thỏa yêu cầu.

Bài 7. Cho tập hợp A = {0; 1; 2; 3; 4; 5}. Có thể lập bao nhiêu số tự nhiên có 5 chữ số khác nhau?

Lời giải:

Xếp 5 phần tử của A vào 5 ô trống liền nhau, mỗi ô trống chỉ chứa 1 phần tử, không ô trống nào chứa cùng phần tử, số cách xếp ban đầu này là $A_6^5=720$  

Tương tự như vậy, nhưng mặc định ô trống đầu tiên là chứa phần tử 0, số cách xếp vào 4 ô trống còn lại tương ứng là $A_5^4=120$.

 Số các số tự nhiên có 5 chữ số khác nhau được lập từ tập A là 720 – 120 = 600.

Bài 8. Cho hai đường thẳng song song a và b. Trên đường thẳng a có 7 điểm phân biệt, trên đường thẳng b có 6 điểm phân biệt. Hỏi có bao nhiêu tam giác có đỉnh là các điểm đã cho.

Lời giải:

+ Trường hợp 1: Tam giác được tạo thành có 2 đỉnh thuộc đường thẳng a và 1 đỉnh thuộc đường thẳng b.

Chọn 2 đỉnh thuộc a có $C_7^2=21$ cách

Chọn 1 đỉnh thuộc b có 6 cách

Có 21.6 = 126 tam  giác.

+ Trường hợp 2: Tam giác được tạo thành có 2 đỉnh thuộc đường thẳng b và 1 điểm thuộc đường thẳng a.

Chọn 2 đỉnh thuộc b có $C_6^2=15$ cách

Chọn 1 đỉnh thuộc a có 7 cách

Có 15.7 = 105 tam  giác.

Số các tam giác thỏa mãn đầu bài là: 126 + 105 = 231.

Bài 9. Viết khai triển theo công thức nhị thức Niu- tơn.

a) (2x – 1)⁶.

b) (2x + 2y)⁵.

Lời giải:

Theo khai triển nhị thức Niu- tơn ta có:

a)

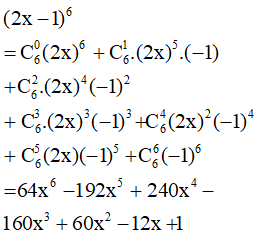
b)

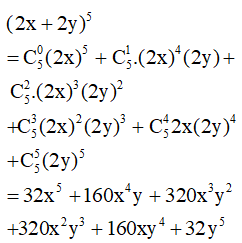
Bài 10. Tìm hệ số chứa x⁴ trong khai triển biểu thức ${\left(x-\frac{1}{x}\right)}^{10}$.

Lời giải:

Số hạng thứ k + 1 trong khai triển là:

$\begin{array}{l}{T}_{k+\text{}1}=C_{10}^k.x^{10-k}.{\left(\frac{-1}{x}\right)}^k\\ =C_{10}^k.{\left(-1\right)}^k.x^{10-2k}\end{array}$

Để số hạng này chứa x⁴ thì điều kiện là:

10 – 2k = 4 nên k = 3.

Vậy hệ số chứa x⁴ trong khai triển đã cho là: $C_{10}^3.{(-1)}^3=-120$.

Bài 11. Tìm số hạng thứ 8 trong khai triển (2x + 3y)¹²

Lời giải:

Số hạng thứ k + 1 trong khai triển là: 

$$\begin{gathered} T_{k+\text{}1}=C_{12}^k.{\left(2x\right)}^{12-k}.{\left(3y\right)}^k \\ =C_{12}^k.2^{12-k}{.3}^k.{\left(x\right)}^{12-k}.y^k \end{gathered}$$

Suy ra, số hạng thứ 8 trong khai triển ứng với k + 1 = 8 nên k = 7.

Vậy số hạng thứ 8 trong khai triển là:

$$\begin{gathered} T_8=C_{12}^7{.2}^5{.3}^7.x^5.y^7 \\ =55427328x^5.y^7 \end{gathered}$$

Bài 12. Biết hệ số của x³ trong khai triển của (2 – 4x)ⁿ là –10 240.  Tìm n.

Lời giải:

Số hạng thứ k + 1 trong khai triển là:

$$\begin{gathered} T_{k+1}=C_n^k{.2}^{n-k}.{(-4x)}^k \\ =C_n^k{.2}^{n-k}.{(-4)}^k{x}^k \end{gathered}$$

Để số hạng này chứa x³ thì k = 3.

Bài 13. Xét phép thử, gieo đồng tiền hai lần:

a) Mô tả không gian mẫu.

b) Xác định các biến cố:

A: “Lần đầu xuất hiện mặt sấp”.

B: “Hai lần xuất hiện giống nhau”.

C: “Có ít nhất một lần xuất hiện mặt ngửa”.

Lời giải:

a) Không gian mẫu là:  = {SS; SN; NS; NN}.

b) Các biến cố A; B; C là:

A = {SN; SS}.

B = {SS; NN}.

C = {NS; SN; NN} .

Bài 14. Gieo con súc sắc cân đối và đồng chất liên tiếp hai lần, xác định các biến cố sau:

A: “Tổng số chấm trong hai lần gieo lớn hơn 9”.

B: “Lần thứ nhất xuất hiện mặt 6 chấm”.

C: “Hiệu số chấm hai lần gieo là 2”.

Lời giải:

Ta xác định các biến cố:

A = {(5; 5); (5; 6); (6; 5); (6; 6)}.

B = {( 6; 1); (6; 2); (6; 3); (6; 4); (6; 5); (6; 6)}.

C = {(3; 1); (4; 2); (5; 3); (6; 4); (1; 3); (2; 4); (3; 5); (4; 6)}.

Bài 15. Một hộp đựng 8 thẻ, đánh số từ 1 đến 8. Chọn lần lượt ngẫu nhiên 3 thẻ. Xác định các biến cố sau:

A: “Tổng số của 3 thẻ được chọn không vượt quá 7”.

B: “Ba thẻ được chọn là ba số chẵn”

C: “Thẻ thứ nhất là 7 và tổng hai thẻ thứ 2; thứ 3 nhỏ hơn 5”.

Lời giải:

Ta xác định các biến cố:

A = {(1; 2; 3); (1; 3; 2); (2; 1; 3); (2; 3; 1); (3; 1; 2); (3; 2; 1); (1; 2; 4); (1; 4; 2);

 (2; 4; 1); (2; 1; 4); (4; 1; 2); (4; 2; 1)}.

B = {(2; 4; 6); (2; 6; 4); ( 4; 2; 6); (4; 6; 2); (6; 2; 4); (6; 4; 2)}.

C = {( 7; 1; 2) ; (7; 2; 1); (7; 1; 3); (7; 3; 1)}.

Bài 16. Trong một chiếc hộp đựng 6 viên bi đỏ, 8 viên bi xanh, 10 viên bi trắng. Lấy ngẫu nhiên 4 viên bi. Tính số phần tử của:

a) Không gian mẫu.

b) Các biến cố:

A: “4 viên bi lấy ra có đúng hai viên bi màu trắng”

B: “4 viên bi lấy ra có ít nhất một viên bi màu đỏ”

Lời giải:

a) Ta có: $n\left(\Omega \right)=C_{24}^4=10626$

b)

- Số cách chọn 4 viên bi có đúng hai viên bi màu trắng là: $C_{10}^2.C_{14}^2=4095$

Suy ra, số phần tử của biến cố A là 4095.

- Số cách lấy 4 viên bi mà không có viên bi màu đỏ được chọn là: $C_{18}^4$

Suy ra : số phần tử của biến cố B là $C_{24}^4-C_{18}^4=7566$.

Bài 17. Một hộp đựng 11 tấm thẻ được đánh số từ 1 đến 11. Chọn ngẫu nhiên 6 tấm thẻ. Tính xác suất để tổng số ghi trên 6 tấm thẻ ấy là một số lẻ?

Lời giải:

 Số phần tử của không gian mẫu là $n\left(\Omega \right)=C_{11}^6=462$.

Gọi biến cố A: “tổng số ghi trên 6 tấm thẻ ấy là một số lẻ”.

Từ 1 đến 11 có 6 số lẻ và 5 số chẵn.

Để có tổng là một số lẻ ta có 3 trường hợp.

-Trường hợp 1: Chọn được 1 thẻ mang số lẻ và 5 thẻ mang số chẵn có:

$6.C_5^5=6$ cách.

-Trường hợp 2: Chọn được 3 thẻ mang số lẻ và 3 thẻ mang số chẵn có:

$C_6^3.C_5^3=200$ cách.

-Trường hợp 3: Chọn được 5 thẻ mang số lẻ và 1 thẻ mang số chẵn có:

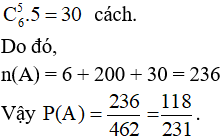
Bài 18. Một bình đựng 4 quả cầu xanh và 6 quả cầu trắng.

a) Chọn ngẫu nhiên 3 quả cầu. Tính xác suất để được 3 quả cầu toàn màu xanh.

b) Chọn ngẫu nhiên 4 quả cầu. Tính xác suất để được 2 quả cầu xanh và 2 quả cầu trắng.

Lời giải:

a) Phép thử : Chọn ngẫu nhiên ba quả cầu.

Ta có: $n\left(\Omega \right)=C_{10}^3=120$.

Biến cố A : Được ba quả toàn màu xanh.

$\Rightarrow n\left(A\right)=C_4^3=4$

 Xác suất để được 3 quả cầu toàn màu xanh là $P\left(A\right)=\frac{n\left(A\right)}{n\left(\Omega \right)}=\frac{1}{30}$.

b)

Phép thử : Chọn ngẫu nhiên bốn quả cầu.

Ta có $n\left(\Omega \right)=C_{10}^4=210$.

Biến cố B: Được hai quả xanh, hai quả trắng

$\Rightarrow n\left(B\right)=C_4^2.C_6^2=90$

 Xác suất để được 2 quả cầu xanh và 2 quả cầu trắng

$P\left(B\right)=\frac{n\left(B\right)}{n\left(\Omega \right)}=\frac{3}{7}$

Bài 19. Một đội gồm 5 nam và 8 nữ. Lập một nhóm gồm 4 người đi biểu diễn văn nghệ. Tính xác suất để trong 4 người được chọn có ít nhất 3 nữ.

Lời giải:

Không gian mẫu là chọn tùy ý 4 người từ 13 người.

Suy ra số phần tử của không gian mẫu là $n\left(\Omega \right)=C_{13}^4=715$

Gọi A là biến cố “4 người được chọn có ít nhất 3 nữ”.

Ta có hai trường hợp thuận lợi cho biến cố A như sau:

- TH1: Chọn 3 nữ và 1 nam, có $C_8^3.C_5^1=280$ cách.

Bài 20. Một hộp có 5 viên bi xanh, 6 viên bi đỏ và 7 viên bi vàng. Chọn ngẫu nhiên 5 viên bi trong hộp. Tính xác suất để 5 viên bi được chọn có đủ màu và số bi đỏ bằng số bi vàng.

Lời giải:

Hộp bi có tất cả: 5 + 6 + 7 = 18 viên bi.

Không gian mẫu là số cách chọn ngẫu nhiên 5 viên bi từ hộp chứa 18 viên bi.

Suy ra số phần tử của không gian mẫu là $n\left(\Omega \right)=C_{18}^5=8568$.

Gọi A là biến cố “5 viên bi được chọn có đủ màu và số bi đỏ bằng số bi vàng’.

Ta có các trường hợp thuận lợi cho biến cố A là:

- TH1: Chọn 1 bi đỏ, 1 bi vàng và 3 bi xanh nên có $C_6^1.C_7^1.C_5^3=420$ cách.

- TH2: Chọn 2 bi đỏ, 2 bi vàng và 1 bi xanh nên có $C_6^2.C_7^2.C_5^1=1575$ cách.

Suy ra số phần tử của biến cố A là n(A) = 420 + 1575 = 1995.

Vậy xác suất cần tính $P\left(A\right)=\frac{1995}{8568}=\frac{95}{408}$.

Trắc nghiệm Toán 11 Bài: Ôn tập chương 2

Câu 1: Bất phương trình $C_{n-1}^4-C_{n-1}^3-\frac{5}{4}{A}_{n-2}^2<0$ có bao nhiêu nghiệm?

A. 11

B. 13

C. 6

D. Vô số

Câu 2: Sắp xếp năm bạn học sinh An, Bình, Chi, Dũng, Lệ vào một chiếc ghế dài có 5 chỗ ngồi. Số cách sắp xếp sao cho bạn Chi luôn ngồi chính giữa là

A. 16

B. 60

C. 24

D. 120

Câu 3: Một hộp chứa chín chiếc thẻ được đánh số từ 1 đến 9. Lấy ngẫu nhiên (đồng thời) hai thẻ. Số phần tử của không gian mẫu là

A. 81

B. 9

C. 36

D. 72

Câu 4: Cho $A=\left\{1;2;3;5;7\right\}$. Từ tập A có thể lập được bao nhiêu số tự nhiên gồm ba chữ số đôi một khác nhau?

A. 24

B. 10

C. 125

D. 60

Câu 5: Sắp xếp 6 nam sinh và 4 nữ sinh vào một dãy ghế hàng ngang có 10 chỗ ngồi. Hỏi có bao nhiêu cách sắp xếp sao cho các nữ sinh luôn ngồi cạnh nhau?

A. 207360

B. 17280

C. 120960

D. 34560

Câu 6: Từ một hộp đựng 30 thẻ được đánh số từ 1 đến 30, rút ngẫu nhiên 10 thẻ. Gọi A là biến cố rút được 5 thẻ đánh số lẻ, 5 thẻ đánh số chẵn và có đúng hai thẻ có số chia hết cho 10. Tìm số phần tử của A .

A.  $C_{13}^3.C_{15}^5.$

B.   $3.C_{13}^3.C_{15}^5.$

C.   $3.C_{12}^3.C_{15}^5.$

D.   $C_{12}^3.C_{15}^5.$

Câu 7: Cho hai đường thẳng song song $d_1$, $d_2$. Trên $d_1$ lấy 5 điểm phân biệt tô màu xanh, trên $d_2$ lấy 8 điểm phân biệt tô màu đỏ. Xét tất cả các tam giác có đỉnh lấy từ các điểm trên. Chọn ngẫu nhiên một tam giác. Tính xác suất để tam giác được chọn có đúng hai đỉnh màu xanh.

A. $\frac{5}{11}$

B. $\frac{5}{143}$

C. $\frac{7}{11}$

D. $\frac{4}{11}$

Câu 8: Đội học sinh giỏi cấp trường môn Tiếng Anh của trường THPT chuyên Vĩnh Phúc gồm 8 học sinh khối 10, 8 học sinh khối 11 và 8 học sinh khối 12. Nhà trường cần chọn 10 học sinh tham gia câu lạc bộ tiếng Anh của trường. Tính số cách chọn sao cho có học sinh cả ba khối và có nhiều nhất 2 học sinh khối 10.

A. 1961256.

B. 451824.

C. 451880.

D. 459888.

Câu 9: Có 3 xạ thủ bắn độc lập vào bia. Xác suất bắn trúng của mỗi xạ thủ lần lượt là 0,6; 0,8 và 0,9. Tính xác suất để trong 3 xạ thủ có đúng 2 xạ thủ bắn trúng bia.

A. 0,568.

B. 0,876.

C. 0,7.

D. 0,444.

Câu 10: Hệ số $x^7$ của trong khai triển ${\left(4-x\right)}^9$ là

A. $9C_9^7.$

B. $-16C_9^7.$

C. $-9C_9^7.$

D. $16C_9^7.$

Xem thêm các bài tổng hợp lý thuyết Toán lớp 11 đầy đủ, chi tiết khác:

Lý thuyết Phương pháp quy nạp toán học 

Lý thuyết Dãy số

Lý thuyết Cấp số cộng

Lý thuyết Cấp số nhân 

Lý thuyết Ôn tập chương 3