Lý thuyết Phép đối xứng trục (mới 2023 + Bài Tập) - Toán 11

Lý thuyết Toán 11 Bài 3: Phép đối xứng trục

Bài giảng Toán 11 Bài 3: Phép đối xứng trục

A. Lý thuyết.

I. Định nghĩa.

- Cho đường thẳng d. Phép biến hình biến mỗi điểm M thuộc d thành chính nó, biến mỗi điểm M không thuộc d thành điểm M’ sao cho d là đường trung trực của đoạn MM’ được gọi là phép đối xứng qua đường thẳng d hay phép đối xứng trục d.

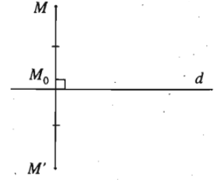
Đường thẳng d được gọi là trục của phép đối xứng hoặc đơn giản là trục đối xứng.

Phép đối xứng trục d thường được kí hiệu là Đ_d.

- Nếu hình ℋ ' là ảnh của hình ℋ  qua phép đối xứng trục d thì ta còn nói ℋ  đối xứng với ℋ ' qua d, hay ℋ  và ℋ ' đối xứng với nhau qua d.

- Nhận xét:

1) Cho đường thẳng d. Với mỗi điểm M, gọi M₀ là hình chiếu vuông góc của M

trên đường thẳng d. Khi đó: M’ = Đ_d(M) $\iff \overrightarrow{M_{0}M\text{'}}=-\overrightarrow{M_{0}M}$

2) M’ = Đ_d(M) $\iff$M = Đ_d(M’).

II. Biểu thức tọa độ.

1) Chọn hệ trục tọa độ Oxy sao cho trục Ox trùng với đường thẳng d. Với mỗi điểm M = (x ; y), gọi M’ = Đ_d(M) = (x’ ; y’) thì $\left\{\begin{array}{c}x\text{'}=x\\ y\text{'}=-y\end{array}\right.$, đây là biểu thức tọa độ của phép đối xứng qua trục Ox. 

2) Chọn hệ trục tọa độ Oxy sao cho trục Oy trùng với đường thẳng d. Với mỗi điểm M = (x ; y), gọi M’ = Đ_d(M) = (x’; y’) thì $\left\{\begin{array}{c}x\text{'}=-x\\ y\text{'}=y\end{array}\right.$, đây là biểu thức tọa độ của phép đối xứng qua trục Oy.

Ví dụ 1. Cho điểm M(2 ; 4). Tìm ảnh của điểm M qua phép đối xứng qua trục Ox và trục Oy.

Lời giải:

Gọi Đ_Ox(M) = A(x ; y) và Đ_Oy(M) = B(a; b)

Áp dụng biểu thức tọa độ của phép đối xứng trục Ox ta có:

$$\begin{gathered} \left\{\begin{array}{c}x=2\\ y=-4\end{array}\right. \\ \Rightarrow A(2;-4) \end{gathered}$$

Áp dụng biểu thức tọa độ của phép đối xứng trục Oy ta có:

$\left\{\begin{array}{c}a=-2\\ b=4\end{array}\Rightarrow B(-2;4)\right.$

III. Tính chất.

- Tính chất 1. Phép đối xứng trục bảo toàn khoảng cách giữa hai điểm bất kì.

- Tính chất 2. Phép đối xứng trục biến đường thẳng thành đường thẳng, biến đoạn thẳng thành đoạn thẳng bằng nó, biến tam giác thành tam giác bằng nó, biến đường tròn thành đường tròn có cùng bán kính.

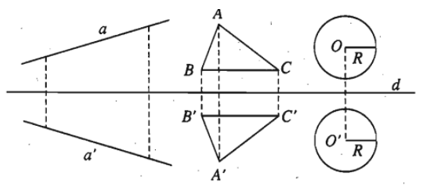
Ví dụ 2. Trong mặt phẳng tọa độ Oxy, qua phép đối xứng trục Ox, đường tròn (C)

(x – 2)² + (y – 3)² = 36 biến thành đường tròn (C’). Tìm phương trình đường tròn (C’) ?

Lời giải:

Đường tròn (C) có tâm I(2 ; 3) và bán kính là R = 6.

Qua phép đối xứng trục Ox, biến đường tròn (C) thành đường tròn (C’), biến tâm I thành tâm I’(x’; y’) và bán kính R’ = R = 6.

Áp dụng biểu thức phép đối xứng trục Ox ta được I’(2; – 3)

Do đó, phương trình đường tròn (C’) là:

(x – 2)² + (y + 3)² = 36.

IV. Trục đối xứng của một hình

- Định nghĩa. Đường thẳng d được gọi là trục đối xứng của hình ℋ nếu phép đối xứng qua đường thẳng d biến ℋ thành chính nó.

Khi đó, ta nói ℋ là hình có trục đối xứng.

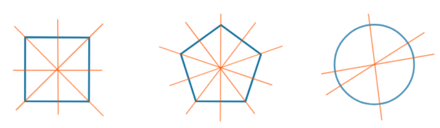
- Ví dụ 3. Các hình sau có trục đối xứng

B. Bài tập tự luyện

Bài 1. Mỗi hình sau có bao nhiêu trục đối xứng?

a) Hình gồm hai đường tròn có tâm và bán kính khác nhau.

b) Hình gồm hai đường thẳng d và d’ vuông góc với nhau.

c) Hình gồm 3 đường tròn có bán kính bằng nhau và đôi một tiếp xúc ngoài với nhau.

Lời giải:

Một đường tròn có vô số trục đối xứng đi qua tâm của đường tròn đó.

Do đó, trục đối xứng thỏa yêu cầu của bài toán là đường thẳng nối hai tâm của đường tròn đã cho.

Vậy hình gồm hai đường tròn có tâm và bán kính khác nhau có 1 trục đối xứng.

b) Có bốn trục đối xứng gồm đường thẳng d; d’ và hai đường phân giác của hai góc tạo bởi d, d’.

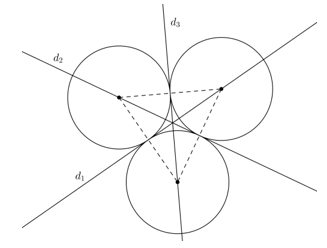
c) Có 3 trục đối xứng là 3 đường trung trực của các đoạn nối tâm.

Bài 2. Trong mặt phẳng Oxy, cho điểm M(2 ; 3). Tìm ảnh của M qua phép đối xứng qua đường thẳng d: x – y = 0?

Lời giải:

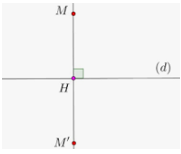
Gọi H là hình chiếu vuông góc của M trên d.

Ta có đường thẳng MH vuông góc với d nên đường thẳng MH có vectơ chỉ phương là:

$$\begin{gathered} \overrightarrow{u_{MH}}=\overrightarrow{n_d}=(1;-1) \\ \Rightarrow \overrightarrow{n_{MH}}=(1;1) \end{gathered}$$

Phương trình đường thẳng MH: 1.(x – 2) + 1.(y – 3) = 0 hay x + y – 5 = 0

Hai đường thẳng MH và d cắt nhau tại H nên tọa độ H là nghiệm hệ:

$\begin{array}{l}\left\{\begin{array}{c}x-y=0\\ x+y-5=0\end{array}\right.\\ \iff x=y=\frac{5}{2}\\ \Rightarrow H\left(\frac{5}{2};\frac{5}{2}\right)\end{array}$

Vì Đ_d(M) = M’ nên H là trung điểm của MM’.

$$\begin{gathered} \Rightarrow \left\{\begin{array}{c}{x}_{M\text{'}}=2x_H-x_M=3\\ y_{M\text{'}}=2y_H-y_M=2\end{array}\right. \\ \Rightarrow M\text{'}\left(3;2\right) \end{gathered}$$

Vậy M’(3; 2).

Bài 3. Trong mặt phẳng với hệ trục tọa độ Oxy, cho phép đối xứng trục Ox biến đường thẳng d: x + y – 2 = 0 thành đường thẳng d’. Viết phương trình d’.

Lời giải:

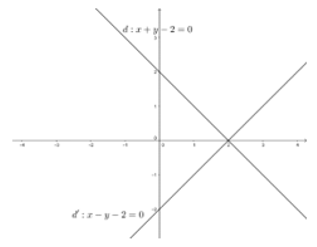
Lấy điểm M(x ; y) thuộc d suy ra:

x + y – 2 = 0  (1)

Gọi M’(x’; y’) là ảnh của M qua phép đối xứng trục Ox.

Khi đó ta có: $\left\{\begin{array}{c}x\text{'}=x\\ y\text{'}=-y\end{array}\right.$$\hspace{0.17em}\Rightarrow \left\{\begin{array}{c}x=x\text{'}\\ y=-y\text{'}\end{array}\right.$.  (2)

Thay (2) vào (1) ta được :

x’ – y’ – 2 = 0

Suy ra, phương trình đường thẳng d’ : x – y – 2 = 0.

Bài 4. Trong mặt phẳng tọa độ Oxy, cho đường thẳng đường tròn (C):

x² + y² – 2x – 4y – 4 =  0. Tìm ảnh của (C) qua phép đối xứng trục Oy.

Lời giải:

Đường tròn (C) có tâm I(1; 2) và bán kính $R=\sqrt{1^2+\text{\hspace{0.17em}\hspace{0.17em}}{2}^2-(-4)}=3$.

Gọi I’ và R’ là tâm và bán kính của (C’) là ảnh của đường tròn (C) qua phép đối xứng trục Oy.

Ta có: R’ = R = 3

Ta tìm tọa độ tâm I’.

Áp dụng biểu thức tọa độ của phép đối xứng trục Oy ta được I’(– 1; 2)

Phương trình đường tròn (C’): (x + 1)² + (y – 2)² = 9.

Trắc nghiệm Toán lớp 11 Bài 3: Phép đối xứng trục

Câu 1. Tam giác đều có bao nhiêu trục đối xứng?

A. 0

B. 1

C. 3

D. Vô số.

Hiển thị đáp án  

Đáp án: C

Giải thích:

Tam giác đều có 3 trục đối xứng (đường thẳng đi qua đỉnh tam giác và trung điểm cạnh đối diện).

Câu 2. Trong mặt phẳng tọa độ  cho đường thẳng  có phương trình $3x+y-1=0$. Xét phép đối xứng trục $\Delta :2x-y+1=0$, đường thẳng d biến thành đường thẳng $d\text{'}$ có phương trình là:

A. $3x-y+1=0.$

B. $x+3y-3=0.$

C. $x-3y+3=0.$

D. $x+3y+1=0.$

Hiển thị đáp án  

Đáp án: C

Giải thích:

Tọa độ giao điểm A của d và $∆$ thỏa mãn hệ $\left\{\begin{array}{l}3x+y-1=0\\ 2x-y+1=0\end{array}\right.\Rightarrow A\left(0;1\right).$

Vì $A\in \Delta$ nên qua phép đối xứng trục $∆$ biến thành chính nó, tức $A\text{'}\equiv A\left(0;1\right).$

Chọn điểm $B\left(1;-2\right)\in d$.

Đường thẳng đi qua điểm B và vuông góc với $∆$ có phương trình $\mathcal{l}:x+2y+3=0$.

Gọi $H=\Delta \cap \mathcal{l}$, suy ra tọa độ điểm H thỏa hệ $\left\{\begin{array}{l}2x-y+1=0\\ x+2y+3=0\end{array}\right.\Rightarrow H\left(-1;-1\right).$

Gọi $B\text{'}\left(x\text{'};y\text{'}\right)$ là điểm đối xứng của B qua $\Delta$$\to H$ là trung điểm của $BB\text{'}$

$\iff \left\{\begin{array}{l}x\text{'}=2x_H-x_B\\ y\text{'}=2y_H-y_B\end{array}\right.$

$\Rightarrow \left\{\begin{array}{l}x\text{'}=-3\\ y\text{'}=0\end{array}\right.$

$\Rightarrow B\text{'}\left(-3;0\right).$

Đường thẳng $d\text{'}$ cần tìm đi qua hai điểm $A\text{'},B\text{'}$ nên có phương trình $x-3y+3=0.$

Câu 3. Trong mặt phẳng tọa độ $Oxy$ cho đường tròn $\left(C\right):{\left(x+1\right)}^2+{\left(y-4\right)}^2=1$ và đường thẳng d có phương trình $y-x=0.$ Phép đối xứng trục d biến đường tròn $\left(C\right)$  thành đường tròn $\left(C\text{'}\right)$ có phương trình là:

A. ${\left(x+1\right)}^2+{\left(y-4\right)}^2=1.$

B. ${\left(x-4\right)}^2+{\left(y+1\right)}^2=1.$

C. ${\left(x+4\right)}^2+{\left(y-1\right)}^2=1.$

D. ${\left(x+4\right)}^2+{\left(y+1\right)}^2=1.$ 

Hiển thị đáp án  

Đáp án: B

Giải thích:

Biểu thức tọa độ của phép đối xứng qua trục $d:y-x=0$ (đường phân giác góc phần tư thứ nhất) là $\left\{\begin{array}{c}x\text{'}=y\\ y\text{'}=x\end{array}\right.$.

Thay vào $\left(C\right)$, ta được ${\left(y\text{'}+1\right)}^2+{\left(x\text{'}-4\right)}^2=1$ hay  ${\left(x-4\right)}^2+{\left(y+1\right)}^2=1.$

Câu 4. Trong các mệnh đề sau, mệnh đề nào đúng?

A. Tam giác có trục đối xứng.

B. Tứ giác có trục đối xứng.

C. Hình thang có trục đối xứng.

D. Hình thang cân có trục đối xứng.

Hiển thị đáp án  

Đáp án: D

Giải thích:

Hình thang cân có trục đối xứng (đường thẳng đi qua trung điểm của hai cạnh đáy).

Câu 5. Trong các hình dưới đây, hình nào có nhiều trục đối xứng nhất?

A. Đoạn thẳng.

B. Đường tròn.

C. Tam giác đều.

D. Hình vuông.

Hiển thị đáp án  

Đáp án: B

Giải thích:

Đoạn thẳng có 1 trục đối xứng là đường trung trực của đoạn thẳng.

Đường tròn có vô số trục đối xứng là các đường thẳng đi qua tâm.

Tam giác đều có 3 trục đối xứng là các đường thẳng đi qua đỉnh và trung điểm cạnh đối diện.

Hình vuông có 4 trục đối xứng.

Vậy hình tròn có nhiều trục đối xứng nhất.

Câu 6. Xem các chữ cái in hoa A, B, C, D, X, Y như những hình. Khẳng định nào sau đây đúng?

A. Hình có một trục đối xứng là: A, Y. Các hình khác không có trục đối xứng.

B. Hình có một trục đối xứng: A, B, C, D, Y. Hình có hai trục đối xứng: X.

C. Hình có một trục đối xứng: A, B. Hình có hai trục đối xứng: D, X.

D. Hình có một trục đối xứng: C, D, Y. Hình có hai trục đối xứng: X. Các hình khác không có trục đối xứng.

Hiển thị đáp án  

Đáp án: B

Câu 7. Hình gồm hai đường tròn có tâm và bán kính khác nhau có bao nhiêu trục đối xứng?

A. 0

B. 1

C. 2

D. Vô số.

Hiển thị đáp án  

Đáp án: B

Giải thích:

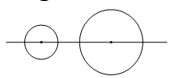
Có duy nhất một trục đối xứng đi qua tâm của hai đường tròn.

Câu 8. Cho ba đường tròn có bán kính bằng nhau và đôi một tiếp xúc ngoài với nhau tạo thành hình H. Hỏi H có mấy trục đối xứng?

A. 0

B.  1

C.  2

D.  3

Hiển thị đáp án  

Đáp án: D

Giải thích:

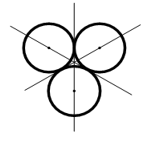
Có 3 trục đối xứng như hình vẽ.

Câu 9. Mệnh đề nào sau đây sai?

A. Hình gồm hai đường tròn không bằng nhau có trục đối xứng.

B. Hình gồm một đường tròn và một đoạn thẳng tùy ý có trục đối xứng.

C. Hình gồm một đường tròn và một đường thẳng tùy ý có trục đối xứng.

D. Hình gồm một tam giác cân và đường tròn ngoại tiếp tam giác đó có trục đối xứng.

Hiển thị đáp án  

Đáp án: B

Giải thích:

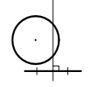
Trường hợp trục đối xứng của đoạn thẳng không đi qua tâm của đường tròn như hình vẽ.

Câu 10. Có bao nhiêu phép đối xứng trục biến một đường thẳng d cho trước thành chính nó?

A. Không có phép nào.

B. Có một phép duy nhất.

C. Chỉ có hai phép.

D. Có vô số phép.

Hiển thị đáp án  

Đáp án: D

Giải thích:

Gọi $∆$ là đường thẳng vuông góc với đường thẳng d 

Khi đó, phép đối xứng trục $∆$ biến d thành chính nó.

Có vô số đường thẳng $∆$ vuông góc với d

Xem thêm các bài tổng hợp lý thuyết Toán lớp 11 đầy đủ, chi tiết khác:

Lý thuyết Phép đối xứng tâm

Lý thuyết Phép quay

Lý thuyết Khái niệm về phép dời hình và hai hình bằng nhau

Lý thuyết Phép vị tự 

Lý thuyết Phép đồng dạng