Lý thuyết Phép thử và biến cố (mới 2023 + Bài Tập) – Toán 11

Lý thuyết Toán 11 Bài 4: Phép thử và biến cố

Bài giảng Toán 11 Bài 4: Phép thử và biến cố

A. Lý thuyết

I. Phép thử, không gian mẫu

1. Phép thử.

Một trong những khái niệm cơ bản của lí thuyết xác suất là phép thử. Một thí nghiệm, một phép đo, hay một sự quan sát hiện tượng nào đó… được hiểu là phép thử.

- Ví dụ 1. Gieo ba đồng tiền xu liên tiếp, chọn ba cây tú lơ khơ từ bộ bài 52 cây tứ lơ khơ, chọn 3 bông hoa từ 10 bông hoa trong lọ… đây đều là phép thử.

- Khi gieo một đồng tiền, ta không thể đoán trước được mặt xuất hiện là sấp hay ngửa. Đó là ví dụ về phép thử ngẫu nhiên.

- Tổng quát. Phép thử ngẫu nhiên là phép thử mà ta không đoán trước được kết quả của nó, mặc dù đã biết tập hợp tất cả các kết quả có thể có của phép thử đó.

2. Không gian mẫu.

Tập hợp các kết quả có thể xảy ra của một phép thử được gọi là không gian mẫu của phép thử và kí hiệu là $\Omega$ (đọc là ô-mê-ga).

- Ví dụ 2. Nếu phép thử là gieo một con súc sắc một lần, thì không gian mẫu gồm 6 phần tử là: $\Omega$ = {1; 2; 3; 4; 5; 6}.

- Ví dụ 3. Nếu phép thử là gieo một đồng tiền ba lần thì không gian mẫu gồm tám phần tử là:

{SSS; SSN; SNS; SNN; NSS; NSN; NNS; NNN} .

II. Biến cố.

- Một cách tổng quát, mỗi biến cố liên quan đến một phép thử được mô tả bởi một tập con của không gian mẫu.

- Định nghĩa: Biến cố là một tập con của không gian mẫu.

Ta thường kí hiệu các biến cố bằng các chữ in hoa A; B; C…

- Tập $\varnothing$ được gọi là biến cố không thể (gọi tắt là biến cố không). Còn tập  được gọi là biến cố chắc chắn.

- Ví dụ 4. Gieo con súc sắc liên tiếp hai lần thì biến cố: “lần thứ nhất ra mặt 5 chấm, lần thứ 2 ra mặt 8 chấm” là biến cố không. (vì súc sắc không có mặt 8 chấm)

Còn biến cố: “Tổng số chấm hai lần gieo lớn hơn 1 và nhỏ hơn 13” là biến cố chắc chắn.

- Ta nói rằng biến cố A xảy ra trong một phép thử nào đó khi và chỉ khi các kết quả của phép thử đó là một phần tử của A (hay thuận lợi cho A).

Như vậy, biến cố không thể không bao giờ xảy ra. Trong khi đó, biến cố chắc chắn luôn luôn xảy ra.

III. Phép toán trên các biến cố.

Giả sử A là biến cố liên quan đến một phép thử

- Tập $\Omega$\A được gọi là biến cố đối của biến cố A, kí hiệu là $\overline{A}$.

$\overline{A}$ xảy ra khi và chỉ khi A không xảy ra.

- Ví dụ 5. Nếu phép thử là chọn một học sinh trong lớp làm lớp trường thì:

Biến cố A: “bạn đó là nữ”.

Biến cố B: “bạn đó là nam”.

Ta thấy, B là biến cố đối của biến cố A: $B=\overline{A}$.

 - Giả sử A và B là hai biến cố liên quan đến một phép thử. Ta có định nghĩa:

Tập $A\cup B$ được gọi là hợp của các biến cố A và B.

Tập $A\cap B$ được gọi là giao của các biến cố A và B.

Nếu $A\cap B=\varnothing$ thì ta còn nói A và B xung khắc.

- Biến cố $A\cup B$ xảy ra khi và chỉ khi A xảy ra hoặc B xảy ra.

Biến cố $A\cap B$ xảy ra khi và chỉ khi A và B đồng thời xảy ra.

Biến cố $A\cap B$ còn được viết là A.B.

A và B xung khắc khi và chỉ khi chúng không khi nào cùng xảy ra.            

- Ta có bảng sau:

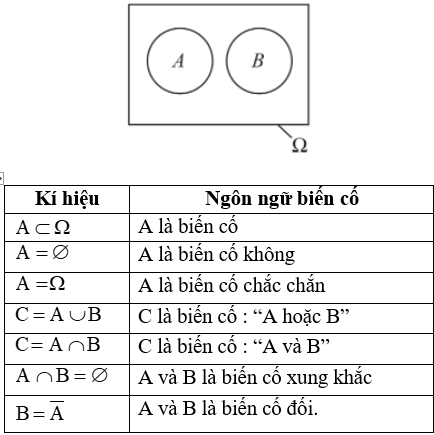
- Ví dụ 6. Xét phép thử: gieo súc sắc hai lần liên tiếp, với các biến cố:

A: “Kết quả hai lần gieo giống nhau”.

B. “Lần đầu xuất hiện mặt 5 chấm”.

Liệt kê các kết quả thuận lợi cho các biến A và B.

Lời giải:

A = {(1; 1); (2; 2); (3; 3); (4; 4); (5; 5); (6; 6)}.

B = {(5; 1); (5; 2); (5; 3); (5; 4); (5; 5); (5; 6)}.

B. Bài tập tự luyện

Bài 1. Xét phép thử, gieo đồng tiền hai lần:

a) Mô tả không gian mẫu.

b) Xác định các biến cố:

A: “Lần đầu xuất hiện mặt sấp”.

B: “Hai lần xuất hiện giống nhau”.

C: “Có ít nhất một lần xuất hiện mặt ngửa”.

Lời giải:

a) Không gian mẫu là:  = {SS; SN; NS; NN}.

b) Các biến cố A; B; C là:

A = {SN; SS}.

B = {SS; NN}.

C = {NS; SN; NN} .

Bài 2. Gieo con súc sắc cân đối và đồng chất liên tiếp hai lần, xác định các biến cố sau:

A: “Tổng số chấm trong hai lần gieo lớn hơn 9”.

B: “Lần thứ nhất xuất hiện mặt 6 chấm”.

C: “Hiệu số chấm hai lần gieo là 2”.

Lời giải:

Ta xác định các biến cố:

A = {(5; 5); (5; 6); (6; 5); (6; 6)}.

B = {( 6; 1); (6; 2); (6; 3); (6; 4); (6; 5); (6; 6)}.

C = {(3; 1); (4; 2); (5; 3); (6; 4); (1; 3); (2; 4); (3; 5); (4; 6)}.

Bài 3. Một hộp đựng 8 thẻ, đánh số từ 1 đến 8. Chọn lần lượt ngẫu nhiên 3 thẻ. Xác định các biến cố sau:

A: “Tổng số của 3 thẻ được chọn không vượt quá 7”.

B: “Ba thẻ được chọn là ba số chẵn”

C: “Thẻ thứ nhất là 7 và tổng hai thẻ thứ 2; thứ 3 nhỏ hơn 5”.

Lời giải:

Ta xác định các biến cố:

A = {(1; 2; 3); (1; 3; 2); (2; 1; 3); (2; 3; 1); (3; 1; 2); (3; 2; 1); (1; 2; 4); (1; 4; 2);

 (2; 4; 1); (2; 1; 4); (4; 1; 2); (4; 2; 1)}.

B = {(2; 4; 6); (2; 6; 4); ( 4; 2; 6); (4; 6; 2); (6; 2; 4); (6; 4; 2)}.

C = {( 7; 1; 2) ; (7; 2; 1); (7; 1; 3); (7; 3; 1)}.

Bài 4. Trong một chiếc hộp đựng 6 viên bi đỏ, 8 viên bi xanh, 10 viên bi trắng. Lấy ngẫu nhiên 4 viên bi. Tính số phần tử của:

a) Không gian mẫu.

b) Các biến cố:

A: “4 viên bi lấy ra có đúng hai viên bi màu trắng”

B: “4 viên bi lấy ra có ít nhất một viên bi màu đỏ”

Lời giải:

a) Ta có: $n\left(\Omega \right)=C_{24}^4=10626$

b)

- Số cách chọn 4 viên bi có đúng hai viên bi màu trắng là: $C_{10}^2.C_{14}^2=4095$

Suy ra, số phần tử của biến cố A là 4095.

- Số cách lấy 4 viên bi mà không có viên bi màu đỏ được chọn là: $C_{18}^4$

Suy ra : số phần tử của biến cố B là $C_{24}^4-C_{18}^4=7566$.

Trắc nghiệm Toán 11 Bài 4: Phép thử và Biến cố

Câu 1: Trong các thí nghiệm sau thí nghiệm nào không phải là phép thử ngẫu nhiên:

A. Gieo đồng tiền xem nó mặt ngửa hay mặt sấp

B. Gieo  đồng tiền và xem có mấy đồng tiền lật ngửa

C. Chọn bất kì 1 học sinh trong lớp và xem là nam hay nữ

D. Bỏ hai viên bi xanh và ba viên bi đỏ trong một chiếc hộp, sau đó lấy từng viên một để đếm xem có tất cả bao nhiêu viên bi.

Hiển thị đáp án  

Đáp án: D

Giải thích:

Phép thử ngẫu nhiên là phép thử mà ta chưa biết được kết quả là gì.

Đáp án D không phải là phép thử vì ta biết chắc chắn kết quả chỉ có thể là một số cụ thể số bi xanh và số bi đỏ.

Câu 2: Gieo 3 đồng tiền là một phép thử ngẫu nhiên có không gian mẫu là:

A. $\left\{NN,NS,SN,SS\right\}$

B. $\left\{\begin{array}{l}NNN,SSS,NNS,\\ SSN,NSN,SNS\end{array}\right\}$

C. $\left\{\begin{array}{l}NNN,SSS,NNS,SSN,\\ NSN,SNS,NSS,SNN\end{array}\right\}$

D. $\left\{\begin{array}{l}NNN,SSS,NNS,\\ SSN,NSS,SNN\end{array}\right\}$

Hiển thị đáp án  

Đáp án: C

Giải thích:

Liệt kê các phần tử.

Câu 3: Cho phép thử có không gian mẫu $\Omega =\left\{1,2,3,4,5,6\right\}$. Các cặp biến cố không đối nhau là:

A. $A=\left\{1\right\}$ và $B=\left\{2,3,4,5,6\right\}$

B. $C\left\{1,4,5\right\}$ và $D=\left\{2,3,6\right\}$

C. $E=\left\{1,4,6\right\}$ và $F=\left\{2,3\right\}$

D. $\Omega$ và $\varnothing$

Hiển thị đáp án  

Đáp án: C

Giải thích:

Cặp biến cố không đối nhau là $E=\left\{1,4,6\right\}$ và $F=\left\{2,3\right\}$ do $E\cap F=\varnothing$ và $E\cup F\ne \Omega$.

Câu 4: Một hộp đựng 10 thẻ, đánh số từ 1 đến 10. Chọn ngẫu nhiên  thẻ. Gọi A là biến cố để tổng số của 3 thẻ được chọn không vượt quá 8. Số phần tử của biến cố  là:

A. 2

B. 3

C. 4

D. 5

Hiển thị đáp án  

Đáp án: C

Giải thích:

Liệt kê ta có:

$A=\left\{\begin{array}{l}\left(1;2;3\right);\left(1;2;4\right);\left(1;2;5\right);\\ \left(1;3;4\right)\end{array}\right\}$

Câu 5: Xét phép thử tung con súc sắc 6 mặt hai lần. Xác định số phần tử của không gian mẫu

A. 36

B. 40

C. 38

D. 35

Hiển thị đáp án  

Đáp án: A

Giải thích:

Không gian mẫu gồm các bộ $(i;j)$, trong đó $i,j\in \left\{1,2,3,4,5,6\right\}$

 i nhận 6 giá trị, j cũng nhận 6 giá trị nên có $6.6=36$ bộ $(i;j)$

Vậy $\Omega =\left\{(i,j)|i,j=1,2,3,4,5,6\right\}$ và $n\left(\Omega \right)=36$.

Câu 6: Có 100 tấm thẻ được đánh số từ 1 đến 100. Lấy ngẫu nhiên 5 thẻ. Tính số phần tử của không gian mẫu:

A.  $n\left(\Omega \right)=C_{100}^5$

B.  $n\left(\Omega \right)=A_{100}^5$

C.  $n\left(\Omega \right)=C_{100}^1$

D.  $n\left(\Omega \right)=A_{100}^1$

Hiển thị đáp án  

Đáp án: A

Giải thích:

Ta có $n\left(\Omega \right)=C_{100}^5$

Câu 7: Trong một chiếc hộp đựng 6 viên bi đỏ, 8 viên bi xanh, 10 viên bi trắng. Lấy ngẫu nhiên 4 viên bi. Tính số phần tử của không gian mẫu:

A. 10626

B. 14241

C. 14284

D. 31311

Hiển thị đáp án  

Đáp án: A

Giải thích:

Ta có: $n\left(\Omega \right)=C_{24}^4=10626$

Câu 8: Một xạ thủ bắn liên tục 4 phát đạn vào bia. Gọi $A_k$ là các biến cố “ xạ thủ bắn trúng lần thứ k ” với $k=1,2,3,4$. Hãy biểu diễn các biến cố sau qua các biến cố $A_1,A_2,A_3,A_4$

A: “Lần thứ tư mới bắn trúng bia’’

A.  $A=\overline{A_1}\cap \overline{A_2}\cap A_3\cap A_4$

B.  $A=A_1\cap \overline{A_2}\cap \overline{A_3}\cap A_4$

C.   $A=\overline{A_1}\cap A_2\cap \overline{A_3}\cap A_4$

D.  $A=\overline{A_1}\cap \overline{A_2}\cap \overline{A_3}\cap A_4$

Hiển thị đáp án  

Đáp án: D

Giải thích:

Ta có: $\overline{A_k}$ là biến cố lần thứ k ( $k=1,2,3,4$ ) bắn không trúng bia.

Do đó: 

$A=\overline{A_1}\cap \overline{A_2}\cap \overline{A_3}\cap A_4$

Câu 9: Trong một chiếc hộp đựng 6 viên bi đỏ, 8 viên bi xanh, 10 viên bi trắng. Lấy ngẫu nhiên 4 viên bi. Tính số phần tử của biến cố: A: “ 4 viên bi lấy ra có đúng hai viên bi màu trắng”:

A.  $n\left(A\right)=4245$

B.   $n\left(A\right)=4295$

C.   $n\left(A\right)=4095$

D.  $n\left(A\right)=3095$

Hiển thị đáp án  

Đáp án: C

Giải thích:

Số cách chọn 4 viên bi có đúng hai viên bị màu trắng là: 

$C_{10}^2.C_{14}^2=4095$

Suy ra: $n\left(A\right)=4095$.

Câu 10: Gieo một đồng tiền và một con súcsắc. Số phần tử của không gian mẫu là:

A. 24

B. 12

C. 6

D. 8

Hiển thị đáp án  

Đáp án: B

Giải thích:

Mô tả không gian mẫu ta có:

$\Omega =\left\{\begin{array}{l}S1;S2;S3;S4;S5;S6;\\ N1;N2;N3;N4;N5;N6\end{array}\right\}$

Xem thêm các bài tổng hợp lý thuyết Toán lớp 11 đầy đủ, chi tiết khác:

Lý thuyết Xác suất của biến cố 

Lý thuyết Ôn tập chương 2

Lý thuyết Phương pháp quy nạp toán học 

Lý thuyết Dãy số

Lý thuyết Cấp số cộng