Lý thuyết Đại cương về đường thẳng và mặt phẳng (mới 2023 + Bài Tập) - Toán 11
Lý thuyết Đại cương về đường thẳng và mặt phẳng lớp 11 gồm lý thuyết chi tiết, ngắn gọn và bài tập tự luyện có lời giải chi tiết sẽ giúp học sinh nắm vững kiến thức trọng tâm Toán 11 Bài 1: Đại cương về đường thẳng và mặt phẳng.
Lý thuyết Toán 11 Bài 1: Đại cương về đường thẳng và mặt phẳng
Bài giảng Toán 11 Bài 1: Đại cương về đường thẳng và mặt phẳng (T1)
Bài giảng Toán 11 Bài 1: Đại cương về đường thẳng và mặt phẳng (T2)
A. Lý thuyết
I. Khái niệm mở đầu.
1. Mặt phẳng
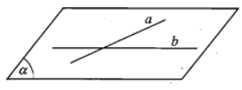
- Để biểu diễn mặt phẳng ta thường dùng hình bình hành hay một miền góc và ghi tên của mặt phẳng vào một góc của hình biểu diễn.

- Để kí hiệu mặt phẳng, ta thường dùng các chữ cái in hoa hoặc chữ cái Hi Lạp đặt trong dấu ngoặc ( ). Ví dụ: mp(P), mp(Q), mp(α), mp(β)…
2. Điểm thuộc mặt phẳng.
Cho điểm A và mặt phẳng (α).
- Khi điểm A thuộc mặt phẳng (α) ta nói A nằm trên (α) hay (α) chứa A, hay (α) đi qua A và kí hiệu là .
- Khi điểm A không thuộc mặt phẳng (α) ta nói điểm A nằm ngoài (α) hay (α) không chứa A và kí hiệu là .
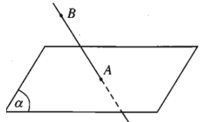
Hình trên cho ta hình biểu diễn của điểm A thuộc mặt phẳng , còn điểm B không thuộc (α).
3. Hình biểu diễn của một hình trong không gian
Để nghiên cứu hình học không gian người ta thường vẽ các hình không gian lên bảng, lên giấy. Ta gọi hình vẽ đó là hình biểu diễn của một hình không gian.
- Dưới đây là một vài hình biểu diễn của hình hộp chữ nhật.
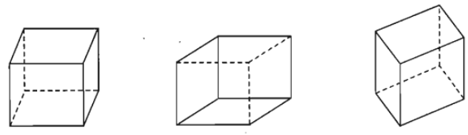
Để vẽ hình biểu diễn của một hình trong không gian người ta dựa vào những quy tắc sau đây:
- Hình biểu diễn của đường thẳng là đường thẳng, của đoạn thẳng là đoạn thẳng.
- Hình biểu diễn của hai đường thẳng song song là hai đường thẳng song song, của hai đường thẳng cắt nhau là hai đường thẳng cắt nhau.
- Hình biểu diễn phải giữ nguyên quan hệ thuộc giữa điểm và đường thẳng.
- Dùng nét liền để biểu diễn cho đường nhìn thấy và nét đứt đoạn biểu diễn cho đường bị che khuất.
II. Các tính chất thừa nhận
- Tính chất 1. Có một và chỉ một đường thẳng đi qua hai điểm phân biệt
- Tính chất 2. Có một và chỉ một mặt phẳng đi qua ba điểm không thẳng hàng.
Một mặt phẳng hoàn toàn xác định nếu biết nó đi qua ba điểm không thẳng hàng. Ta kí hiệu mặt phẳng đi qua ba điểm không thẳng hàng A, B, C là mặt phẳng (ABC) hoặc mp(ABC) hoặc (ABC).
- Tính chất 3. Nếu một đường thẳng có hai điểm phân biệt thuộc một mặt phẳng thì mọi điểm của đường thẳng đều thuộc mặt phẳng đó.
Nếu mọi điểm của đường thẳng d đều thuộc mặt phẳng (α) thì ta nói đường thẳng d nằm trong (α) hay (α) chứa d và kí hiệu là hay .
- Tính chất 4. Tồn tại bốn điểm không cùng thuộc một mặt phẳng.
Nếu có nhiều điểm cùng thuộc một mặt phẳng thì ta nói những điểm đó đồng phẳng, còn nếu không có mặt phẳng nào chứa các điểm đó thì ta nói chúng không đồng phẳng.
- Tính chất 5. Nếu hai mặt phẳng phân biệt có một điểm chung thì chúng còn có một điểm chung khác nữa.
Từ đó suy ra: Nếu hai mặt phẳng phân biệt có một điểm chung thì chúng sẽ có một đường thẳng chung đi qua điểm chung ấy.
Đường thẳng chung d của hai mặt phẳng phân biệt (α) và (β) được gọi là giao tuyến của (α) và (β) và kí hiệu là .
- Tính chất 6. Trên mỗi mặt phẳng, các kết quả đã biết trong hình học phẳng đều đúng.
III. Cách xác định mặt phẳng
1) Mặt phẳng được hoàn toàn xác định khi biết nó đi qua ba điểm không thẳng hàng.
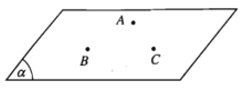
2) Mặt phẳng được hoàn toàn xác định khi biết nó đi qua một điểm và chứa một đường thẳng không đi qua điểm đó.
Cho đường thẳng d và điểm A không thuộc d. Khi đó điểm A và đường thẳng d xác định một mặt phẳng, kí hiệu là mp(A, d) hay (A, d) hoặc mp(d, A) hay (d, A).
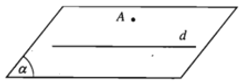
3) Mặt phẳng được hoàn toàn xác định khi biết nó chứa hai đường thẳng cắt nhau.
Cho hai đường thẳng cắt nhau a và b. Khi đó hai đường thẳng a và b xác định một mặt phẳng và kí hiệu là mp(a, b) hay (a, b) hoặc mp(b, a) hay (b, a).
IV. Hình chóp và hình tứ diện
1. Hình chóp
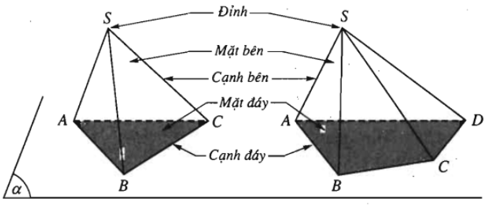
Trong mp(α) cho đa giác lồi A1A2…An. Lấy điểm S nằm ngoài (α). Lần lượt nối S với các đỉnh A1, A2,..,An ta được n tam giác SA1A2, SA2A3,…, SAnA1.
Hình gồm đa giác A1A2…An và n tam giác SA1A2, SA2A3,…, SAnA1 gọi là hình chóp, kí hiệu là S.A1A2…An.
Ta gọi S là đỉnh và đa giác A1A2…An là mặt đáy. Các tam giác SA1A2, SA2A3,…, SAnA1 gọi là các mặt bên, các đoạn SA1, SA2, …, SAn là các cạnh bên; các cạnh của đa giác đáy gọi là các cạnh đáy của hình chóp.
Ta gọi hình chóp có đáy là tam giác, tứ giác, ngũ giác,.. lần lượt là hình chóp tam giác, hình chóp tứ giác, hình chóp ngũ giác…
2. Hình tứ diện
Cho bốn điểm A, B, C, D không đồng phẳng. Hình gồm bốn tam giác ABC, ACD, ABD và BCD gọi là hình tứ diện (hay tứ diện) và được kí hiệu là ABCD.
Các điểm A, B, C, D gọi là các đỉnh của tứ diện.
Các đoạn thẳng AB, BC, CD, DA, CA, BD gọi là các cạnh của tứ diện.
Hai cạnh không đi qua một đỉnh gọi là hai cạnh đối diện.
Các tam giác ABC, ACD, ABD, BCD gọi là các mặt của tứ diện. Đỉnh không nằm trên một mặt gọi là đỉnh đối diện với mặt đó.
Hình tứ diện có 4 mặt là các tam giác đều gọi là hình tứ diện đều.
- Chú ý. Khi nói đến tam giác ta có thể hiểu là tập hợp các điểm thuộc các cạnh hoặc cũng có thể hiểu là tập hợp các điểm thuộc các cạnh và các điểm trong của tam giác đó. Tương tự có thể hiểu như vậy đối với đa giác.
3. Một số ví dụ
Ví dụ 1.Cho hình chóp S.ABCD có đáy là hình thang ABCD (AB // CD).
Tìm giao tuyến của hai mặt phẳng:
a) (SAC) và (SBD).
b) (SAD) và (SBC).
Lời giải:
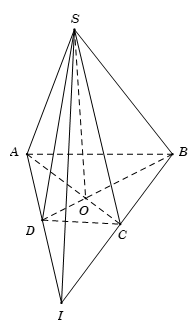
a) Trong mp(ABCD), gọi O là giao điểm của AC và BD.
Ta có S là điểm chung thứ nhất của hai mặt phẳng (SAC) và (SBD).
Lại có:
Suy ra, O là điểm chung thứ hai của hai mặt phẳng (SAC) và (SBD).
Vậy giao tuyến của hai mặt phẳng (SAC) và (SBD) là SO.
b) Trong mp(ABCD), gọi I là giao điểm của AD và BC.
Ta có S là điểm chung thứ nhất của hai mặt phẳng (SAD) và (SBC).
Lại có:
Suy ra, I là điểm chung thứ hai của hai mặt phẳng (SAD) và (SBC).
Vậy giao tuyến của hai mặt phẳng (SAD) và (SBC) là SI.
Ví dụ 2. Cho tứ diện ABCD. Gọi E và F lần lượt là trung điểm của AB và CD; G là trọng tâm tam giác BCD. Giao điểm của đường thẳng EG và mặt phẳng (ACD)?
Lời giải:
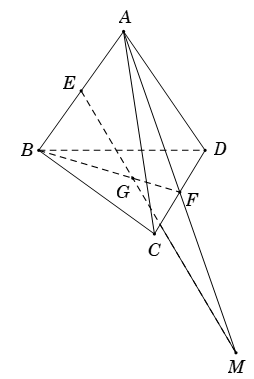
Vì G là trọng tâm tam giác BCD, F là trung điểm của CD nên
Ta có E là trung điểm của AB nên .
Chọn mp phụ chứa EG là (ABF)
+ Tìm giao tuyến của mp(ABF) và mp(ACD) ta có:
A là điểm chung thứ nhất.
Suy ra F là điểm chung thứ hai .
Do đó, giao tuyến của mp(ABF) và mp(ACD) là AF.
Trong mp(ABF), kéo dài AF cắt EG tại M. Khi đó, M là giao điểm của EG và mp(ACD).
B. Bài tập tự luyện
Bài 1. Cho bốn điểm A, B, C, D không cùng thuộc một mặt phẳng. Trên các đoạn thẳng AB, AC, BD lần lượt lấy các điểm M, N, P sao cho MN không song song với BC. Tìm giao tuyến của (BCD) và (MNP).
Lời giải:
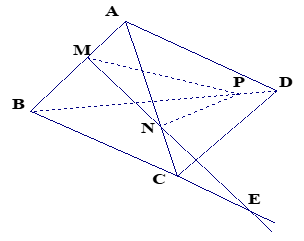
- Ta có:
mà
Suy ra, P là điểm chung của mp(BCD) và mp(MNP). (1)
- Trong mp (ABC), gọi E là giao điểm MN và BC
mà
mà
Suy ra, E là điểm chung của mp(BCD) và mp(MNP). (2)
- Từ (1), (2) suy ra PE là giao tuyến của mp(BCD) và mp(MNP).
Bài 2. Trong mp(a) cho tam giác ABC. Một điểm S không thuộc (a). Trên cạnh AB lấy một điểm P và rên các đoạn thẳng SA, SB ta lấy lần lượt hai điểm M, N sao cho MN không song song với AB.
Tìm giao điểm của đường thẳng MN với mặt phẳng (SPC).
Lời giải:
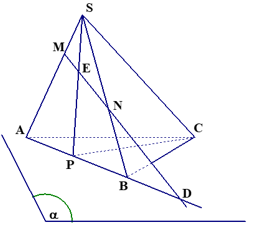
Cách 1: Trong (SAB) , gọi E = SP MN ta có:
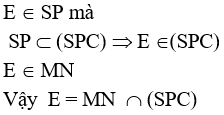
Cách 2: Chọn mp phụ chứa MN là mp(SAB).
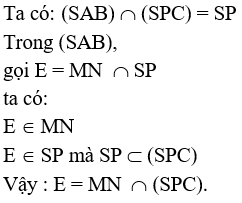
Bài 3. Cho tứ diện SABC. Trên SA, SB và SC lấy các điểm D, E và F sao cho DE
cắt AB tại I, EF cắt BC tại J, FD cắt CA tại K. Chứng minh ba điểm I, J, K thẳng
hàng.
Lời giải:
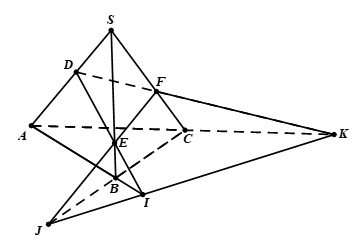
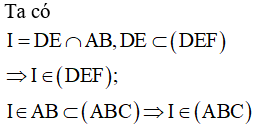
Suy ra, I thuộc giao tuyến của hai mp(DEF) và (ABC). (1)
Tương tự :
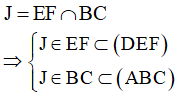
Suy ra, J thuộc giao tuyến của hai mp(DEF) và (ABC). (2)
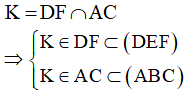
Suy ra, K thuộc giao tuyến của hai mp(DEF) và (ABC). (3)
Từ (1),(2) và (3) ta có I, J, K là điểm chung của hai mặt phẳng (DEF) và (ABC) nên chúng thẳng hàng.
Trắc nghiệm Toán 11 Bài 1: Đại cương về đường thẳng và mặt phẳng
Câu 1. Trong các khẳng định sau, khẳng định nào đúng?
A. Qua 2 điểm phân biệt có duy nhất một mặt phẳng
B. Qua 3 điểm phân biệt bất kì có duy nhất một mặt phẳng
C. Qua 3 điểm không thẳng hàng có duy nhất một mặt phẳng
D. Qua 4 điểm phân biệt bất kì có duy nhất một mặt phẳng
Đáp án: C
Giải thích:
+ A sai. Qua 2 điểm phân biệt, tạo được 1 đường thẳng, khi đó chưa đủ điều kiện để lập một mặt phẳng xác định. Có vô số mặt phẳng đi qua 2 điểm đã cho.
+ B sai. Trong trường hợp 3 điểm phân biệt thẳng hàng thì chỉ tạo được đường thẳng, khi đó có vô số mặt phẳng đi qua 3 điểm phân biệt thẳng hàng.
+ D sai. Trong trường hợp 4 điểm phân biệt thẳng hàng thì có vô số mặt phẳng đi qua 4 điểm đó hoặc trong trường hợp 4 điểm mặt phẳng không đồng phẳng thì sẽ tạo không tạo được mặt phẳng nào đi qua cả 4 điểm.
Câu 2. Trong không gian, cho 4 điểm không đồng phẳng. Có thể xác định được bao nhiêu mặt phẳng phân biệt từ các điểm đã cho?
A. 6
B. 4
C. 3
D. 2
Đáp án: B
Giải thích:
Với 3 điểm phân biệt không thẳng hàng, ta luôn tạo được 1 mặt phẳng xác định.
Khi đó, với 4 điểm không đồng phẳng ta tạo được tối đa mặt phẳng.
Câu 3. Cho tứ diện ABCD. Gọi E, F, G là các điểm lần lượt thuộc các cạnh AB, AC, BD sao cho EF cắt BC tại I, EG cắt AD tại H. Ba đường thẳng nào sau đây đồng quy?
A.
B.
C. .
D.
Đáp án: B
Giải thích:
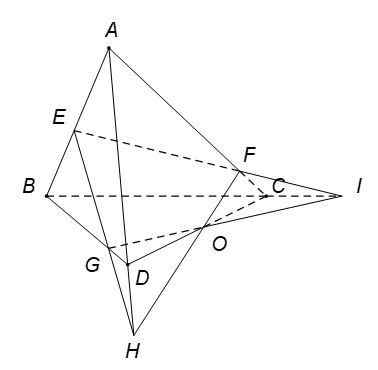
Phương pháp: Để chứng minh ba đường thẳng đồng quy ta chứng minh giao điểm của hai đường thẳng và là điểm chung của hai mặt phẳng và ; đồng thời là giao tuyến và .
Gọi . Ta có
● mà suy ra .
● mà suy ra .
Do đó .
Mà .
Từ và , suy ra .
Vậy ba đường thẳng đồng quy.
Câu 4. Cho hình chóp có đáy không phải là hình thang. Trên cạnh SC lấy điểm M. Gọi N là giao điểm của đường thẳng SD với mặt phẳng . Mệnh đề nào sau đây đúng?
A. Ba đường thẳng đôi một song song.
B. Ba đường thẳng đôi một cắt nhau.
C. Ba đường thẳng đồng quy.
D. Ba đường thẳng cùng thuộc một mặt phẳng.
Đáp án: C
Giải thích:
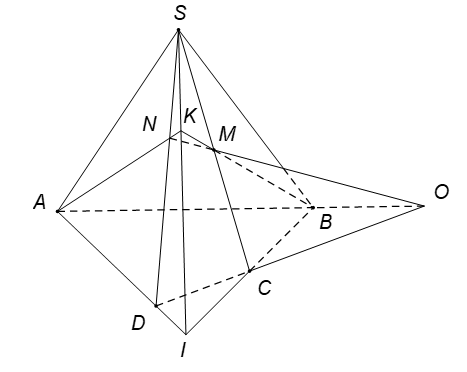
Gọi Trong mặt phẳng , gọi . Trong mặt phẳng , gọi .
Khi đó N là giao điểm của đường thẳng SD với mặt phẳng .
Gọi . Ta có:
● mà suy ra .
● mà suy ra .
Do đó .
Mà .
Từ và , suy ra . Vậy ba đường thẳng đồng quy tại O.
Câu 5. Các yếu tố nào sau đây xác định một mặt phẳng duy nhất?
A. Ba điểm phân biệt
B. Một điểm và một đường thẳng
C. Hai đường thẳng cắt nhau
D. Bốn điểm phân biệt
Đáp án: C
Giải thích:
+ A sai. Trong trường hợp 3 điểm phân biệt thẳng hàng thì sẽ có vô số mặt phẳng chứa 3 điểm thẳng hàng đã cho.
+ B sai. Trong trường hợp điểm thuộc đường thẳng đã cho, khi đó ta chỉ có 1 đường thẳng, có vô số mặt phẳng đi qua đường thẳng đó.
+ D sai. Trong trường hợp 4 điểm phân biệt thẳng hàng thì có vô số mặt phẳng đi qua 4 điểm đó hoặc trong trường hợp 4 điểm mặt phẳng không đồng phẳng thì sẽ tạo không tạo được mặt phẳng nào đi qua cả 4 điểm.
Câu 6. Cho tứ diện . Gọi lần lượt là các điểm trên các cạnh và AC sao cho LM không song song với AB, LN không song song với SC. Mặt phẳng cắt các cạnh lần lượt tại . Ba điểm nào sau đây thẳng hàng?
A.
B.
C.
D.
Đáp án: B
Giải thích:
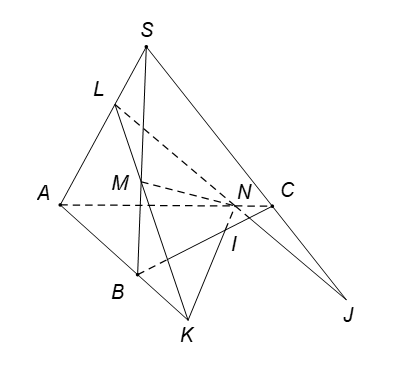
Ta có
● suy M là điểm chung của và .
● I là điểm chung của và .
● J là điểm chung của và .
Vậy M , J , I thẳng hàng vì cùng thuộc giao tuyến của và .
Câu 7. Cho tứ diện ABCD. Gọi G là trọng tâm tam giác BCD, M là trung điểm CD, I là điểm ở trên đoạn thẳng AG, BI cắt mặt phẳng tại J. Khẳng định nào sau đây sai?
A.
B. thẳng hàng.
C. J là trung điểm của AM.
D.
Đáp án: C
Giải thích:
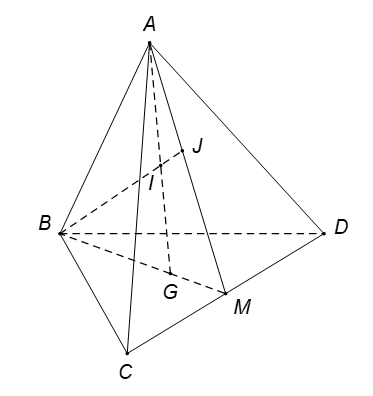
Ta có A là điểm chung thứ nhất giữa hai mặt phẳng và
Do
là điểm chung thứ hai giữa hai mặt phẳng và
A đúng.
Ta có
đồng phẳng.
thẳng hàng
B đúng.
Ta có
D đúng.
Điểm I di động trên AG nên J có thể không phải là trung điểm của AM
C sai.
Câu 8. Trong các mệnh đề sau đây, mệnh đề nào sai?
A. Hai mặt phẳng có một điểm chung thì chúng có vô số điểm chung khác nữa
B. Hai mặt phẳng có một điểm chung thì chúng có một đường thẳng chung duy nhất
C. Hai mặt phẳng phân biệt có một điểm chung thì chúng có một đường thẳng chung duy nhất
D. Hai mặt phẳng cùng đi qua 3 điểm A , B , C không thẳng hàng thì hai mặt phẳng đó trùng nhau
Đáp án: B
Giải thích:
Nếu 2 mặt phẳng trùng nhau, khi đó 2 mặt phẳng có vô số điểm chung và chung nhau vô số đường thẳng.
Câu 9. Cho 3 đường thẳng không cùng thuộc một mặt phẳng và cắt nhau từng đôi. Khẳng định nào sau đây đúng?
A. 3 đường thẳng trên đồng quy
B. 3 đường thẳng trên trùng nhau
C. 3 đường thẳng trên chứa 3 cạnh của một tam giác
D. Các khẳng định ở A, B, C đều sai
Đáp án: A
Giải thích:
+ B sai. Nếu 3 đường thẳng trùng nhau thì chúng sẽ cùng thuộc 1 mặt phẳng.
+ C sai. Nếu 3 đường thẳng trên chứa 3 cạnh của một tam giác khi đó sẽ tạo được 3 điểm phân biệt không thẳng hàng (là 3 đỉnh của tam giác), chúng lập thành 1 mặt phẳng xác định, 3 đường thẳng sẽ cùng thuộc 1 mặt phẳng.
Câu 10. Thiết diện của 1 tứ diện có thể là:
A. Tam giác
B. Tứ giác
C. Ngũ giác
D. Tam giác hoặc tứ giác
Đáp án: D
Giải thích:
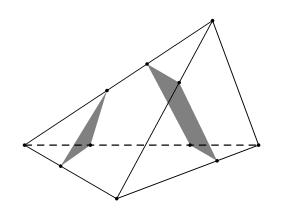
Khi thiết diện cắt 3 mặt của tứ diện thì sẽ tạo thành 3 giao tuyến. Ba giao tuyến lập thành 1 hình tam giác.
Khi thiết diện cắt cả 4 mặt của tứ diện thì sẽ tạo thành 4 giao tuyến. Bốn giao tuyến lập thành 1 hình tứ giác.
Thiết diện không thể là ngũ giác vì thiết diện có 4 mặt, số giao tuyến tối đa là 4.
Xem thêm các bài tổng hợp lý thuyết Toán lớp 11 đầy đủ, chi tiết khác:
Lý thuyết Hai đường thẳng chéo nhau và hai đường thẳng song song
Lý thuyết Đường thẳng và mặt phẳng song song
Lý thuyết Hai mặt phẳng song song
Lý thuyết Phép chiếu song song. Hình biểu diễn của một hình không gian
Xem thêm các chương trình khác:
- Giải sgk Hóa học 11 | Giải bài tập Hóa học 11 Học kì 1, Học kì 2 (Sách mới)
- Lý thuyết Hóa học 11(sách mới) | Kiến thức trọng tâm Hóa 11
- Giải sbt Hóa học 11 (sách mới) | Sách bài tập Hóa học 11
- Các dạng bài tập Hóa học lớp 11
- Giáo án Hóa học lớp 11 mới nhất
- Tóm tắt tác phẩm Ngữ văn 11 (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Soạn văn 11 (hay nhất) | Để học tốt Ngữ Văn 11 (sách mới)
- Soạn văn 11 (ngắn nhất) | Để học tốt Ngữ văn 11 (sách mới)
- Tác giả tác phẩm Ngữ văn 11 (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Văn mẫu 11 (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Giải sgk Tiếng Anh 11 (thí điểm)
- Giải sgk Tiếng Anh 11 | Giải bài tập Tiếng anh 11 Học kì 1, Học kì 2 (sách mới)
- Giải sbt Tiếng Anh 11 (sách mới) | Sách bài tập Tiếng Anh 11
- Giải sbt Tiếng Anh 11 (thí điểm)
- Giải sgk Lịch sử 11 | Giải bài tập Lịch sử 11 Học kì 1, Học kì 2 (sách mới)
- Lý thuyết Lịch Sử 11(sách mới) | Kiến thức trọng tâm Lịch Sử 11
- Giải Tập bản đồ Lịch sử 11
- Giải sgk Vật Lí 11 | Giải bài tập Vật lí 11 Học kì 1, Học kì 2 (sách mới)
- Giải sbt Vật Lí 11 (sách mới) | Sách bài tập Vật Lí 11
- Lý thuyết Vật Lí 11 (sách mới) | Kiến thức trọng tâm Vật Lí 11
- Các dạng bài tập Vật Lí lớp 11
- Giáo án Vật lí lớp 11 mới nhất
- Giải sgk Sinh học 11 | Giải bài tập Sinh học 11 Học kì 1, Học kì 2 (sách mới)
- Lý thuyết Sinh học 11 (sách mới) | Kiến thức trọng tâm Sinh 11
- Giải sgk Giáo dục công dân 11
- Lý thuyết Giáo dục công dân 11
- Lý thuyết Địa Lí 11 (sách mới) | Kiến thức trọng tâm Địa lí 11
- Giải Tập bản đồ Địa Lí 11
- Giải sgk Giáo dục quốc phòng - an ninh 11
