Lý thuyết Định nghĩa và ý nghĩa của đạo hàm (mới 2023 + Bài Tập) - Toán 11

Lý thuyết Toán 11 Bài 1: Định nghĩa và ý nghĩa của đạo hàm

Bài giảng Toán 11 Bài 1: Định nghĩa và ý nghĩa của đạo hàm

A. LÝ THUYẾT

I. Đạo hàm tại một điểm

1. Định nghĩa đạo hàm tại một điểm

 Cho hàm số y = f(x) xác định trên khoảng (a; b) và x₀ thuộc (a; b). Nếu tồn tại giới hạn (hữu hạn): $\underset{\mathrm{x}\to {\mathrm{x}}_0}{\lim }\frac{\mathrm{f}\left(\mathrm{x}\right)-\mathrm{f}\left({\mathrm{x}}_0\right)}{\mathrm{x}-{\mathrm{x}}_0}$ thì giới hạn đó được gọi là đạo hàm của hàm số y = f(x) tại điểm x₀ và được kí hiệu là f^'(x₀). Vậy $\boxed{\mathrm{f}\text{'}\left({\mathrm{x}}_0\right)=\underset{\mathrm{x}\to {\mathrm{x}}_0}{\lim }\frac{\mathrm{f}\left(\mathrm{x}\right)-\mathrm{f}\left({\mathrm{x}}_0\right)}{\mathrm{x}-{\mathrm{x}}_0}.}$

* Chú ý:

Đại lượng ∆x = x- x₀ được gọi là số gia của đối số tại x₀.

Đại lượng ∆y= f(x) – f(x₀)= f(x₀ + ∆x) –  f(x₀) được gọi là số gia tương ứng của hàm số. Như vậy: $\mathrm{y}\text{'}\left({\mathrm{x}}_0\right)=\underset{\mathrm{\Delta x}\to \infty }{\lim }\frac{\mathrm{\Delta y}}{\mathrm{\Delta x}}$. 

2. Quy tắc tính đạo hàm bằng định nghĩa:

Để tính đạo hàm của hàm số y = f(x) tại điểm x₀ bằng định nghĩa, ta có quy tắc sau đây:

+ Bước 1: Giả sử ∆x là số gia của đối số tại x₀ tính:

∆y= f(x₀ + ∆x) – f( x₀) .

+ Bước 2: Lập tỉ số $\frac{\mathrm{\Delta y}}{\mathrm{\Delta x}}.$.

+ Bước 3: Tìm $\underset{\mathrm{\Delta x}\to 0}{\lim }\frac{\mathrm{\Delta y}}{\mathrm{\Delta x}}.$

Ví dụ 1. Cho hàm số $\mathrm{y}=\sqrt{2\mathrm{x}-3}$, có $\mathrm{\Delta x}$ là số gia của đối số tại x = 2. Khi đó $\frac{\mathrm{\Delta y}}{\mathrm{\Delta x}}$ bằng bao nhiêu.

Lời giải

Tập xác định của hàm số đã cho là: $\mathrm{D}=\left[\frac{3}{2};+\infty \right)$.

Giả sử ∆x là số gia của đối số tại x₀ = 2. Ta có: $\mathrm{\Delta y}=\mathrm{f}\left(2+\mathrm{\Delta x}\right)-\mathrm{f}\left(2\right)=\sqrt{2.\left(2+\mathrm{\Delta x}\right)-3}$ $-\sqrt{2.2-3}=\sqrt{2\mathrm{\Delta x}+1}-1$

Khi đó:

$$\begin{gathered} \frac{\mathrm{\Delta y}}{\mathrm{\Delta x}}=\frac{\sqrt{2\mathrm{\Delta x}+1}-1}{\mathrm{\Delta x}} \\ \Rightarrow \underset{\mathrm{\Delta x}\to 0}{\lim }\frac{\mathrm{\Delta y}}{\mathrm{\Delta x}}=\underset{\mathrm{\Delta x}\to 0}{\lim }\frac{\sqrt{2\mathrm{\Delta x}+1}-1}{\mathrm{\Delta x}}= \\ \underset{\mathrm{\Delta x}\to 0}{\lim }\frac{\left(\sqrt{2\mathrm{\Delta x}+1}-1\right).\left(\sqrt{2\mathrm{\Delta x}+1}+1\right)}{\mathrm{\Delta x}.\left(\sqrt{2\mathrm{\Delta x}+1}+1\right)} \\ =\underset{\mathrm{\Delta x}\to 0}{\lim }\frac{2\mathrm{\Delta x}}{\mathrm{\Delta x}.\left(\sqrt{2\mathrm{\Delta x}+1}+1\right)} \\ =\underset{\mathrm{\Delta x}\to 0}{\lim }\frac{2}{\sqrt{2\mathrm{\Delta x}+1}+1}=1 \end{gathered}$$

Vậy f’(2) = 1.

3. Quan hệ giữa sự tồn tại của đạo hàm và tính liên tục của hàm số

Định lý 1. Nếu hàm số y= f( x) có đạo hàm tại x0 thì nó liên tục tại điểm đó.

Chú ý:

+ Nếu hàm số y= f(x) gián đoạn tại x0 thì hàm số không có đạo hàm tại điểm đó.

+ Một hàm số liên tục tại một điểm có thể không có đạo hàm tại điểm đó.

Ví dụ 2. Chẳng hạn hàm số $\mathrm{y}=\mathrm{f}\left(\mathrm{x}\right)=\left\{\begin{array}{l}-{\mathrm{x}}^2\mathrm{khi}\mathrm{x}\ge 0\\ \mathrm{x}\mathrm{khi}\mathrm{x}<0\end{array}\right.$ liên tục tại x = 0 nhưng không có đạo hàm tại đó. Ta nhận xét rằng đồ thị của hàm số này là một đường liền, nhưng bị gãy tại điểm O(0;0) như hình vẽ sau:

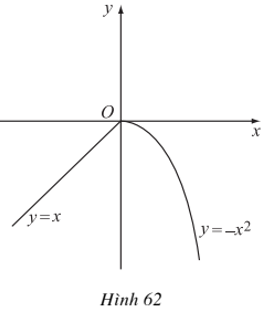
4. Ý nghĩa của đạo hàm

a) Ý nghĩa hình học của đạo hàm:

+) Định lí: Đạo hàm của hàm số y= f(x) tại điểm x = x₀ là hệ số góc của tiếp tuyến M₀T của đồ thị hàm số y= f( x) tại điểm M₀(x₀; f(x₀)).

+) Định lí: Phương trình tiếp tuyến của đồ thị hàm số y = f(x) tại điểm M₀(x₀; f(x₀)) là:

y – y₀= f’(x₀) ( x- x₀) trong đó y₀= f(x₀).

Ví dụ 3. Viết phương trình tiếp tuyến của đường cong y = x³ – 3x² + 2 tại điểm có hoành độ x = 3.

Lời giải

Bằng định nghĩa ta tính được: y’(3) = 9.

Do đó hệ số góc của tiếp tuyến là 9.

Ta có: y(3) = 2.

Vậy phương trình tiếp tuyến của đường cong tại điểm có hoành độ x = 3 là:

y = 9(x – 3) + 2 = 9x – 27 + 2 = 9x – 25.

b) Ý nghĩa vật lý của đạo hàm:

+) Vận tốc tức thời:

Xét chuyển động thẳng xác định bởi phương trình: s= s(t); với s= s(t) là một hàm số có đạo hàm. Vận tốc tức thời tại thời điểm t0 là đạo hàm của hàm số s= s(t) tại t₀: v(t₀) = s’(t₀).

+) Cường độ tức thời:

Nếu điện lượng Q truyền trong dây dẫn là một hàm số của thời gian: Q= Q(t) ( là hàm số có đạo hàm) thì cường độ tức thời của dòng điện tại thời điểm t0 là đạo hàm của hàm số Q= Q(t) tại t₀: I(t₀) = Q’(t₀) .

Ví dụ 4. Một xe máy chuyển động theo phương trình : s(t)= t² + 6t+ 10 trong đó t đơn vị là giây; s là quãng đường đi được đơn vị m. Tính vận tốc tức thời của xe tại thời điểm t= 3.

Lời giải

Phương trình vận tốc của xe là v( t)=s' ( t)=2t+6 ( m/s)

⇒ Vận tốc tức thời của xe tại thời điểm t= 3 là:

V(3)= 2.3+ 6 = 12 (m/s)

Chọn A.

II. Đạo hàm trên một khoảng

Hàm số y = f(x) được gọi là có đạo hàm trên khoảng (a; b) nếu nó có đạo hàm tại mọi điểm x trên khoảng đó.

Khi đó ta gọi hàm số f’:

 $$\begin{gathered} \left(\mathrm{a};\mathrm{b}\right)\to \mathrm{ℝ} \\ \mathrm{x}\mapsto \mathrm{f}\text{'}\left(\mathrm{x}\right) \end{gathered}$$

là đạo hàm của hàm số y = f(x) trên khoảng (a;b), kí hiệu là y’ hay f’(x).

Ví dụ 5. Hàm số y = x² – 2x có đạo hàm y’ = 2x – 2 trên khoảng $\left(-\infty ;+\infty \right)$.

Hàm số $\mathrm{y}=\frac{2}{\mathrm{x}}$ có đạo hàm $\mathrm{y}\text{'}=-\frac{2}{{\mathrm{x}}^2}$ trên các khoảng $\left(-\infty ;0\right)$ và $\left(0;+\infty \right)$.

B. BÀI TẬP

Bài 1. Cho hàm số: $\mathrm{y}=\mathrm{f}\left(\mathrm{x}\right)=\frac{{\mathrm{x}}^2+\mathrm{x}}{\mathrm{x}-2}$ (C)

a) Hãy tính đạo hàm bằng định nghĩa của hàm số đã cho tại x = 1.

b) Viết phương trình tiếp tuyến của hàm số (C) tại điểm A(1;-2).

Lời giải

a) Tập xác định của hàm số đã cho là: $\mathrm{D}=\mathrm{ℝ}\backslash \left\{2\right\}$.

Giả sử ∆x là số gia của đối số tại x₀ = 1. Ta có:

$$\begin{gathered} \mathrm{\Delta y}=\mathrm{f}\left(1+\mathrm{\Delta x}\right)-\mathrm{f}\left(1\right) \\ =\frac{{\left(1+\mathrm{\Delta x}\right)}^2+1+\mathrm{\Delta x}}{1+\mathrm{\Delta x}-2}-\frac{1^2+1}{1-2} \\ =\frac{{\left(\mathrm{\Delta x}\right)}^2+2\mathrm{\Delta x}+1+1+\mathrm{\Delta x}}{\mathrm{\Delta x}-1}+2 \\ =\frac{{\left(\mathrm{\Delta x}\right)}^2+3\mathrm{\Delta x}+2}{\mathrm{\Delta x}-1}+2 \\ =\frac{{\left(\mathrm{\Delta x}\right)}^2+3\mathrm{\Delta x}+2}{\mathrm{\Delta x}-1}+\frac{2\mathrm{\Delta x}-2}{\mathrm{\Delta x}-1} \\ =\frac{{\left(\mathrm{\Delta x}\right)}^2+5\mathrm{\Delta x}}{\mathrm{\Delta x}-1} \end{gathered}$$

Khi đó:

$$\begin{gathered} \frac{\mathrm{\Delta y}}{\mathrm{\Delta x}}=\frac{\frac{{\left(\mathrm{\Delta x}\right)}^2+5\mathrm{\Delta x}}{\mathrm{\Delta x}-1}}{\mathrm{\Delta x}}=\frac{\frac{\mathrm{\Delta x}\left(\mathrm{\Delta x}+5\right)}{\mathrm{\Delta x}-1}}{\mathrm{\Delta x}}=\frac{\mathrm{\Delta x}+5}{\mathrm{\Delta x}-1} \\ \Rightarrow \underset{\mathrm{\Delta x}\to 0}{\lim }\frac{\mathrm{\Delta y}}{\mathrm{\Delta x}}=\underset{\mathrm{\Delta x}\to 0}{\lim }\frac{\mathrm{\Delta x}+5}{\mathrm{\Delta x}-1}=-5. \end{gathered}$$

Vậy f’(1) = - 5.

b) Bằng định nghĩa ta tính được: y’(1) = -5.

Do đó hệ số góc của tiếp tuyến là -5.

Ta có: y(1) = - 2.

Vậy phương trình tiếp tuyến của đường cong tại điểm A(1;-2) là:

y = -5(x – 1) - 2 = -5x + 5 - 2 = -5x + 3.

Bài 2. Chứng minh rằng hàm số $\mathrm{f}\left(\mathrm{x}\right)=\left\{\begin{array}{l}{\left(\mathrm{x}-1\right)}^2\mathrm{khi}\mathrm{x}\ge 0\\ {\left(\mathrm{x}+1\right)}^2\mathrm{khi}\mathrm{x}<0\end{array}\right.$ không có đạo hàm tại x = 0 nhưng liên tục tại điểm đó.

Lời giải

Ta có f(0) = 1.

Trước hết, ta tính giới hạn bên phải của tỉ số $\frac{\mathrm{f}\left(\mathrm{x}\right)-\mathrm{f}\left(0\right)}{\mathrm{x}-0}$. Ta có:

$$\begin{gathered} \underset{\mathrm{x}\to 0^{+}}{\lim }\frac{\mathrm{f}\left(\mathrm{x}\right)-\mathrm{f}\left(0\right)}{\mathrm{x}-0} \\ =\underset{\mathrm{x}\to 0^{+}}{\lim }\frac{{\left(\mathrm{x}-1\right)}^2-1}{\mathrm{x}} \\ =\underset{\mathrm{x}\to 0^{+}}{\lim }\frac{\mathrm{x}\left(\mathrm{x}-2\right)}{\mathrm{x}}=\underset{\mathrm{x}\to 0^{+}}{\lim }\left(\mathrm{x}-2\right) \\ =-2. \left(\mathrm{x}\ne 0\right) \end{gathered}$$

Giới hạn bên trái của tỉ số $\frac{\mathrm{f}\left(\mathrm{x}\right)-\mathrm{f}\left(0\right)}{\mathrm{x}-0}$, ta có:

$$\begin{gathered} \underset{\mathrm{x}\to 0^{-}}{\lim }\frac{\mathrm{f}\left(\mathrm{x}\right)-\mathrm{f}\left(0\right)}{\mathrm{x}-0}=\underset{\mathrm{x}\to 0^{-}}{\lim }\frac{{\left(\mathrm{x}+1\right)}^2-1}{\mathrm{x}} \\ =\underset{\mathrm{x}\to 0^{-}}{\lim }\frac{\mathrm{x}\left(\mathrm{x}+2\right)}{\mathrm{x}}=\underset{\mathrm{x}\to 0^{-}}{\lim }\left(\mathrm{x}+2\right)=2. \end{gathered}$$

Vì giới hạn hai bên khác nhau nên không tồn tại $\underset{\mathrm{x}\to 0}{\lim }\frac{\mathrm{f}\left(\mathrm{x}\right)-\mathrm{f}\left(0\right)}{\mathrm{x}-0}$. Điều này chứng tỏ hàm số không có đạo hàm tại điểm x = 0.

Ta có:

$$\begin{gathered} \underset{\mathrm{x}\to 0^{+}}{\lim }\mathrm{f}\left(\mathrm{x}\right)=\underset{\mathrm{x}\to 0^{+}}{\lim }{\left(\mathrm{x}-1\right)}^2=1 \\ \underset{\mathrm{x}\to 0^{-}}{\lim }\mathrm{f}\left(\mathrm{x}\right)=\underset{\mathrm{x}\to 0^{-}}{\lim }{\left(\mathrm{x}+1\right)}^2=1 \\ \underset{\mathrm{x}\to 0^{-}}{\Rightarrow \lim }\mathrm{f}\left(\mathrm{x}\right)=\underset{\mathrm{x}\to 0^{+}}{\lim }{\left(\mathrm{x}+1\right)}^2=1 \end{gathered}$$

Do đó hàm số liên tục tại x = 1.

Vậy hàm số liên tục tại x = 1 nhưng không có đạo hàm tại x = 1.

Bài 3. Cho biết điện lượng truyền trong dây dẫn theo thời gian biểu thị bởi hàm số Q(t) = 2t² + t, trong đó t được tính bằng giây (s) và Q được tính theo Culong (C). Tính cường độ dòng điện tại thời điểm t = 4s.

Lời giải

Cường độ dòng điện tại t = 4 là: I(4) = Q’(4).

Đạo hàm của hàm Q(t) tại t = 4 bằng 17.

Vậy cường độ dòng điện tại t = 4 là 17 A.

Bài 4. Viết phương trình tiếp tuyến của đồ thị của các hàm số:

a) $\mathrm{y}=\sqrt{2\mathrm{x}+1}$, biết hệ số góc của tiếp tuyến là $\frac{1}{3}$;

b) y = x³ + 2x tại điểm có hoành độ bằng  2.

Lời giải

a)

$$\begin{gathered} \underset{\mathrm{x}\to {\mathrm{x}}_0}{\lim }\frac{\mathrm{f}\left(\mathrm{x}\right)-\mathrm{f}\left({\mathrm{x}}_0\right)}{\mathrm{x}-{\mathrm{x}}_0} \\ =\underset{\mathrm{x}\to {\mathrm{x}}_0}{\lim }\frac{\sqrt{2\mathrm{x}+1}-\sqrt{2{\mathrm{x}}_0+1}}{\mathrm{x}-{\mathrm{x}}_0} \\ =\underset{\mathrm{x}\to {\mathrm{x}}_0}{\lim }\frac{2\left(\mathrm{x}-{\mathrm{x}}_0\right)}{\left(\mathrm{x}-{\mathrm{x}}_0\right)\left(\sqrt{2\mathrm{x}+1}+\sqrt{2{\mathrm{x}}_0+1}\right)} \\ =\underset{\mathrm{x}\to {\mathrm{x}}_0}{\lim }\frac{2}{\sqrt{2\mathrm{x}+1}+\sqrt{2{\mathrm{x}}_0+1}}=\frac{1}{\sqrt{2{\mathrm{x}}_0+1}} \\ \Rightarrow \frac{1}{\sqrt{2{\mathrm{x}}_0+1}}=\frac{1}{3} \\ \iff \sqrt{2{\mathrm{x}}_0+1}=3 \\ \iff 2{\mathrm{x}}_0+1=9 \\ \iff {\mathrm{x}}_0=4\Rightarrow \mathrm{y}\left(4\right)=\sqrt{2.4+1}=3 \end{gathered}$$

Vậy phương trình tiếp tuyến của đồ thị của hàm số đã cho là:

$\mathrm{y}=\frac{1}{3}\left(\mathrm{x}-4\right)+3=\frac{1}{3}\mathrm{x}-\frac{4}{3}+3=\frac{1}{3}\mathrm{x}+\frac{5}{3}.$

b)

$$\begin{gathered} \underset{\mathrm{x}\to 2}{\lim }\frac{\mathrm{f}\left(\mathrm{x}\right)-\mathrm{f}\left(2\right)}{\mathrm{x}-2} \\ =\underset{\mathrm{x}\to 2}{\lim }\frac{{\mathrm{x}}^3+2\mathrm{x}-\left(2^3+2.2\right)}{\mathrm{x}-2} \\ =\underset{\mathrm{x}\to 2}{\lim }\frac{{\mathrm{x}}^3+2\mathrm{x}-12}{\mathrm{x}-2} \\ =\underset{\mathrm{x}\to 2}{\lim }\frac{\left(\mathrm{x}-2\right)\left({\mathrm{x}}^2+2\mathrm{x}+6\right)}{\mathrm{x}-2} \\ =\underset{\mathrm{x}\to 2}{\lim }\left({\mathrm{x}}^2+2\mathrm{x}+6\right)=14 \end{gathered}$$

Ta có y(2) = 12.

Phương trình tiếp tuyến của đồ thị hàm số đã cho là:

y = 14(x – 2) + 12 = 14x – 28 + 12 = 14x – 16.

Vậy phương trình tiếp tuyến của đồ thị hàm số đã cho là y = 14x – 16.

Trắc nghiệm Toán 11 Bài 1: Định nghĩa và ý nghĩa của đạo hàm

Câu 1: Cho hàm số $f\left(x\right)=\left\{\begin{array}{l}\sqrt{x}khix>1\\ x^{2}khix\le 1\end{array}\right.$ . Tính $f\text{'}\left(1\right)$ ?

A. $\frac{1}{2}$

B. 1

C. 2

D. không tồn tại.

Hiển thị đáp án  

Đáp án: D

Giải thích:

$\begin{array}{l}\underset{x\to 1+}{\lim }\frac{f\left(x\right)-f\left(1\right)}{x-1}\\ =\underset{x\to 1+}{\lim }\frac{\sqrt{x}-1}{x-1}\\ =\underset{x\to 1+}{\lim }\frac{1}{\sqrt{x}+1}=\frac{1}{2}\end{array}$

$\begin{array}{l}\underset{x\to 1-}{\lim }\frac{f\left(x\right)-f\left(1\right)}{x-1}\\ =\underset{x\to 1-}{\lim }\frac{x^2-1}{x-1}\\ =\underset{x\to 1-}{\lim }(x+1)=2\end{array}$

$\Rightarrow \underset{x\to 1+}{\lim }\frac{f\left(x\right)-f\left(1\right)}{x-1}\ne \underset{x\to 1-}{\lim }\frac{f\left(x\right)-f\left(1\right)}{x-1}$

Vậy không tồn tại đạo hàm của hàm số tại .

Câu 2: Cho hàm số $\left\{\begin{array}{l}2x+3 khi x\ge 1\\ \frac{x^3+2x^2-7x+4}{x-1} khi x<1\end{array}\right.$. Giá trị của $f\text{'}\left(1\right)$ bằng:

A. 0

B. 4

C. 5

D. không tồn tại

Hiển thị đáp án  

Đáp án: D

Giải thích:

Ta có: f(1) = 5

$\begin{array}{l}\underset{x\to 1+}{\lim }\frac{f\left(x\right)-f\left(1\right)}{x-1}\\ =\underset{x\to 1+}{\lim }\frac{2x+3-5}{x-1}\\ =\underset{x\to 1+}{\lim }\frac{2x-2}{x-1}=2\end{array}$

$\begin{array}{l}\underset{x\to 1-}{\lim }\frac{f\left(x\right)-f\left(1\right)}{x-1}\\ =\underset{x\to 1-}{\lim }\frac{\frac{x^3+2x^2-7x+4}{x-1}-5}{x-1}\end{array}$

$\begin{array}{l}=\underset{x\to 1-}{\lim }\frac{x^3+2x^2-12x+9}{{(x-1)}^2}\\ =\underset{x\to 1-}{\lim }\frac{(x-1)(x^2+3x-9)}{{(x-1)}^2}\end{array}$

$=\underset{x\to 1-}{\lim }\frac{x^2+3x-9}{x-1}=+\infty$

$\Rightarrow \underset{x\to 1+}{\lim }\frac{f\left(x\right)-f\left(1\right)}{x-1}\ne \underset{x\to 1-}{\lim }\frac{f\left(x\right)-f\left(1\right)}{x-1}$

Vậy hàm số không tồn tại đạo hàm tại .

Câu 3: Khi tính đạo hàm của hàm số $f\left(x\right)=x^2+5x-3$ tại điểm $x_0=2$, một học sinh đã tính theo các bước sau:

Bước 1: $f\left(x\right)-f\left(2\right)=f\left(x\right)-11$

Bước 2: $\begin{array}{l}\frac{f\left(x\right)-f\left(2\right)}{x-2}\\ =\frac{x^2+5x-3-11}{x-2}\\ =\frac{(x-2)(x+7)}{x-2}=x+7\end{array}$

Bước 3: $\begin{array}{l}\underset{x\to 2}{\lim }\frac{f\left(x\right)-f\left(2\right)}{x-2}\\ =\underset{x\to 2}{\lim }(x+7)=9\\ \Rightarrow f\text{'}\left(2\right)=9\end{array}$

Tính toán trên nếu sai thì sai ở bước nào?

A. Bước 1

B. Bước 2

C. Bước 3

D. Tính toán đúng

Hiển thị đáp án  

Đáp án: D

Giải thích:

Bài giải trên hoàn toàn đúng.

Câu 4: Cho hàm số $f\left(x\right)$ liên tục tại $x_0$. Đạo hàm của $f\left(x\right)$ tại $x_0$ là

A. $f\left(x_0\right)$ 

B. $\frac{f(x_0+h)-f\left(x_0\right)}{h}$

C. $\underset{h\to 0}{\lim }\frac{f(x_0+h)-f\left(x_0\right)}{h}$ (nếu tồn tại giới hạn).

D. $\underset{h\to 0}{\lim }\frac{f(x_0+h)-f(x_0-h)}{h}$ (nếu tồn tại giới hạn).

Hiển thị đáp án  

Đáp án: C

Giải thích:

Định nghĩa $f\text{'}\left(x_0\right)=\underset{\Delta x\to 0}{\lim }\frac{f(x_0+\Delta x)-f\left(x_0\right)}{\Delta x}$ hay $f\text{'}\left(x_0\right)=\frac{f(x_0+h)-f(x_0-h)}{h}$ (nếu tồn tại giới hạn).

Câu 5: Cho hàm số $f\left(x\right)=\sqrt{x+1}$. Tính đạo hàm của hàm số tại điểm $x_0=1$ 

A. $\frac{\sqrt{2}}{4}$

B. $\frac{\sqrt{2}}{2}$

C. $2\sqrt{2}$

D. $\frac{\sqrt{2}}{3}$

Hiển thị đáp án  

Đáp án: A

Giải thích:

TXĐ: $D=[-1;+\infty )$

$\begin{array}{l}{f}^{\text{'}}\left(1\right)=\underset{x\to 1}{\lim }\frac{f\left(x\right)-f\left(1\right)}{x-1}\\ =\underset{x\to 1}{\lim }\frac{\sqrt{x+1}-\sqrt{2}}{x-1}\\ =\underset{x\to 1}{\lim }\frac{x+1-2}{(x-1)(\sqrt{x+1}+\sqrt{2})}\\ =\underset{x\to 1}{\lim }\frac{1}{\sqrt{x+1}+\sqrt{2}}\\ =\frac{1}{2\sqrt{2}}=\frac{\sqrt{2}}{4}\end{array}$

Câu 6: Cho hàm số $f\left(x\right)$ là hàm số trên R định bởi $f\left(x\right)=x^2$ và $x_0\in R$. Chọn câu đúng

A. $f^{\text{'}}\left(x_0\right)=x_0$ 

B. $f^{\text{'}}\left(x_0\right)=x_0^2$

C. $f^{\text{'}}\left(x_0\right)=2x_0$

D. $f^{\text{'}}\left(x_0\right)$ không tồn tại.

Hiển thị đáp án  

Đáp án: C

Giải thích:

Giả sử $\text{Δ}x$ là số gia của đối số tại $x_0$.

Ta có 

$\begin{array}{l}\Delta y=f(x_0+\Delta x)-f\left(x_0\right)\\ ={\left(x_0+\text{Δ}x\right)}^2-x_0^2\\ =\text{Δ}x\left(2x_0+\text{Δ}x\right)\end{array}$

$\underset{\Delta x\to 0}{\lim }\frac{\Delta y}{\Delta x}=\underset{\Delta x\to 0}{\lim }(2x_0+\Delta x)=2x_0$

Vậy $f\text{'}\left(x_0\right)=2x_0$

Câu 7: Cho hàm số $\left\{\begin{array}{l}f\left(x\right)=3-\sqrt{4-x}khix\ne 0\\ 1khix=0\end{array}\right.$ . Khi đó $f\text{'}\left(0\right)$ là kết quả nào sau đây?

A. $\frac{1}{4}$

B. $\frac{1}{16}$

C. $\frac{1}{2}$

D. 2

Hiển thị đáp án  

Đáp án: A

Giải thích:

$\begin{array}{l}f\text{'}\left(0\right)=\underset{x\to 0}{\lim }\frac{f\left(x\right)-f\left(0\right)}{x-0}\\ =\underset{x\to 0}{\lim }\frac{3-\sqrt{4-x}-1}{x}\\ =\underset{x\to 0}{\lim }\frac{2-\sqrt{4-x}}{x}\end{array}$

$\begin{array}{l}=\underset{x\to 0}{\lim }\frac{4-4+x}{x(2+\sqrt{4-x})}\\ =\underset{x\to 0}{\lim }\frac{1}{2+\sqrt{4-x}}=\frac{1}{4}\end{array}$

Câu 8: Cho hàm số $f\left(x\right)=\left\{\begin{array}{l}\frac{3-\sqrt{4-x}}{4}khix\ne 0\\ \frac{1}{4}khix=0\end{array}\right..$Tính $f\text{'}\left(0\right)$.

A. $f^{\text{'}}\left(0\right)=\frac{1}{4}.$ 

B.  $f^{\text{'}}\left(0\right)=\frac{1}{16}.$

C. $f^{\text{'}}\left(0\right)=\frac{1}{32}.$ 

D.   Không tồn tại

Hiển thị đáp án  

Đáp án: B

Giải thích:

Xét

 $\begin{array}{l}\underset{x\to 0}{\lim }\frac{f\left(x\right)-f\left(0\right)}{x-0}\\ =\underset{x\to 0}{\lim }\frac{\frac{3-\sqrt{4-x}}{4}-\frac{1}{4}}{x}\\ =\underset{x\to 0}{\lim }\frac{2-\sqrt{4-x}}{4x}\end{array}$

$\begin{array}{l}=\underset{x\to 0}{\lim }\frac{(2-\sqrt{4-x})(2+\sqrt{4-x})}{4x(2+\sqrt{4-x})}\\ =\underset{x\to 0}{\lim }\frac{x}{4x(2+\sqrt{4-x})}\\ =\underset{x\to 0}{\lim }\frac{1}{4(2+\sqrt{4-x})}=\frac{1}{16}.\end{array}$

Câu 9: Cho hàm số $f\left(x\right)$ xác định trên $\left(0;+\infty \right)$ bởi $f\left(x\right)=\frac{1}{x}$. Đạo hàm của $f\left(x\right)$ tại $x_0=\sqrt{2}$ là

A. $\frac{1}{2}$

B. $-\frac{1}{2}$

C. $\frac{1}{\sqrt{2}}$

D. $-\frac{1}{\sqrt{2}}$

Hiển thị đáp án  

Đáp án: B

Giải thích:

Giả sử $\Delta x$ là số gia của đối số tại $x_0$.

Ta có 

$\begin{array}{l}\Delta y=f(x_0+\Delta x)-f\left(x_0\right)\\ =\frac{1}{x_0+\Delta x}-\frac{1}{x_0}\\ =-\frac{\text{Δ}x}{x_0\left(x_0+\text{Δ}x\right)}\end{array}$.

$\begin{array}{l}\underset{\text{Δ}x\to 0}{\lim }\frac{\text{Δ}y}{\text{Δ}x}\\ =\underset{\text{Δ}x\to 0}{\lim }\left(-\frac{1}{x_0\left(x_0+\text{Δ}x\right)}\right)\\ =-\frac{1}{x_0^2}\end{array}$.

Vậy $f\text{'}\left(x_0\right)=\frac{-1}{x_0^2}\Rightarrow f\text{'}\left(\sqrt{2}\right)=-\frac{1}{2}$.

Câu 10: Tính tỷ số $\frac{\text{Δ}y}{\text{Δ}x}$ của hàm số $y=2x^3$ theo x và $\text{Δ}x$.

A. $\frac{\text{Δ}y}{\text{Δ}x}=\frac{2x^3-2{\left(\text{Δ}x\right)}^3}{\text{Δ}x}.$

B. $\frac{\text{Δ}y}{\text{Δ}x}=2{\left(\text{Δ}x\right)}^2.$

C. $\frac{\text{Δ}y}{\text{Δ}x}=6x^2+6x\text{Δ}x+2{\left(\text{Δ}x\right)}^2.$

D. $\frac{\text{Δ}y}{\text{Δ}x}=3x^2+3x\text{Δ}x+{\left(\text{Δ}x\right)}^2.$

Hiển thị đáp án  

Đáp án: C

Giải thích:

Ta có

$\begin{array}{l}\Delta y=f(x+\Delta x)-f\left(x\right)\\ =2{\left(x+∆x^3\right)}^3-2x^3\\ =6x^2\Delta x+6x{\left(∆x^{}\right)}^2+2{\left(∆x\right)}^3\end{array}$

$\Rightarrow \frac{\Delta y}{\Delta x}=6x^2+6x\Delta x+2{\left(\Delta x\right)}^2.$

Xem thêm các bài tổng hợp lý thuyết Toán lớp 11 đầy đủ, chi tiết khác:

Lý thuyết Ôn tập chương 4

Lý thuyết Quy tắc tính đạo hàm 

Lý thuyết Đạo hàm của hàm số lượng giác

Lý thuyết Đạo hàm cấp hai 

Lý thuyết Ôn tập chương 5