Lý thuyết Ôn tập chương 1 (mới 2023 + Bài Tập) - Toán 11

Lý thuyết Toán 11 Ôn tập chương 1

A. Lý thuyết

1. Định nghĩa phép biến hình

- Quy tắc đặt tương ứng mỗi điểm M của mặt phẳng với một điểm xác định duy nhất M’ của mặt phẳng đó được gọi là phép biến hình trong mặt phẳng.

- Nếu kí hiệu phép biến hình là F thì ta viết F(M) = M’ hay M’ = F(M) và gọi M’ là ảnh của điểm M qua phép biến hình F.

- Nếu ℋ  là một hình nào đó trong mặt phẳng thì ta kí hiệu ℋ ' = F(ℋ) là tập các điểm M’ = F(M), với mọi điểm M thuộc ℋ. Khi đó, ta nói F là biến hình ℋ  thành hình ℋ ', hay hình ℋ ' là ảnh của hình ℋ  qua phép biến hình F.

- Phép biến hình biến mỗi điểm M thành chính nó được gọi là phép đồng nhất.

Ví dụ. Cho trước đường thẳng d, với mỗi điểm M trong mặt phẳng, gọi M’ là điểm sao cho M’ đối xứng với M qua d.

Quy tắc đặt tương ứng điểm M với điểm M’ nêu trên là một phép biến hình vì chỉ có duy nhất 1 điểm M’ thỏa mãn yêu cầu.

2. Định nghĩa phép tịnh tiến

- Định nghĩa: Trong mặt phẳng, cho vectơ $\overrightarrow{v}$. Phép biến hình biến mỗi điểm M thành điểm M’ sao cho $\overrightarrow{MM\text{'}}=\overrightarrow{v}$ được gọi là phép tịnh tiến theo vectơ $\overrightarrow{v}$.

- Phép tịnh tiến theo vectơ  thường được kí hiệu là được gọi là vectơ tịnh tiến.

Vậy: $T_{\overrightarrow{v}}\left(M\right)=M\text{'}\iff \overrightarrow{MM\text{'}}=\overrightarrow{v}$.

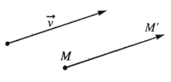
- Phép tịnh tiến theo vectơ – không chính là phép đồng nhất.

- Ví dụ 1. Cho hình vẽ sau:

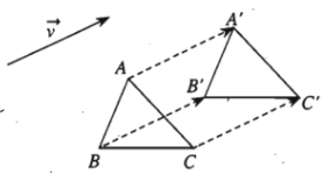
Ta có: $T_{\overrightarrow{v}}\left(A\right)=A\text{'};$$\hspace{0.17em}{T}_{\overrightarrow{v}}\left(B\right)=B\text{'};T_{\overrightarrow{v}}\left(C\right)=C\text{'}\hspace{0.17em}$.

3. Tính chất của phép tịnh tiến

- Tính chất 1.  Nếu $T_{\overrightarrow{v}}\left(M\right)=M\text{'};$$T_{\overrightarrow{v}}\left(N\right)=N\text{'}$ thì $\overrightarrow{M\text{'}N\text{'}}=\overrightarrow{MN}$ và từ đó suy ra M’N’ = MN.

Phép tịnh tiến bảo toàn khoảng cách giữa hai điểm bất kì.

- Tính chất 2. Phép tịnh tiến biến đường thẳng thành đường thẳng song song hoặc trùng với nó, biến đoạn thẳng thành đoạn thẳng bằng nó, biến tam giác thành tam giác bằng nó, biến đường tròn thành đường tròn có cùng bán kính.

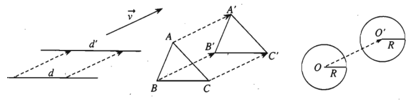
4. Biểu thức tọa độ của phép tịnh tiến

Trong mặt phẳng tọa độ Oxy cho vectơ $\overrightarrow{v}(a;b)$. Với mỗi điểm M(x ; y) ta có M’(x’ ; y’) là ảnh của điểm M qua tịnh tiến theo vectơ $\overrightarrow{v}$.

Khi đó:  

$$\begin{gathered} \overrightarrow{MM\text{'}}=\overrightarrow{v} \\ \iff \left\{\begin{array}{c}x\text{'}-x=a\\ y\text{'}-y=b\end{array}\right. \\ \Rightarrow \left\{\begin{array}{c}x\text{'}=x+a\\ y\text{'}=y+b\end{array}\right. \end{gathered}$$

đây chính là biểu thức tọa độ của phép tịnh tiến $T_{\overrightarrow{v}}$.

Ví dụ. Trong mặt phẳng tọa độ Oxy, cho điểm A(1 ; – 2). Phép tịnh tiến theo vectơ biến A thành điểm A’ có tọa độ là bao nhiêu?

Lời giải:

Gọi tọa độ điểm A’ = (x’; y’).

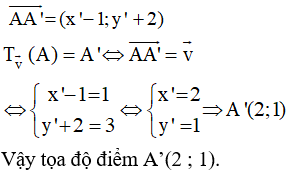
5. Định nghĩa của phép đối xứng trục

- Cho đường thẳng d. Phép biến hình biến mỗi điểm M thuộc d thành chính nó, biến mỗi điểm M không thuộc d thành điểm M’ sao cho d là đường trung trực của đoạn MM’ được gọi là phép đối xứng qua đường thẳng d hay phép đối xứng trục d.

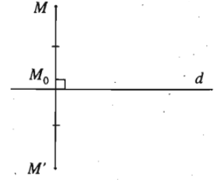
Đường thẳng d được gọi là trục của phép đối xứng hoặc đơn giản là trục đối xứng.

Phép đối xứng trục d thường được kí hiệu là Đ_d.

- Nếu hình ℋ ' là ảnh của hình ℋ  qua phép đối xứng trục d thì ta còn nói ℋ  đối xứng với ℋ ' qua d, hay ℋ  và ℋ ' đối xứng với nhau qua d.

- Nhận xét:

1) Cho đường thẳng d. Với mỗi điểm M, gọi M₀ là hình chiếu vuông góc của M

trên đường thẳng d. Khi đó: M’ = Đ_d(M) $\iff \overrightarrow{M_{0}M\text{'}}=-\overrightarrow{M_{0}M}$

2) M’ = Đ_d(M) $\iff$M = Đ_d(M’).

6. Biểu thức tọa độ của phép đối xứng trục

1) Chọn hệ trục tọa độ Oxy sao cho trục Ox trùng với đường thẳng d. Với mỗi điểm M = (x ; y), gọi M’ = Đ_d(M) = (x’ ; y’) thì $\left\{\begin{array}{c}x\text{'}=x\\ y\text{'}=-y\end{array}\right.$, đây là biểu thức tọa độ của phép đối xứng qua trục Ox. 

2) Chọn hệ trục tọa độ Oxy sao cho trục Oy trùng với đường thẳng d. Với mỗi điểm M = (x ; y), gọi M’ = Đ_d(M) = (x’; y’) thì $\left\{\begin{array}{c}x\text{'}=-x\\ y\text{'}=y\end{array}\right.$, đây là biểu thức tọa độ của phép đối xứng qua trục Oy.

Ví dụ. Cho điểm M(2 ; 4). Tìm ảnh của điểm M qua phép đối xứng qua trục Ox và trục Oy.

Lời giải:

Gọi Đ_Ox(M) = A(x ; y) và Đ_Oy(M) = B(a; b)

Áp dụng biểu thức tọa độ của phép đối xứng trục Ox ta có:

$$\begin{gathered} \left\{\begin{array}{c}x=2\\ y=-4\end{array}\right. \\ \Rightarrow A(2;-4) \end{gathered}$$

Áp dụng biểu thức tọa độ của phép đối xứng trục Oy ta có:

$\left\{\begin{array}{c}a=-2\\ b=4\end{array}\Rightarrow B(-2;4)\right.$

7. Tính chất của phép đối xứng trục

- Tính chất 1. Phép đối xứng trục bảo toàn khoảng cách giữa hai điểm bất kì.

- Tính chất 2. Phép đối xứng trục biến đường thẳng thành đường thẳng, biến đoạn thẳng thành đoạn thẳng bằng nó, biến tam giác thành tam giác bằng nó, biến đường tròn thành đường tròn có cùng bán kính.

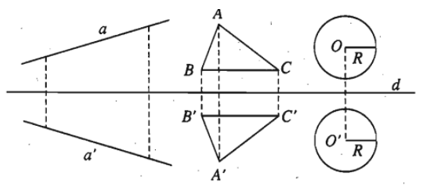
Ví dụ. Trong mặt phẳng tọa độ Oxy, qua phép đối xứng trục Ox, đường tròn (C)

(x – 2)² + (y – 3)² = 36 biến thành đường tròn (C’). Tìm phương trình đường tròn (C’) ?

Lời giải:

Đường tròn (C) có tâm I(2 ; 3) và bán kính là R = 6.

Qua phép đối xứng trục Ox, biến đường tròn (C) thành đường tròn (C’), biến tâm I thành tâm I’(x’; y’) và bán kính R’ = R = 6.

Áp dụng biểu thức phép đối xứng trục Ox ta được I’(2; – 3)

Do đó, phương trình đường tròn (C’) là:

(x – 2)² + (y + 3)² = 36.

8. Trục đối xứng của một hình

- Định nghĩa. Đường thẳng d được gọi là trục đối xứng của hình ℋ nếu phép đối xứng qua đường thẳng d biến ℋ thành chính nó.

Khi đó, ta nói ℋ là hình có trục đối xứng.

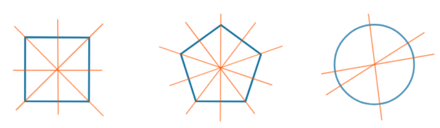
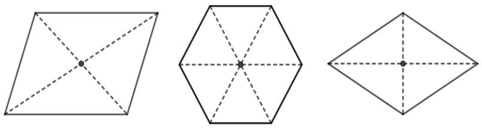
- Ví dụ 3. Các hình sau có trục đối xứng

9. Định nghĩa của phép đối xứng tâm

- Cho điểm I. Phép biến hình biến điểm I thành chính nó, biến mỗi điểm M khác điểm I thành điểm M’ sao cho I là trung điểm của đoạn thẳng MM’ được gọi là phép đối xứng tâm I.

Điểm I được gọi là tâm đối xứng.

Phép đối xứng tâm I thường được kí hiệu là Đ_I.

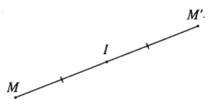
- Nếu hình ℋ ' là ảnh của hình ℋ  qua Đ_I thì ta còn nói ℋ  đối xứng với ℋ ' qua tâm I, hay ℋ  và ℋ ' đối xứng với nhau qua I.

Từ định nghĩa trên ta suy ra, M’ = Đ_I(M) $\iff \overrightarrow{IM\text{'}}=-\overrightarrow{IM}$.

- Ví dụ 1. Cho hình vẽ sau. Các điểm A và B là ảnh của điểm A’ và B’ qua phép đối xứng tâm I và ngược lại.

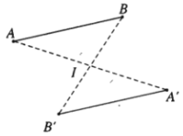
10. Biểu thức tọa độ của phép đối xứng qua gốc tọa độ

Trong hệ tọa độ Oxy, cho M(x ; y), M’= Đ_O(M) = (x’; y’). Khi đó:

 $\left\{\begin{array}{c}x\text{'}=-x\\ y\text{'}=-y\end{array}\right.$, đây là biểu thức tọa độ của phép đối xứng qua gốc tọa độ.

- Ví dụ. Trong mặt phẳng tọa độ Oxy cho điểm A(7 ; – 4). Tìm ảnh của điểm A qua phép đối xứng tâm O. 

Lời giải:

Gọi A’(x’; y’) là ảnh của điểm A qua  phép đối xứng tâm O. 

Áp dụng biểu thức tọa độ của phép đối xứng qua gốc tọa độ ta có:

$$\begin{gathered} \left\{\begin{array}{c}x\text{'}=-7\\ y\text{'}=-(-4)=4\end{array}\right. \\ \hspace{0.17em}\Rightarrow A\text{'}(-7;4) \end{gathered}$$

11. Tính chất của phép đối xứng tâm

- Tính chất 1. Nếu Đ_I(M) = M’ và Đ_I(N) = N’ thì $\overrightarrow{M\text{'}N\text{'}}=-\overrightarrow{MN}$, từ đó suy ra M’N’ = MN.

Phép đối xứng tâm bảo toàn khoảng cách giữa hai điểm bất kì.

- Tính chất 2. Phép đối xứng tâm biến đường thẳng thành đường thẳng song song hoặc trùng với nó, biến đoạn thẳng thành đoạn thẳng bằng nó, biến tam giác thành tam giác bằng nó, biến đường tròn thành đường tròn có cùng bán kính.

- Ví dụ. Trong mặt phẳng tọa độ Oxy, cho đường thẳng d: x + y – 2 = 0. Tìm ảnh của d qua phép đối xứng tâm I(1; 2).

Lời giải:

Giả sử phép đối xứng tâm I(1 ; 2) biến điểm  thành điểm M’(x’ ; y’).

Khi đó I là trung điểm của MM’. Áp dụng công thức tọa độ trung điểm ta có:

$$\begin{gathered} \left\{\begin{array}{l}{x}^{\text{'}}=2.1-x=2-x\\ y^{\text{'}}=2.2-y=4-y\end{array}\right. \\ \iff \left\{\begin{array}{l}x=2-x^{\text{'}}\\ y=4-y^{\text{'}}\end{array}\right. \end{gathered}$$

Vì điểm M thuộc d nên: x + y – 2 = 0    (2).

Thay (1) vào (2) ta được:

(2 – x’) + (4 – y’) – 2 = 0 hay – x’ – y’ + 4 = 0.

Do đó, phương trình đường thẳng d’ là – x – y + 4 = 0 hay x + y – 4 =0.

12. Tâm đối xứng của một hình

Định nghĩa. Điểm I được gọi là tâm đối xứng của hình ℋ nếu phép đối xứng tâm I biến hình ℋ  thành chính nó.

- Khi đó, ta nói ℋ  là hình có tâm đối xứng.

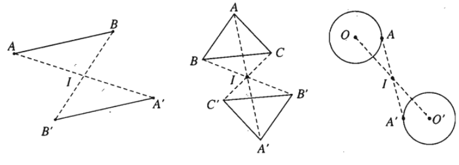
- Ví dụ 4. Các hình sau đây đều có tâm đối xứng:

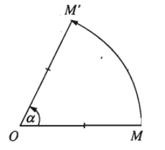
13. Định nghĩa của phép quay

- Định nghĩa: Cho điểm O và góc lượng giác α. Phép biến hình biến O thành chính nó, biến mỗi điểm M khác O thành điểm M’ sao cho OM’ = OM và góc lượng giác (OM; OM’) bằng α được gọi là phép quay tâm O góc α.

- Điểm O được gọi là tâm quay, α được gọi là góc quay của phép quay đó.

Phép quay tâm O góc α được kí hiệu là Q_{(O, α).}

- Nhận xét:

1) Chiều dương của phép quay là chiều dương của đường tròn lượng giác nghĩa là chiều ngược với chiều quay của kim đồng hồ.

2) Với k là số nguyên ta luôn có:

Phép quay $Q_{(O,k2\pi )}$ là phép đồng nhất.

Phép quay $Q_{(O,(2k\text{}+1\left)\pi \right)}$ là phép đối xứng tâm O.

14. Tính chất của phép quay

- Tính chất 1. Phép quay bảo toàn khoảng cách giữa hai điểm bất kì.

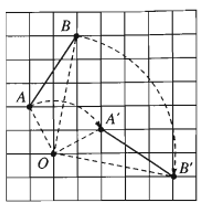
Phép quay tâm O, góc (OA, OA’) biến điểm A thành A’, B thành B’. Khi đó ta có A’B’ = AB.

- Tính chất 2. Phép quay biến đường thẳng thành đường thẳng, biến đoạn thẳng thành đoạn thẳng bằng nó, biến tam giác thành tam giác bằng nó, biến đường tròn thành đường tròn có cùng bán kính.

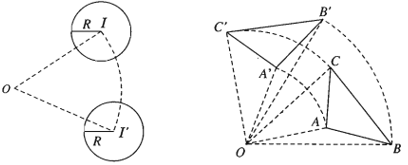
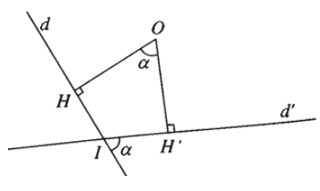
- Nhận xét: Phép quay góc α với , biến đường thẳng d thành đường thẳng d’ sao cho góc giữa d và d’ bằng α (nếu $0<\alpha \le \frac{\pi }{2}$), hoặc bằng $\mathrm{\pi }-\mathrm{\alpha }$ (nếu  $\frac{\pi }{2}\le \alpha <\pi )$

15. Khái niệm về phép dời hình

- Định nghĩa: Phép dời hình là phép biến hình bảo toàn khoảng cách giữa hai điểm bất kì.

Nếu phép dời hình F biến các điểm M, N lần lượt thành các điểm M’; N’ thì

MN = M’N’.

- Nhận xét:

1) Các phép đồng nhất, tịnh tiến, đối xứng trục, đối xứng tâm và phép quay đều là những phép dời hình.

2) Phép biến hình có được bằng cách thực hiện liên tiếp hai phép dời hình cũng là một phép dời hình.

- Ví dụ 1. Vì phép tịnh tiến và phép đối xứng tâm là phép dời hình nên thực hiện liên tiếp phép tịnh tiến theo vectơ  và phép đối xứng tâm O ta được một phép dời hình.

16. Tính chất của phép dời hình

Phép dời hình:

1) Biến ba điểm thẳng hàng thành ba điểm thẳng hàng và bảo toàn thứ tự giữa các điểm.

2) Biến đường thẳng thành đường thẳng, biến tia thành tia, biến đoạn thẳng thành đoạn thẳng bằng nó.

3) Biến tam giác thành tam giác bằng nó, biến góc thành góc bằng nó.

4) Biến đường tròn thành đường tròn có cùng bán kính.

- Chú ý:

a) Nếu một phép dời hình biến tam giác ABC thành tam giác A’B’C’ thì nó cũng biến trọng tâm, trực tâm, tâm đường tròn nội tiếp, ngoại tiếp của tam giác ABC tương ứng thành trọng tâm, trực tâm, tâm đường tròn nội tiếp, ngoại tiếp của tam giác A’B’C’.

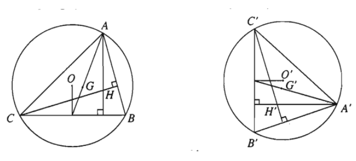
b) Phép dời hình biến đa giác n cạnh thành đa giác n cạnh, biến đỉnh thành đỉnh, biến cạnh thành cạnh.

- Ví dụ . Cho đường tròn (C) có phương trình (x + 4)² + (y – 3)² = 49. Thực hiện liên tiếp phép đối xứng trục qua đường thẳng d và phép quay tâm O góc quay 90⁰ ta được đường tròn (C’).

Bán kính đường tròn (C’) là: R’ = R = 7.

17. Khái niệm hai hình bằng nhau

- Định nghĩa. Hai hình được gọi là bằng nhau nếu có một phép dời hình biến hình này thành hình kia.

- Ví dụ.

a)  Qua phép tịnh tiến theo vectơ  biến tam giác ABC thành tam giác A’B’C’. Sau đó, ta thực hiện tiếp phép đối xứng trục qua đường thẳng d biến tam giác A’B’C’ thành tam giác A”B”C”. Khi đó: ∆ABC = ∆A”B”C”.

b) Hình ảnh dưới đây cho ta hai hình bằng nhau:

18. Định nghĩa của phép vị tự

- Cho điểm O và số k ≠ 0. Phép biến hình biến mỗi điểm M thành điểm M’ sao cho $\overrightarrow{OM\text{'}}=k.\overrightarrow{OM}$ được gọi là phép vị tự tâm O, tỉ số k.

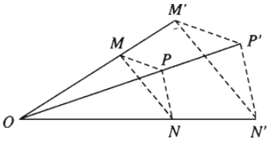
Phép vị tự tâm O tỉ số k thường được kí hiệu là V_{(O, k)}.

- Nhận xét:

1) Phép vị tự biến tâm vị tự thành chính nó.

2) Khi k = 1, phép vị tự là phép đồng nhất.

3) Khi k = -1, phép vị tự là phép đối xứng qua tâm vị tự.

4) M’ = V_{(O, k)}(M) $\iff M=V_{\left(O,\frac{1}{k}\right)}(M\text{'})$.

19. Tính chất của phép vị tự

- Tính chất 1. Nếu phép vị tự tỉ số k biến hai điểm M, N tùy ý theo thứ tự thành M’, N’ thì $\overrightarrow{M\text{'}N\text{'}}=k.\overrightarrow{MN}$ và M’N’ = |k|.MN.

- Tính chất 2.

Phép vị tự tỉ số k:

a) Biến ba điểm thẳng hàng thành ba điểm thẳng hàng và bảo toàn thứ tự giữa các điểm ấy.

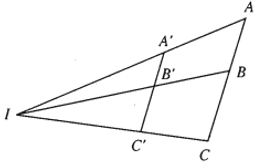
b) Biến đường thẳng thành đường thẳng song song hoặc trùng với nó, biến tia thành tia, biến đoạn thẳng thành đoạn thẳng.

c) Biến tam giác thành tam giác đồng dạng với nó, biến góc thành góc bằng nó.

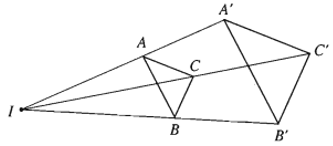
d) Biến đường tròn bán kính R thành đường tròn có bán kính |k|.R.

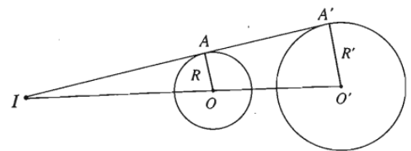
20. Tâm vị tự của hai đường tròn.

- Định lí: Với hai đường tròn bất kì luôn có một phép vị tự biến đường tròn này thành đường tròn kia.

Tâm của phép vị tự được gọi là tâm vị tự của hai đường tròn.

- Cách tìm tâm vị tự của hai đường tròn.

Cho hai đường tròn (I ; R) và (I’; R’) có ba trường hợp xảy ra:

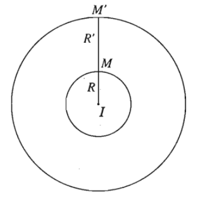
+ Trường hợp I trùng với I’

Khi đó, phép vị tự tâm I tỉ số $\frac{R\text{'}}{R}$ và phép vị tự tâm I tỉ số $-\frac{R\text{'}}{R}$ biến đường tròn

(I ; R) thành đường tròn (I ; R’).

+ Trường hợp I khác I’ và R ≠ R’

Lấy điểm M bất kì thuộc đường tròn (I ; R), đường thẳng qua I’ song song với IM cắt đường tròn (I’ ; R’) tại M’ và M”.

Giả sử M, M’ nằm cùng phía đối với đường thẳng II’ còn M, M” nằm khác phía đối với đường thẳng II’.

Giả sử đường thẳng MM’ cắt đường thẳng II’ tại điểm O nằm ngoài đoạn thẳng II’, còn đường thẳng MM” cắt đường thẳng II’ tại điểm O₁ nằm trong đoạn thẳng II’.

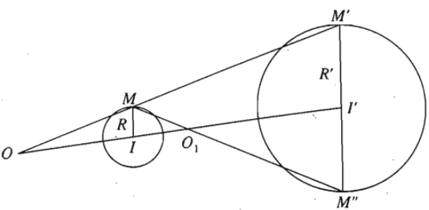
Khi đó, phép vị tự tâm O tỉ số $k=\frac{R\text{'}}{R}$ và phép vị tự tâm O₁ tỉ số $k_1=-\frac{R\text{'}}{R}$ sẽ biến đường tròn (I ; R) thành đường tròn (I’; R’).

Ta gọi O là tâm vị tự ngoài còn O₁ là tâm vị tự trong của hai đường tròn nói trên.

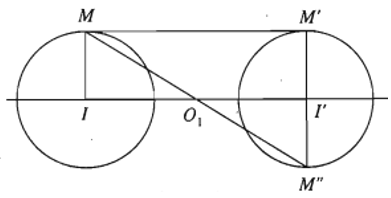
+ Trường hợp I khác I’ và R = R’.

Khi đó, MM’ // II’ nên chỉ có phép vi tự tâm O₁ tỉ số $k=\frac{-R}{R}=-1$ biến đường tròn (I; R) thành đường tròn (I’ ; R’). Đây chính là phép đối xứng tâm O₁.

Ví dụ 1. Cho hai đường tròn (C): (x – 2)² + (y – 1)² = 4 và (C’): (x – 8)² + (y – 4)² = 16. Xác định tâm vị tự của hai đường tròn?

Lời giải:

Đường tròn (C) có tâm I(2 ; 1),bán kính R = 1;

Đường tròn (C’) có tâm I’(8 ; 4), bán kính R’ = 4.

Do I  ≠  I’ và R ≠ R’ nên có hai phép vị tự V_{(J, 2)} và V_{(J, -2)} biến (C) thành (C’).

Gọi J(x ; y)

Với k = 2 khi đó:

$$\begin{gathered} \overrightarrow{JI\text{'}}=2\overrightarrow{JI} \\ \iff \left\{\begin{array}{l}8-x=2\left(2-x\right)\\ 4-y=2\left(1-y\right)\end{array}\right. \\ \iff \left\{\begin{array}{l}x=-4\\ y=-2\end{array}\right. \end{gathered}$$

Suy ra: J(– 4; – 2)

Tương tự với k = – 2, tính có J’(4; 2).

Vậy có 2 phép vị tự thỏa mãn đầu bài.

21. Định nghĩa phép đồng dạng

- Định nghĩa: Phép biến hình F được gọi là phép đồng dạng tỉ số k (k > 0), nếu với hai điểm M, N bất kì và ảnh M’, N’ tương ứng của chúng ta luôn có M’N’ = kMN.

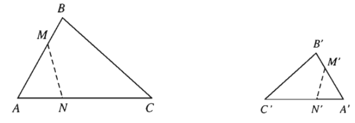
- Nhận xét

(1) Phép dời hình là phép đồng dạng tỉ số 1.

(2) Phép vị tự tỉ số k là phép đồng dạng tỉ số |k|.

22. Tính chất phép đồng dạng

Phép đồng dạng tỉ số k:

a) Biến ba điểm thẳng hàng thành ba điểm thẳng hàng và bảo toàn thứ tự giữa các điểm ấy.

b) Biến đường thẳng thành đường thẳng, biến tia thành tia, biến đoạn thẳng thành đoạn thẳng.

c) Biến tam giác thành tam giác đồng dạng với nó, biến góc thành góc bằng nó.

d) Biến đường tròn bán kính R thành đường tròn có bán kính kR.

- Chú ý.

a) Nếu một phép đồng dạng biến tam giác ABC thành tam giác A’B’C’ thì nó cũng biến trọng tâm, trực tâm, tâm đường tròn nội tiếp, ngoại tiếp của tam giác ABC tương ứng thành trọng tâm, trực tâm, tâm đường tròn nội tiếp, ngoại tiếp của tam giác A’B’C’.

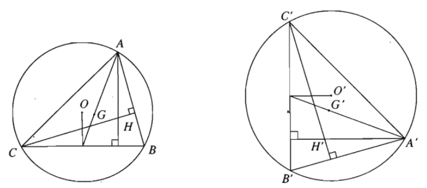
b) Phép đồng dạng biến đa giác n cạnh thành đa giác n cạnh, biến đỉnh thảng đỉnh, biến cạnh thành cạnh.

Ví dụ. Trong mặt phẳng với hệ trục tọa độ Oxy, cho 2 đường tròn (C) và (C’) có phương trình x² + y² – 4y – 5 = 0 và x² + y² – 2x + 2y – 14 = 0. Gọi (C’) là ảnh của (C) qua phép đồng dạng tỉ số k, khi đó giá trị k là ?

Lời giải:

Đường tròn (C) có tâm I(0 ; 2) bán kính R = 3.

Đường tròn (C’) có tâm I’(1 ; – 1) bán kính R’ = 4.

Ta có (C’) là ảnh của (C) qua phép đồng dạng tỉ số k nên : 4 = 3k

Suy ra : $k=\frac{4}{3}$ .

Vậy $k=\frac{4}{3}$.

23. Hình đồng dạng

- Định nghĩa. Hai hình được gọi là đồng dạng với nhau nếu có một phép đồng dạng biến hình này thành hình kia.

- Ví dụ. Các hình sau đôi một đồng dạng với nhau.

B. Bài tập tự luyện

Bài 1. Cho phép tịnh tiến $T_{\overrightarrow{u}}$ biến điểm M thành M₁ và phép tịnh tiến $T_{\overrightarrow{v}}$ biến M₁ thành M₂. Hỏi tịnh tiến theo vectơ $(\overrightarrow{u}+\text{\hspace{0.17em}}\overrightarrow{v})$ biến điểm M thành điểm nào?

Lời giải:

Theo giả thiết ta có:

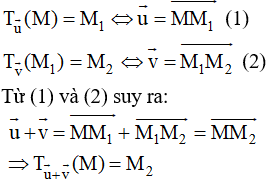
Vậy tịnh tiến theo vectơ$(\overrightarrow{u}+\text{\hspace{0.17em}}\overrightarrow{v})$ biến điểm M thành điểm M₂.

Bài 2. Trong mặt phẳng tọa độ Oxy, cho 2 điểm A(2; 1); B(– 1; – 4). Gọi C và D lần lượt là ảnh của A và B qua phép tịnh tiến theo vectơ $\overrightarrow{v}(1;5)$. Tính độ dài đoạn thẳng CD?

Lời giải:

Ta có:

 $$\begin{gathered} AB=\sqrt{{(-1-2)}^2+\text{\hspace{0.17em}}{(-4-1)}^2} \\ =\sqrt{34} \end{gathered}$$

Vì $T_{\overrightarrow{v}}\left(A\right)=C;$$\hspace{0.17em}{T}_{\overrightarrow{v}}\left(B\right)=D$ nên theo tính chất của phép tịnh tiến ta có:

$CD=AB=\sqrt{34}$

Vậy $CD=\sqrt{34}$.

Bài 3. Trong mặt phẳng tọa độ Oxy, cho $\overrightarrow{v}(1;-3)$ và đường thẳng d có phương trình 2x – 3y + 5 =  0. Viết phương trình đường thẳng d’ là ảnh của d qua phép tịnh tiến $T_{\overrightarrow{v}}$.

Lời giải:

Cách 1. Sử dụng biểu thức tọa độ của phép tịnh tiến.

Lấy điểm M(x ; y) tùy ý thuộc d, ta có: 2x – 3y + 5 = 0  (1)

Gọi :

$$\begin{gathered} M\text{'}\left(x\text{'};y\text{'}\right)=T_{\overrightarrow{v}}\left(M\right) \\ \Rightarrow \left\{\begin{array}{l}x\text{'}=x+1\\ y\text{'}=y-3\end{array}\right. \\ \iff \left\{\begin{array}{l}x=x\text{'}-1\\ y=y\text{'}+3\end{array}\right. \end{gathered}$$

Thay vào (1) ta được phương trình:

2(x’ – 1) – 3(y’ + 3) + 5 = 0 hay 2x’ – 3y’ – 6 = 0.

Vậy ảnh của d là đường thẳng d’: 2x – 3y – 6 = 0.

Cách 2. Sử dụng tính chất của phép tịnh tiến

Do $T_{\overrightarrow{v}}\left(d\right)=d\text{'}$ nên d’ song song hoặc trùng với d.

Suy ra, phương trình đường thẳng d’ có dạng: 2x – 3y + c = 0      (2).

Lấy điểm M(– 1; 1) thuộc d.

Khi đó $T_{\overrightarrow{v}}\left(M\right)=M\text{'}(x\text{'};y\text{'})$.

$$\begin{gathered} \left\{\begin{array}{l}x\text{'}=-1+1=0\\ y\text{'}=1-3=-2\end{array}\right. \\ \Rightarrow M\text{'}(0;-2) \end{gathered}$$

Do M’ thuộc d’ nên thay tọa độ M’ vào d’ ta được:

2.0 – 3.(– 2) + c = 0 nên c = – 6.

Vậy ảnh của d là đường thẳng d’: 2x – 3y – 6 = 0.

Bài 4. Trong mặt phẳng tọa độ Oxy, cho đường tròn (C) có phương trình

 x² + y² + 2x – 4y – 4 = 0. Tìm ảnh của (C) qua phép tịnh tiến theo vectơ $\overrightarrow{v}(1;1)$.

Lời giải:

Sử dụng tính chất của phép tịnh tiến:

Đường tròn (C) có tâm I(–1 ; 2) và bán kính $R=\sqrt{{(-1)}^2+\text{\hspace{0.17em}}{2}^2-(-4)}=3$.

Gọi ảnh của (C) qua phép tịnh tiến theo vectơ  là (C’) có tâm I’(x’; y’) và  bán kính R’ = R = 3.

Ta tìm tâm I’(x’; y’).

Ta có:

 $$\begin{gathered} \left\{\begin{array}{c}x\text{'}=-1+1=0\\ y\text{'}=2+1=3\end{array}\right. \\ \Rightarrow I\text{'}(0;3) \end{gathered}$$

 Do đó, phương trình của đường tròn (C’) là x² + (y – 3)² = 9.

Bài 5. Mỗi hình sau có bao nhiêu trục đối xứng?

a) Hình gồm hai đường tròn có tâm và bán kính khác nhau.

b) Hình gồm hai đường thẳng d và d’ vuông góc với nhau.

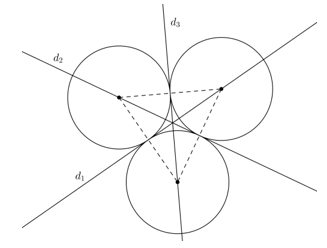
c) Hình gồm 3 đường tròn có bán kính bằng nhau và đôi một tiếp xúc ngoài với nhau.

Lời giải:

Một đường tròn có vô số trục đối xứng đi qua tâm của đường tròn đó.

Do đó, trục đối xứng thỏa yêu cầu của bài toán là đường thẳng nối hai tâm của đường tròn đã cho.

Vậy hình gồm hai đường tròn có tâm và bán kính khác nhau có 1 trục đối xứng.

b) Có bốn trục đối xứng gồm đường thẳng d; d’ và hai đường phân giác của hai góc tạo bởi d, d’.

c) Có 3 trục đối xứng là 3 đường trung trực của các đoạn nối tâm.

Bài 6. Trong mặt phẳng Oxy, cho điểm M(2 ; 3). Tìm ảnh của M qua phép đối xứng qua đường thẳng d: x – y = 0?

Lời giải:

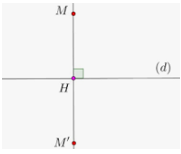
Gọi H là hình chiếu vuông góc của M trên d.

Ta có đường thẳng MH vuông góc với d nên đường thẳng MH có vectơ chỉ phương là:

$$\begin{gathered} \overrightarrow{u_{MH}}=\overrightarrow{n_d}=(1;-1) \\ \Rightarrow \overrightarrow{n_{MH}}=(1;1) \end{gathered}$$

Phương trình đường thẳng MH: 1.(x – 2) + 1.(y – 3) = 0 hay x + y – 5 = 0

Hai đường thẳng MH và d cắt nhau tại H nên tọa độ H là nghiệm hệ:

$\begin{array}{l}\left\{\begin{array}{c}x-y=0\\ x+y-5=0\end{array}\right.\\ \iff x=y=\frac{5}{2}\\ \Rightarrow H\left(\frac{5}{2};\frac{5}{2}\right)\end{array}$

Vì Đ_d(M) = M’ nên H là trung điểm của MM’.

$$\begin{gathered} \Rightarrow \left\{\begin{array}{c}{x}_{M\text{'}}=2x_H-x_M=3\\ y_{M\text{'}}=2y_H-y_M=2\end{array}\right. \\ \Rightarrow M\text{'}\left(3;2\right) \end{gathered}$$

Vậy M’(3; 2).

Bài 7. Trong mặt phẳng với hệ trục tọa độ Oxy, cho phép đối xứng trục Ox biến đường thẳng d: x + y – 2 = 0 thành đường thẳng d’. Viết phương trình d’.

Lời giải:

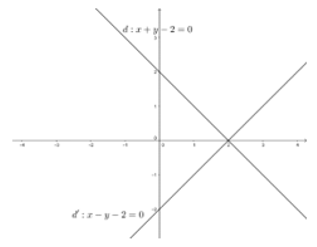
Lấy điểm M(x ; y) thuộc d suy ra:

x + y – 2 = 0  (1)

Gọi M’(x’; y’) là ảnh của M qua phép đối xứng trục Ox.

Khi đó ta có: $\left\{\begin{array}{c}x\text{'}=x\\ y\text{'}=-y\end{array}\right.$$\hspace{0.17em}\Rightarrow \left\{\begin{array}{c}x=x\text{'}\\ y=-y\text{'}\end{array}\right.$.  (2)

Thay (2) vào (1) ta được :

x’ – y’ – 2 = 0

Suy ra, phương trình đường thẳng d’ : x – y – 2 = 0.

Bài 8. Trong mặt phẳng tọa độ Oxy, cho đường thẳng đường tròn (C):

x² + y² – 2x – 4y – 4 =  0. Tìm ảnh của (C) qua phép đối xứng trục Oy.

Lời giải:

Đường tròn (C) có tâm I(1; 2) và bán kính $R=\sqrt{1^2+\text{\hspace{0.17em}\hspace{0.17em}}{2}^2-(-4)}=3$.

Gọi I’ và R’ là tâm và bán kính của (C’) là ảnh của đường tròn (C) qua phép đối xứng trục Oy.

Ta có: R’ = R = 3

Ta tìm tọa độ tâm I’.

Áp dụng biểu thức tọa độ của phép đối xứng trục Oy ta được I’(– 1; 2)

Phương trình đường tròn (C’): (x + 1)² + (y – 2)² = 9.

Bài 9. Mỗi hình sau có bao nhiêu trục đối xứng?

a) Hình gồm hai đường tròn có tâm và bán kính khác nhau.

b) Hình gồm hai đường thẳng d và d’ vuông góc với nhau.

c) Hình gồm 3 đường tròn có bán kính bằng nhau và đôi một tiếp xúc ngoài với nhau.

Lời giải:

Một đường tròn có vô số trục đối xứng đi qua tâm của đường tròn đó.

Do đó, trục đối xứng thỏa yêu cầu của bài toán là đường thẳng nối hai tâm của đường tròn đã cho.

Vậy hình gồm hai đường tròn có tâm và bán kính khác nhau có 1 trục đối xứng.

b) Có bốn trục đối xứng gồm đường thẳng d; d’ và hai đường phân giác của hai góc tạo bởi d, d’.

c) Có 3 trục đối xứng là 3 đường trung trực của các đoạn nối tâm.

Bài 10. Trong mặt phẳng Oxy, cho điểm M(2 ; 3). Tìm ảnh của M qua phép đối xứng qua đường thẳng d: x – y = 0?

Lời giải:

Gọi H là hình chiếu vuông góc của M trên d.

Ta có đường thẳng MH vuông góc với d nên đường thẳng MH có vectơ chỉ phương là:

$$\begin{gathered} \overrightarrow{u_{MH}}=\overrightarrow{n_d}=(1;-1) \\ \Rightarrow \overrightarrow{n_{MH}}=(1;1) \end{gathered}$$

Phương trình đường thẳng MH: 1.(x – 2) + 1.(y – 3) = 0 hay x + y – 5 = 0

Hai đường thẳng MH và d cắt nhau tại H nên tọa độ H là nghiệm hệ:

$\begin{array}{l}\left\{\begin{array}{c}x-y=0\\ x+y-5=0\end{array}\right.\\ \iff x=y=\frac{5}{2}\\ \Rightarrow H\left(\frac{5}{2};\frac{5}{2}\right)\end{array}$

Vì Đ_d(M) = M’ nên H là trung điểm của MM’.

$$\begin{gathered} \Rightarrow \left\{\begin{array}{c}{x}_{M\text{'}}=2x_H-x_M=3\\ y_{M\text{'}}=2y_H-y_M=2\end{array}\right. \\ \Rightarrow M\text{'}\left(3;2\right) \end{gathered}$$

Vậy M’(3; 2).

Bài 11. Trong mặt phẳng với hệ trục tọa độ Oxy, cho phép đối xứng trục Ox biến đường thẳng d: x + y – 2 = 0 thành đường thẳng d’. Viết phương trình d’.

Lời giải:

Lấy điểm M(x ; y) thuộc d suy ra:

x + y – 2 = 0  (1)

Gọi M’(x’; y’) là ảnh của M qua phép đối xứng trục Ox.

Khi đó ta có: $\left\{\begin{array}{c}x\text{'}=x\\ y\text{'}=-y\end{array}\right.$$\hspace{0.17em}\Rightarrow \left\{\begin{array}{c}x=x\text{'}\\ y=-y\text{'}\end{array}\right.$.  (2)

Thay (2) vào (1) ta được :

x’ – y’ – 2 = 0

Suy ra, phương trình đường thẳng d’ : x – y – 2 = 0.

Bài 12. Trong mặt phẳng tọa độ Oxy, cho đường thẳng đường tròn (C):

x² + y² – 2x – 4y – 4 =  0. Tìm ảnh của (C) qua phép đối xứng trục Oy.

Lời giải:

Đường tròn (C) có tâm I(1; 2) và bán kính $R=\sqrt{1^2+\text{\hspace{0.17em}\hspace{0.17em}}{2}^2-(-4)}=3$.

Gọi I’ và R’ là tâm và bán kính của (C’) là ảnh của đường tròn (C) qua phép đối xứng trục Oy.

Ta có: R’ = R = 3

Ta tìm tọa độ tâm I’.

Áp dụng biểu thức tọa độ của phép đối xứng trục Oy ta được I’(– 1; 2)

Phương trình đường tròn (C’): (x + 1)² + (y – 2)² = 9.

Bài 13. Cho hình vuông tâm O. Hỏi có bao nhiêu phép quay tâm O góc quay α với  biến hình vuông trên thành chính nó?

Lời giải:

Có 4 phép quay tâm O góc α với $0<\alpha \le 2\pi$ biến hình vuông trên thành chính nó. Đó là các phép quay với góc quay bằng: $\frac{\pi }{2};\pi ;\frac{3\pi }{2};2\pi .$

Khi đó, các phép quay biến đỉnh này thành đỉnh kia của hình vuông.

Bài 14. Trong mặt phẳng Oxy cho điểm A(9; 0). Tìm tọa độ ảnh A’ của điểm A qua phép quay $Q_{(O,\frac{\pi }{2})}$.

Lời giải:

Cách 1: Biểu diễn phép quay trên mặt phẳng tọa độ, suy ra A’(0; 9).

Cách 2. Áp dụng biểu thức tọa độ của phép quay (mở rộng)

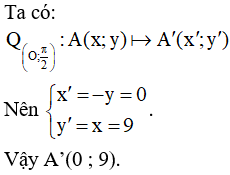
Bài 15. Tìm ảnh của đường thẳng d: 5x – 3y + 15 = 0 qua phép quay tâm O và  góc quay 90⁰.

Lời giải:

Gọi d’ là ảnh cuả đường thẳng d qua phép quay trên.

Vì góc quay 90⁰ nên $d\perp d\text{'}$.

Suy ra, phương trình đường thẳng d’ có dạng:  3x + 5y + c = 0

Lấy điểm M(– 3 ; 0) thuộc d.

Ta có $Q_{\left(0;{90}^0\right)}\left(M\right)=M\text{'}\left(0;-3\right)$

Vì điểm M’ thuộc d’ nên thay tọa độ điểm M’ vào d’ ta được:

3.0 + 5.(– 3) + c = 0 nên c = 15.

Vậy phương trình đường thẳng d’ là 3x + 5y + 15 = 0.

Bài 16. Cho đường thẳng d: 3x + y + 3 = 0. Viết phương trình của đường thẳng d’ là ảnh của d qua phép dời hình có được bằng cách thực hiện liên tiếp phép đối xứng tâm I(1 ; 2) và phép tịnh tiến theo vectơ $\overrightarrow{v}(-2;1)$.

Lời giải:

Gọi F là phép dời hình có được bằng cách thực hiện liên tiếp phép đối xứng tâm I và phép tịnh tiến theo $\overrightarrow{v}(-2;1)$.

Gọi $d_1={Ð}_I\left(d\right),d\text{'}=T_{\overrightarrow{v}}\left(d_1\right)$$\Rightarrow d\text{'}=F\left(d\right)$.

Do d’ song song hoặc trùng với d do đó phương trình của d’ có dạng 3x + y + c = 0 - Lấy M(0 ; – 3) ta có Đ_I(M) = M’. Khi đó, I là trung điểm MM’.

Áp dụng biểu thức tọa độ trung điểm ta có tọa độ của M’ là:

$$\begin{gathered} \left\{\begin{array}{c}x\text{'}=2.1-0=2\\ y\text{'}=2.2-(-3)=7\end{array}\right. \\ \hspace{0.17em}\Rightarrow M\text{'}(2;7) \end{gathered}$$

- Tịnh tiến theo $\overrightarrow{v}(-2;1)$ biến M’ thành M”. Áp dụng biểu thức tọa độ của phép tịnh tiến ta được: M”(0 ; 8)

Mà M” thuộc d’ nên thay tọa độ M” vào d’ ta được:

3.0 + 8 + c = 0 nên c = – 8.

Vậy phương trình đường thẳng d’ là 3x + y – 8 = 0.

Bài 17. Trong mặt phẳng Oxy, cho điểm M(2 ; 1). Hỏi phép dời hình có được bằng cách thực hiện liên tiếp phép đối xứng tâm O(0; 0) và phép tịnh tiến theo vectơ $\overrightarrow{v}(2;3)$ biến điểm M thành điểm nào?

Lời giải:

+ Gọi Đ_O(M) = M’.

Suy ra, O là trung điểm của MM’.

$$\begin{gathered} \iff \left\{\begin{array}{l}{x}_M+x_{M^{\text{'}}}=2x_O\\ y_M+y_{M^{\text{'}}}=2y_O\end{array}\right. \\ \iff M^{\text{'}}(-2;-1) \end{gathered}$$

+ Thực hiện phép tịnh tiến theo vectơ  biến M’ thành M”

$$\begin{gathered} \iff \overrightarrow{M^{\text{'}}{M^{\text{'}}}^{\text{'}}}=\overrightarrow{v} \\ \iff \left\{\begin{array}{l}{x}_{{M^{\text{'}}}^{\text{'}}}-x_{M^{\text{'}}}=2\\ y_{{M^{\text{'}}}^{\text{'}}}-y_{M^{\text{'}}}=3\end{array}\right. \\ \iff {M^{\text{'}}}^{\text{'}}(0;2) \end{gathered}$$

Vậy khi ta thực hiện liên tiếp phép đối xứng và phép tịnh tiến trên biến M thành M”(0 ; 2).

Bài 18. Trong mặt phẳng Oxy, cho đường tròn (C) có phương trình x² + y² – 2x + 4y + 1 = 0. Hỏi phép dời hình có được bằng cách thực hiện liên tiếp phép đối xứng qua trục Oy và phép tịnh tiến theo vectơ $\overrightarrow{v}(2;3)$ biến (C) thành đường tròn nào?

Lời giải :                      

Đường tròn (C) có tâm I(1 ; – 2) và bán kính $R=\sqrt{1^2+\text{\hspace{0.17em}}{(-2)}^2-1}=2$.

+ Thực hiện phép đối xứng qua trục Oy biến tâm I thành tâm I’(– 1 ; – 2) ; R’ = R = 2.

+ Thực hiện phép tịnh tiến theo vectơ $\overrightarrow{v}(2;3)$ biến I’ thành I”

Áp dụng biểu thức tọa độ của phép tịnh tiến ta được I’’(1 ; 1) và R’’ = R’ = 2.

Vậy đường tròn cần tìm có tâm I’’(1 ; 1) và bán kính R’’ = 2.

Phương trình (C’’) : (x – 1)² + (y – 1)² = 4.

Bài 19. Cho tam giác ABC với trọng tâm G. Gọi A’, B’, C’ lần lượt là trung điểm của các cạnh BC, AC, AB của tam giác ABC. Khi đó phép vị tự nào biến tam giác A’B’C’ thành tam giác ABC?

Lời giải :

Vì G là trọng tâm tam giác ABC nên:

  $$\begin{gathered} \overrightarrow{GA}=-2\overrightarrow{G{A}^{\text{'}}},\overrightarrow{GB}=-2\overrightarrow{G{B}^{\text{'}}}, \\ \overrightarrow{GC}=-2\overrightarrow{G{C}^{\text{'}}}. \end{gathered}$$

Bởi vậy phép vị tự V_{(G; -2)} biến tam giác A’B’C’ thành tam giác ABC.

Bài 20. Trong măt phẳng tọa độ Oxy, cho điểm M(– 2 ; 4). Phép vị tự tâm O(0 ; 0) tỉ số k = – 2 biến điểm M thành điểm nào?

Lời giải:

Nếu $V_{(O;k)}:M(x;y)$$\mapsto M^{\text{'}}(x^{\text{'}};y^{\text{'}})$ thì

$$\begin{gathered} \overrightarrow{OM\text{'}}=-2\overrightarrow{OM} \\ \Rightarrow \left\{\begin{array}{c}x\text{'}=-2x=4\\ y\text{'}=-2y=-8\end{array}\right. \\ \Rightarrow M\text{'}(4;-8) \end{gathered}$$

Vậy điểm cần tìm là M’(4 ; – 8).

Bài 21. Trong mặt phẳng Oxy cho đường thẳng d có phương trình 2x + y – 3 =  0. Phép vị tự tâm O(0; 0) tỉ số k = 2 biến d thành đường thẳng có phương trình là gì?

Lời giải:

Thực hiện phép vị tự tâm O(0; 0) tỉ số k = 2 biến d thành đường thẳng d’. Suy ra d’ song song hoặc trùng với d.

Do đó, d’ có dạng  2x + y + c = 0  (1)

Lấy điểm M(1 ; 1) thuộc d.

Gọi V_{(O ; 2)}(M) = M’(x’ ; y’)

$$\begin{gathered} \overrightarrow{OM\text{'}}=2\overrightarrow{OM} \\ \Rightarrow \left\{\begin{array}{c}x\text{'}=2x=2\\ y\text{'}=2y=2\end{array}\right. \\ \Rightarrow M\text{'}(2;2) \end{gathered}$$

Điểm M’ thuộc d’ nên thay tọa độ M’ vào d’ ta được :

2.2 + 2 + c = 0 nên c = – 6.

Vậy phương trình đường thẳng d’ cần tìm là 2x + y – 6 = 0.

Bài 22. Trong mặt phẳng tọa độ Oxy, cho đường tròn (C) : (x  – 1)² + (y – 1)² = 4. Tìm ảnh của đường tròn (C) qua phép vị tự tâm I(– 1 ; 2) tỉ số k = 3.

Lời giải:

Đường tròn (C)  có tâm A(1; 1), bán kính R = 2.

Gọi $A\text{'}\left(x\text{'};y\text{'}\right)=V_{\left(I;3\right)}\left(A\right)$

$$\begin{gathered} \Rightarrow \overrightarrow{IA\text{'}}=3\overrightarrow{IA} \\ \iff \left\{\begin{array}{l}x\text{'}+1=3\left(1+1\right)\\ y\text{'}-2=3\left(1-2\right)\end{array}\right. \\ \iff \left\{\begin{array}{l}x\text{'}=5\\ y\text{'}=-1\end{array}\right. \end{gathered}$$

Do đó, A’(5 ; – 1)

Gọi (C’) là ảnh của (C) qua phép vị tự V thì (C’) có tâm A’, bán kính R’ = 3R = 6.

Vậy phương trình (C’): (x – 5)² + (y + 1)² = 36.

Bài 23. Trong mặt phẳng với hệ trục tọa độ Oxy cho A(– 2 ; – 3); B(4 ; 1). Phép đồng dạng tỉ số $k=\frac{1}{2}$ biến điểm A thành A’, biến điểm B thành B’. Khi đó độ dài A’B’ là bao nhiêu?

Lời giải:

Vì phép đồng dạng tỉ số $k=\frac{1}{2}$ biến điểm A thành A’, biến điểm B thành B’ nên 

$$\begin{gathered} A^{\text{'}}{B}^{\text{'}}=\frac{1}{2}AB \\ =\frac{1}{2}\sqrt{{\left(4+2\right)}^2+{\left(1+3\right)}^2} \\ =\frac{\sqrt{52}}{2}=\frac{2\sqrt{13}}{2}=\sqrt{13} \end{gathered}$$

Bài 24. Trong mặt phẳng Oxy, cho điểm M(2 ; 4). Phép đồng dạng có được bằng cách thực hiện liên tiếp phép vị tự tâm O(0 ; 0) tỉ số $k=\frac{1}{2}$ và phép đối xứng qua trục Oy sẽ biến M thành điểm nào?

Lời giải:

Gọi $M^{\text{'}}=V_{\left(O,\frac{1}{2}\right)}\left(M\right);$ $M^{\text{'}\text{'}}={Đ}_{Oy}\left(V_{\left(O;\frac{1}{2}\right)}\left(M\right)\right).$

Tọa độ điểm M’ là:

$$\begin{gathered} \overrightarrow{OM\text{'}}=\frac{1}{2}\overrightarrow{OM} \\ \Rightarrow \left\{\begin{array}{c}{x}^{\text{'}}=2.\frac{1}{2}=1\\ y^{\text{'}}=4.\frac{1}{2}=2\end{array}\right. \\ \Rightarrow M\text{'}(1;2) \end{gathered}$$

Áp dụng biểu thức tọa độ của phép đối xứng qua trục Oy ta có:

Tọa độ điểm M” là: $\left\{\begin{array}{c}x"=-x\text{'}\\ y"=y\text{'}\end{array}\right.\iff \left\{\begin{array}{c}x"=-1\\ y"=2\end{array}\right..$

Vậy điểm M” cần tìm là M” (– 1 ; 2).

Trắc nghiệm Toán 11 Bài: Ôn tập chương 1

Câu 1: Trong một mặt phẳng, với phép biến hình f biến hình H thành hình H’. Khi đó

A. Mỗi hình H’ có ít nhất một hình H mà f(H) = H’

B. Mỗi hình H’ có không quá một hình H mà f(H) = H’

C. Mỗi hình H’ có chỉ một hình H mà f(H) = H’

D. Mỗi hình H’ có không phải một hình H mà f(H) = H’

Hiển thị đáp án  

Đáp án: C

Câu 2:  Cho tam giác ABC với G là trọng tâm, trực tâm H và tâm đường tròn ngoại tiếp. Gọi $A^{\text{'}},B^{\text{'}},C^{\text{'}}$ lần lượt là trung điểm các cạnh $BC,CA,AB$ của tam giác ABC. Hỏi qua phép biến hình nào thì điểm O biến thành điểm H ?

A. Phép vị tự tâm G , tỉ số -2 .

B. Phép quay tâm O , góc quay $60°$ . 

C. Phép tịnh tiến theo vectơ $\frac{1}{3}\overrightarrow{CA}$ .

D. Phép vị tự tâm G, tỉ số $\frac{1}{2}$ .

Hiển thị đáp án  

Đáp án: A

Giải thích:

 

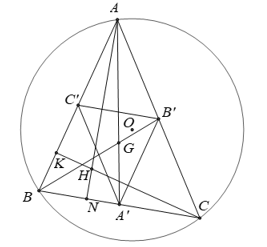
Ta có  $O{A}^{\text{'}}\perp BC,BC\parallel B^{\text{'}}{C}^{\text{'}}$$\Rightarrow O{A}^{\text{'}}\perp B^{\text{'}}{C}^{\text{'}}$ do đó ta có O chính là trực tâm của tam giác $A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}$.
Vì phép vị tự tâm G tỉ số -2 biến tam giác $A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}$ thành ABC nên sẽ biến trực tâm tam giác này thành tam giác kia, tức là O biến thành điểm H.

Câu 3: Trong mặt phẳng, với H là một hình (không phải một điểm) và phép biến hình f mà f(H) = H’. Khi đó

A. f(M) = M với mọi điểm M thuộc H

B. f(M) ≠ M với mọi điểm M thuộc H

C. f(M) ≠ M hoặc f(M) = M với điểm M thuộc H

D. f(M) = M với đúng một điểm M thuộc H

Hiển thị đáp án  

Đáp án: C

Câu 4: Trong mặt phẳng,

A. Nếu phép biến hình f biến hình H thành hình H thì f là phép đồng nhất

B. Nếu phép biến hình f biến điểm M thành điểm M thì f là phép đồng nhất

C. Nếu phép biến hình f biến một số điểm M thành chính nó thì f là phép đồng nhất

D. Nếu phép biến hình f biến mọi điểm M thành chính nó thì f là phép đồng nhất

Hiển thị đáp án  

Đáp án: D

Câu 5: Mệnh đề nào sau đây là sai ?

Trong mặt phẳng, có phép biến hình f

A. Biến mọi điểm M thành một điểm M’

B. Biến mọi điểm M thuộc đường thẳng d thành một điểm M’

C. Biến một điểm M thành hai điểm M’ và M’’ phân biệt

D. Biến hai điểm phân biệt M và M’ thành một điểm M’’

Hiển thị đáp án  

Đáp án: C

Câu 6: Cho hai điểm A,B phân biệt. Hãy chọn khẳng định sai trong các khẳng định sau đây:

A. Có duy nhất phép đối xứng trục biến điểm A  thành B.

B. Có duy nhất phép đối xứng tâm biến điểm A thành B.

C. Có duy nhất phép tịnh tiến biến điểm A thành  B.

D. Có duy nhất phép vị tự biến điểm A thành B.

Hiển thị đáp án  

Đáp án: D

Giải thích:

Có duy nhất phép đối xứng trục d biến điểm A thành B với d là trung trực AB (mỗi đoạn có duy nhất một trung trực)

Có duy nhất phép đối xứng tâm I biến điểm A thành B (AB có duy nhất một trung điểm I)

Có duy nhất phép tịnh tiến biến điểm A thành (vì $\overrightarrow{AB}$ là duy nhất với A, cố định cho trước)

Phép vị tự $V\left(I;k\right)\left(A\right)=B\Rightarrow \overrightarrow{IB}=k\overrightarrow{IA}$ do đó ứng với mỗi tâm vị tự I và một tỉ số k cho ta một phép vị tự, do đó có vô số phép vị tự.

Câu 7: Cho hai đường tròn tiếp xúc nhau ở A. Hãy chọn phát biểu sai trong các phát biểu sau:

A. Tiếp điểm A  là tâm vị tự trong của hai đường tròn.

B. Tiếp điểm  A là một trong hai tâm vị tự trong hoặc ngoài của hai đường tròn.

C. Nếu hai đường tròn đó tiếp xúc ngoài thì tiếp điểm A  là tâm vị tự trong.

D. Nếu hai đường tròn đó tiếp xúc trong thì tiếp điểm  A là tâm vị tự ngoài.

Hiển thị đáp án  

Đáp án: A

Giải thích:

Nếu hai đường tròn tiếp xúc trong với nhau thì phép vị tự tâm A, tỉ số  $k=\frac{R}{R^{\text{'}}}$ hoặc $k=\frac{R^{\text{'}}}{R}$  biến đường tròn này thành đường tròn kia.

Do đó  A chính là tâm vị tự ngoài. (Đáp án D đúng)

Câu 8: Cho hai đường tròn bằng nhau $\left(O;R\right)$ và $\left(O^{\text{'}};R\right)$. Có bao nhiêu phép vị tự biến đường tròn  $\left(O;R\right)$ thành $\left(O^{\text{'}};R\right)$ ?

A. Vô số.

B. 1 .

C. 2 .

D. Không có.

Hiển thị đáp án  

Đáp án: B

Giải thích:

Chỉ có duy nhất một phép vị tự là phép vị tự có tâm là trung điểm của $O{O}^{\text{'}}$ và tỉ số vị tự bằng -1 .

Câu 9: Tìm mệnh đề sai trong các mệnh đề sau:

A. Có một phép tịnh tiến biến mỗi điểm trong mặt phẳng thành chính nó.

B. Có một phép quay biến mỗi điểm trong mặt phẳng thành chính nó.

C. Có một phép vị tự biến mỗi điểm trong mặt phẳng thành chính nó.

D. Có một phép đối xứng trục biến mỗi điểm trong mặt phẳng thành chính nó.

Hiển thị đáp án  

Đáp án: D

Giải thích:

Chỉ có những điểm trên trục đối xứng mới biến thành chính nó.

Câu 10: Trong một mặt phẳng, với phép biến hình f biến hình H thành hình H’. Khi đó

A. Hình H’ có thể trùng với hình H

B. Hình H’ luôn luôn trùng với hình H

C. Hình H’ luôn là tập con của hình H

D. Hình H luôn là tập con của hình H’

Hiển thị đáp án  

Đáp án: A

Xem thêm các bài tổng hợp lý thuyết Toán lớp 11 đầy đủ, chi tiết khác:

Lý thuyết Đại cương về đường thẳng và mặt phẳng

Lý thuyết Hai đường thẳng chéo nhau và hai đường thẳng song song

Lý thuyết Đường thẳng và mặt phẳng song song

Lý thuyết Hai mặt phẳng song song

Lý thuyết Phép chiếu song song. Hình biểu diễn của một hình không gian