Lý thuyết Hai đường thẳng vuông góc (mới 2023 + Bài Tập) - Toán 11

Lý thuyết Toán 11 Bài 2: Hai đường thẳng vuông góc

Bài giảng Toán 11 Bài 2: Hai đường thẳng vuông góc

A. Lý thuyết.

I. Tích vô hướng của hai vecto trong không gian.

1. Góc giữa hai vecto trong không gian.

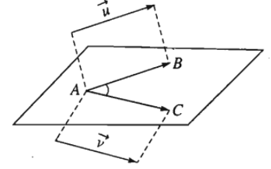
- Định nghĩa.  Trong không gian, cho $\overrightarrow{u};\overrightarrow{v}$ là hai vecto khác vecto- không. Lấy một điểm A bất kì, gọi B và C là hai điểm sao cho $\overrightarrow{AB}=\overrightarrow{u};\overrightarrow{AC}=\overrightarrow{v}$. Khi đó, ta gọi góc $\widehat{BAC}(0^0\le \widehat{BAC}\le {180}^0)$ là góc giữa hai vecto $\overrightarrow{u};\overrightarrow{v}$ trong không gian.

Kí hiệu là ($\overrightarrow{u};\overrightarrow{v}$).

2. Tích vô hướng của hai vecto trong không gian.

- Định nghĩa:

Trong không gian có hai vecto $\overrightarrow{u};\overrightarrow{v}$ đều khác vecto- không . Tích vô hướng của hai vecto là một số, kí hiệu là $\overrightarrow{u};\overrightarrow{v}$, được xác định bởi công thức: $\overrightarrow{u}.\overrightarrow{v}=\left|\overrightarrow{u}\right|.\left|\overrightarrow{v}\right|.c\text{os\hspace{0.17em}}\left(\overrightarrow{u};\overrightarrow{v}\right)$

Trường hợp $\overrightarrow{u}=\overrightarrow{0}$ hoặc $\overrightarrow{v}=\overrightarrow{0}$ ta quy ước: $\overrightarrow{u}.\overrightarrow{v}$ = 0.

Ví dụ 1. Cho hình chóp S.ABC có SA= SB= SC và $\widehat{A\text{}SB}=\widehat{BSC}=\widehat{CSA}$. Hãy xác định góc giữa cặp vectơ $\overrightarrow{SC}$ và $\overrightarrow{AB}$?

Lời giải :

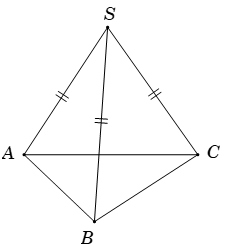
Ta có

$$\begin{gathered} \overrightarrow{\mathrm{SC}}.\overrightarrow{\mathrm{AB}}=\overrightarrow{\mathrm{SC}}.\left(\overrightarrow{\mathrm{SB}}-\overrightarrow{\mathrm{SA}}\right) \\ =\overrightarrow{\mathrm{SC}}.\overrightarrow{\mathrm{SB}}-\overrightarrow{\mathrm{SC}}.\overrightarrow{\mathrm{SA}} \\ \begin{array}{l}\\ =\left|\overrightarrow{\mathrm{SC}}\right|.\left|\overrightarrow{\mathrm{SB}}\right|.\cos \left(\overrightarrow{\mathrm{SC}}.\overrightarrow{\mathrm{SB}}\right)- \left|\overrightarrow{\mathrm{SC}}\right|.\left|\overrightarrow{\mathrm{SA}}\right|.\cos \left(\overrightarrow{\mathrm{SC}}.\overrightarrow{\mathrm{SA}}\right)\\ \\ =\mathrm{SC}.\mathrm{SB}.\cos \widehat{\mathrm{BSC}}- \mathrm{SC}.\mathrm{SA}.\cos \widehat{\mathrm{ASC}}\end{array} \end{gathered}$$

Vì SA= SB= SC và $\widehat{A\text{}SB}=\widehat{BSC}=\widehat{CSA}$$\Rightarrow \overrightarrow{SC}.\overrightarrow{AB}=0$

Ta lại có:

$$\begin{gathered} \overrightarrow{SC}.\overrightarrow{SA}=\left|\overrightarrow{SC}\right|.\left|\overrightarrow{SA}\right|.cos\left(\overrightarrow{SC},\overrightarrow{SA}\right) \\ \Rightarrow cos\left(\overrightarrow{SC},\overrightarrow{SA}\right)=0 \end{gathered}$$

Do đó $\left(\overrightarrow{SC};\overrightarrow{AB}\right)={90}^0$.

II. Vector chỉ phương của đường thẳng

1. Định nghĩa.

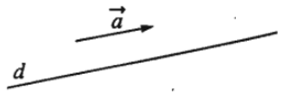
Nếu $\overrightarrow{a}$ khác vecto - không được gọi là vecto chỉ phương của đường thẳng d nếu giá của vecto $\overrightarrow{a}$ song song hoặc trùng với đường thẳng d.

2. Nhận xét.

a) Nếu $\overrightarrow{a}$ là vecto chỉ phương của đường thẳng d thì vecto $k\overrightarrow{a}(k\ne 0)$ cũng là vecto chỉ phương của d.

b) Một đường thẳng d trong không gian hoàn toàn được xác định nếu biết một điểm A thuộc đường thẳng d và một vecto chỉ phương của nó.

c) Hai đường thẳng song song với nhau khi và chỉ khi chúng là hai đường thẳng phân biệt và có hai vecto chỉ phương cùng phương.

III. Góc giữa hai đường thẳng trong không gian.

1. Định nghĩa:

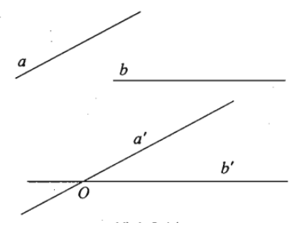
Góc giữa hai đường thẳng a và b trong không gian là góc giữa hai đường thẳng a’ và b’ cùng đi qua một điểm và lần lượt song song với a và b.

2. Nhận xét.

a) Để xác định góc giữa hai đường thẳng a và b ta có thể lấy điểm O thuộc một trong hai đường thẳng đó rồi vẽ một đường thẳng qua O và song song với đường thẳng còn lại.

b) Nếu $\overrightarrow{u}$ là vecto chỉ phương của đường thẳng a và là $\overrightarrow{v}$ vecto chỉ phương của đường thẳng b và $(\overrightarrow{u};\overrightarrow{v})=\alpha$ thì góc giữa hai đường thẳng a và b bằng  nếu $0^0\le \alpha \le {90}^0$ và bằng ${180}^0-\alpha$ nếu ${90}^0<\alpha \le {180}^0$.

Nếu a và b song song hoặc trùng nhau thì góc giữa chúng bằng 0⁰.

Ví dụ 2. Cho hình lập phương ABCD.A’B’C’D’.  Tính góc giữa AC và DA’

Lời giải:

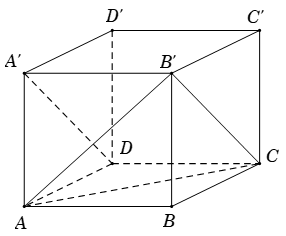
Gọi a là độ dài cạnh hình lập phương.

Khi đó, tam giác AB’C đều (AB’ = B’C= CA = $a\sqrt{2}$)

Do đó $\widehat{B\text{'}CA}={60}^0$.

Lại có, DA’ song song CB’  nên  

(AC ; DA’) = (AC ; CB’) = $\widehat{B\text{'}CA}={60}^0$.

IV. Hai đường thẳng vuông góc.

1. Định nghĩa.

Hai đường thẳng được gọi là vuông góc nếu góc giữa chúng bằng 90⁰.

Ta kí hiệu hai đường thẳng a và b vuông góc với nhau là $a\perp b$.

2. Nhận xét

a) Nếu $\overrightarrow{u};\overrightarrow{v}$ lần lượt là các vecto chỉ phương của hai đường thẳng a và b thì $a\perp b\iff \overrightarrow{u}.\overrightarrow{v}=0$.

b) Cho hai đường thẳng song song. Nếu một đường thẳng vuông góc với đường thẳng này thì cũng vuông góc với đường thẳng kia.

c) Hai đường thẳng vuông góc với nhau có thể cắt nhau hoặc chéo nhau.

Ví dụ 3.  Cho tứ diện ABCD có AB= AC= AD  và $\widehat{BAC}=\widehat{BAD}={60}^0;\widehat{CAD}={90}^0$. Gọi I và J lần lượt là trung điểm của AB  và CD. Chứng minh hai đường thẳng AB và IJ vuông góc với nhau.

Lời giải:

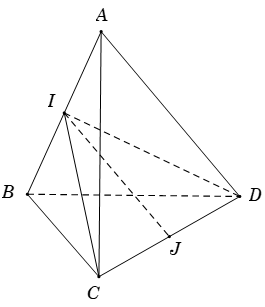
Xét tam giác ICD có J là trung điểm đoạn CD  $\Rightarrow \overrightarrow{I\text{}J}=\frac{1}{2}\left(\overrightarrow{IC}+\overrightarrow{ID}\right).$

Tam giác ABC có AB = AC và $\widehat{BAC}={60}^0$ nên tam giác ABC đều

$\Rightarrow CI\perp AB$.  (1)

Tương tự, ta có tam giác ABD  đều nên $DI\perp AB$.  ( 2)

Từ  (1) và (2) ta có :

$$\begin{gathered} \overrightarrow{IJ}.\overrightarrow{AB}=\frac{1}{2}\left(\overrightarrow{IC}+\overrightarrow{ID}\right).\overrightarrow{AB} \\ =\frac{1}{2}\overrightarrow{IC}.\overrightarrow{AB}+\frac{1}{2}\overrightarrow{ID}.\overrightarrow{AB}=0 \\ \Rightarrow \overrightarrow{\text{IJ}}\perp \overrightarrow{AB}\Rightarrow \text{IJ}\perp \text{}AB \end{gathered}$$

B. Bài tập tự luyện

Bài 1. Cho tứ diện ABCD có AB = CD = a, $IJ=\frac{a\sqrt{3}}{2}$ ( I; J lần lượt là trung điểm của BC và AD). Tính số đo góc giữa hai đường thẳng AB và CD:

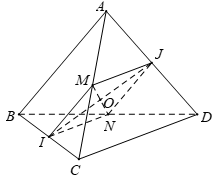
Gọi M; N  lần lượt là trung điểm AC; BD.

Ta có:

$\left\{\begin{array}{l}MI=NI=\frac{1}{2}AB=\frac{1}{2}CD=\frac{a}{2}\\ MI\text{ // }AB\text{ // }CD\text{ // }NI\end{array}\right.$ $\Rightarrow MINJ$ là hình thoi.

Gọi O là giao điểm của MN và IJ.

Ta có: $\widehat{MIN}=2\widehat{MIO}$.

Xét tam giác MIO vuông tại O, ta có:

$$\begin{gathered} \cos \widehat{MIO}=\frac{IO}{MI}=\frac{\frac{a\sqrt{3}}{4}}{\frac{a}{2}}=\frac{\sqrt{3}}{2} \\ \Rightarrow \widehat{MIO}=30°\Rightarrow \widehat{MIN}=60° \end{gathered}$$

Mà: $\left(AB,CD\right)=\left(IM,IN\right)=\widehat{MIN}=60°$

Bài 2. Cho tứ diện ABCD có BA = CD. Gọi  I ; J ; E ; F lần lượt là trung điểm của AC ; BC ; BD ; AD. Tính góc ( IE ; JF) 

Lời giải :

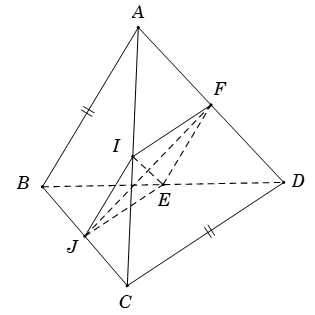
Ta có IF là đường trung bình của tam giác ACD $\Rightarrow \left\{\begin{array}{l}IF\parallel CD\\ IF=\frac{1}{2}CD\end{array}\right.$  ( 1)

Lại có JE là đường trung bình của tam giác BCD  $\Rightarrow \left\{\begin{array}{l}JE\parallel CD\\ JE=\frac{1}{2}CD\end{array}\right.$ ( 2)

Từ (1)  và (2) suy ra : IF = JE và IF// JE.

Suy ra, tứ giác IJEF là hình bình hành.

Mặt khác: $\left\{\begin{array}{l}IJ=\frac{1}{2}AB\\ JE=\frac{1}{2}CD\end{array}\right.$. Mà AB= CD nên IJ= JE.

Do đó IJEF  là hình thoi.

Suy ra ( IE ; JF) = 90⁰.

Bài 3. Cho tứ diện đều ABCD. Số đo góc giữa hai đường thẳng AB và CD  bằng:

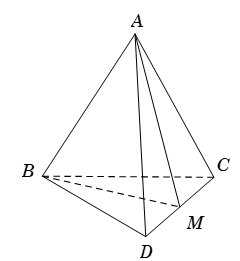
Lời giải :

Gọi M là trung điểm của CD.

Tam giác ACD  và tam giác BCD  là  tam giác đều ( vì ABCD là tứ diện đều) có AM ; BM là hai đường trung  tuyến ứng với cạnh CD nên đồng thời là đường cao. $\Rightarrow \overrightarrow{CD}.\overrightarrow{AM}=0;\overrightarrow{CD}.\overrightarrow{MB}=0;$

Do đó $\overrightarrow{CD}.\overrightarrow{AB}=\overrightarrow{CD}.\left(\overrightarrow{AM}+\overrightarrow{MB}\right)$ $=\overrightarrow{CD}.\overrightarrow{AM}+\overrightarrow{CD}.\overrightarrow{MB}=0$.

Suy ra $\overrightarrow{AB}\perp \overrightarrow{CD}$ nên số đo góc giữa hai đường thẳng AB và CD  bằng 90⁰

Trắc nghiệm Toán 11 Bài 2: Hai đường thẳng vuông góc

Câu 1: Cho tứ diện có ABCD, $AB=CD=a$, $IJ=\frac{a\sqrt{3}}{2}$ (I,J lần lượt là trung điểm của BC và AD). Số đo góc giữa hai đường thẳng AB và CD là

A. $30°$

B. $45°$

C. $60°$

D. $90°$

Hiển thị đáp án  

Đáp án: C

Giải thích:

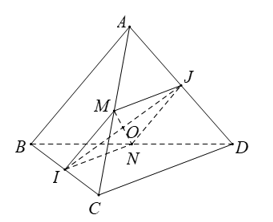
Gọi M, N lần lượt là trung điểm AC, BC.

Ta có: 

$\left\{\begin{array}{l}MI=NI=\frac{1}{2}AB=\frac{1}{2}CD=\frac{a}{2}\\ MI\text{ // }AB\text{ // }CD\text{ // }NI\end{array}\right.$

$\Rightarrow MINJ$ là hình thoi.

Gọi O là giao điểm của MN và IJ.

Ta có: $\widehat{MIN}=2\widehat{MIO}$.

Xét $\Delta MIO$ vuông tại O , ta có:

$\cos \widehat{MIO}=\frac{IO}{MI}=\frac{\frac{a\sqrt{3}}{4}}{\frac{a}{2}}=\frac{\sqrt{3}}{2}$

$\Rightarrow \widehat{MIO}=30°\Rightarrow \widehat{MIN}=60°$

Mà: $\left(AB,CD\right)=\left(IM,IN\right)=\widehat{MIN}=60°$.

Câu 2: Cho hình hộp $ABCD.A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}{D}^{\text{'}}$. Giả sử tam giác $A{B}^{\text{'}}C$ và $A^{\text{'}}D{C}^{\text{'}}$ đều có 3 góc nhọn. Góc giữa hai đường thẳng $AC$ và $A^{\text{'}}D$ là góc nào sau đây?

A. $\widehat{BD{B}^{\text{'}}}$

B. $\widehat{A{B}^{\text{'}}C}$

C. $\widehat{D{B}^{\text{'}}B}$

D. $\widehat{D{A}^{\text{'}}{C}^{\text{'}}}$

Hiển thị đáp án  

Đáp án: D

Giải thích:

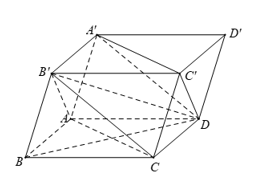
Ta có: $AC\text{ // }{A}^{\text{'}}{C}^{\text{'}}$ (tính chất của hình hộp)

$\Rightarrow \left(AC,A^{\text{'}}D\right)=\left(A^{\text{'}}{C}^{\text{'}},A^{\text{'}}D\right)=\widehat{D{A}^{\text{'}}{C}^{\text{'}}}$

(do giả thiết cho $\Delta D{A}^{\text{'}}{C}^{\text{'}}$nhọn).

Câu 3: Cho tứ diện đều ABCD (Tứ diện có tất cả các cạnh bằng nhau). Số đo góc giữa hai đường thẳng AB và CD bằng

A. $30°$

B. $45°$

C. $60°$

D. $90°$

Hiển thị đáp án  

Đáp án: D

Giải thích:

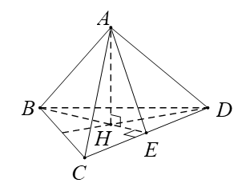
Gọi H là tâm đường tròn ngoại tiếp $\Delta BCD\Rightarrow AH\perp \left(BCD\right)$.

Gọi E là trung điểm CD $\Rightarrow BE\perp CD$ (do $\Delta BCD$ đều).

Do $AH\perp \left(BCD\right)\Rightarrow AH\perp CD$.

Ta có: $\left\{\begin{array}{l}CD\perp BE\\ CD\perp AH\end{array}\right.\Rightarrow CD\perp \left(ABE\right)$

$\Rightarrow CD\perp AB\Rightarrow \widehat{\left(AB,CD\right)}=90°$

Câu 4: Cho hình chóp S.ABCD có đáy là hình vuông ABCD cạnh bằng a và các cạnh bên đều bằng a. Gọi M và N lần lượt là trung điểm của AD và SD. Số đo của góc bằng $\left(MN,SC\right)$

A. $30°$

B.  $45°$

C. $60°$

D. $90°$

Hiển thị đáp án  

Đáp án: D

Giải thích:

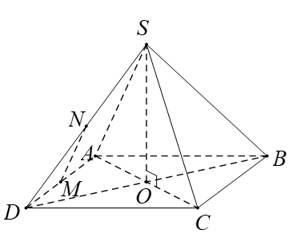
Gọi O là tâm của hình vuông ABCD $\Rightarrow O$ là tâm đường tròn ngoại tiếp của hình vuông ABCD(1).

Ta có: $SA=SB=SC=SD$

$\Rightarrow S$ nằm trên trục của đường tròn ngoại tiếp hình vuông ABCD (2).

Từ (1) và (2) $\Rightarrow SO\perp \left(ABCD\right)$

Từ giả thiết ta có: $MN\text{ // }SA$ (do MN là đường trung bình của $\Delta SAD$). 

$\Rightarrow \left(MN,SC\right)=\left(SA,SC\right)$

Xét $\Delta SAC$, ta có:

$\left\{\begin{array}{l}S{A}^2+S{C}^2=a^2+a^2=2a^2\\ A{C}^2=2AD=2a^2\end{array}\right.$

$\Rightarrow \Delta SAC$ vuông tại S $\Rightarrow SA\perp SC$

$\Rightarrow \left(SA,SC\right)=\left(MN,SC\right)=90°$.

Câu 5: Trong không gian cho ba đường thẳng phân biệt a, b, c. Khẳng định nào sau đây đúng?

A. Nếu a và b cùng vuông góc với c thì $a\text{\hspace{0.17em}\hspace{0.17em}//\hspace{0.17em}}b$.

B. Nếu $a\text{\hspace{0.17em}\hspace{0.17em}//\hspace{0.17em}}b$ và $c\perp a$ thì $c\perp b$.

C. Nếu góc giữa a và c bằng góc giữa b và c thì $a\text{\hspace{0.17em}\hspace{0.17em}//\hspace{0.17em}}b$.

D. Nếu a và b cùng nằm trong mp$\left(\alpha \right)\text{\hspace{0.17em}\hspace{0.17em}//\hspace{0.17em}}c$ thì góc giữa a và c bằng góc giữa b và c.

Hiển thị đáp án  

Đáp án: B

Giải thích:

Nếu a và b cùng vuông góc với c thì a và b hoặc song song hoặc chéo nhau.

C sai do:

Giả sử hai đường thẳng a và b chéo nhau, ta dựng đường thẳng c là đường vuông góc chung của a và b . Khi đó góc giữa a và c bằng với góc giữa b và c và cùng bằng $90°$, nhưng hiển nhiên hai đường thẳng a và b không song song.

D sai do: giả sử a vuông góc với c, b song song với c , khi đó góc giữa a và c bằng $90°$, còn góc giữa b và c bằng $0°$.

Do đó B đúng.

Câu 6: Trong các mệnh đề sau mệnh đề nào đúng?

A. Góc giữa hai đường thẳng a và b bằng góc giữa hai đường thẳng a và c khi b song song với c (hoặc b trùng với c).

B. Góc giữa hai đường thẳng a và b bằng góc giữa hai đường thẳng a và c thì b song song với c

C. Góc giữa hai đường thẳng là góc nhọn.

D. Góc giữa hai đường thẳng bằng góc giữa hai véctơ chỉ phương của hai đường thẳng đó.

Hiển thị đáp án  

Đáp án: A

Câu 7: Cho tứ diện ABCD có hai cặp cạnh đối vuông góc. Trong các mệnh đề sau mệnh đề nào đúng?

A. Tứ diện có ít nhất một mặt là tam giác nhọn.

B. Tứ diện có ít nhất hai mặt là tam giác nhọn.

C. Tứ diện có ít nhất ba mặt là tam giác nhọn.

D. Tứ diện có cả bốn mặt là tam giác nhọn.

Hiển thị đáp án  

Đáp án: A

Câu 8: Trong các mệnh đề dưới đây mệnh đề đúng là?

A. Cho hai đường thẳng song song, đường thẳng nào vuông góc với đường thẳng thứ nhất thì cũng vuông góc với đường thẳng thứ hai.

B. Trong không gian, hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì song song với nhau.

C. Hai đường thẳng phân biệt vuông góc với nhau thì chúng cắt nhau.

D. Hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì vuông góc với nhau.

Hiển thị đáp án  

Đáp án: A

Giải thích:

Theo lý thuyết.

Câu 9: Trong các mệnh đề sau đây, mệnh đề nào là đúng?

A. Nếu đường thẳng a vuông góc với đường thẳng b và đường thẳng b vuông góc với đường thẳng c thì a vuông góc với c

B. Cho ba đường thẳng $a,b,c$ vuông góc với nhau từng đôi một. Nếu có một đường thẳng SA vuông góc với a thì d song song với b hoặc c.

C. Nếu đường thẳng O vuông góc với đường thẳng b và đường thẳng b song song với đường thẳng BD thì a vuông góc với c

D. Cho hai đường thẳng a và b song song với nhau. Một đường thẳng c vuông góc với a thì c vuông góc với mọi đường thẳng nằm trong mặt phẳng $\left(a,b\right)$.

Hiển thị đáp án  

Đáp án: C

Câu 10: Trong các mệnh đề sau đây, mệnh đề nào là đúng?

A. Một đường thẳng cắt hai đường thẳng cho trước thì cả ba đường thẳng đó cùng nằm trong một mặt phẳng

B. Ba đường thẳng cắt nhau từng đôi một và không nằm trong một mặt phẳng thì đồng quy

C. Một đường thẳng cắt hai đường thẳng cắt nhau cho trước thì cả ba đường thẳng đó cùng nằm trong một mặt phẳng

D. Ba đường thẳng cắt nhau từng đôi một thì cùng nằm trong một mặt phẳng

Hiển thị đáp án  

Đáp án: B

Giải thích:

Gọi $d_1$,$d_2$,$d_3$ là 3 đường thẳng cắt nhau từng đôi một. Giả sử $d_1$, $d_2$ cắt nhau tại A, vì $d_3$ không nằm cùng mặt phẳng với $d_1,d_2$ mà $d_3$ cắt $d_1,d_2$, nên $d_3$ phải đi qua A. Thật vậy giả sử $d_3$ không đi qua A thì nó phải cắt $d_1,d_2$ tại hai điểm B,C điều này là vô lí, một đường thẳng không thể cắt một mặt phẳng tại hai điểm phân biệt.

Xem thêm các bài tổng hợp lý thuyết Toán lớp 11 đầy đủ, chi tiết khác:

Lý thuyết Vectơ trong không gian

Lý thuyết Đường thẳng vuông góc với mặt phẳng 

Lý thuyết Hai mặt phẳng vuông góc 

Lý thuyết Khoảng cách 

Lý thuyết Ôn tập chương 5