Nội dung bài viết

    Xem thêm

    Lý thuyết Phép nhân đa thức – Toán lớp 8 Kết nối tri thức

    Với lý thuyết Toán lớp 8 Bài 4: Phép nhân đa thức chi tiết, ngắn gọn và bài tập tự luyện có lời giải chi tiết sách Kết nối tri thức sẽ giúp học sinh nắm vững kiến thức trọng tâm để học tốt môn Toán 8.

    1 1,712 07/12/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Lý thuyết Toán 8 Bài 4: Phép nhân đa thức - Kết nối tri thức

    Bài giảng Toán 8 Bài 4: Phép nhân đa thức - Kết nối tri thức

    A. Lý thuyết Phép nhân đa thức

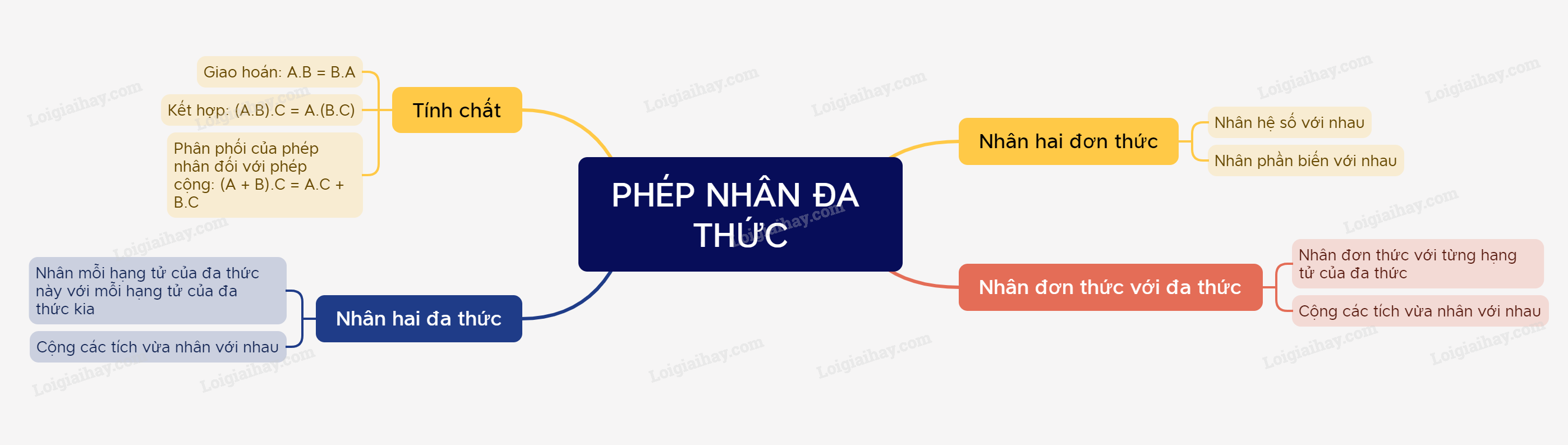
    1. Nhân đơn thức với đa thức

    + Nhân hai đơn thức như thế nào?

    Muốn nhân hai đơn thức, ta nhân hai hệ số với nhau và nhân hai phần biến với nhau.

    Ví dụ: (−3x2y)(4xy)=[(−3.4)].(x2.x).(y.y)=−12.x3.y2

    + Nhân đơn thức với đa thức như thế nào?

    Muốn nhân một đơn thức với một đa thức, ta nhân đơn thức với từng hạng tử của đa thức rồi cộng các tích với nhau.

    Ví dụ:

    3x2y(2x2y−xy+3y2)=(3x2y).(2x2y)−(3x2y).(xy)+(3x2y).(3y2)=3.2.(x2.x2)(y.y)−3.(x2.x).(y.y)+3.3.x2.(y.y2)=6x4y2−3x3.y2+9x2y3

    2. Nhân đa thức với đa thức

    + Nhân hai đa thức như thế nào?

    Muốn nhân một đa thức với một đa thức, ta nhân mỗi hạng tử của đa thức này với từng hạng tử của đa thức kia rồi cộng các tích với nhau.

    Phép nhân đa thức cũng có các tính chất tương tự phép nhân các số.

    + Giao hoán: A.B = B.A

    + Kết hợp: (A.B).C = A.(B.C)

    + Phân phối của phép nhân đối với phép cộng: (A + B).C = AB + AC

    Ví dụ:

    (xy+1)(xy−3)=(xy).(xy)+xy−3xy−3=x2y2−2xy−3

    B. Bài tập Phép nhân đa thức

    Bài 1. Làm tính nhân:

    a) (x2 – xy + y2)(xy + 2);

    b) (x – 2y)(x2 + 2xy + 4y2).

    Hướng dẫn giải

    a) (x2 – xy + y2)(xy + 2) = (x2 – xy + y2).xy + (x2 – xy + y2).2

    = x3y – x2y2 + xy3 + 2x2 – 2xy + 2y2.

    b) (x – 2y)(x2 + 2xy + 4y2) = x. (x2 + 2xy + 4y2) + (– 2y) (x2 + 2xy + 4y2)

    = x3 + 2x2y + 4xy2 – 2x2y – 4xy2 – 8y3

    = x3 + (2x2y – 2x2y) + (4xy2 – 4xy2) – 8y3

    = x3 – 8y3.

    Bài 2. Chứng minh giá trị của biểu thức sau không phụ thuộc vào giá trị của biến:

    (2x + 2022).(1 – x2) + x(2x2 – 2 + 2022x).

    Hướng dẫn giải

    Ta có: (2x + 2022).(1 – x2) + x(2x2 – 2 + 2022x)

    = 2x.(1 – x2) + 2022.(1 – x2) + 2x3 – 2x + 2022x2

    = 2x – 2x3 + 2022 – 2022x2 + 2x3 – 2x + 2022x2

    = (2x – 2x) + (– 2x3 + 2x3) + (– 2022x2 + 2022x2) + 2022

    = 0 + 0 + 0 + 2022

    = 2022 với mọi giá trị của x.

    Vậy giá trị của biểu thức (2x + 2022).(1 – x2) + x(2x2 – 2 + 2022x) không phụ thuộc vào giá trị của biến.

    Bài 3. Nhân hai đơn thức:

    a) 2xy2 và – 3x2y;

    b) −25x4y3 và 10xy;

    c) 0,5xyz và 4x3y2z.

    Hướng dẫn giải

    a) (2xy2).(– 3x2y) = 2.( – 3).(xy2).(x2y) = – 6x3y3

    b) ( −25x4y3).(10xy) = −25 .10.( x4y3).(xy) = – 4x5y4

    c) (0,5xyz).(4x3y2z) = 0,5.4.(xyz).( x3y2z) = 2x4y3z2.

    Bài 4. Tìm tích của đơn thức với đa thức:

    a) – x3(5xy – y3 + 2xy2);

    b) (x2y2 −12 x2y + 56 xy2).12xy.

    Hướng dẫn giải

    a) – x3(5xy – y3 + 2xy2) = (– x3).5xy + (– x3).( – y3) + (– x3).(2xy2)

    = – 5x4y + x3y3 – 2x4y2.

    b) (x2y2 −12 x2y + 56 xy2).12xy = x2y2.12xy + ( −12x2y).12xy + 56 xy2.12xy

    = 12x3y3 – 6x3y2 + 10x2y3.

    Xem thêm tóm tắt lý thuyết Toán lớp 8 sách Kết nối tri thức hay, chi tiết khác:

    Lý thuyết Bài 5: Phép chia đa thức cho đơn thức

    Lý thuyết Bài 6: Hiệu hai bình phương. Bình phương của một tổng hay một hiệu

    Lý thuyết Bài 7: Lập phương của một tổng. Lập phương của một hiệu

    Lý thuyết Bài 8: Tổng và hiệu hai lập phương

    Lý thuyết Bài 9: Phân tích đa thức thành nhân tử

    Tham khảo các loạt bài Toán 8 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 1,712 07/12/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: