Nội dung bài viết

    Xem thêm

    Lý thuyết Đường trung bình của tam giác (chính xác nhất) và cách giải các dạng bài tập

    Với lý thuyết Toán lớp 8 Bài 16: Đường trung bình của tam giác chi tiết, ngắn gọn và bài tập tự luyện có lời giải chi tiết sách Kết nối tri thức sẽ giúp học sinh nắm vững kiến thức trọng tâm để học tốt môn Toán 8.

    1 3,466 04/09/2024
    Trang trước
    Chia sẻ
    Trang sau  

    Lý thuyết Đường trung bình của tam giác (chính xác nhất) và cách giải các dạng bài tập

    Đường trung bình của tam giác là gì ? Công thức đường trung bình của tam giác

    I. Lý thuyết Đường trung bình của tam giác

    1. Đường trung bình của tam giác là gì?

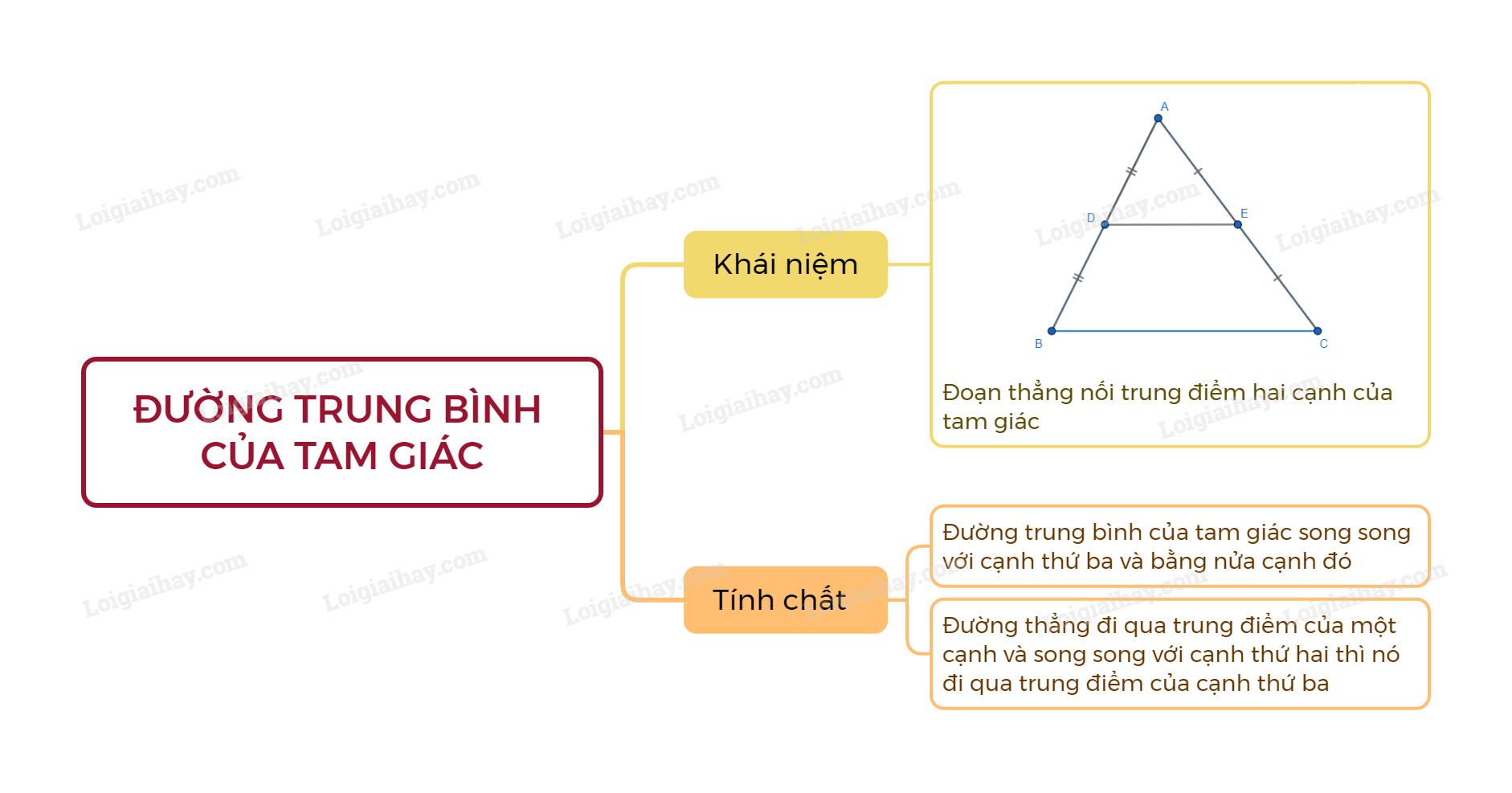
    Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác.

    2. Tính chất đường trung bình của tam giác

    Đường trung bình của tam giác song song với cạnh thứ ba và bằng nửa cạnh đó.

    Chú ý: Trong một tam giác, nếu một đường thẳng đi qua trung điểm của một cạnh và song song với cạnh thứ hai thì nó đi qua trung điểm của cạnh thứ ba.

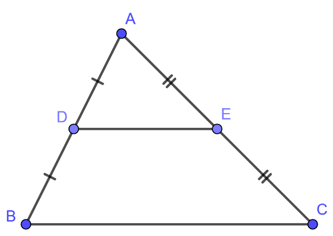
    Ví dụ:

    Đường trung bình của tam giác là gì ? Công thức đường trung bình của tam giác

    DE là đường trung bình của tam giác ABC, khi đó DE // BC và DE=12BC.

    II. Các dạng bài tập đường trung bình

    Dạng 1: Chứng minh các hệ thức về cạnh và góc. Tính các cạnh và góc.

    Phương pháp:

    Sử dụng tính chất đường trung bình của tam giác và hình thang.

    + Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy.

    + Đường trung bình của hình thang thì song song với hai đáy và bằng nửa tổng hai đáy.

    + Đường thẳng đi qua trung điểm một cạnh của tam giác và song song với cạnh thứ hai thì đi qua trung điểm cạnh thứ ba.

    + Đường thẳng đi qua trung điểm một cạnh bên của hình thang và song song với hai đáy thì đi qua trung điểm cạnh bên thứ hai.

    Dạng 2: Chứng minh một cạnh là đường trung bình của tam giác.

    Phương pháp:

    Sử dụng định nghĩa đường trung bình của tam giác và hình thang.

    + Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác.

    + Đường trung bình của hình thang là đoạn thẳng nối trung điểm hai cạnh bên của hình thang.

    III. Bài tập Đường trung bình của tam giác

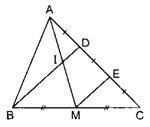
    Bài 1: Cho tam giác ABC, điểm D thuộc cạnh AC sao cho AD = 12 DC. Gọi M là trung điểm của BC, I là giao điểm của BD và AM. Chứng minh: AI = IM.

    Hướng dẫn giải

    Lý thuyết Toán 8 Kết nối tri thức Bài 16: Đường trung bình của tam giác

    Gọi E là trung điểm của DC.

    Trong ΔBDC, ta có:

    M là trung điểm của BC (giả thiết).

    E là trung điểm của CD (ta gọi).

    Nên ME là đường trung bình của ∆BCD.

    ⇒ ME // BD (tính chất đường trung bình tam giác).

    Suy ra: DI // ME.

    Lại có: AD = 12 DC (giả thiết).

    DE = 12 DC (vì E là trung điểm của DC).

    Suy ra AD = DE nên D là trung điểm của AE.

    Xét tam giác AME có D là trung điểm của AE và DI // ME (cmt).

    Suy ra I là trung điểm của AM (tính chất đường trung bình của tam giác)

    Vậy AI = IM.

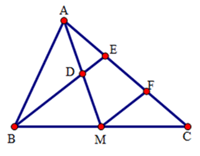
    Bài 2: Cho tam giác ABC, đường trung tuyến AM. Gọi D là trung điểm của AM, E là giao điểm của BD và AC, F là trung điểm của EC. Tính tỉ số AEEC .

    Hướng dẫn giải

    Lý thuyết Toán 8 Kết nối tri thức Bài 16: Đường trung bình của tam giác

    Xét ∆BEC có:

    M là trung điểm của BC;

    F là trung điểm của EC.

    Do đó, MF là đường trung bình của ∆BEC.

    Suy ra MF // BE.

    Xét ∆AMF có:

    D là trung điểm của AM;

    DE // MF (do MF // BE).

    Do đó, DE là đường trung bình của ∆AMF.

    Suy ra E là trung điểm của AF nên AE = EF.

    Mà EF = FC = 12 EC (do F là trung điểm của EC)

    Do vậy, AE = EF = FC = 12 EC.

    Suy ra AEEC  =  12 .

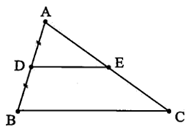
    Bài 3: Tính độ dài đoạn AE, biết DE // BC và AC = 8 cm.

    Lý thuyết Toán 8 Kết nối tri thức Bài 16: Đường trung bình của tam giác

    Hướng dẫn giải

    Xét tam giác ABC, ta có: D là trung điểm AB và DE // BC

    ⇒ E là trung điểm của AC.

    Suy ra: AE = 12AC  =  12⋅ 8  =  4 cm .

    Xem thêm tóm tắt lý thuyết Toán lớp 8 sách Kết nối tri thức hay, chi tiết khác:

    Lý thuyết Bài 17: Tính chất đường phân giác của tam giác

    Lý thuyết Bài 18: Thu thập và phân loại dữ liệu

    Lý thuyết Bài 19: Biểu diễn dữ liệu bằng bảng, biểu đồ

    Lý thuyết Bài 20: Phân tích số liệu thống kê dựa vào biểu đồ

    Lý thuyết Bài 21: Phân thức đại số

    Tham khảo các loạt bài Toán 8 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 3,466 04/09/2024
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: