Nội dung bài viết

    Xem thêm

    Lý thuyết Hình thang cân. Công thức tính chu vi, diện tích hình thang cân (2024) chính xác nhất

    Với lý thuyết Toán lớp 8 Bài 11: Hình thang cân chi tiết, ngắn gọn và bài tập tự luyện có lời giải chi tiết sách Kết nối tri thức sẽ giúp học sinh nắm vững kiến thức trọng tâm để học tốt môn Toán 8.

    1 2,998 27/08/2024
    Trang trước
    Chia sẻ
    Trang sau  

    Lý thuyết Hình thang cân. Công thức tính chu vi, diện tích hình thang cân

    Bài giảng Toán 8 Bài 11: Hình thang cân - Kết nối tri thức

    I. Lý thuyết Hình thang cân

    1. Khái niệm hình thang

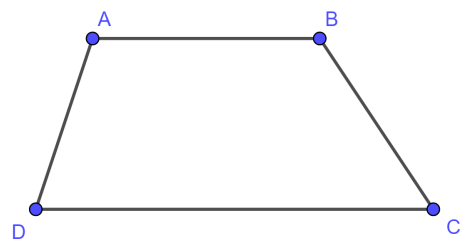
    Hình thang là tứ giác có hai cạnh đối song song.

    Hình thang là gì ? Định nghĩa, Tính chất về Hình thang chi tiết

    Minh họa:

    Lý thuyết Hình thang cân. Công thức tính chu vi, diện tích hình thang cân (2024) chính xác nhất (ảnh 1)

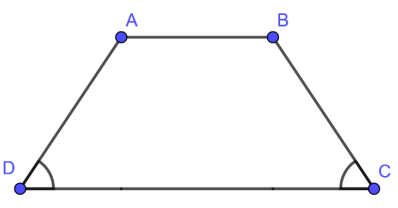
    2. Khái niệm hình thang cân

    Hình thang cân là hình thang có hai góc kề một đáy bằng nhau.

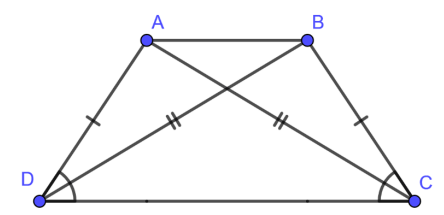
    \Hình thang cân là gì ? Định nghĩa, Tính chất về Hình thang cân chi tiết

    3. Tính chất của hình thang cân

    Hình thang cân là gì ? Định nghĩa, Tính chất về Hình thang cân chi tiết

    Trong hình thang cân,

    - Hai cạnh bên bằng nhau.

    - Hai đường chéo bằng nhau.

    4. Dấu hiệu nhận biết hình thang cân

    - Hình thang có hai góc kề một đáy bằng nhau là hình thang cân.

    - Nếu một hình thang có hai đường chéo bằng nhau thì hình thang đó là hình thang cân.

    Ví dụ:

    (ảnh 3)

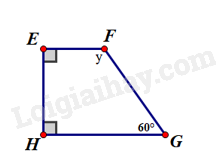
    Theo định lí về tổng các góc của một tứ giác, ta có E^+F^+G^+H^=3600. Do đó F^=y=3600−900−900−600=1200

    Vậy F^=1200

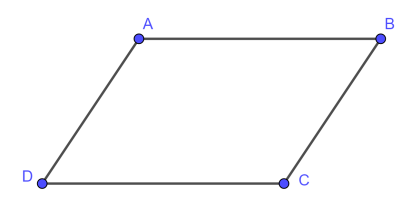
    Lưu ý: Hình thang cân thì có hai cạnh bên bằng nhau nhưng hình thang có hai cạnh bên bằng nhau chưa chắc đã là hình thang cân. Ví dụ như hình vẽ dưới đây:

    Hình thang cân là gì ? Định nghĩa, Tính chất về Hình thang cân chi tiết

    II. Công thức tính chu vi, diện tích hình thang

    - Công thức tính chu vi hình thang: bằng tổng độ dài của 2 đáy và 2 cạnh bên

    P = a + b + c + d

    - Công thức tính diện tích hình thang: bằng trung bình cộng 2 đáy nhân với chiều cao

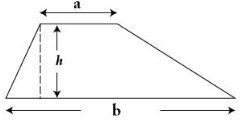
    Lý thuyết Hình thang cân. Công thức tính chu vi, diện tích hình thang cân (2024) chính xác nhất (ảnh 1)

    S = a + b2.h

    Muốn tính diện tích hình thang

    Đáy lớn đáy nhỏ ta đem cộng vào

    Cộng vào nhân với chiều cao

    Chia đôi lấy nửa thế nào cũng ra

    * Cách tính diện tích hình thang cân

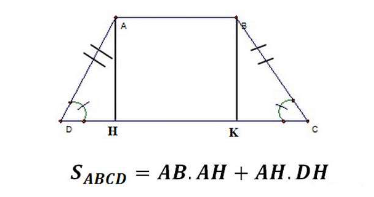
    Lý thuyết Hình thang cân. Công thức tính chu vi, diện tích hình thang cân (2024) chính xác nhất (ảnh 1)

    III. Bài tập Hình thang cân

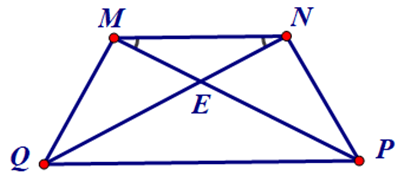
    Bài 1. Cho hình thang MNPQ (MN // PQ) có NMP^=MNQ^, E là giao điểm của MP và NQ. Chứng minh hình thang MNPQ là hình thang cân.

    Lý thuyết Toán 8 Kết nối tri thức Bài 11: Hình thang cân

    Hướng dẫn giải

    Vì MN // QP nên NMP^=MPQ^ và NQP^=MNQ^(các cặp góc so le trong)

    Mà NMP^=MNQ^⇒NMP^=MPQ^=NQP^=MNQ^.

    ΔMNE có NMP^=MNQ^ nên ΔMNEcân tại E

    Suy ra ME = NE (1)

    ΔQEP có MPQ^=NQP^ nên ΔQEP cân tại E

    Suy ra EQ = EP (2)

    Từ (1) và (2) ta có: ME + EP = NE + EQ hay MP = NQ

    Suy ra MNPQ là hình thang cân (dấu hiệu nhận biết).

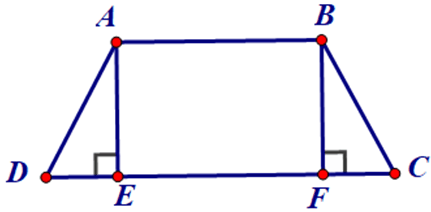
    Bài 2. Cho hình thang cân ABCD (AB // CD) có các đường cao AE, BF. Chứng minh DE = CF.

    Hướng dẫn giải

    Lý thuyết Toán 8 Kết nối tri thức Bài 11: Hình thang cân

    Vì ABCD (AB // CD) là hình thang cân nên D^=C^ và AD = BC.

    Xét ΔAED và ΔBFC có:

    AED^=BFC^=90° (AE⊥DC, BF⊥DC)

    D^=C^(chứng minh trên)

    AD = BC (chứng minh trên)

    Do đó ΔAED=ΔBFC (cạnh huyền - góc nhọn)

    Suy ra DE = CF (cạnh tương ứng bằng nhau).

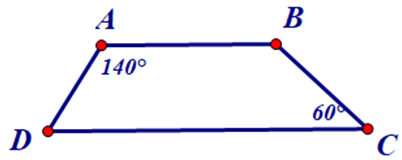
    Bài 3. Hình thang ABCD (AB // CD) trong hình bên dưới có phải hình thang cân không? Vì sao?

    Lý thuyết Toán 8 Kết nối tri thức Bài 11: Hình thang cân

    Hướng dẫn giải

    Giả sử ABCD (AB // CD) là hình thang cân.

    Khi đó, ta có: A^=B^=140°, C^=D^=60°.

    Tổng 4 góc trong hình thang ABCD là A^+B^+C^+D^=400°>360° .

    Suy ra ABCD không phải là hình thang cân.

    Xem thêm tóm tắt lý thuyết Toán lớp 8 sách Kết nối tri thức hay, chi tiết khác:

    Lý thuyết Bài 12: Hình bình hành

    Lý thuyết Bài 13: Hình chữ nhật

    Lý thuyết Bài 14: Hình thoi và hình vuông

    Lý thuyết Bài 15: Định lí Thalès trong tam giác

    Lý thuyết Bài 16: Đường trung bình của tam giác

    Tham khảo các loạt bài Toán 8 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 2,998 27/08/2024
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: