Giải Toán 10 trang 73 Tập 1 Chân trời sáng tạo
Với giải bài tập Toán lớp 10 trang 73 Tập 1 trong Bài 2: Định lí côsin và định lí sin sách Chân trời sáng tạo hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 10 trang 73 Tập 1.
Giải Toán 10 trang 73 Tập 1
Bài 4 trang 73 Toán lớp 10 Tập 1: Một công viên có dạng hình tam giác với các kích thước như Hình 15. Tính số đo các góc của tam giác đó.
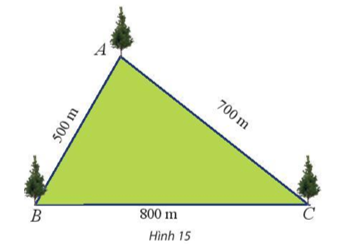
Lời giải:
Áp dụng hệ quả của định lí côsin ta có:
Vậy .
Bài 5 trang 73 Toán lớp 10 Tập 1: Tính diện tích một lá cờ hình tam giác cân có độ dài cạnh bên là 90 cm và góc ở đỉnh là 35°.

Lời giải:
Vì lá cờ hình tam giác cân nên độ dài hai cạnh bên bằng nhau và bằng 90cm.
Áp dụng công thức tính diện tích tam giác ta được
Vậy diện tích lá cờ là 2322,98 cm2.
Bài 6 trang 73 Toán lớp 10 Tập 1: Cho tam giác ABC có AB = 6, AC = 8 và .
a) Tính diện tích tam giác ABC.
b) Gọi I là tâm đường tròn ngoại tiếp tam giác ABC. Tính diện tích tam giác IBC.
Lời giải:
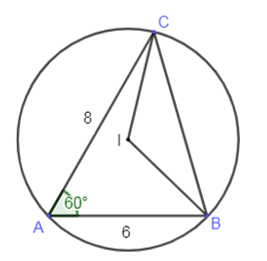
a)
b)
Áp dụng định lí côsin ta có:
Ta có: (áp dụng định lí sin)
Mặt khác, ta có: và cùng chắn cung BC
Mà là góc nội tiếp và góc ở tâm
Nên
Vậy
Bài 7 trang 73 Toán lớp 10 Tập 1: Cho tam giác ABC có trọng tâm G và độ dài ba cạnh AB, BC, CA lần lượt là 15, 18, 27.
a) Tính diện tích và bán kính đường tròn nội tiếp tam giác ABC.
b) Tính diện tích tam giác GBC.
Lời giải:
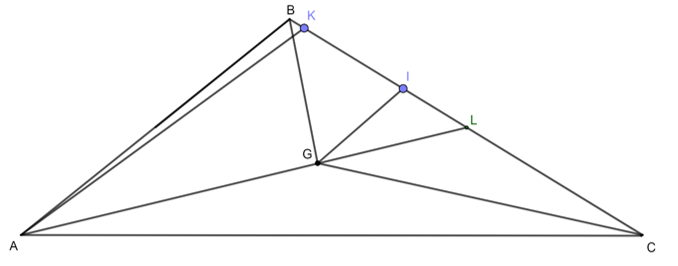
a) Ta có:
Áp dụng công thức Heron ta có:
b) Gọi K và I là lần lượt là hình chiếu của A và G lên BC
Áp dụng hệ quả của định lí Thales :
Bài 8 trang 73 Toán lớp 10 Tập 1: Cho ha là đường cao vẽ từ đỉnh A, R là bán kính đường tròn ngoại tiếp tam giác ABC. Chứng minh hệ thức ha = 2RsinBsinC.
Lời giải:
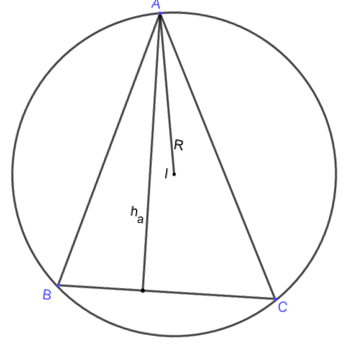
Ta có: (1)
Mà (2)
Từ (1) và (2) suy ra : (3)
Áp dụng định lí sin ta có: (4)
Thay (4) vào (3) ta được:
Bài 9 trang 73 Toán lớp 10 Tập 1: Cho tam giác ABC có góc B nhọn, AD và CE là hai đường cao.
b) Biết rằng SABC = 9SBDE và DE = . Tính cosB và bán kính đường tròn ngoại tiếp tam giác ABC.
Lời giải:
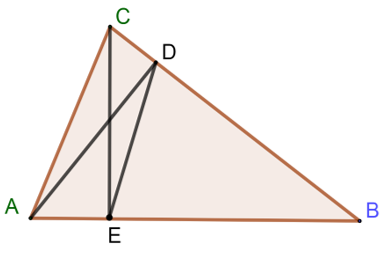
a) Ta có:
b) Theo đề ta có: (1)
Xét tam giác BCE vuông tại E ta có: (2)
Xét tam giác BDA vuông tại D ta có: (3)
Thay (2) và (3) vào (1) ta được : ( Vì góc B nhọn)
Mặt khác,
Áp dụng định lí sin cho tam giác BED ta có:
Xét tam giác BED và BCA ta có:
Góc B chung
và
Vậy tam giác AED đồng dạng với tam giác BCA nên
Theo đề ta có:
Bài 10 trang 73 Toán lớp 10 Tập 1: Cho tứ giác lồi ABCD có các đường chéo AC = x, BD = y và góc giữa AC và BD bằng α. Gọi S là diện tích của tứ giác ABCD.
b) Nêu kết quả trong trường hợp AC ⊥ BD.
Lời giải:
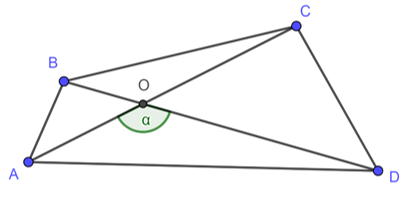
a) Ta có:
Ta có:
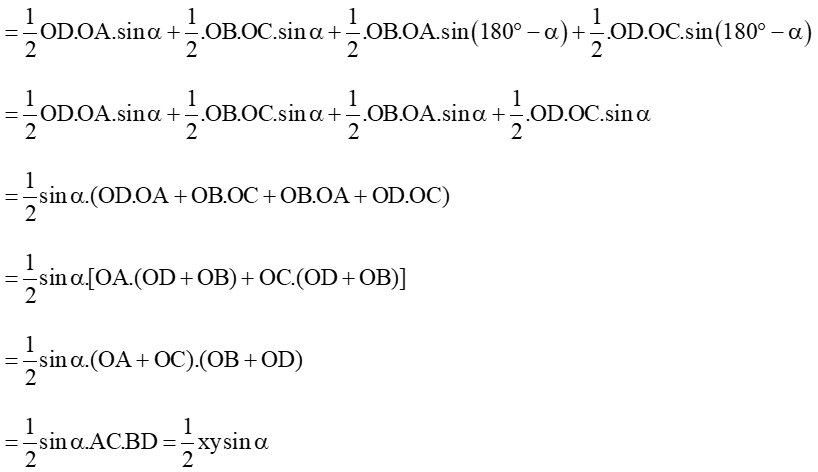
b) Trong trường hợp AC ⊥ BD thì nên .
Xem thêm lời giải bài tập Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:
Xem thêm lời giải bài tập Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:
Bài 3: Giải tam giác và ứng dụng thực tế
Xem thêm các chương trình khác:
- Soạn văn lớp 10 (hay nhất) – Chân trời sáng tạo
- Tác giả tác phẩm Ngữ văn lớp 10 – Chân trời sáng tạo
- Soạn văn lớp 10 (ngắn nhất) – Chân trời sáng tạo
- Tóm tắt tác phẩm Ngữ văn lớp 10 – Chân trời sáng tạo
- Giải sbt Ngữ văn lớp 10 – Chân trời sáng tạo
- Bố cục tác phẩm Ngữ văn lớp 10 – Chân trời sáng tạo
- Nội dung chính tác phẩm Ngữ văn lớp 10 – Chân trời sáng tạo
- Văn mẫu lớp 10 – Chân trời sáng tạo
- Giải Chuyên đề học tập Ngữ văn 10 – Chân trời sáng tạo
- Giải sgk Tiếng Anh 10 Friends Global – Chân trời sáng tạo
- Giải sbt Tiếng Anh 10 Friends Global – Chân trời sáng tạo
- Trọn bộ Từ vựng Tiếng Anh 10 Friends Global đầy đủ nhất
- Ngữ pháp Tiếng Anh 10 Friends Global
- Giải sgk Vật lí 10 – Chân trời sáng tạo
- Giải sbt Vật lí 10 – Chân trời sáng tạo
- Lý thuyết Vật lí 10 – Chân trời sáng tạo
- Giải Chuyên đề Vật lí 10 – Chân trời sáng tạo
- Giải sgk Hóa học 10 – Chân trời sáng tạo
- Lý thuyết Hóa học 10 – Chân trời sáng tạo
- Giải sbt Hóa học 10 – Chân trời sáng tạo
- Giải Chuyên đề Hóa học 10 – Chân trời sáng tạo
- Giải sgk Sinh học 10 – Chân trời sáng tạo
- Giải sbt Sinh học 10 – Chân trời sáng tạo
- Lý thuyết Sinh học 10 – Chân trời sáng tạo
- Giải Chuyên đề Sinh học 10 – Chân trời sáng tạo
- Giải sgk Lịch sử 10 – Chân trời sáng tạo
- Giải sbt Lịch sử 10 – Chân trời sáng tạo
- Giải Chuyên đề Lịch sử 10 – Chân trời sáng tạo
- Lý thuyết Lịch sử 10 – Chân trời sáng tạo
- Giải sgk Địa lí 10 – Chân trời sáng tạo
- Lý thuyết Địa Lí 10 - Chân trời sáng tạo
- Giải sbt Địa lí 10 – Chân trời sáng tạo
- Giải Chuyên đề Địa lí 10 – Chân trời sáng tạo
- Giải sgk Giáo dục Kinh tế và Pháp luật 10 – Chân trời sáng tạo
- Giải sbt Giáo dục Kinh tế và Pháp luật 10 – Chân trời sáng tạo
- Giải Chuyên đề Kinh tế và pháp luật 10 – Chân trời sáng tạo
- Lý thuyết KTPL 10 – Chân trời sáng tạo
- Giải sgk Hoạt động trải nghiệm 10 – Chân trời sáng tạo
- Giải sbt Hoạt động trải nghiệm 10 – Chân trời sáng tạo
- Giải sgk Giáo dục thể chất 10 – Chân trời sáng tạo
