Giải Toán 10 Bài 1 (Chân trời sáng tạo): Bất phương trình bậc nhất hai ẩn

Giải bài tập Toán 10 Bài 1: Bất phương trình bậc nhất hai ẩn

Video giải bài tập Toán 10 Bài 1: Bất phương trình bậc nhất hai ẩn

Giải Toán 10 trang 29 Tập 1

Hoạt động khởi động trang 29 Toán lớp 10 Tập 1: Đường thẳng d: y = x + 1 chia mặt phẳng tọa độ thành hai miền (không tính đường thẳng d) như hình bên. Dùng các nhãn dưới đây đặt vào miền phù hợp để đặt tên cho miền đó.

Lời giải:

Sau bài học này ta sẽ giải được bài toán như sau:

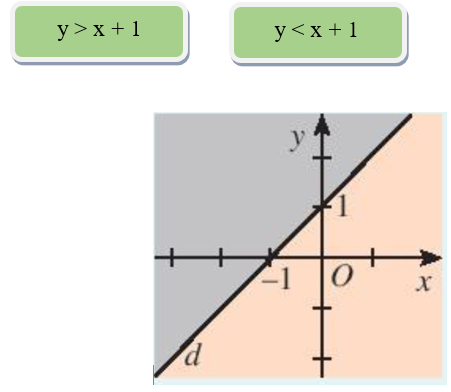
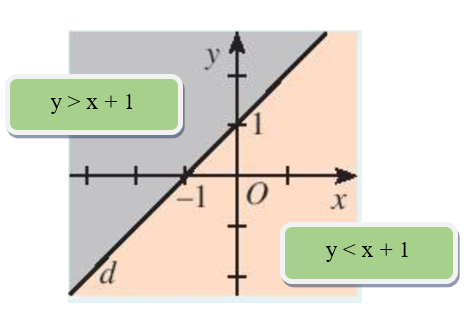
Ta chọn nhãn chứa bất phương trình y > x + 1 ở phía miền có màu xám và nhãn dán

y < x + 1 ở miền có màu hồng nhạt.

1. Khái niệm bất phương trình bậc nhất hai ẩn

Hoạt động khám phá 1 trang 29 Toán lớp 10 Tập 1: Bạn Nam để dành được 700 nghìn đồng. Trong một đợt ủng hộ các bạn học sinh ở vùng bị bão lụt, Nam đã ủng hộ x tờ tiền có mệnh giá 20 nghìn đồng, y tờ tiền có mệnh giá 50 nghìn đồng từ tiền để dành của mình.

a) Biểu diễn tổng số tiền bạn Nam đã ủng hộ theo x và y

b) Giải thích tại sao lại có bất đẳng thức 20x + 50y ≤ 700.

Lời giải:

a)

- Số tiền Nam đã ủng hộ theo mệnh giá 20 nghìn đồng là: 20.x (nghìn đồng);

- Số tiền Nam đã ủng hộ theo mệnh giá 50 nghìn đồng là: 50.y (nghìn đồng);

Như vậy tổng số tiền Nam đã ủng hộ là: 20x + 50y (nghìn đồng).

b)

Ta có: 20x + 50y chính là số tiền mà Nam đã đem đi ủng hộ; 700 nghìn đồng chính là số tiền mà Nam đã để dành được. Như vậy, ta có thể hiểu số tiền Nam đã ủng hộ ít hơn hoặc bằng số tiền Nam đã để dành được. Trong toán học để thể hiện được điều đó, ta có thể biểu diễn bằng bất đẳng thức 20x + 50y ≤ 700.

Thực hành 1 trang 29 Toán lớp 10 Tập 1: Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn?

a) 2x – 3y + 1 ≤ 0;

b) x – 3y + 1 ≥ 0;

c) y – 5 > 0;

d) x – y² + 1 > 0

Lời giải:

- Xét BPT 2x ‒ 3y + 1 ≤ 0: ta thấy bất phương trình có dạng ax + by + c ≤ 0 với a = 2, b = ‒3 và c = 1. Do đó bất phương trình a) là bất phương trình bậc nhất hai ẩn.

- Xét BPT x - 3y + 1 ≥ 0: ta thấy bất phương trình có dạng ax + by + c ≥ 0 với a = 1, b = ‒3 và c = 1. Do đó bất phương trình b) là bất phương trình bậc nhất hai ẩn.

- Xét BPT y - 5 > 0: ta thấy bất phương trình có dạng ax + by + c > 0 với a = 0, b = 1 và c = -5. Do đó bất phương trình c) là bất phương trình bậc nhất hai ẩn.

- Bất phương d) không phải là bất phương trình bậc nhất hai ẩn vì chứa y².

2. Nghiệm của bất phương trình bậc nhất hai ẩn

Giải Toán 10 trang 30 Tập 1

Hoạt động khám phá 2 trang 30 Toán lớp 10 Tập 1: Trường hợp nào sau đây thỏa mãn tình huống nêu trong hoạt động khám phá 1.

Trường hợp 1: Nam ủng hộ 2 tờ tiền có mệnh giá 20 nghìn và 3 tờ tiền có mệnh giá 50 nghìn đồng.

Trường hợp 2: Nam ủng hộ 15 tờ tiền có mệnh giá 20 nghìn đồng và 10 tờ tiền có mệnh giá 50 nghìn đồng.

Lời giải:

Ở Hoạt động khám phá 1 ta có bất phương trình 20x + 50y ≤ 700.

Trường hợp 1: Ta thấy x = 2 và y = 3 thay vào bất phương trình 20x + 50y ≤ 700

Ta có: 20.2 + 3.50 = 190 < 700 (Thoả mãn với tình huống tại Hoạt động khám phá 1).

Trường hợp 2: Ta thấy x = 15 và y = 10 thay vào bất phương trình 20x + 50y ≤ 700

Ta có: 15.20 + 10.50 = 800 > 700 (Không thoả mãn với tình huống tại Hoạt động khám phá 1).

Thực hành 2 trang 30 Toán lớp 10 Tập 1: Cặp số nào sau đây là nghiệm của bất phương trình 4x – 7y – 28 ≥ 0.

a) (9 ; 1)

b) (2 ; 6)

c) (0 ; – 4)

Lời giải:

a) Thay giá trị x = 9; y = 1 vào bất phương trình 4x – 7y – 28 ≥ 0 ta được: 4.9 - 7.1 - 28 = 1 > 0 nên (9; 1) là nghiệm của bất phương trình.

b) Thay giá trị x = 2; y = 6 vào bất phương trình 4x - 7y - 28 ≥ 0 ta được: 4.2 - 7.6 - 28 = -62 < 0 nên (2; 6) không phải là nghiệm của bất phương trình.

c) Thay giá trị x = 0; y = -4 vào bất phương trình 4x - 7y - 28 ≥ 0 ta được: 4.0 - 7.(-4) - 28 = 0 nên (0; -4) là nghiệm của bất phương trình.

Vận dụng 1 trang 30 Toán lớp 10 Tập 1: Cho biết mỗi 100 g thịt bò chứa khoảng 26,1 g protein, một quả trứng nặng 44 g chứa khoảng 5,7 g protein (nguồn: https: www.vinmec.com). Giả sử có một người mỗi ngày cần không quá 60 g protein. Gọi số gam thịt bò và số quả trứng mà người đó ăn trong một ngày lần lượt là x và y.

a) Lập bất phương trình theo x, y diễn tả giới hạn về lượng protein trong khẩu phần ăn hằng ngày của người đó.

b) Dùng bất phương trình ở câu a) để trả lời hai câu hỏi sau:

- Nếu người đó ăn 150 g thịt bò và 2 quả trứng (mỗi quả 44 g) trong một ngày thì có phù hợp không?

- Nếu người đó ăn 200 g thịt bò và 2 quả trứng (mỗi quả 44 g) trong một ngày thì có phù hợp không?

Lời giải:

a)

+) 100 g thịt bò chứa khoảng 26,1 g protein, vậy 1 g thịt bò sẽ chứa khoảng $\frac{26,1}{100}$ g protein; Do đó x gam thịt bò sẽ chứa $\frac{26,1}{100}.x$ gam protein.

+) 44g trứng chứa 5,7g protein, vậy 1g trứng sẽ chứa $\frac{5,7}{44}$g protein

+) 1 quả trứng nặng 44g, vậy y quả trứng sẽ nặng y.44g,

Vì một người mỗi ngày cần không quá 60 g protein nên ta sẽ có bất phương trình sau: $\frac{26,1}{100}$.x + $\frac{5,7}{44}$.44.y ≤ 60

$\iff$$\frac{26,1}{100}$.x + 5,7.y - 60 ≤ 0

$\iff$0,261x + 5,7y - 60 ≤ 0.

Vậy bất phương trình cần tìm là 0,261x + 5,7y – 60 ≤ 0.

b)

+) Với x = 150; y = 2 ta thay vào bất phương trình 0,261x + 5,7y – 60 ≤ 0.

150.0,261 + 5,7.2 - 60 = -9,45 ≤ 0 là mệnh đề đúng.

Vậy người đó ăn 150 g thịt bò và 2 quả trứng (mỗi quả 44 g) trong một ngày là phù hợp.

+) Với x = 200; y = 2 ta thay vào bất phương trình 0,261x + 5,7y – 60 ≤ 0.

200.0,261 + 5,7.2 - 60 = 3,6 ≤ 0 là mệnh đề sai.

Vậy người đó ăn 200 g thịt bò và 2 quả trứng (mỗi quả 44 g) trong một ngày là không phù hợp.

3. Biểu diễn miền nghiệm của bất phương trình bậc nhất hai ẩn

Hoạt động khám phá 3 trang 30 Toán lớp 10 Tập 1: Cho bất phương trình 2x – y + 1 < 0

a) Vẽ đường thẳng y = 2x + 1

b) Các cặp số (–2;0), (0; 0), (1; 1) có là nghiệm của bất phương trình đã cho không.

Lời giải:

a) Tập xác định: D = $ℝ$

- Cho x = 0 thay vào y = 2x + 1 ta được y = 1 $\Rightarrow$ Ta lấy được điểm (0; 1).

- Cho y = 0 thay vào y = 2x + 1 ta được x = $\frac{-1}{2}$ $\Rightarrow$Ta lấy được điểm ($\frac{-1}{2}$; 0).

Như vậy đồ thị của y = 2x + 1 là đường thẳng đi qua hai điểm trên.

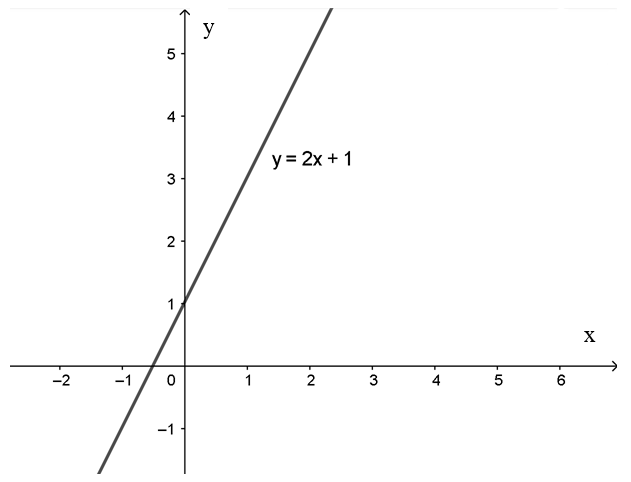
b)

- Thay x = -2; y = 0 vào bất phương trình 2x - y +1 < 0 ta được: 2.(-2) - 0 + 1 = -3 < 0 là mệnh đề đúng. Do đó điểm (-2; 0) là nghiệm của bất phương trình.

- Thay x = 0; y = 0 vào bất phương trình 2x - y + 1 < 0 ta được: 2.0 - 0 + 1 = 1 < 0 là mệnh đề sai. Do đó điểm (0; 0) không phải là nghiệm của bất phương trình.

- Thay x = 1; y = 1 vào bất phương trình 2x - y + 1 < 0 ta được: 2.1 - 1 + 1 = 2 < 0 là

Giải Toán 10 trang 32 Tập 1

Thực hành 3 trang 32 Toán lớp 10 Tập 1: Biểu diễn miền nghiệm của các bất phương trình sau :

a) 2x + y – 2 ≤ 0

b) x – y – 2 ≥ 0

Lời giải:

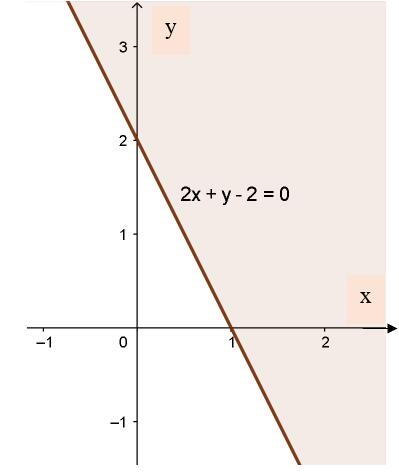
a) Vẽ đường thẳng d: 2x + y - 2 = 0 đi qua hai điểm A (0; 2) và B (1; 0).

Xét gốc toạ độ O (0; 0), ta thấy: O d và 2.0 + 0 - 2 = -2 < 0.

Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng (kể cả bờ d) chứa gốc toạ độ O (Miền không tô màu trong hình vẽ).

b) Vẽ đường thẳng d: x - y - 2 = 0 đi qua hai điểm (0; -2); (2; 0).

Xét gốc toạ độ O (0; 0) ta thấy: O ∉ d và 0 - 0 - 2 = -2 < 0.

Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng không chứa điểm O (Kể cả bờ d) (Miền không tô màu).

Vận dụng 2 trang 32 Toán lớp 10 Tập 1: Biểu diễn miền nghiệm của hai bất phương trình sau trên cùng một mặt phẳng tọa độ Oxy.

a) y ≥ 2

b) x ≤ 4.

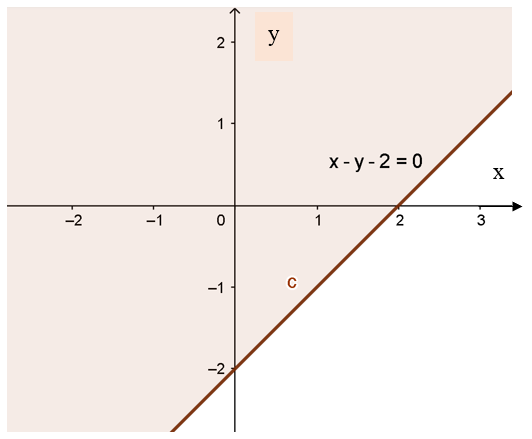
Lời giải:

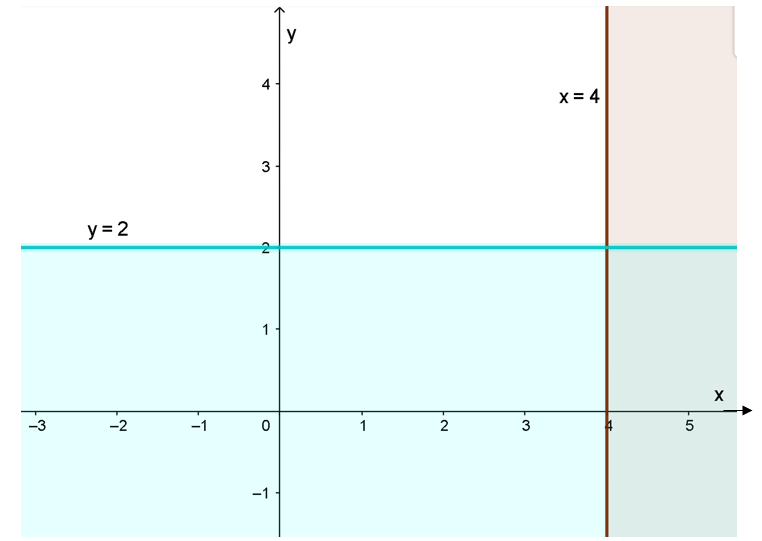
a) Vẽ đường thẳng d: y - 2 = 0 song song với trục Ox và qua điểm (0; 2).

Xét gốc toạ độ O (0; 0) ta thấy: O ∉ d và 0 - 2 = -2 < 0.

Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng không chứa điểm O (Kể cả bờ d) (Miền không tô màu xanh)

b) Vẽ đường thẳng c: x - 4 = 0 song song với trục Oy và qua điểm (4; 0).

Xét gốc toạ độ O (0; 0) ta thấy: O ∉ c và 0 - 4 = -4 < 0.

Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng chứa điểm O (Kể cả bờ d) (Miền không tô màu hồng).

Khi đó ta có hình vẽ:

Bài tập

Bài 1 trang 32 Toán lớp 10 Tập 1: Cho bất phương trình bậc nhất hai ẩn x - 2y + 6 > 0.

a) (0 ; 0) có phải là một nghiệm của bất phương trình đã cho không?

b) Chỉ ra ba cặp số (x ; y) là nghiệm của bất phương trình đã cho.

c) Biểu diễn miền nghiệm của bất phương trình đã cho trên mặt phẳng tọa độ Oxy.

Lời giải:

Bài 2 trang 32 Toán lớp 10 Tập 1: Biểu diễn tập nghiệm của các bất phương trình sau trên mặt phẳng tọa độ Oxy.

a) – x + y + 2 > 0

b) y + 2 ≥ 0

c ) – x + 2 ≤ 0.

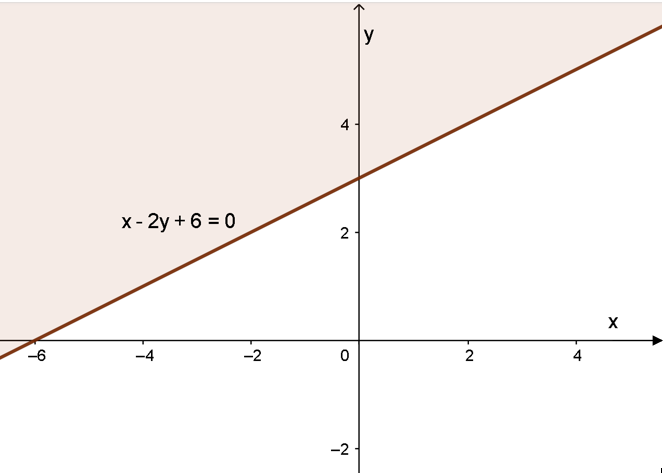
Lời giải:

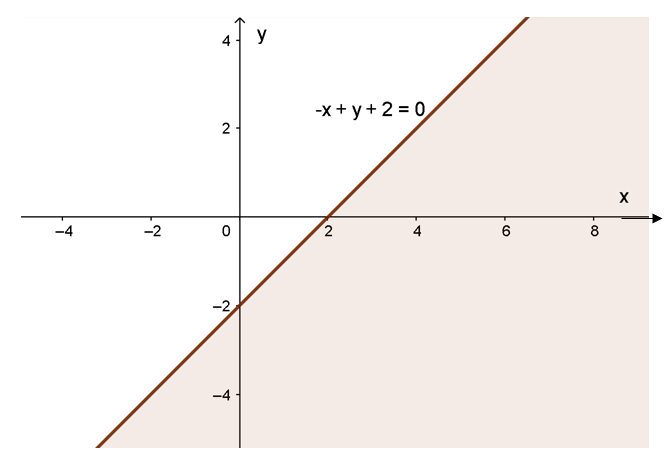
a) Vẽ đường thẳng d: -x + y + 2 = 0 qua hai điểm (0; -2); (2; 0).

Xét gốc toạ độ O(0; 0) ta thấy: O ∉ d và -0 + 0 + 2 = 2 > 0. Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng chứa điểm O (không kể bờ d) (miền không tô màu).

b)

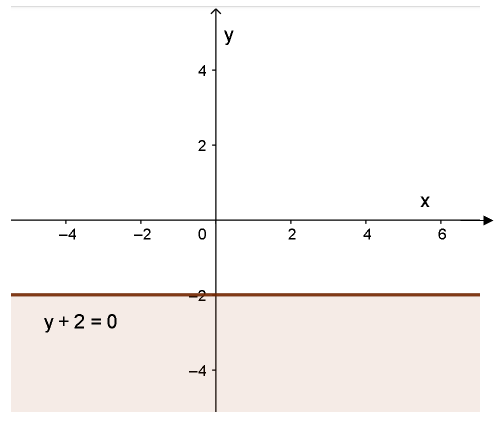
Vẽ đường thẳng d: y + 2 = 0 song song với Ox và qua điểm (0; -2)

Xét gốc toạ độ O (0; 0) ta thấy: O ∉ d và 0 + 2 = 2 > 0. Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng chứa điểm O (kể cả bờ d) (miền không tô màu).

c)

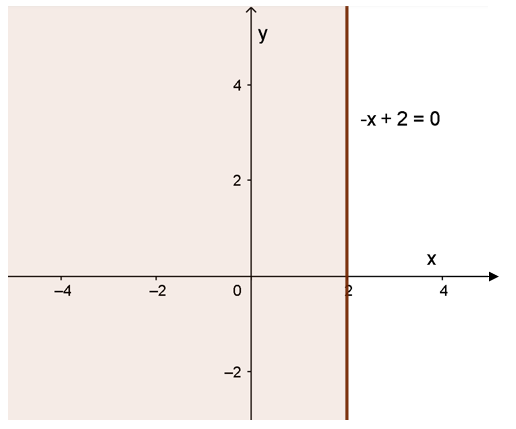
Vẽ đường thẳng d: -x + 2 = 0 song song với Oy và qua điểm (2; 0).

Xét gốc toạ độ O (0; 0) ta thấy: O ∉ d và ‒0 + 2 = 2 > 0. Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng không chứa điểm O (kể cả bờ d) (miền không màu).

Bài 3 trang 32 Toán lớp 10 Tập 1: Biểu diễn miền nghiệm của các bất phương trình sau trên mặt phẳng tọa độ oxy

a) – x + 2 + 2(y – 2) < 2(1 – x)

b) 3(x – 1 ) + 4(y – 2) < 5x – 3.

Lời giải:

a) -x + 2 + 2(y - 2) < 2(1 - x)

$\iff$ -x + 2 + 2y - 4 < 2 - 2x

$\iff$-x + 2 + 2y - 4 - 2 + 2x < 0

$\iff$x + 2y - 4 < 0

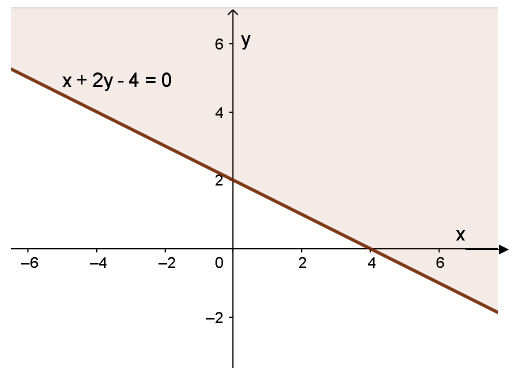
Vẽ đường thẳng d: x + 2y - 4 = 0 đi qua hai điểm (0; 2); (4; 0).

Xét gốc toạ độ O (0; 0) ta thấy: O ∈ d và 0 + 2.0 - 4 = - 4 < 0. Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng chứa điểm O (không kể bờ d) (miền không màu).

b)

3(x - 1) + 4(y - 2) < 5x – 3

$\iff$3x - 3 + 4y - 8 < 5x - 3

$\iff$3x - 3 + 4y - 8 - 5x + 3 < 0

$\iff$-2x + 4y - 8 < 0

$\iff$x – 2y + 4 > 0

Vẽ đường thẳng d: x – 2y + 4 = 0 đi qua hai điểm (0; 2); (-4; 0).

Xét gốc toạ độ O (0; 0) ta thấy: O ∈ d và 0 - 2.0 + 4 = 4 > 0. Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng chứa điểm O (không kể bờ d) (miền không màu).

Bài 4 trang 32 Toán lớp 10 Tập 1: Bạn Cúc muốn pha hai loại nước cam. Để pha một lít nước cam loại I cần 30 g bột cam, còn một lít nước cam loại II cần 20 g bột cam. Gọi x và y lần lượt là số lít nước cam loại I và II pha chế được. Biết rằng Cúc chỉ có thể dùng không quá 100 g bột cam. Hãy lập các bất phương trình mô tả số lít nước cam loại I và II mà bạn Cúc có thể pha chế được và biểu diễn miền nghiệm của các bất phương trình đó trên cùng một mặt phẳng tọa độ Oxy.

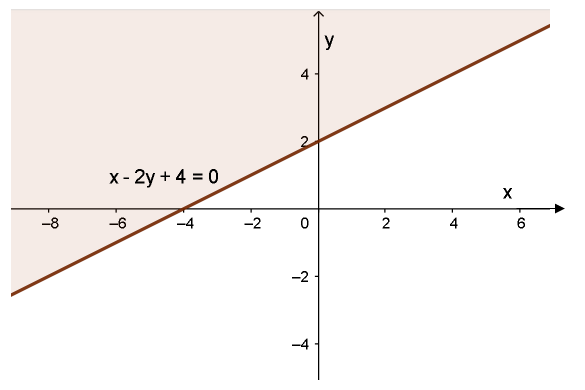
Lời giải:

- Số lit nước cam: x ≥ 0, y ≥ 0.

Để pha được x lít nước cam loại I thì Cúc cần số gam bột cam là: 30x (g).

Để pha được y lít nước cam loại II thì Cúc cần số gam bột cam là: 20y (g).

- Nếu Cúc chỉ pha nước cam loại I, ta có bất phương trình: 30x ≤ 100;

- Nếu Cúc chỉ pha nước cam loại II, ta có bất phương trình: 20y ≤ 100;

- Nếu Cúc pha cả nước cam loại I và loại II, ta có bất phương trình:

30x + 20y ≤ 100 ⇔ 30x + 20y – 100 ≤ 0.

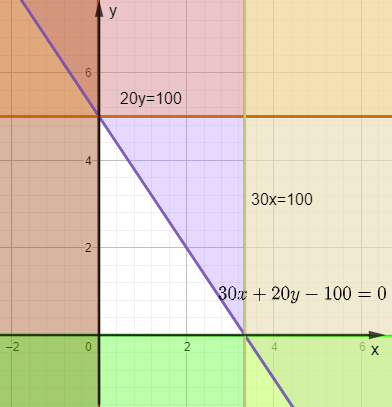
Biểu diễn miền nghiệm của các bất phương trình trên:

- Miền nghiệm của bất phương trình 30x ≤ 100 là phần mặt phẳng chứa điểm O (kể cả đường thẳng 30x - 100 = 0) được xác định bởi đường thẳng 30x - 100 = 0.

- Miền nghiệm của bất phương trình 20y ≤ 100 là phần mặt phẳng chứa điểm O (kể cả đường thẳng 20y - 100 = 0) được xác định bởi đường thẳng 20y - 100 = 0.

- Miền nghiệm của bất phương trình 30x + 20y - 100 ≤ 0 là phần mặt phẳng chứa điểm O (kể cả đường thẳng 30x + 20y - 100 = 0) được xác định bởi đường thẳng 30x + 20y - 100 = 0.

Phần không màu là miền nghiệm của các bất phương trình như trên hình vẽ dưới đây:

Bài 5 trang 32 Toán lớp 10 Tập 1: Miền không gạch chéo (không kể bờ d) trong mỗi hình dưới đây là miền nghiệm của bất phương trình nào ?

Lời giải:

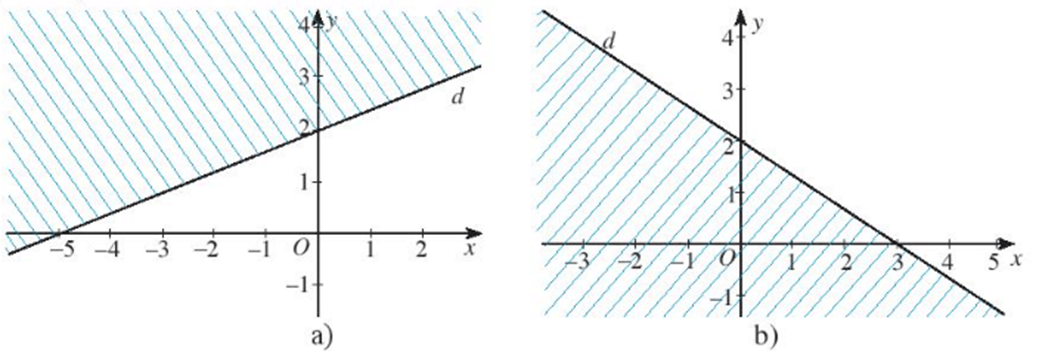
a) Nhận thấy đường thẳng d đi qua hai điểm (0; 2); (-5; 0) và có dạng y = ax + b (a, b ≠ 0).

Khi đó ta thay lần lượt giá trị của hoành độ và tung độ của các điểm vào phương trình y = ax + b ta được: $\left\{\begin{array}{l}2=b\\ 0=-5\text{a}+b\end{array}\right.$$\iff$$\left\{\begin{array}{l}b=2\\ a=\frac{2}{5}\end{array}\right.$.

Như vậy ta có phương trình d: y = $\frac{2}{5}$x + 2 hay y - $\frac{2}{5}$x - 2 = 0.

Xét điểm O (0; 0), thay giá trị x = 0; y = 0 vào phương trình d: y - $\frac{2}{5}$x - 2 = 0 ta được

0 - $\frac{2}{5}$.0 - 2 = -2 < 0 mà miền nghiệm là miền chứa điểm O và không kể bờ d nên ta suy ra bất phương trình biểu diễn miền nghiệm là: y - $\frac{2}{5}$x - 2 < 0.

b)

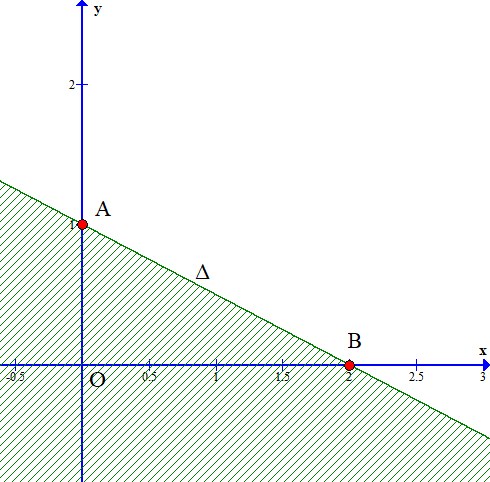
Nhận thấy đường thẳng d đi qua hai điểm (0; 2); (3; 0) và có dạng y = ax + b (a, b ≠ 0).

Khi đó ta thay lần lượt giá trị của hoành độ và tung độ của các điểm vào phương trình y = ax + b ta được: $\left\{\begin{array}{l}2=b\\ 0=3\text{a}+b\end{array}\right.$$\iff$$\left\{\begin{array}{l}b=2\\ a=-\frac{2}{3}\end{array}\right.$.

Như vậy ta có phương trình d: y = $-\frac{2}{3}x$ + 2 hay y + $\frac{2}{3}$x - 2 = 0

Xét điểm O (0; 0), thay giá trị x = 0; y = 0 vào phương trình d: y + $\frac{2}{3}$x - 2 = 0 ta được

0 + $\frac{2}{3}$.0 - 2 = -2 < 0 mà miền nghiệm là miền không chứa điểm O và không kể bờ d nên ta suy ra bất phương trình biểu diễn miền nghiệm là: y + $\frac{2}{3}$x - 2 > 0.

Lý thuyết Toán 10 Bài 1: Bất phương trình bậc nhất hai ẩn - Chân trời sáng tạo

1. Khái niệm bất phương trình bậc nhất hai ẩn

- Bất phương trình bậc nhất hai ẩn x, y là bất phương trình có một trong các dạng

ax + by + c < 0; ax + by + c > 0; ax + by + c ≤ 0; ax + by + c ≥ 0,

trong đó a, b, c là những số cho trước, a, b không đồng thời bằng 0, x và y là các ẩn.

Ví dụ:

5x + 2y < 4 là bất phương trình bậc nhất hai ẩn vì bất phương trình chứa hai ẩn x, y ở bậc nhất.

5x + 2y – 3z > 3 không là bất phương trình bậc nhất hai ẩn vì bất phương trình này chứa 3 ẩn x, y, z ở bậc nhất.

2. Nghiệm của bất phương trình bậc nhất hai ẩn

Xét bất phương trình ax + by + c < 0.

Mỗi cặp số (x₀; y₀) thỏa mãn ax₀ + by₀ + c < 0 được gọi là một nghiệm của bất phương trình đã cho.

Chú ý: Nghiệm của các bất phương trình ax + by + c > 0; ax + by + c ≤ 0; ax + by + c ≥ 0 được định nghĩa tương tự.

Ví dụ:

+ Bất phương trình bậc nhất hai ẩn 5x + 2y < 4 có các cặp nghiệm là (-1; -2); (0; 0); bởi:

Với x = ‒1, y = ‒2 ta có: 5.(‒1) + 2.(‒2) = ‒9 < 4 nên (‒1; ‒2) là nghiệm của bất phương trình 5x + 2y < 4.

Với x = 0, y = 0 ta có: 5. 0 + 2. 0 = 0 < 4 nên (0; 0) là nghiệm của bất phương trình 5x + 2y < 4.

+ Bất phương trình bậc nhất hai ẩn x ‒ 2y ≥ 4 có các cặp nghiệm là (4; ‒1); (4; 0); bởi:

Với x = 4, y = ‒1 ta có: 4 – 2. (‒1) = 6 ≥ 4 nên (4; ‒1) là nghiệm của bất phương trình x ‒ 2y ≥ 4.

Với x = 4, y = 0 ta có: 4 ‒ 2. 0 = 4 ≥ 4 nên (4; 0) là nghiệm của bất phương trình x ‒ 2y ≥ 4.

3. Biểu diễn miền nghiệm của bất phương trình bậc nhất hai ẩn

- Trong mặt phẳng tọa độ Oxy, tập hợp các điểm (x₀; y₀) sao cho ax₀ + by₀ + c < 0 được gọi là miền nghiệm của bất phương trình ax + by + c < 0.

- Người ta chứng minh được: Mỗi phương trình ax + by + c = 0 (a, b không đồng thời bằng 0) xác định một đường thẳng ∆. Đường thẳng ∆ chia mặt phẳng tọa độ Oxy thành hai nửa mặt phẳng, trong đó một nửa (không kể bờ ∆) là tập hợp các điểm (x; y) thỏa mãn ax + by + c > 0, nửa còn lại (không kể bờ ∆) là tập hợp các điểm (x; y) thỏa mãn ax + by + c < 0.

Ta có thể biểu diễn miền nghiệm của bất phương trình bậc nhất hai ẩn ax + by + c < 0 như sau:

Bước 1: Trên mặt phẳng tọa độ Oxy, vẽ đường thẳng ∆: ax + by +c = 0.

Bước 2: Lấy một điểm (x₀; y₀) không thuộc ∆. Tính ax₀ +by₀ + c.

+ Nếu ax₀ + by₀ + c < 0 thì miền nghiệm của bất phương trình đã cho là nửa mặt phẳng (không kể bờ ∆) chứa điểm (x₀; y₀).

+ Nếu ax₀ + by₀ + c > 0 thì miền nghiệm của bất phương trình đã cho là nửa mặt phẳng (không kể bờ ∆) không chứa điểm (x₀; y₀).

Chú ý: Đối với các bất phương trình bậc nhất hai ẩn dạng ax + by + c ≤ 0 (hoặc ax + by + c ≥ 0) thì miền nghiệm là miền nghiệm của bất phương trình ax + by + c < 0 (hoặc ax + by + c > 0) kể cả bờ.

Ví dụ: Biểu diễn miền nghiệm của bất phương trình x + 2y – 2 > 0 trên mặt phẳng tọa độ:

Bước 1: Vẽ đường thẳng ∆: x + 2y – 2 = 0 trên mặt phẳng tọa độ Oxy.

Bước 2: Lấy điểm O (0; 0) không thuộc ∆ và thay x = 0 và y = 0 vào biểu thức x + 2y – 2 ta được 0 + 2.0 – 2 = ‒2 > 0 là mệnh đề sai.

Do đó miền nghiệm của bất phương trình là nửa mặt phẳng bờ ∆ (không kể bờ ∆) không chứa điểm O (miền nghiệm là miền không bị gạch trên hình)

Xem thêm lời giải bài tập Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:

Bài 2: Hệ bất phương trình bậc nhất hai ẩn

Bài tập cuối chương 2

Bài 1: Hàm số và đồ thị

Bài 2: Hàm số bậc hai

Bài tập cuối chương 3

Xem thêm tài liệu Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:

Lý thuyết Bài 1: Bất phương trình bậc nhất hai ẩn