Giải Toán 10 Bài 3 (Chân trời sáng tạo): Tích của một số với một vectơ
Với giải bài tập Toán lớp 10 Bài 3: Tích của một số với một vectơ sách Chân trời sáng tạo hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 10 Bài 3.
Giải bài tập Toán 10 Bài 3: Tích của một số với một vectơ
1. Tích của một số với một vectơ và các tính chất
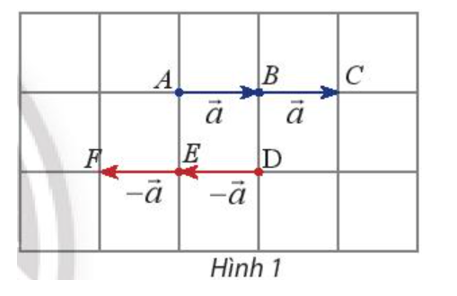
Lời giải:
Vectơ →a+→a có hướng từ A sang C.
Vectơ (−→a)+(−→a) có hướng từ D sang F.
Thực hành 1 trang 95 Toán lớp 10 Tập 1: Cho hai vectơ →a,→b và một điểm M như Hình 3.
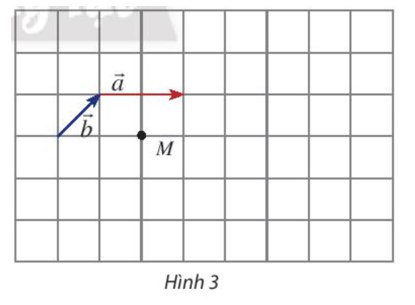
a) Hãy vẽ các vectơ →MN=3→a, →MP=−3→b .
b) Cho biết mỗi ô vuông có cạnh bằng 1. Tính: |3→b|, |−3→b|, |2→a+2→b|.
Lời giải:
a) Ta thấy 3 > 0 nên hai vectơ →MN và →a cùng hướng.
Do đó từ M kẻ đường thẳng d song song với đường thẳng a.
Trên đường thẳng d, về bên phải điểm M chọn điểm N sao cho MN = 6.
Khi đó →MN=3→a.
Do -3 < 0 nên hai vectơ →MP và →b ngược hướng.
Do đó từ M kẻ đường thẳng c song song với đường thẳng b.
Trên đường thẳng c, về bên trái điểm M chọn P sao cho MP = 3.
Khi đó →MP=−3→b.
Ta có hình vẽ như sau:
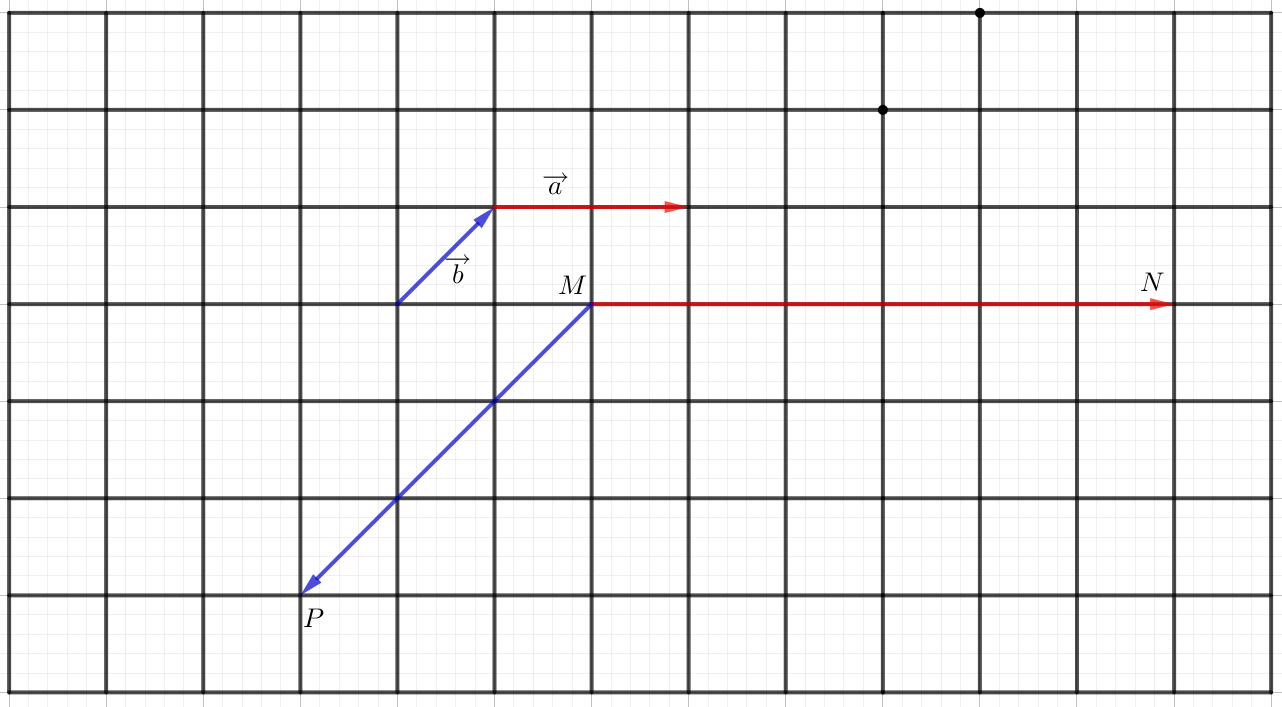
b) Ta thấy MP là độ dài cạnh huyền của 1 tam giác vuông cân có cạnh bằng 3.
Do đó MP = √32+32=3√2.
Ta thấy 3→b và −3→b là hai vectơ đối nên |3→b|=|−3→b|=|→MP|=3√2.
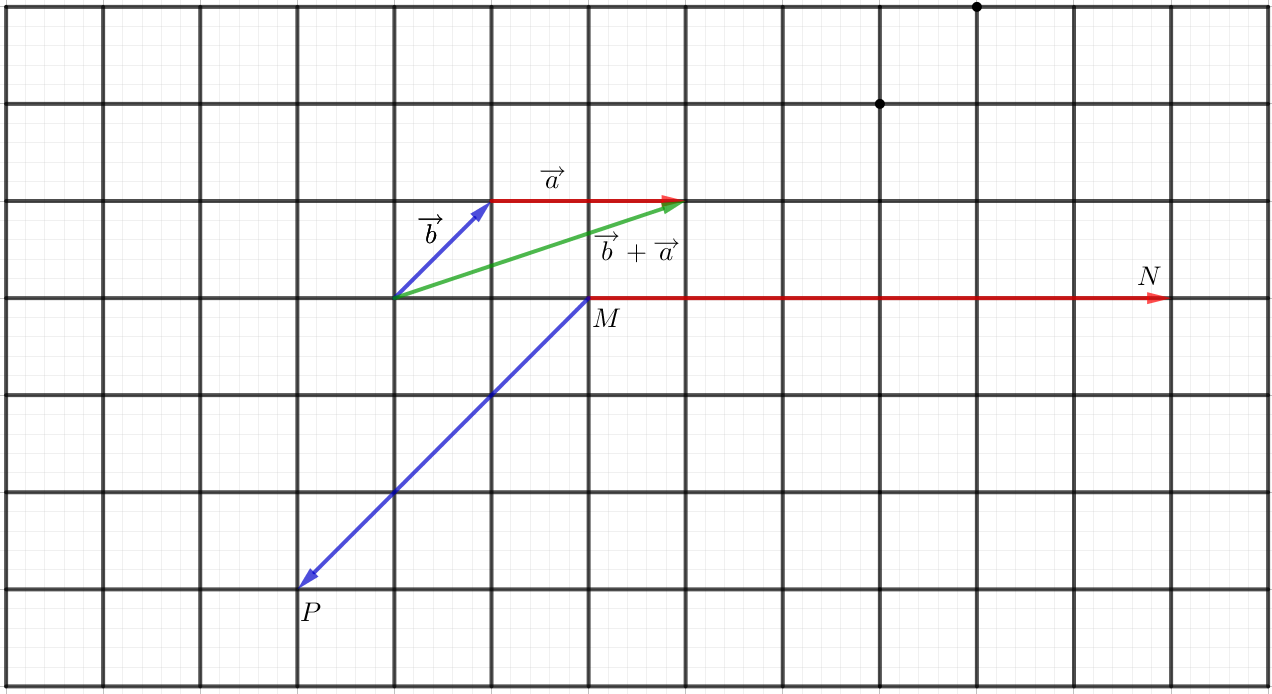
Ta thấy |→b+→a| là độ cạnh huyền của 1 tam giác vuông có độ dài 2 cạnh góc vuông lần lượt là 1 và 3.
Khi đó |→b+→a|=√32+12=√10.
Do đó |2→b+2→a|=|2→a+2→b|=2√10.
Vậy |3→b|=|−3→b|=3√2; |2→a+2→b|=2√10.
Lời giải:
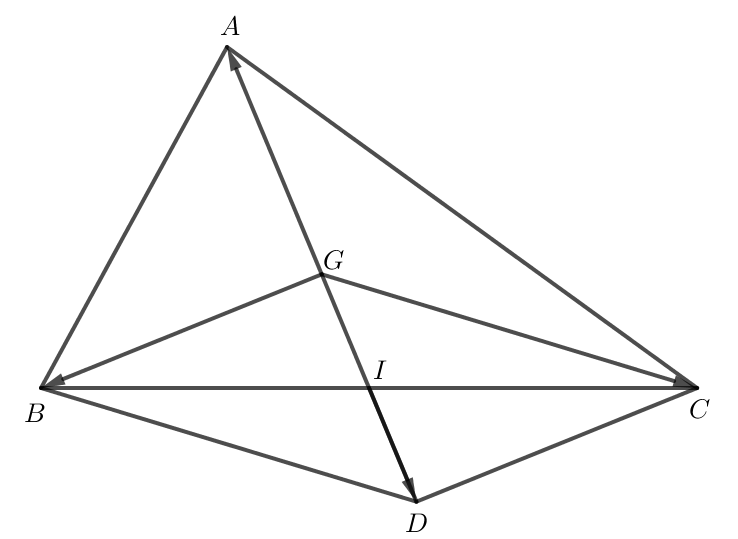
Phần thuận: G là trọng tâm của tam giác ABC thì →MA+→MB+→MC=3→MG.
Chứng minh:
Do G là trọng tâm của tam giác ABC nên →GA+→GB+→GC=→0.
Do đó →MG+→GA+→MG+→GB+→MG+→GC=3→MG hay →MA+→MB+→MC=3→MG.
Phần đảo: Tam giác ABC có →MA+→MB+→MC=3→MG thì G là trọng tâm của tam giác ABC.
Chứng minh:
→MA+→MB+→MC=3→MG
⇒→MG+→GA+→MG+→GB+→MG+→GC=3→MG
⇒→GA+→GB+→GC=→0
Dựng hình bình hành GBDC và gọi I là giao điểm của GD và BC.
Áp dụng quy tắc hình bình hành ta có →GB+→GC=→GD.
Mà →GA+→GB+→GC=→0 hay →GA+→GD=→0.
Do đó →GA=−→GD.
Khi đó |→GA|=|−→GD| hay GA = GD.
Hình bình hành GBDC có I là giao điểm hai đường chéo GD và BC nên I là trung điểm của BC và I là trung điểm của GD.
Do I là trung điểm của GD nên GI = 12GD = 12GA.
GI = 12GA nên AI = GI + GA = 12GA + GA = 32GA hay AG = 23AI.
Tam giác ABC có AI là đường trung tuyến, lại có AG = 23AI nên G là trọng tâm của tam giác ABC.
Vậy ta có điều phải chứng minh.
Vận dụng trang 95 Toán lớp 10 Tập 1: Một con tàu chở hàng A đang đi về hướng tây với tốc độ 20 hải lí/giờ. Cùng lúc đó, một con tàu chở khách B đang đi về hướng đông với tốc độ 50 hải lí/giờ. Biểu diễn vectơ vận tốc →b của tàu B theo vectơ vận tốc →a của tàu A.
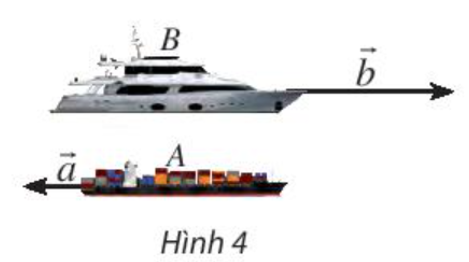
Lời giải:
Ta thấy hai vectơ →a và →b ngược hướng và |→b|=50; |→a|=20.
⇒|→b|=52|→a|.
Vậy →b=−52→a.
2. Điều kiện để hai vectơ cùng phương
Lời giải:
Ta thấy với →b khác →0 thì |→a||→b| ≥ 0.
Do đó hai vectơ →c và →b là hai vectơ cùng hướng.
Mà →a và →b là hai vectơ cùng phương nên hai vectơ →a và →c cùng hướng khi hai vectơ →a và →b cùng hướng; hai vectơ →a và →c ngược hướng khi hai vectơ →a và →b ngược hướng.
Do →c=|→a||→b|.→b nên |→c|=||→a||→b|.→b|=|→a||→b|.|→b|=|→a|.
Do đó độ dài của hai vectơ →a và →c bằng nhau.
Lời giải:
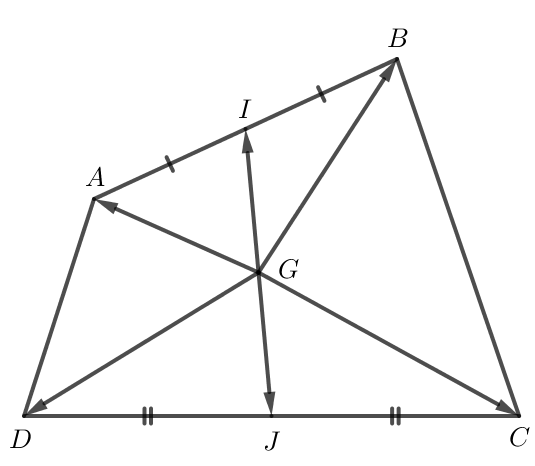
Do I là trung điểm của AB nên →GA+→GB=2→GI.
Do J là trung điểm của CD nên →GC+→GD=2→GJ.
Do đó →GA+→GB+→GC+→GD=2→GI+2→GJ hay →GI+→GJ=→0.
Do →GI+→GJ=→0 nên G là trung điểm của IJ.
Vậy I, G, J thẳng hàng.
Bài tập
Lời giải:
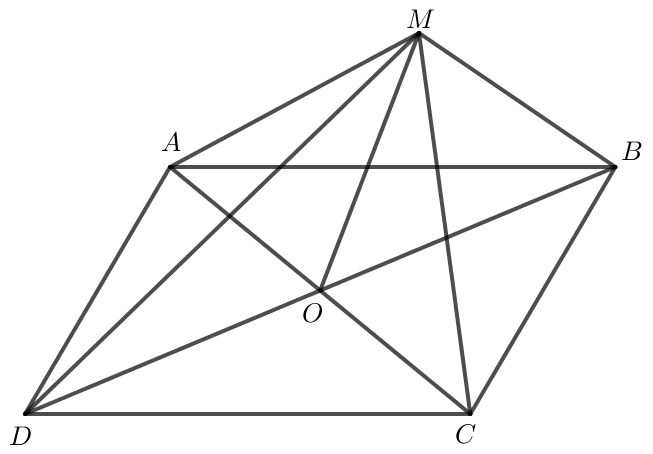
a) Hình bình hành ABCD có O là giao điểm hai đường chéo nên OA = OC, OB = OD.
Khi đó →OA và →OC là hai vectơ đối, →OB và →OD là hai vectơ đối.
Do đó →OA+→OB+→OC+→OD=→0.
Ta có
→MA+→MB+→MC+→MD=→MO+→OA+→MO+→OB+→MO+→OC+→MO+→OD
=4→MO+(→OA+→OB+→OC+→OD)
=4→MO
Vậy →MA+→MB+→MC+→MD=4→MO.
b) Áp dụng quy tắc hình bình hành ta có →AB+→AD=→AC.
Do đó →AB+→AD+→AC=→AC+→AC hay →AB+→AC+→AD=2→AC.
Vậy →AB+→AC+→AD=2→AC.
Lời giải:
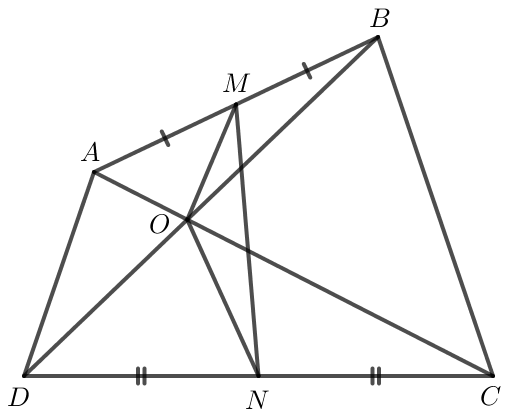
a) Gọi O là giao điểm hai đường chéo của tứ giác ABCD.
Do M là trung điểm của AB nên →OA+→OB=2→OM.
Do đó →AO+→BO=2→MO.
Do N là trung điểm của CD nên →OC+→OD=2→ON.
Do đó →AO+→BO+→OC+→OD=2→MO+2→ON.
hay →AO+→OC+→BO+→OD=2→MN.
Do đó →AC+→BD=2→MN.
b) Ta có →AD=→AC+→CD
Do đó
→BC+→AD=→BC+→AC+→CD=→AC+(→BC+→CD)=→AC+→BD.
Vậy →AC+→BD=→BC+→AD.
Lời giải:
Do →MA+4→MB=→0 nên →MA=−4→MB do đó |→MA|=|−4||→MB|=4|→MB| hay MA = 4MB.
Ta thấy -4 < 0 nên hai vectơ →MA và →MB ngược hướng.
Do đó A và B nằm ở hai phía so với điểm M.
Ta thực hiện vẽ như sau:
Bước 1. Vẽ đường thẳng d, trên đường thẳng d xác định hai điểm M và B.
Bước 2. Trên đường thẳng d, xác định điểm A sao cho A và B nằm ở hai phía so với điểm M thỏa mãn MA = 4MB.
Ta có hình vẽ như sau:

Lời giải:
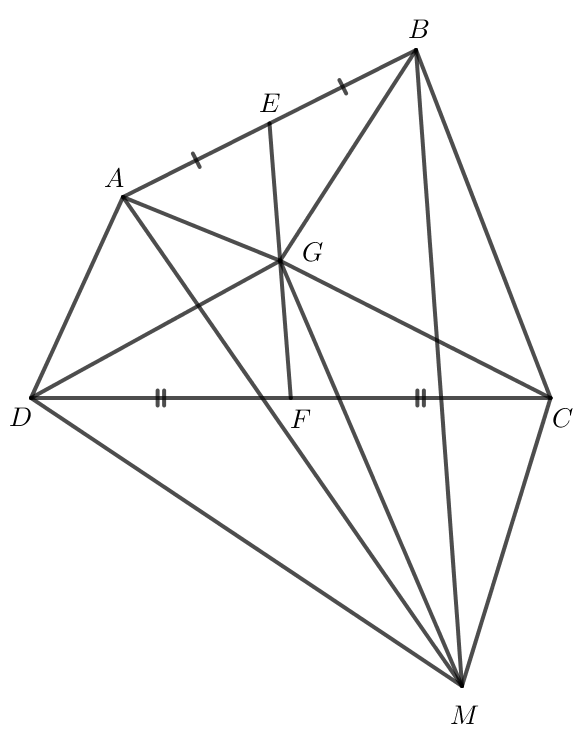
Do E là trung điểm của AB nên →GA+→GB=2→GE.
Do F là trung điểm của CD nên →GC+→GD=2→GF.
Do G là trung điểm của EF nên →GE+→GF=→0.
Do đó →GA+→GB+→GC+→GD=2→GE+2→GF=2(→GE+→GF)=→0.
Ta có
→MA+→MB+→MC+→MD=→MG+→GA+→MG+→GB+→MG+→GC+→MG+→GD
=4→MG+(→GA+→GB+→GC+→GD)
=4→MG
Vậy →MA+→MB+→MC+→MD=4→MG.
Bài 5 trang 97 Toán lớp 10 Tập 1: Máy bay A đang bay về hướng đông bắc với tốc độ 600 km/h. Cùng lúc đó, máy bay B đang bay về hướng tây nam với tốc độ 800 km/h. Biểu diễn vectơ vận tốc →b của máy bay B theo vectơ vận tốc →a của máy bay A.
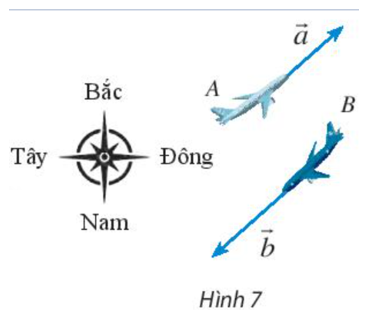
Lời giải:
Ta thấy hai vectơ →a và →b ngược hướng và |→a| = 600, |→b| = 800.
Do đó |→b|=800600|→a|=43|→a| hay b = 43a.
Mà hai vectơ →a và →b ngược hướng nên →b=−43→a.
Vậy →b=−43→a.
Bài 6 trang 97 Toán lớp 10 Tập 1: Cho hai điểm phân biệt A và B.
a) Xác định điểm O sao cho →OA+3→OB=→0.
b) Chứng minh rằng với mọi điểm M, ta có →MA+3→MB=4→MO.
Lời giải:
a) Do →OA+3→OB=→0 nên →OA=−3→OB do đó |→OA|=|−3||→OB|=3|→OB| hay OA = 3OB.
Ta thấy -3 < 0 nên hai vectơ →OA và →OB ngược hướng.
Do đó A và B nằm ở hai phía so với điểm O.
Ta thực hiện vẽ như sau:
Bước 1. Vẽ đường thẳng d, trên đường thẳng d xác định hai điểm O và B.
Bước 2. Trên đường thẳng d, xác định điểm A sao cho A và B nằm ở hai phía so với điểm O thỏa mãn OA = 3OB.
Ta có hình vẽ như sau:

b)
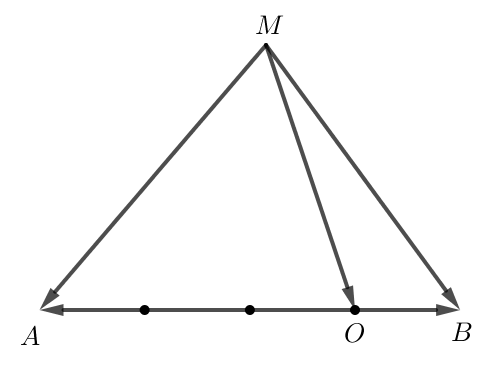
Ta có
→MA+3→MB=→MO+→OA+3(→MO+→OB)=4→MO+→OA+3→OB=4→MO.
Vậy →MA+3→MB=4→MO.
Bài 7 trang 97 Toán lớp 10 Tập 1: Cho tam giác ABC.
a) Xác định các điểm M, N, P thỏa mãn: →MB=12→BC, →AN=3→NB, →CP=→PA.
b) Biểu thị mỗi vectơ →MN, →MP theo hai vectơ →BC, →BA.
c) Chứng minh ba điểm M, N, P thẳng hàng.
Lời giải:
a) Do →MB=12→BC nên hai vectơ →MB và →BC cùng hướng.
Do đó M và C nằm ở hai phía so với điểm B sao cho MB = 12BC.
Do →AN=3→NB nên →AN+→NB=4→NB hay →AB=4→NB.
Do đó A và N nằm cùng phía so với điểm B sao cho NB = 14AB.
Do →CP=→PA nên →CP+→PA=2→PA hay →CA=2→PA.
Do đó P và C nằm cùng phía so với điểm A sao cho PA = 12CA.
Ta có hình vẽ sau:
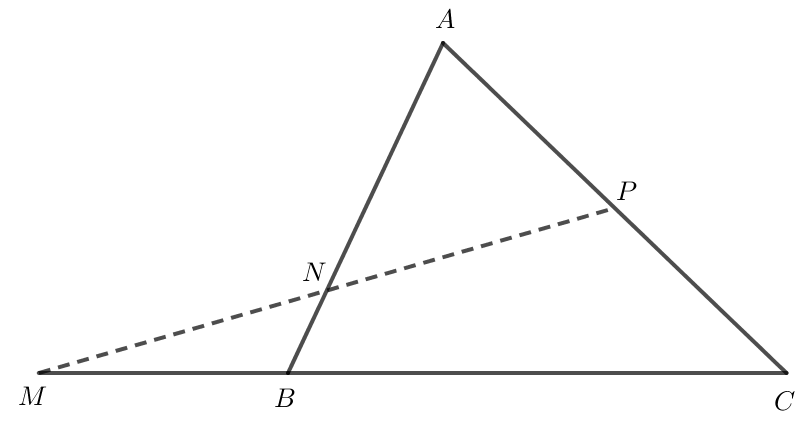
b) Ta có →MN=→BN−→BM.
Do →AN=3→NB nên →NA=3→BN⇒→BN+→NA=4→BN hay →BA=4→BN.
Do đó →BN=14→BA.
Do →MB=12→BC nên →BM=−12→BC.
Do đó →MN=→BN−→BM=14→BA+12→BC.
Ta có →MP=→BP−→BM.
Do đó P và C nằm cùng phía so với điểm A và PA = 12CA nên P là trung điểm của CA.
Do đó →BA+→BC=2→BP⇒→BP=12(→BA+→BC).
Do đó →MP=→BP−→BM=12(→BA+→BC)+12→BC=12→BA+→BC.
Ta thấy →MN=14→BA+12→BC; →MP=12→BA+→BC nên →MP=2→MN.
Do đó M, N, P thẳng hàng và N là trung điểm của MP.
Lý thuyết Toán 10 Bài 3: Tích của một số với một vectơ- Chân trời sáng tạo
1. Tích của một số với một vectơ và các tính chất
Cho số k ≠ 0 và →a≠→0. Tích của số k với →a≠→0 là một vectơ, kí hiệu là k→a.
Vectơ k→a cùng hướng với →a nếu k > 0, ngược hướng với →a nếu k < 0 và có độ dài bằng |k|.|→a|.
Ta quy ước 0→a=→0 và k→0=→0.
Người ta còn gọi tích của một số với một vectơ là tích của một vectơ với một số.
Ví dụ: Cho tam giác ABC có D, E, F lần lượt là trung điểm các cạnh AB, BC, CA. Tìm các vectơ bằng: 2→DE; −12→CA; −2→EC.
Hướng dẫn giải
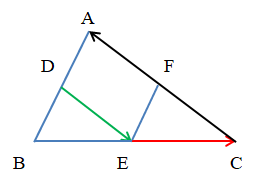
+ Vectơ bằng 2→DE:
Tam giác ABC có D, E lần lượt là trung điểm của AB, BC.
Do đó DE là đường trung bình của tam giác ABC.
Suy ra DE // AC và 2DE = AC.
Vì k = 2 > 0 nên vectơ cần tìm cùng hướng với →DE và có độ dài bằng 2DE.
Ta có →DE cùng hướng với →AC và 2DE = AC.
Do đó 2→DE=→AC.
+ Vectơ bằng −12→CA:
Ta có F là trung điểm CA.
Do đó FA = CF = 12CA.
Vì k = −12 < 0, nên vectơ cần tìm ngược hướng với →CA và có độ dài bằng 12CA.
Ta có →AF, →FC ngược hướng với →CA và AF = FC = 12CA.
Do đó →AF=→FC=−12→CA.
+ Vectơ bằng −2→EC:
Ta có E là trung điểm BC.
Do đó CB = 2EC.
Vì k = –2 < 0, nên vectơ cần tìm ngược hướng với →EC và có độ dài bằng 2EC.
Ta có →CB ngược hướng với →EC và CB = 2EC.
Do đó →CB=−2→EC.
Tính chất:
Với hai vectơ →a và →b bất kì, với mọi số thực h và k, ta có:
+) k(→a+→b)=k→a+k→b;
+) (h+k)→a=h→a+k→a;
+) h(k→a)=(hk)→a;
+) 1.→a=→a;
+) (−1).→a=−→a.
Ví dụ: Ta có:
a) 6(→x+→y)=6→x+6→y;
b) (3+x)→u=3→u+x→u;
c) 6.(−5→i)=[6.(−5)]→i=−30→i;
d) 2→c−7→c=(2−7)→c=−5→c.
Ví dụ: Cho tam giác ABC. Chứng minh G là trọng tâm của tam giác ABC khi và chỉ khi →MA+→MB+→MC=3→MG.
Hướng dẫn giải
Ta có →MA+→MB+→MC=3→MG
⇔→MG+→GA+→MG+→GB+→MG+→GC=3→MG (quy tắc ba điểm)
⇔3→MG+→GA+→GB+→GC=3→MG
⇔→GA+→GB+→GC=→0
⇔ G là trọng tâm của tam giác ABC (đpcm).
2. Điều kiện để hai vectơ cùng phương
Hai vectơ →a và →b (→b≠→0) cùng phương khi và chỉ khi có số k sao cho →a=k→b.
Nhận xét: Ba điểm phân biệt A, B, C thẳng hàng khi và chỉ khi có số k ≠ 0 để →AB=k→AC.
Chú ý: Cho hai vectơ →a và →b không cùng phương. Với mỗi →c luôn tồn tại duy nhất cặp số thực (m; n) sao cho →c=m→a+n→b.
Ví dụ: Cho tam giác ABC. Lấy các điểm M, N, P sao cho →MB=3→MC, →NA+3→NC=→0, →PA+→PB=→0.
a) Biểu diễn →MP theo →AB, →AC.
b) Biểu diễn →MN theo →AB, →AC.
c) Chứng minh rằng: 3 điểm M, N, P thẳng hàng.
Hướng dẫn giải
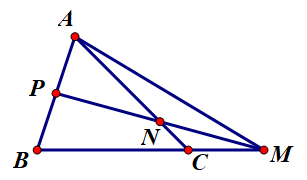
a) Ta có →MB=3→MC⇒|→MB|=|3|.|→MC|⇒MB=3MC.
Mà →MB, →MC cùng hướng (do k = 3 > 0)
Do đó ba điểm B, C, M thẳng hàng và C nằm giữa B, M sao cho MB = 3MC.
Ta có →PA+→PB=→0 nên P là trung điểm AB.
Do đó AP = 12AB.
Mà →AP, →AB cùng hướng.
Suy ra →AP=12→AB.
Ta có: →MB=→MC+→CB⇔→MB=13→MB+→CA+→AB
⇔23→MB=−→AC+→AB⇔→MB=32→AB−32→AC
Ta có
→AM=→AB+→BM=→AB−→MB=→AB−32→AB+32→AC=−12→AB+32→AC.
Ta có →MP=→AP−→AM=12→AB+12→AB−32→AC=→AB−32→AC
Vậy →MP=→AB−32→AC (1)
b) Ta có →NA+3→NC=→0⇔→NA=−3→NC.
Do đó |→NA|=|−3|.|→NC| hay NA = 3NC.
Khi đó ta có AN = 34AC.
Mà →NA, →NC ngược hướng (do k = ‒3 < 0).
Do đó ba điểm A, N, C thẳng hàng và N nằm giữa hai điểm A và C sao cho AN=34AC.
Suy ra →AN=34→AC.
Ta có →MN=→AN−→AM=34→AC+12→AB−32→AC=12→AB−34→AC
Vậy →MN=12→AB−34→AC. (2)
c) Từ (1), ta suy ra 2→MP=2→AB−3→AC.
Từ (2), ta suy ra 4→MN=2→AB−3→AC.
Do đó ta có 2→MP=4→MN hay →MP=2→MN.
Vậy ba điểm M, N, P thẳng hàng.
Xem thêm lời giải bài tập Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:
Bài 4: Tích vô hướng của hai vectơ
Bài 2: Mô tả và biểu diễn dữ liệu trên các bảng và biểu đồ
Bài 3: Các số đặc trưng đo xu thế trung tâm của mẫu số liệu
Xem thêm tài liệu Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:
Xem thêm các chương trình khác:
- Soạn văn lớp 10 (hay nhất) – Chân trời sáng tạo
- Tác giả tác phẩm Ngữ văn lớp 10 – Chân trời sáng tạo
- Soạn văn lớp 10 (ngắn nhất) – Chân trời sáng tạo
- Tóm tắt tác phẩm Ngữ văn lớp 10 – Chân trời sáng tạo
- Giải sbt Ngữ văn lớp 10 – Chân trời sáng tạo
- Bố cục tác phẩm Ngữ văn lớp 10 – Chân trời sáng tạo
- Nội dung chính tác phẩm Ngữ văn lớp 10 – Chân trời sáng tạo
- Văn mẫu lớp 10 – Chân trời sáng tạo
- Giải Chuyên đề học tập Ngữ văn 10 – Chân trời sáng tạo
- Giải sgk Tiếng Anh 10 Friends Global – Chân trời sáng tạo
- Giải sbt Tiếng Anh 10 Friends Global – Chân trời sáng tạo
- Trọn bộ Từ vựng Tiếng Anh 10 Friends Global đầy đủ nhất
- Ngữ pháp Tiếng Anh 10 Friends Global
- Giải sgk Vật lí 10 – Chân trời sáng tạo
- Giải sbt Vật lí 10 – Chân trời sáng tạo
- Lý thuyết Vật lí 10 – Chân trời sáng tạo
- Giải Chuyên đề Vật lí 10 – Chân trời sáng tạo
- Giải sgk Hóa học 10 – Chân trời sáng tạo
- Lý thuyết Hóa học 10 – Chân trời sáng tạo
- Giải sbt Hóa học 10 – Chân trời sáng tạo
- Giải Chuyên đề Hóa học 10 – Chân trời sáng tạo
- Giải sgk Sinh học 10 – Chân trời sáng tạo
- Giải sbt Sinh học 10 – Chân trời sáng tạo
- Lý thuyết Sinh học 10 – Chân trời sáng tạo
- Giải Chuyên đề Sinh học 10 – Chân trời sáng tạo
- Giải sgk Lịch sử 10 – Chân trời sáng tạo
- Giải sbt Lịch sử 10 – Chân trời sáng tạo
- Giải Chuyên đề Lịch sử 10 – Chân trời sáng tạo
- Lý thuyết Lịch sử 10 – Chân trời sáng tạo
- Giải sgk Địa lí 10 – Chân trời sáng tạo
- Lý thuyết Địa Lí 10 - Chân trời sáng tạo
- Giải sbt Địa lí 10 – Chân trời sáng tạo
- Giải Chuyên đề Địa lí 10 – Chân trời sáng tạo
- Giải sgk Giáo dục Kinh tế và Pháp luật 10 – Chân trời sáng tạo
- Giải sbt Giáo dục Kinh tế và Pháp luật 10 – Chân trời sáng tạo
- Giải Chuyên đề Kinh tế và pháp luật 10 – Chân trời sáng tạo
- Lý thuyết KTPL 10 – Chân trời sáng tạo
- Giải sgk Hoạt động trải nghiệm 10 – Chân trời sáng tạo
- Giải sbt Hoạt động trải nghiệm 10 – Chân trời sáng tạo
- Giải sgk Giáo dục thể chất 10 – Chân trời sáng tạo
