Giải Toán 10 Bài 3 (Chân trời sáng tạo): Các số đặc trưng đo xu thế trung tâm của mẫu số liệu

Giải bài tập Toán 10 Bài 3: Các số đặc trưng đo xu thế trung tâm của mẫu số liệu

Giải Toán 10 trang 112 Tập 1

Hoạt động khởi động trang 112 Toán 10 Tập 1: Sau khi đã thu thập dữ liệu về lượng nước sinh hoạt trong một tháng của từng hộ gia đình ở hai khu vực dân cư, bác Vinh muốn đánh giá xem hộ gia đình ở khu vực nào dùng hết nhiều nước sinh hoạt hơn.

Theo bạn bác Vinh nên làm thế nào?

Lời giải:

Theo em, bác Vinh đã có dữ liệu về lượng nước sinh hoạt trong một tháng của từng hộ gia đình và để so sánh xem khu vực nào dùng hết nhiều nước sinh hoạt hơn bác Vinh có thể sử dụng số trung bình, trung vị, mốt.

1. Số trung bình

Hoạt động khám phá 1 trang 112 Toán lớp 10 Tập 1: Điểm số bài kiểm tra môn Toán của các bạn trong Tổ 1 là 6; 10; 6; 8; 7; 10, còn các bạn Tổ 2 là 10; 6; 9; 9; 8; 9. Theo em, tổ nào có kết quả kiểm tra tốt hơn? Tại sao?

Lời giải:

Điểm trung bình kết quả kiểm tra của Tổ 1 là: $\overline{x_1}=\frac{6+10+6+8+7+20}{6}\approx 7,83$.

Điểm trung bình kết quả kiểm tra của Tổ 2 là: $\overline{x_2}=\frac{10+6+9+9+8+9}{6}=8,5$.

Vì 8,5 > 7,83 nên tổ 2 có kết quả kiểm tra tốt hơn Tổ 1.

Giải Toán 10 trang 114 Tập 1

Vận dụng 1 trang 114 Toán lớp 10 Tập 1: Thời gian chạy 100 mét (đơn vị: giây) của các bạn học sinh ở hai nhóm A và B được ghi lại ở bảng sau:

Nhóm nào có thành tích chạy tốt hơn?

Lời giải:

Thời gian chạy trung bình của các bạn ở nhóm A là:

$\frac{1}{8}$(12,2 + 13,5 + 12,7 + 13,1 + 12,5 + 12,9 + 13,2 + 12,8) ≈ 12,86 (giây).

Thời gian chạy trung bình của các bạn ở nhóm B là:

$\frac{1}{5}$(12,1 + 13,4 + 13,2 + 12,9 + 13,7) = 13,06 (giây).

Do 12,86 < 13,06 nên nhóm A có thành tích tốt hơn nhóm B.

Vận dụng 2 trang 114 Toán lớp 10 Tập 1: Số bàn thắng mà một đội bóng ghi được ở mỗi trận đấu trong một mùa giải được thống kê lại ở bảng sau:

Hãy xác định số bàn thắng trung bình đội đó ghi được trong một trận đấu của mùa giải.

Lời giải:

Số bàn thắng trung bình đội đó ghi được trong một trận đấu của mùa giải là:

$\frac{1.10+2.5+3.3+4.2+6.1}{5+10+5+3+2+1}$ ≈ 1,65 bàn thắng.

2. Trung vị và tứ phân vị

Hoạt động khám phá 2 trang 114 Toán lớp 10 Tập 1: Bảng sau thống kê số sách mỗi bạn học sinh Tổ 1 và Tổ 2 đã đọc ở thư viện trường trong một tháng:

a) Trung bình mỗi bạn Tổ 1 và mỗi bạn Tổ 2 đọc bao nhiêu quyển sách ở thư viện trường trong tháng đó?

b) Em hãy thảo luận với các bạn trong nhóm xem tổ nào chăm đọc sách ở thư viện hơn.

Lời giải:

a) Số sách trung bình mỗi bạn ở Tổ 1 đọc là: $\frac{3+1+2+1+2+2+3+25+1}{9}$ ≈ 4,4 quyển.

Số sách trung bình mỗi bạn ở Tổ 2 đọc là: $\frac{4+5+4+3+3+4+5+4}{8}$ = 4 quyển.

b) Ta thấy số sách trung bình mỗi bạn Tổ 1 đọc lớn hơn so với số sách trung bình mỗi bạn Tổ 2 đọc được, điều này là do ở Tổ 1 có một số liệu quá lớn so với các số liệu còn lại. Và khi quan sát vào bảng số liệu ta thấy mỗi bạn Tổ 2 đọc nhiều sách hơn số bạn Tổ 1. Do đó ở tình huống này ta không thể dùng số trung bình để so sánh độ chăm đọc sách của hai tổ.

Giải Toán 10 trang 115 Tập 1

Thực hành 1 trang 115 Toán lớp 10 Tập 1: Hãy tìm trung vị của các số liệu ở Vận dụng 1 và Vận dụng 2.

Lời giải:

+) Tại Vận dụng 1 ta có thời gian chạy 100 m (đơn vị giây) của các bạn học sinh như sau:

Sắp xếp thời gian chạy của nhóm A theo thứ tự không giảm ta được mẫu:

12,2; 12,5; 12,7; 12,8; 12,9; 13,1; 13,2; 13,5.

Cỡ mẫu bằng 8 nên trung vị của nhóm A là trung bình cộng của số liệu thứ 4 và thứ 5 của mẫu trên, tức là M_e = $\frac{1}{2}$(12,8 + 12,9) = 12,85.

Sắp xếp thời gian chạy của nhóm B theo thứ tự không giảm ta được mẫu:

12,1; 12,9; 13,2; 13,4; 13,7.

Cỡ mẫu bằng 5 nên trung vị của nhóm B là số liệu thứ 3 của mẫu trên, tức là M_e = 13,2.

+) Tại Vận dụng 2 ta có số bàn thắng của một đội bóng ở mỗi trận đấu như sau:

Sắp xếp số bàn thắng của đội bóng theo thứ tự không giảm ta được mẫu:

0; 0; 0; 0; 0; 1; 1; 1; 1; ...; 1; 2; 2; 2; 2; 2; 3; 3; 3; 4; 4; 6 (trong dãy số này có 10 số 1).

Cỡ mẫu bằng 26 nên trung vị của số bàn thắng là trung bình cộng của số liệu thứ 13 và thứ 14 của mẫu trên, tức là M_e = $\frac{1}{2}$(1 + 1) = 1.

Giải Toán 10 trang 116 Tập 1

Hoạt động khám phá 3 trang 116 Toán lớp 10 Tập 1: Cân nặng của 20 vận động viên môn vật của một câu lạc bộ được ghi lại ở bảng sau:

Để thuận tiện cho việc luyện tập, ban huấn luyện muốn xếp 20 vận động viên trên thành 4 nhóm, mỗi nhóm gồm 25% số vận động viên có cân nặng gần nhau. Bạn hãy giúp ban huấn luyện xác định các ngưỡng cân nặng để phân nhóm mỗi vận động viên.

Lời giải:

Sắp xếp cân nặng của 20 vận động viên trên theo thứ tự không giảm ta được:

50; 52; 52; 54; 54; 56; 56; 57; 58; 58; 59; 61; 61; 62; 64; 65; 66; 67; 68; 69.

Cỡ mẫu bằng 20 nên trung vị của cân nặng 20 vận động viên bằng trung bình cộng số liệu thứ 10 và 11 của mẫu trên, tức là M_e = $\frac{1}{2}$(58 + 59) = 58,5.

Chia 20 vận động viên đã sắp xếp trên thành 4 nhóm có 5 vận động viên.

Nhóm 1: 50; 52; 52; 54; 54.

Nhóm 2: 56; 56; 57; 58; 58.

Nhóm 3: 59; 61; 61; 62; 64.

Nhóm 4: 65; 66; 67; 68; 69.

Khi đó ta có các ngưỡng sau:

Ngưỡng giữa nhóm 1 và nhóm 2 là (54 + 56) : 2 = 55.

Ngưỡng giữa nhóm 2 và nhóm 3 là (58 + 59) : 2 = 58,5.

Ngưỡng giữa nhóm 3 và nhóm 4 là (64 + 65) : 2 = 64,5.

Vậy các ngưỡng cân nặng để phân nhóm vận động viên là 55 kg, 58,5 kg, 64,5 kg.

Giải Toán 10 trang 117 Tập 1

Thực hành 2 trang 117 Toán lớp 10 Tập 1: Hãy tìm tứ phân vị của các mẫu số liệu sau:

a) 10; 13; 15; 2; 10; 19; 2; 5; 7.

b) 15; 19; 10; 5; 9; 10; 1; 2; 5; 15.

Lời giải:

a) Sắp xếp lại mẫu theo thứ tự không giảm ta được mẫu: 2; 2; 5; 7; 10; 10; 13; 15; 19.

Vì cỡ mẫu bằng 9, là số lẻ nên giá trị tứ phân vị thứ hai là Q₂ = 10.

Tứ phân vị thứ nhất là trung vị của mẫu 2; 2; 5; 7. Do đó Q₁ = $\frac{1}{2}$(2 + 5) = 3,5.

Tứ phân vị thứ ba là trung vị của mẫu 10; 13; 15; 19. Do đó Q₃ = $\frac{1}{2}$(13 + 15) = 14.

b) Sắp xếp lại mẫu theo thứ tự không giảm ta được mẫu: 1; 2; 5; 5; 9; 10; 10; 15; 15; 19.

Vì cỡ mẫu bằng 10, là số chẵn nên giá trị tứ phân vị thứ hai là Q₂ = $\frac{1}{2}$(9 + 10) = 9,5.

Tứ phân vị thứ nhất là trung vị của mẫu 1; 2; 5; 5; 9. Do đó Q₁ = 5.

Tứ phân vị thứ ba là trung vị của mẫu 10; 10; 15; 15; 19. Do đó Q₃ = 15.

3. Mốt

Hoạt động khám phá 4 trang 117 Toán lớp 10 Tập 1: Một cửa hàng kinh doanh hoa thống kê số hoa hồng bán được trong ngày 14 tháng 2 theo loại hoa và thu được bảng tần số sau:

Cửa hàng nên nhập loại hoa hồng nào nhiều nhất để bán trong ngày 14 tháng 2 năm tiếp theo? Tại sao?

Lời giải:

Ta thấy hoa hồng nhung bán được nhiều nhất.

Do đó cửa hàng nên nhập loại hoa hồng nhung để bán trong ngày 14 tháng 2 năm tiếp theo.

Thực hành 3 trang 117 Toán lớp 10 Tập 1: Hãy tìm mốt của số liệu điểm kiểm tra của các bạn Tổ 1 trong Hoạt động khám phá 1.

Lời giải:

Điểm số bài kiểm tra môn Toán của các bạn trong Tổ 1 là 6; 10; 6; 8; 7; 10.

Ta thấy số bài đạt điểm 6 có 2 bài, số bài đạt điểm 7 và 8 có 1 bài, số bài đạt điểm 10 có 2 bài.

Do đó mốt của số liệu điểm kiểm tra của các bạn Tổ 1 là 6 và 10.

Bài tập

Giải Toán 10 trang 118 Tập 1

Bài 1 trang 118 Toán lớp 10 Tập 1: Hãy tìm số trung bình, tứ phân vị và mốt của các mẫu số liệu sau:

a) 23; 41; 71; 29; 48; 45; 72; 41.

b) 12; 32; 93; 78; 24; 12; 54; 66; 78.

Lời giải:

a) Số trung bình cộng của mẫu trên là:

$\frac{1}{8}$(23 + 41 + 71 + 29 + 48 + 45 + 72 + 41) = 46,25.

Sắp xếp mẫu số liệu trên theo thứ tự không giảm ta được:

23; 29; 41; 41; 45; 48; 71; 72.

Do cỡ mẫu bằng 8, là số chẵn nên tứ phân vị thứ hai là Q₂ = $\frac{1}{2}$(41 + 45) = 43.

Tứ phân vị thứ nhất là trung vị của mẫu 23; 29; 41; 41 là Q₁ = $\frac{1}{2}$(29 + 41) = 35.

Tứ phân vị thứ ba là trung vị của mẫu 45; 48; 71; 72 là Q₁ = $\frac{1}{2}$(48 + 71) = 59,5.

Trong mẫu số liệu trên, số xuất hiện nhiều nhất là 41 nên mốt của mẫu số liệu trên là 41.

b) Số trung bình cộng của mẫu trên là:

$\frac{1}{9}$(12 + 32 + 93 + 78 + 24 + 12 + 54 + 66 + 78) ≈ 49,89.

Sắp xếp mẫu số liệu trên theo thứ tự không giảm ta được:

12; 12; 24; 32; 54; 66; 78; 78; 93.

Do cỡ mẫu bằng 9, là số lẻ nên tứ phân vị thứ hai là Q₂ = 54.

Tứ phân vị thứ nhất là trung vị của mẫu 12; 12; 24; 32 là Q₁ = $\frac{1}{2}$(12 + 24) = 18.

Tứ phân vị thứ ba là trung vị của mẫu 66; 78; 78; 93 là Q₁ = $\frac{1}{2}$(78 + 78) = 78.

Trong mẫu số liệu trên, số xuất hiện nhiều nhất là 12 và 78 nên mốt của mẫu số liệu trên là 12 và 78.

Bài 2 trang 118 Toán lớp 10 Tập 1: Hãy tìm số trung bình, tứ phân vị và mốt của các mẫu số liệu sau:

a)

b)

Lời giải:

a) Số trung bình của mẫu số liệu là:

$\frac{23.6+25.8+28.10+31.6+33.4+37.3}{6+8+10+6+4+3}$ ≈ 28,3.

Sắp xếp các giá trị theo thứ tự không giảm ta được mẫu:

23; 23; 23; 23; 23; 23; 25; 25; 25; 25; 25; 25; 25; 25; 28; 28; 28; 28; 28; 28; 28; 28; 28; 28; 31; 31; 31; 31; 31; 31; 33; 33; 33; 33; 37; 37; 37.

Cỡ mẫu bằng 37, là số lẻ nên tứ phân vị thứ hai là số liệu thứ 19 là Q₂ = 28.

Tứ phân vị thứ nhất là trung vị của mẫu 23; 23; 23; 23; 23; 23; 25; 25; 25; 25; 25; 25; 25; 25; 28; 28; 28; 28 với cỡ mẫu 18 là số chẵn nên trung vị là trung bình cộng của số liệu thứ 9 và thứ 10 trong mẫu là Q₁ = $\frac{1}{2}$(25 + 25) = 25.

Tứ phân vị thứ ba là trung vị của mẫu 28; 28; 28; 28; 28; 31; 31; 31; 31; 31; 31; 33; 33; 33; 33; 37; 37; 37 với cỡ mẫu bằng 18 là số chẵn nên trung vị của mẫu là trung bình cộng của số liệu thứ 9 và thứ 10 là $\frac{1}{2}$(31 + 31) = 31.

Do đó tứ phân vị thứ ba của mẫu số liệu là Q₃ = 31.

Giá trị 28 xuất hiện nhiều nhất (10 lần) nên mốt của dấu hiệu trên là M₀ = 28.

b) Số trung bình của mẫu số liệu là:

$\frac{2.0,2+4.0,1+5.0,1}{0,6+0,2+0,1+0,1}$ = 1,3.

Chọn cỡ mẫu bằng 10, khi đó tần số của 0 là 0,6 . 10 = 6; tần số của 1 là 0,2 . 10 = 2, tần số của 4 là 0,1 . 10 = 1, tần số của 5 là 0,1 . 10 = 1.

Sắp xếp các giá trị theo thứ tự không giảm ta được mẫu:

0; 0; 0; 0; 0; 0; 2; 2; 4; 5.

Cỡ mẫu bằng 10, là số chẵn nên tứ phân vị thứ hai bằng trung bình cộng của số liệu thứ 5 và số liệu thứ 6 trong mẫu là Q₂ = $\frac{1}{2}$(0 + 0) = 0.

Tứ phân vị thứ nhất là trung vị của mẫu 0; 0; 0; 0; 0 với cỡ mẫu bằng 5 là số liệu thứ 3 trong mẫu là Q₁ = 0.

Tứ phân vị thứ ba là trung vị của mẫu 0; 2; 2; 4; 5 với cỡ mẫu bằng 5 là số liệu thứ 8 trong mẫu là Q₃ = 2.

Giá trị 0 xuất hiện nhiều nhất nên mốt của dấu hiệu trên là M₀ = 0.

Bài 3 trang 118 Toán lớp 10 Tập 1: An lấy ra ngẫu nhiên 3 quả bóng từ một hộp có chứa nhiều bóng xanh và bóng đỏ. An đếm xem có bao nhiêu bóng đỏ trong 3 bóng lấy ra rồi trả bóng lại hộp. An lặp lại phép thử trên 100 lần và ghi lại kết quả ở bảng sau:

Hãy tìm số trung bình, tứ phân vị và mốt của bảng kết quả trên.

Lời giải:

Số trung bình của bảng kết quả trên là:

$\frac{1.30+2.40+3.20}{10+30+40+20}$ = 1,7.

Cỡ mẫu bằng 100 nên tứ phân vị thứ hai là trung bình cộng của số liệu thứ 50 và 51 trong mẫu là Q₂ = $\frac{1}{2}$(2 + 2) = 2.

Tứ phân vị thứ nhất là trung vị của mẫu 0; 1; 2 với cỡ mẫu là 50 bằng trung bình cộng của số liệu thứ 25 và 26 của mẫu dữ liệu là Q₁ = $\frac{1}{2}$(1 + 1) = 1.

Tứ phân vị thứ ba là trung vị của mẫu 1; 2; 3 với cỡ mẫu là 50 bằng trung bình cộng của số liệu thứ 75 và 76 của mẫu dữ liệu là Q₃ = $\frac{1}{2}$(2 + 2) = 2.

Giá trị 2 xuất hiện nhiều nhất nên mốt của bảng kết quả trên là 2.

Bài 4 trang 118 Toán lớp 10 Tập 1: Trong một cuộc thi nghề, người ta ghi lại thời gian hoàn thành một sản phẩm của một số thí sinh ở bảng sau:

a) Hãy tìm số trung bình, tứ phân vị và mốt của thời gian thi nghề của các thí sinh trên.

b) Năm ngoái, thời gian thi của các thí sinh có số trung bình và trung vị đều bằng 7. Bạn hãy so sánh thời gian thi nói chung của các thí sinh trong hai năm.

Lời giải:

a) Số trung bình cộng về thời gian thi nghề của các thí sinh là:

$\frac{5.1+6.3+7.5+8.2+35.1}{1+3+5+2+1}$ ≈ 9,08.

Cỡ mẫu bằng 12 nên tứ phân vị thứ hai bằng trung bình cộng của số liệu thứ 6 và thứ 7 trong mẫu là Q₂ = $\frac{1}{2}$(7 + 7) = 7.

Tứ phân vị thứ nhất là trung vị của mẫu 5; 6; 6; 6; 7; 7 với cỡ mẫu là 6 bằng trung bình cộng của số liệu thứ 3 và thứ 4 trong mẫu là Q₁ = $\frac{1}{2}$(6 + 6) = 6.

Tứ phân vị thứ ba là trung vị của mẫu 7; 7; 7; 8; 8; 35 với cỡ mẫu là 6 bằng trung bình cộng của số liệu thứ 9 và 10 trong mẫu là Q₃ = $\frac{1}{2}$(7 + 8) = 7,5.

Giá trị 7 xuất hiện nhiều nhất nên mốt của thời gian thi nghề của các thí sinh là 7.

b) Năm ngoái, thời gian thi của các thí sinh có số trung bình và trung vị đều bằng 7.

Năm nay, thời gian thi của các thí sinh có số trung bình bằng 9,08 và trung vị bằng 7.

Do đó thời gian thi của các thí sinh năm nay nhiều hơn thời gian thi của các thí sinh năm ngoái.

Bài 5 trang 118 Toán lớp 10 Tập 1: Bác Dũng và bác Thu ghi lại số cuộc điện thoại mà mỗi người gọi mỗi ngày trong 10 ngày được lựa chọn ngẫu nhiên từ tháng 01/2021 ở bảng sau:

a) Hãy tìm số trung bình, tứ phân vị và mốt của số cuộc điện thoại mà mỗi bác gọi theo số liệu trên.

b) Nếu so sánh theo số trung bình thì ai có nhiều cuộc điện thoại hơn?

c) Nếu so sánh theo số trung vị thì ai có nhiều cuộc điện thoại hơn?

d) Theo bạn, nên dùng số trung bình hay số trung vị để so sánh xem ai có nhiều cuộc gọi điện thoại hơn mỗi ngày?

Lời giải:

a) Số trung bình về số cuộc điện thoại bác Dũng gọi là:

$\frac{1}{10}$(2 + 7 + 3 + 6 + 1 + 4 + 1 + 4 + 5 + 1) = 3,4.

Sắp xếp mẫu trên theo thứ tự không giảm ta được mẫu:

1; 1; 1; 2; 3; 4; 4; 5; 6; 7.

Cỡ mẫu bằng 10 nên tứ phân vị thứ hai là Q₂ = $\frac{1}{2}$(3 + 4) = 3,5.

Tứ phân vị thứ nhất là trung vị của mẫu 1; 1; 1; 2; 3 là Q₁ = 1.

Tứ phân vị thứ ba là trung vị của mẫu 4; 4; 5; 6; 7 là Q₃ = 5.

Số trung bình về số cuộc điện thoại của bác Thu là:

$\frac{1}{10}$(1 + 3 + 1 + 2 + 3 + 4 + 1 + 2 + 20 + 2) = 3,9.

Sắp xếp mẫu trên theo thứ tự không giảm ta được mẫu:

1; 1; 1; 2; 2; 2; 3; 3; 4; 20.

Cỡ mẫu bằng 10 nên tứ phân vị thứ hai là Q₂ = $\frac{1}{2}$(2 + 2) = 2.

Tứ phân vị thứ nhất là trung vị của mẫu 1; 1; 1; 2; 2 là Q₂ = 1.

Tứ phân vị thứ ba là trung vị của mẫu 2; 3; 3; 4; 20 là Q₃ = 3.

b) Nếu so sánh theo số trung bình thì bác Thu có nhiều cuộc điện thoại mỗi ngày hơn bác Dũng.

c) Nếu so sánh theo số trung vị thì bác Dũng có nhiều cuộc điện thoại mỗi ngày hơn bác Thu.

d) Trong mẫu số liệu của bác Thu có một số liệu quá lớn so với các số liệu khác, do đó nên sử dụng số trung vị để so sánh số cuộc điện thoại mỗi ngày của hai người.

Giải Toán 10 trang 119 Tập 1

Bài 6 trang 119 Toán lớp 10 Tập 1: Tổng số điểm mà các thành viên đội tuyển Olympic Toán quốc tế (IMO) của Việt Nam đạt được trong 20 kì thi được cho ở bảng sau:

Có ý kiến cho rằng điểm thi của đội tuyển giai đoạn 2001 – 2010 cao hơn giai đoạn 2011 – 2020. Hãy sử dụng số trung bình và trung vị để kiểm nghiệm xem ý kiến trên có đúng không?

Lời giải:

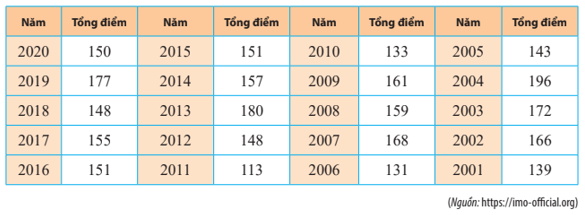
Điểm thi của đội tuyển giai đoạn 2001 - 2010 tạo thành mẫu sau:

139; 166; 172; 196; 143; 131; 168; 159; 161; 133.

Sắp xếp mẫu trên theo thứ tự không giảm ta được:

131; 133; 139; 143; 159; 161; 166; 168; 172; 196.

Số trung bình về điểm thi của đội tuyển giai đoạn 2001 - 2010 là:

$\frac{1}{10}$(131 + 133 + 139 + 143 + 159 + 161 + 166 + 168 + 172 + 196) = 156,8.

Cỡ mẫu bằng 10 nên trung vị của mẫu trên là $\frac{1}{2}$(159 + 161) = 160.

Điểm thi của đội tuyển giai đoạn 2011 - 2020 tạo thành mẫu sau:

113; 148; 180; 157; 151; 151; 155; 148; 177; 150.

Sắp xếp mẫu trên theo thứ tự không giảm ta được:

113; 148; 148; 150; 151; 151; 155; 157; 177; 180.

Số trung bình về điểm thi của đội tuyển giai đoạn 2011 - 2020 là:

$\frac{1}{10}$(113 + 148 + 148 + 150 + 151 + 151 + 155 + 157 + 177 + 180) = 153.

Cỡ mẫu bằng 10 nên trung vị của mẫu trên là $\frac{1}{2}$(151 + 151) = 151.

Ta thấy dựa vào số trung bình và trung vị thì điểm của giai đoạn 2001 - 2010 đều lớn hơn điểm của giai đoạn 2011 - 2020 nên ý kiến trên đúng.

Bài 7 trang 119 Toán lớp 10 Tập 1: Kết quả bài kiểm tra giữa kì của các bạn học sinh lớp 10A, 10B, 10C được thống kê ở các biểu đồ dưới đây.

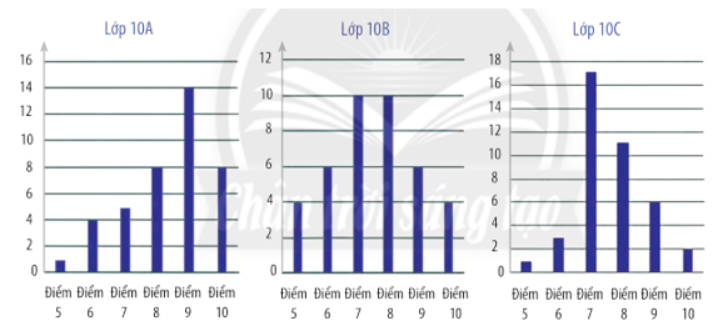
a) Hãy lập bảng thống kê số lượng học sinh theo điểm số ở mỗi lớp.

b) Hãy so sánh điểm số của học sinh các lớp đó theo số trung bình, trung vị và mốt.

Lời giải:

a) Bảng thống kê số lượng học sinh theo điểm số của lớp 10A:

Bảng thống kê số lượng học sinh theo điểm số của lớp 10B:

Bảng thống kê số lượng học sinh theo điểm số của lớp 10C:

b) Số trung bình về điểm số của lớp 10A là:

$\frac{5.1+6.4+7.5+8.8+9.14+10.8}{1+4+5+8+14+8}$ = 8,35.

Cỡ mẫu bằng 40 nên trung vị của mẫu số liệu trên bằng trung bình cộng giữa số liệu thứ 20 và 21 là $\frac{1}{2}$(9 + 9) = 9.

Mẫu số liệu trên có giá trị 9 xuất hiện nhiều nhất nên mốt của mẫu số liệu trên là 9.

Số trung bình về điểm số của lớp 10B là:

$\frac{5.4+6.6+7.10+8.10+9.6+10.4}{4+6+10+10+6+4}$ = 7,5.

Cỡ mẫu bằng 40 nên trung vị của mẫu số liệu trên bằng trung bình cộng giữa số liệu thứ 20 và 21 là $\frac{1}{2}$(7 + 8) = 7,5.

Mẫu số liệu trên có hai giá trị 7 và 8 xuất hiện nhiều nhất nên mốt của mẫu số liệu trên là 7 và 8.

Số trung bình về điểm số của lớp 10C là:

$\frac{5.1+6.3+7.17+8.11+9.6+10.2}{1+3+17+11+6+2}$ = 7,6.

Cỡ mẫu bằng 40 nên trung vị của mẫu số liệu trên bằng trung bình cộng giữa số liệu thứ 20 và 21 là $\frac{1}{2}$(7 + 7) = 7.

Mẫu số liệu trên có giá trị 7 xuất hiện nhiều nhất nên mốt của mẫu số liệu trên là 7.

Dựa vào số trung bình ta thấy 8,35 > 7,6 > 7,5.

Do đó dựa vào số trung bình thì điểm số lớp 10A cao hơn điểm số lớp 10C và điểm số lớp 10C cao hơn điểm số lớp 10B.

Dựa vào số trung vị ta thấy 9 > 7,5 > 7 nên nếu dựa vào số trung vị thì điểm số lớp 10A cao hơn điểm số lớp 10B và điểm số lớp 10B cao hơn điểm số lớp 10C.

Dựa vào mốt ta thấy 9 > 8 > 7.

Do đó dựa vào số trung bình thì điểm số lớp 10A cao hơn điểm số lớp 10B và điểm số lớp 10B cao hơn điểm số lớp 10C.

Lý thuyết Toán 10 Bài 3: Các số đặc trưng đo xu thế trung tâm của mẫu số liệu - Chân trời sáng tạo

1. Số trung bình

1.1. Công thức tính số trung bình

• Giả sử ta có một mẫu số liệu là x₁, x­₂, …, x_n.

Số trung bình (hay số trung bình cộng) của mẫu số liệu này, kí hiệu là $\overline{x}$ , được tính bởi công thức

$\overline{x}=\frac{x_1+x_2+\mathrm{...}+x_n}{n}$.

• Giả sử mẫu số liệu được cho dưới dạng bảng tần số

Khi đó, công thức tính số trung bình trở thành

$\overline{x}=\frac{n_1{x}_1+n_2{x}_2+\mathrm{...}+n_k{x}_k}{n}$.

Trong đó n = n₁ + n₂ + … + n_k. Ta gọi n là cỡ mẫu.

Chú ý: Nếu kí hiệu $f_k=\frac{n_k}{n}$ là tần số tương đối (hay còn gọi là tần suất) của x_k­ trong mẫu số liệu thì số trung bình còn có thể biểu diễn là: $\overline{x}=f_1{x}_1+f_2{x}_2+\mathrm{...}+f_k{x}_k$.

Ví dụ: Điểm số bài thực hành môn Toán của các bạn học sinh trong nhóm A là 10; 5; 7; 9; 8; 6, còn của các bạn nhóm B là 9; 9; 8; 7; 6; 8. Tính điểm trung bình của mỗi nhóm.

Hướng dẫn giải

Điểm trung bình của nhóm A là: $\frac{1}{6}\left(10+5+7+9+8+6\right)=7,5$ .

Điểm trung bình của nhóm B là: $\frac{1}{6}\left(9+9+8+7+6+8\right)\approx 7,83$ .

1.2.Ý nghĩa của số trung bình

Số trung bình của mẫu số liệu được dùng làm đại diện cho các số liệu của mẫu. Nó là một số đo xu thế trung tâm của mẫu đó.

Ví dụ: Ở trong Ví dụ thuộc phần 1.1. trên, ta thấy điểm số trung bình của nhóm B cao hơn nhóm A (7,83 > 7,5), ta có thể nói rằng thành tích thực hành của nhóm B tốt hơn nhóm A.

2. Trung vị và tứ phân vị

2.1. Trung vị

2.1.1 Định nghĩa và cách tính số trung vị

Khi các số liệu trong mẫu số liệu chênh lệch nhau quá lớn, ta dùng một đặc trưng khác của mẫu số liệu, gọi là trung vị để so sánh các mẫu số liệu với nhau.

Trung vị được định nghĩa như sau:

Sắp xếp mẫu số liệu theo thứ tự không giảm, ta được:

x₁ ≤ x₂ ≤ … ≤ x_n.

Trung vị của mẫu, kí hiệu là M_e, là giá trị ở chính giữa dãy x₁, x­­₂, …, x_n. Cụ thể:

- Nếu n = 2k + 1, (tức n là số tự nhiên lẻ), thì trung vị của mẫu M_e = x_{k + 1}.

- Nếu n = 2k, (tức n là số tự nhiên chẵn), thì trung vị của mẫu M_e = $\frac{1}{2}\left(x_k+x_{k+1}\right)$ .

Ví dụ: Tính các trung vị của điểm thực hành môn Toán của các bạn học sinh trong nhóm A và nhóm B trong Ví dụ thuộc phần 1.1.

Hướng dẫn giải

+ Sắp xếp điểm số của mỗi bạn trong nhóm A theo thứ tự không giảm, ta được:

5; 6; 7; 8; 9; 10

Vì cỡ mẫu bằng 6 nên trung vị của nhóm A là trung bình cộng của số liệu thứ 3 và thứ 4 của dãy trên, tức là M_e = $\frac{1}{2}\left(7+8\right)=7,5$ .

+ Sắp xếp điểm số của mỗi bạn trong nhóm B theo thứ tự không giảm, ta được:

6; 7; 8; 8; 9; 9

Vì cỡ mẫu bằng 6 nên trung vị của nhóm B là trung bình cộng của số liệu thứ 3 và thứ 4 của dãy trên, tức là M_e = $\frac{1}{2}\left(8+8\right)=8$ .

2.1.2 Ý nghĩa của số trung vị

Trung vị được dùng để đo xu thế trung tâm của mẫu số liệu. Trung vị là giá trị nằm ở chính giữa của mẫu số liệu theo nghĩa: luôn có ít nhất 50% số liệu trong mẫu lớn hơn hoặc bằng trung vị và ít nhất 50% số liệu trong mẫu nhỏ hơn hoặc bằng trung vị. Khi trong mẫu xuất hiện thêm một giá trị rất lớn hoặc rất nhỏ thì số trung bình sẽ bị thay đổi đáng kể nhưng trung vị thì ít thay đổi.

Ví dụ: Bảng sau thống kê số sách mỗi bạn học sinh Tổ 1 và Tổ 2 đã đọc ở thư viện trường trong một tháng:

a) Trung bình mỗi bạn Tổ 1 và mỗi bạn Tổ 2 đọc bao nhiêu quyển sách ở thư viện trường trong tháng đó?

b) Em hãy thảo luận với các bạn trong nhóm xem tổ nào chăm đọc sách ở thư viện hơn.

Hướng dẫn giải

a) Trung bình mỗi bạn Tổ 1 đọc số quyển sách ở thư viện trong tháng trên là:

$\frac{3+1+2+1+2+2+3+25+1}{9}=\frac{40}{9}\approx 4,4$.

Trung bình mỗi bạn Tổ 2 đọc số quyển số ở thư viện trong tháng trên là:

$\frac{4+5+4+3+3+4+5+4}{8}=\frac{32}{8}=4$.

b) Vì 4,4 > 4 nên theo số trung bình, các bạn Tổ 1 đọc sách chăm hơn.

Nếu dựa vào số trung bình để đánh giá xem tổ nào chăm đọc sách hơn trong bài này thì không phù hợp, do có một số liệu trong mẫu số liệu của Tổ 1 quá lớn so với các số liệu còn lại. Ta sử dụng trung vị để so sánh độ chăm học giữa hai tổ.

+ Sắp xếp mẫu số liệu theo thứ tự không giảm của Tổ 1:

1; 1; 1; 2; 2; 2; 3; 3; 25

Vì cỡ mẫu n₁ = 9 là số lẻ, nên trung vị của mẫu số liệu Tổ 1 là M_e1 = 2.

+ Sắp xếp mẫu số liệu theo thứ tự không giảm của Tổ 2:

3; 3; 4; 4; 4; 4; 5; 5

Vì cỡ mẫu n₂ = 8 là số chẵn, nên trung vị của mẫu số liệu Tổ 2 là M_e2 = $\frac{1}{2}\left(4+4\right)=4$ .

Do đó ta có: M_e2 > M_e1.

Vậy theo trung vị, các bạn Tổ 2 chăm đọc sách ở thư viện hơn Tổ 1.

2.2. Tứ phân vị

• Trung vị chia mẫu thành hai phần. Trong thực tế người ta cũng quan tâm đến trung vị của mỗi phần đó. Ba trung vị này được gọi là tứ phân vị của mẫu.

Sắp xếp mẫu số liệu theo thứ tự không giảm, ta được:

x₁ ≤ x₂ ≤ … ≤ x_n.

Tứ phân vị của một mẫu số liệu gồm ba giá trị, gọi là tứ phân vị thứ nhất, thứ hai và thứ ba (lần lượt kí hiệu là Q₁, Q₂, Q­₃). Ba giá trị này chia tập hợp dữ liệu đã sắp xếp thành bốn phần đều nhau. Cụ thể:

- Giá trị tứ phân vị thứ hai, Q₂, chính là số trung vị của mẫu.

- Giá trị tứ phân vị thứ nhất, Q₁, là trung vị của nửa số liệu đã sắp xếp bên trái Q₂ (không bao gồm Q₂ nếu n lẻ).

- Giá trị tứ phân vị thứ ba, Q₃, là trung vị của nửa số liệu đã sắp xếp bên phải Q₂ (không bao gồm Q₂ nếu n lẻ).

• Ý nghĩa của tứ phân vị

Các điểm tứ phân vị Q₁, Q₂, Q₃ chia mẫu số liệu đã sắp xếp theo thứ tự từ nhỏ đến lớn thành bốn phần, mỗi phần chia khoảng 25% tổng số liệu đã thu thập được.

Tứ phân vị thứ nhất Q₁ còn được gọi là tứ phân vị dưới và đại diện cho nửa mẫu số liệu phía dưới. Tứ phân vị thứ ba Q₃, còn được gọi là tứ phân vị trên và đại diện cho nửa mẫu số liệu ở phía trên.

Ví dụ: Tìm tứ phân vị của mẫu số liệu sau: 3; 5; 6; 13; 25; 17; 19.

Hướng dẫn giải

Sắp xếp các số liệu theo thứ tự không giảm ta được:

3; 5; 6; 13; 17; 19; 25.

Vì cỡ mẫu n = 7, là số lẻ, nên giá trị tứ phân vị thứ hai là Q₂ = 13.

Tứ phân vị thứ nhất là trung vị của mẫu: 3; 5; 6. Do đó Q₁ = 5.

Tứ phân vị thứ ba là trung vị của mẫu: 17; 19; 25. Do đó Q₃ = 19.

3. Mốt

Cho mẫu số liệu dưới dạng bảng tần số. Giá trị có tần số lớn nhất được gọi là mốt của mẫu số liệu và kí hiệu là M_o.

Ý nghĩa của mốt: Mốt đặc trưng cho giá trị xuất hiện nhiều nhất trong mẫu.

Chú ý: Một mẫu số liệu có thể có rất nhiều mốt. Khi tất cả các giá trị trong mẫu số liệu có tần số xuất hiện bằng nhau thì mẫu số liệu đó không có mốt.

Ví dụ: Cho mẫu số liệu:

Ta thấy giá trị 35 có tần số lớn nhất, do đó, mốt của mẫu số liệu trên là M_o = 35.

Xem thêm lời giải bài tập Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:

Bài 4: Các số đặc trưng đo mức độ phân tán của mẫu số liệu

Bài tập cuối chương 6

Bài 1: Dùng máy tính cầm tay để tính toán với số gần đúng và tính các số đặc trưng của mẫu số liệu thống kê

Bài 2: Dùng bảng tính để tính các số đặc trưng của mẫu số liệu thống kê

Bài 1: Mệnh đề

Xem thêm tài liệu Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:

Lý thuyết Bài 3: Các số đặc trưng đo xu thế trung tâm của mẫu số liệu