Giải Toán 10 Bài 1 (Chân trời sáng tạo): Quy tắc cộng và quy tắc nhân

Giải bài tập Toán 10 Bài 1: Quy tắc cộng và quy tắc nhân

A. Câu hỏi

Giải Toán 10 trang 20 Tập 2

Hoạt động khởi động trang 20 Toán lớp 10 Tập 2:

Một công ty dự kiến tạo các mã số nhân viên, mỗi mã số có ba kí tự gồm một chữ cái tiếng Anh viết hoa đứng trước hai chữ số. Tuy nhiên họ đang băn khoăn rằng số mã số như vậy có đủ để cấp cho mỗi nhân viên của họ một mã số riêng hay không.Họ cần làm gì để biết được điều đó?

Lời giải:

Với những điều kiện đã đặt ra, công ty cần tính toán xem sẽ tạo được bao nhiêu mã số và so sánh với số nhân viên của công ty. Cách tính toán số mã số thẻ cho nhân viên sẽ được tìm hiểu trong bài học hôm nay.

Hoạt động khám phá 1 trang 20 Toán lớp 10 Tập 2:

Trong một cửa hàng bán kem có 5 loại kem que và 4 loại kem ốc quế như Hình 1. Có bao nhiêu cách chọn mua một loại kem que hoặc kem ốc quế ở cửa hàng này?

Lời giải:

Để mua một loại kem tại cửa hàng này ta có thể có hai lựa chọn hoặc mua kem que hoặc mua kem ốc quế:

Lựa chọn thứ nhất: Chọn mua một kem que, có 5 cách chọn.

Lựa chọn thứ hai: Chọn mua một kem ốc quế, có 4 cách chọn.

Vậy có tất cả 5 + 4 = 9 lựa chọn cho việc mua một loại kem ở cửa hàng.

Giải Toán 10 trang 21 Tập 2

Thực hành 1 trang 21 Toán lớp 10 Tập 2:

Hà có 5 cuốn sách khoa học, 4 cuốn tiểu thuyết và 3 cuốn truyện tranh (các sách khác nhau từng đôi một). Hà đồng ý cho Nam mượn một cuốn sách trong số đó để đọc. Nam có bao nhiêu cách chọn một cuốn sách để mượn.

Lời giải:

Việc Hà cho Nam mượn một quyển sách có 3 phương án để thực hiện:

Phương án 1: Cho mượn một quyển sách khoa học, có 5 cách chọn.

Phương án 2: Cho mượn một quyển tiểu thuyết, có 4 cách chọn.

Phương án 3: Cho mượn một quyển truyện tranh, có 3 cách chọn.

Áp dụng quy tắc cộng, ta có số cách chọn để Hà cho Nam mượn một quyển sách là:

5 + 4 + 3 = 12 (cách).

Vậy Nam có 12 cách để mượn Hà 1 quyển sách.

Hoạt động khám phá 2 trang 21 Toán lớp 10 Tập 2:

An có 3 chiếc áo và 4 chiếc quần thể thao. An muốn chọn một bộ quần áo trong số đó để mặc chơi thể thao cuối tuần này.

a) Vẽ vào vở và hoàn thành sơ đồ hình cây như Hình 4 để thể hiện tất cả các khả năng mà An có thể lựa chọn một bộ quần áo

b) An có bao nhiêu cách lựa chọn bộ quần áo? Hãy giải thích?

Lời giải:

a)

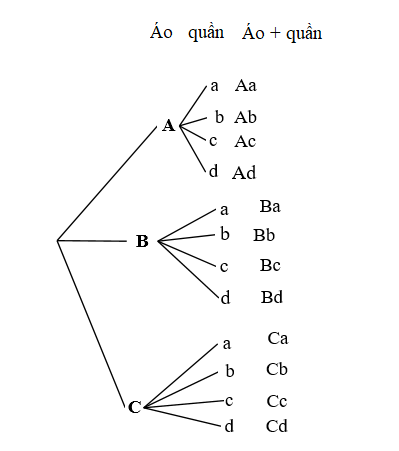
b) Dựa vào sơ đồ trên ta thấy công việc chọn áo quần của bạn An được chia thành 2 giai đoạn:

+ Giai đoạn thứ nhất: Chọn một chiếc áo, có 3 cách chọn

+ Giai đoạn thứ hai: Ứng với mỗi cách chọn chiếc áo có 4 cách chọn chiếc quần tương ứng.

Theo sơ đồ trên ta thấy có tất cả 12 cách lựa chọn bộ quần áo hay chính là tích của số lựa chọn của giai đoạn thứ nhất và giai đoạn thứ hai.

Giải Toán 10 trang 24 Tập 2

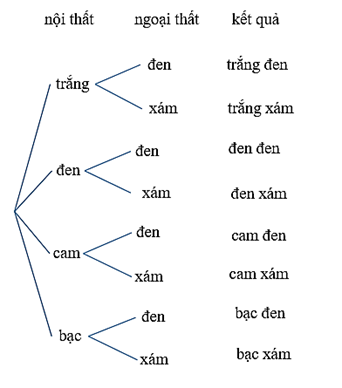
Thực hành 2 trang 24 Toán lớp 10 Tập 2:

Một mẫu xe ô tô có 4 màu ngoại thất là trắng, đen, cam và bạc. Mẫu xe này cũng có 2 màu nội thất là đen và xám

a) Khách hàng có bao nhiêu lựa chọn về màu ngoại thất và nội thất khi mua một chiếc xe ô tô mẫu này?

b) Hãy vẽ sơ đồ hình cây để giải thích cho kết quả tính toán trên.

Lời giải:

a) Việc lựa chọn về màu ngoại thất và nội thất khi mua một chiếc xe ô tô gồm 2 công đoạn:

Công đoạn thứ nhất: Chọn màu ngoại thất, có 4 cách lựa chọn màu

Công đoạn thứ 2: Ứng màu ngoại thất được chọn, có 2 cách lựa chọn màu nội thất.

Theo quy tắc nhân, ta có 4.2 = 8 cách lựa chọn ngoại thất và nội thất cho chiếc xe.

Vậy khách hàng có 8 lựa chọn về màu ngoại thất và nội thất khi mua một chiếc xe ô tô mẫu này

b) Sơ đồ cây:

Thực hành 3 trang 24 Toán lớp 10 Tập 2:

Có nhiều nhất bao nhiêu đoạn phân tử RNA khác nhau chứa 4 phân tử nucleotide, trong đó:

a) Không có nucleotide A nào?

b) Có nucleotide A nằm ở vị trí đầu tiên?

Lời giải:

a) Có thể coi việc tạo nên một đoạn phân tử RNA có 4 phân tử nucleotide là một công việc gồm 4 công đoạn ứng với việc chọn một trong ba loại nucleotide C, G hoặc U cho mỗi vị trí của đoạn. Như vậy mỗi công đoạn có 3 cách thực hiện.

Theo quy tắc nhân, 4 công đoạn có số cách thực hiện là:

3.3.3.3 = 3⁴ = 81

Vậy có nhiều nhất 81 đoạn phân tử RNA khác nhau chứa 4 phân tử nucleotide trong đó không có nucleotide A.

b) Có thể coi việc tạo nên một đoạn phân tử RNA có 4 phân tử nucleotide là một công việc gồm 4 công đoạn ứng với việc chọn một trong ba loại nucleotide A, C, G hoặc U cho mỗi vị trí của đoạn.

+ Công đoạn 1 : Chọn nucleotide cho vị trí thứ nhất là nuleotide A có: 1 cách chọn

+ Công đoạn 2; 3; 4 là chọn lần lượt nucleotide cho các vị trí 2, 3, 4 với mỗi công đoạn có 4 cách thực hiện.

Theo quy tắc nhân, 4 công đoạn có số cách thực hiện là:

4.4.4 = 4³ = 64

Vậy có nhiều nhất 64 đoạn phân tử RNA khác nhau chứa 4 phân tử nucleotide trong đó có nucleotide A nằm ở vị tri đầu tiên

Hoạt động Vận dụng trang 24 Toán lớp 10 Tập 2:

Trong phần khởi động đầu bài học này, nếu công ty có 2500 nhân viên thì số mã số như vậy có đủ để cấp cho mỗi nhân viên một mã số riêng hay không?

Lời giải:

Xem việc tạo mã số riêng cho từng nhân viên là một công việc gồm 3 công đoạn:

+ Công đoạn 1: Chọn 1 một chữ cái in hoa trong bảng chữ cái: có 26 cách chọn

+ Công đoạn 2: Ứng với việc chọn một chữ cái in hoa, thì công đoạn chọn chữ số đầu tiên lấy trong các chữ số từ 0 đến 9, có 10 cách chọn.

+ Công đoạn 3: Ứng với việc chọn một chữ cái in hoa và chữ số đầu tiên, thì công đoạn chọn chữ số cuối lấy trong các chữ số từ 0 đến 9, có 10 cách chọn.

Theo quy tắc nhân, số mã số riêng có thể tạo thành là: 26.10.10 = 2600 mã số

Nếu công ty có 2500 nhân viên nhỏ hơn 2600 mã số thẻ thì số mã số tạo thành có thể đủ cung cấp cho số nhân viên đó.

B. Bài tập

Bài 1 trang 24 Toán lớp 10 Tập 2:

Một thùng chứa 6 quả dưa hấu, một thùng khác chứa 15 quả thanh long. Từ hai thùng này:

a) Có bao nhiêu cách chọn một quả dưa hấu hoặc thanh long?

b) Có bao nhiêu cách chọn một quả dưa hấu và một quả thanh long?

Lời giải:

a) Việc chọn một loại quả từ hai thùng có 2 phương án để thực hiện:

Phương án 1: Chọn 1 quả dưa hấu, có 6 cách chọn.

Phương án 2: Chọn 1 quả thanh long, có 15 cách chọn.

Áp dụng quy tắc cộng, ta có số cách chọn một quả dưa hấu hoặc thanh long từ hai thùng là:

6 + 15 = 21 (cách).

Vậy có 21 cách chọn một quả dưa hấu hoặc một quả thanh long từ 2 thùng quả.

b) Việc chọn một quả thanh long hoặc một quả dưa hấu từ hai thùng là một công việc gồm hai công đoạn:

+ Công đoạn 1: Chọn một quả dưa hấu có 6 cách chọn

+ Công đoạn 2: Chọn một quả thanh long có 15 cách chọn

Áp dụng quy tắc nhân, ta có số cách chọn một quả dưa hấu và một quả thanh long là :

6 . 15 = 90 (cách chọn).

Vậy có 90 cách chọn một quả dưa hấu và một quả thanh long từ 2 thùng quả.

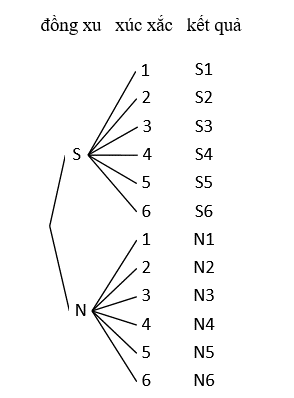
Bài 2 trang 24 Toán lớp 10 Tập 2:

Tung đồng thời một đồng xu và một con xúc xắc, nhận được kết quả là mặt xuất hiện trên đồng xu (sấp hay ngửa) và số chấm xuất hiện trên con xúc xắc.

a) Tính kết quả có thể xảy ra.

b) Vẽ sơ đồ hình cây và liệt kê tất cả các kết quả đó.

Lời giải:

a) Có thể xem việc tung đồng thời một đồng xu và một con xúc xắc là một công việc gồm 2 công đoạn:

+ Công đoạn 1: Tung đồng xu có 2 kết quả có thể xảy ra là S hoặc N

+ Công đoạn 2: Ứng với kết quả của đồng xu, tung xúc xắc có 6 kết quả có thể xảy ra số chấm là các số từ 1 đến 6.

Áp dụng quy tắc nhân, ta có các kết quả có thể xảy ra là: 2.6 = 12.

Vậy có 12 kết quả có thể xảy ra khi tung đồng thời một đồng xu và một con xúc xắc

b) Sơ đồ cây:

Giải Toán 10 trang 25 Tập 2

Bài 3 trang 25 Toán lớp 10 Tập 2:

Tại một nhà hàng chuyên phục vụ cơm trưa văn phòng, thực đơn có 5 món chính, 3 món phụ và 4 loại đồ uống. Tại đây, thực khách có bao nhiêu cách chọn bữa trưa gồm một món chính, một món phụ và một loại đồ uống?

Lời giải:

Việc thực khách lựa chọn bữa trưa gồm một món chính, một món phụ và một loại đồ uống là một công việc gồm 3 công đoạn:

+ Công đoạn 1: chọn 1 món chính: có 5 cách chọn.

+ Công đoạn 2: Ứng với món chính được chọn, chọn 1 món phụ: có 3 cách chọn.

+ Công đoạn 3: Ứng với món chính và món phụ, chọn 1 loại đồ uống: có 4 cách chọn.

Áp dụng quy tắc nhân, thực khách có số khách để chọn bữa trưa gồm:

5.3.4 = 60 (cách)

Vậy thực khách có 60 cách để chọn bữa trưa gồm một món chính, một món phụ và một loại đồ uống

Bài 4 trang 25 Toán lớp 10 Tập 2:

Có bao nhiêu số tự nhiên có ba chữ số, trong đó chữ số hàng trăm là chữ số chẵn, chữ số hàng đơn vị là chữ số lẻ

Lời giải:

Kí hiệu số có 3 chữ số cần tìm là: $\overline{abc}$

Có 4 cách lựa chọn chữ số a từ các chữ số chẵn khác 0 có 1 chữ số là 2, 4, 6, 8.

Ứng với mỗi cách chọn đó có 10 cách chọn chữ số b từ các số có 1 chữ số

Ứng với mỗi cách chọn đó có 5 các chọn chữ số c từ 5 chữ số lẻ có 1 chữ số: 1, 3, 5, 7, 9

Vậy, áp dụng quy tắc nhân có: 4.10.5 = 200 số tự nhiên có ba chữ số thoả mãn chữ số hàng trăm là chữ số chẵn, chữ số hàng đơn vị là chữ số lẻ

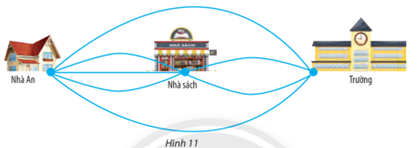
Bài 5 trang 38 Toán lớp 10 Tập 2:

An có thể đi từ nhà đến trường theo các con đường như hình 11, trong đó có những con đường đi qua nhà sách.

a) An có bao nhiêu cách đi từ nhà đến trường mà có đi qua nhà sách?

b) An có bao nhiêu cách đi từ nhà đến trường?

Lưu ý: Chỉ tính những đường đi qua các điểm (nhà An, nhà sách, trường) không quá một lần.

Lời giải:

a) Việc đi từ nhà qua nhà sách rồi đến trường gồm 2 công đoạn:

Công đoạn 1: Đi từ nhà đến nhà sách có 3 cách chọn đường đi.

Công đoạn 2: Đi từ nhà sách đến trường có 2 cách chọn đường đi.

Vậy theo quy tắc nhân có 3.2 = 6 cách chọn đường để đi từ nhà qua nhà sách rồi đến trường.

b) Việc An đi từ nhà đến trường có 2 phương án thực hiện:

Phương án 1: An đi từ nhà qua nhà sách rồi đến trường có 6 cách chọn đường.

Phương án 2 : An đi thẳng từ nhà đến trường có 2 cách chọn đường.

Vậy theo quy tắc cộng có 6 + 2 = 8 cách chọn đường để đi từ nhà đến trường.

Lý thuyết Quy tắc cộng và quy tắc nhân

1. Quy tắc cộng

– Giả sử một công việc có thể được thực hiện theo phương án A hoặc B. Phương án A có m cách thực hiện, phương án B có n cách thực hiện không trùng với bất kì cách nào của phương án A. Khi đó, công việc có thể thực hiện theo m + n cách.

Ví dụ: Lớp 10A có 20 học sinh, lớp 10C có 24 học sinh. Có bao nhiêu cách cử 1 học sinh lớp 10A hoặc lớp 10C đi tham dự đại hội Đoàn trường?

Hướng dẫn giải

Công việc cử 1 học sinh đi có 2 phương án thực hiện:

Phương án 1: Cử 1 học sinh của lớp 10A, ta có 20 cách.

Phương án 2: Cử 1 học sinh của lớp 10C, ta có 24 cách.

Ta thấy mỗi cách thực hiện của phương án B đều không trùng với cách của phương án A. Do đó theo quy tắc cộng, có 20 + 24 = 44 cách cử 1 học sinh lớp 10A hoặc lớp 10C đi tham dự đại hội Đoàn trường.

2. Quy tắc nhân

– Giả sử một công việc được chia thành hai công đoạn. Công đoạn thứ nhất có m cách thực hiện và ứng với mỗi cách đó có n cách thực hiện công đoạn thứ hai. Khi đó công việc có thể thực hiện theo m. n cách.

Ví dụ: Từ nhà An đến trường đi qua 3 điểm A, B, C. Từ nhà An đến điểm A có 3 cách đi, từ điểm A đến điểm B có 4 cách đi, từ điểm B đến điểm C có 2 cách đi. Từ điểm C đến trường học có 2 cách đi. Hỏi có bao nhiêu cách từ nhà An đến trường?

Hướng dẫn giải

Từ nhà An đến trường đi qua 3 điểm A, B, C, như vậy có 4 công đoạn:

+ Công đoạn 1: Từ nhà An đến điểm A có 3 cách đi.

+ Công đoạn 2: Từ điểm A đến điểm B có 4 cách đi

+ Công đoạn 3: Từ điểm B đến điểm C có 2 cách đi.

+ Công đoạn 4: Từ điểm C đến trường học có 2 cách đi.

Do đó, theo quy tắc nhân, có 3. 4. 2. 2 = 48 cách đi từ nhà An đến trường.

Xem thêm lời giải bài tập Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:

Bài 2: Hoán vị, chỉnh hợp và tổ hợp

Bài 3: Nhị thức Newton

Bài tập cuối chương 8

Bài 1: Tọa độ của vectơ

Bài 2: Đường thẳng trong mặt phẳng tọa độ