Giải Toán 10 Bài 3 (Chân trời sáng tạo): Đường tròn trong mặt phẳng tọa độ

Giải bài tập Toán 10 Bài 3: Đường tròn trong mặt phẳng tọa độ

Giải Toán 10 trang 59 Tập 2

Hoạt động khởi động trang 59 Toán lớp 10 Tập 2:

Một nông trại tưới nước theo phương pháp vòi phun xoay vòng trung tâm. Cho biết tâm một vòi phun được đặt tại tọa độ (30; 40) và vòi có thể phun xa tối đa 50 m. Làm thế nào để viết phương trình biểu diễn tập hợp các điểm xa nhất mà vòi này có thể phun tới?

Lời giải:

Phương trình biểu diễn tập hợp các điểm xa nhất mà vòi có thể phun tới là phương trình đường tròn tâm I(30; 40), bán kính R = 50 là: (x − 30)² + (y − 40)² = 50².

Hoạt động khám phá 1 trang 59 Toán lớp 10 Tập 2: Hãy nhắc lại công thức tính khoảng cách giữa hai điểm I(a; b) và M(x; y) trong mặt phẳng Oxy.

Lời giải:

Ta có: $\overrightarrow{IM}$ = (x – a; y – b)

Khi đó IM = $\left|\overrightarrow{IM}\right|$ = $\sqrt{{(x-a)}^2+{(y-b)}^2}$ .

Vậy khoảng cách giữa hai điểm I(a; b) và M(x; y) trong mặt phẳng Oxy là IM = $\sqrt{{(x-a)}^2+{(y-b)}^2}$ .

Giải Toán 10 trang 60 Tập 2

Thực hành 1 trang 60 Toán lớp 10 Tập 2: Viết phương trình đường tròn (C) trong các trường hợp sau:

a) (C) có tâm O(0; 0), bán kính R = 4;

b) (C) có tâm I(2; − 2), bán kính R = 8;

c) (C) đi qua ba điểm A(1; 4), B(0; 1), C(4; 3).

Lời giải:

a) Phương trình đường tròn (C) có tâm O(0; 0), bán kính R = 4 là: (x – 0)² + (y – 0)² = 4² hay x² + y² = 16.

Vậy phương trình đường tròn (C) có tâm O(0; 0), bán kính R = 4 là: x² + y² = 16.

b) Phương trình đường tròn (C) có tâm I(2; − 2), bán kính R = 8 là: (x − 2)² + (y + 2)² = 8² hay (x − 2)² + (y + 2)² = 64.

Vậy phương trình đường tròn (C) có tâm I(2; − 2), bán kính R = 8 là: (x − 2)² + (y + 2)² = 64.

c) Gọi I(a; b) là tâm đường tròn (C). Phương trình đường tròn (C) có dạng:

x² + y² − 2ax − 2by + c = 0 (a² + b² – c > 0).

Vì (C) đi qua ba điểm A(1; 4), B(0; 1), C(4; 3) nên ta có hệ phương trình:

$\left\{\begin{array}{l}{1}^2+4^2-2a-8b+c=0\\ 0^2+1^2-2b+c=0\\ 4^2+3^2-8a-6b+c=0\end{array}\right.$ ⇔ $\left\{\begin{array}{l}-2a-8b+c=-17\\ -2b+c=-1\\ -8a-6b+c=-25\end{array}\right.$ ⇔ $\left\{\begin{array}{l}a=2\\ b=2\\ c=3\end{array}\right.$

Vậy phương trình đường tròn (C) đi qua ba điểm A(1; 4), B(0; 1), C(4; 3) là: x² + y² − 4x − 4y + 3 = 0.

Giải Toán 10 trang 61 Tập 2

Thực hành 2 trang 61 Toán lớp 10 Tập 2: Phương trình nào sau đây là phương trình đường tròn? Tìm tọa độ tâm và bán kính của đường tròn đó.

a) x² + y² − 2x − 4y – 20 = 0;

b) (x + 5)² + (y + 1)² = 121;

c) x² + y² − 4x − 8y + 5 = 0;

d) 2x² + 2y² + 6x + 8y – 2 = 0.

Lời giải:

a) Phương trình đã cho có dạng: x² + y² − 2ax − 2by + c = 0 với a = 1; b = 2; c = −20.

Ta có: a² + b² − c = 1² + 2² + 20 = 25 > 0.

Vậy đây là phương trình đường tròn có tâm I(1; 2) và bán kính R = $\sqrt{25}$ = 5.

b) Phương trình có dạng (x − a)² + (y − b)² = R² với a = −5; b = −1; R = 11.

Vậy đây là phương trình đường tròn có tâm I(−5; −1) và bán kính R = 11.

c) Phương trình có dạng x² + y² − 2ax − 2by + c = 0 với a = 2; b = 4; c = 5.

Ta có: a² + b² − c = 2² + 4² – 5 = 15 > 0.

Vậy đây là phương trình đường tròn có tâm I(2; 4) và bán kính R = $\sqrt{15}$ .

d) Ta có: 2x² + 2y² + 6x + 8y – 2 = 0 ⇔ x² + y² + 3x + 4y – 1 = 0.

Phương trình có dạng x² + y² − 2ax − 2by + c = 0 với a = $-\frac{3}{2}$ ; b = −2; c = −1.

Ta có: a² + b² − c = ${\left(-\frac{3}{2}\right)}^2$ + (−2)² + 1 = $\frac{29}{4}$ > 0.

Vậy đây là phương trình đường tròn có tâm $I\left(-\frac{3}{2};-2\right)$ và bán kính R = $\frac{\sqrt{29}}{2}$ .

Vận dụng 1 trang 61 Toán lớp 10 Tập 2: Theo dữ kiện đã cho trong hoạt động khởi động của bài học, viết phương trình đường tròn biểu diễn tập hợp các điểm xa nhất mà vòi nước có thể phun tới.

Lời giải:

Phương trình biểu diễn tập hợp các điểm xa nhất mà vòi có thể phun tới là phương trình đường tròn tâm I(30; 40), bán kính R = 50 là: (x − 30)² + (y − 40)² = 50² hay (x − 30)² + (y − 40)² = 2 500

Vậy phương trình biểu diễn tập hợp các điểm xa nhất mà vòi có thể phun tới là (x − 30)² + (y − 40)² = 2 500.

Vận dụng 2 trang 61 Toán lớp 10 Tập 2: Một sân khấu đã được thiết lập một hệ trục tọa độ để đạo diễn có thể sắp đặt ánh sáng và xác định vị trí của các diễn viên. Cho biết một đèn chiếu sáng đang rọi trên sân khấu một vùng sáng bên trong đường tròn (C) có phương trình (x – 13)² + (y − 4)² = 16.

a) Tìm tọa độ tâm và bán kính của đường tròn (C).

b) Cho biết tọa độ trên sân khấu của ba diễn viên như sau: A(11; 4), B(8; 5), C(15; 5). Diễn viên nào đang được đèn chiếu sáng?

Lời giải:

a) Đường tròn (C): (x – 13)² + (y − 4)² = 16 có tâm I(13; 4) và bán kính R = $\sqrt{16}$ = 4.

Vậy đường tròn (C) có tâm I(13; 4) và bán kính R = $\sqrt{16}$ = 4.

b) Thay tọa độ điểm A(11; 4) vào phương trình đường tròn (C), ta được:

(11 − 13)² + (4 − 4)² = 4 < 16

⇒ Diễn viên A đứng trong vùng sáng bên trong đường tròn (C).

Do vậy diễn viên A đang được đèn chiếu sáng.

Thay tọa độ điểm B(8; 5) vào phương trình đường tròn (C), ta được:

(8 − 13)² + (5 − 4)² = 26 >16

⇒ Diễn viên B đứng ngoài vùng sáng bên trong đường tròn (C).

⇒ Diễn viên B không được chiếu sáng.

Thay tọa độ điểm C(15; 5) vào phương trình đường tròn (C), ta được:

(15 − 13)² + (5 − 4)² = 5 < 16 ⇒ Diễn viên C đứng trong vùng sáng bên trong đường tròn (C).

⇒ Diễn viên C đang được chiếu sáng.

Vậy diễn viên A và C đang được đèn chiếu sáng, diễn viên B không được chiếu sáng.

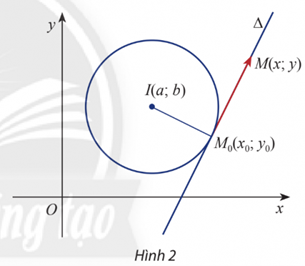
Hoạt động khám phá 2 trang 61 Toán lớp 10 Tập 2: Cho điểm M₀(x₀;y₀) nằm trên đường tròn (C) tâm I(a; b) và cho điểm M(x; y) tùy ý trong mặt phẳng Oxy. Gọi Δ là tiếp tuyến với (C) tại M₀.

a) Viết tọa độ của hai vectơ $\overrightarrow{M_{0}M}$ và $\overrightarrow{M_{0}I}$ .

b) Viết biểu thức tọa độ tích vô hướng của hai vectơ $\overrightarrow{M_{0}M}$ và $\overrightarrow{M_{0}I}$.

c) Phương trình $\overrightarrow{M_{0}M}$ . $\overrightarrow{M_{0}I}$ = 0 là phương trình của đường thẳng nào?

Lời giải:

a) Ta có : $\overrightarrow{M_{0}M}$ = (x – x₀; y – y₀); $\overrightarrow{M_{0}I}$ = (a – x₀; b – y₀)

b) Ta có: $\overrightarrow{M_{0}M}$ . $\overrightarrow{M_{0}I}$ = (x – x₀).(a – x₀) + (y – y₀).(b – y₀)

c) Phương trình $\overrightarrow{M_{0}M}$ . $\overrightarrow{M_{0}I}$ = 0 tức là

(x – x₀).(a – x₀) + (y – y₀).(b – y₀) = 0 ⇔ (a – x₀).(x – x₀) + (b – y₀).(y – y₀) = 0 (1)

Mặt khác:

Vì Δ là tiếp tuyến với (C) tại M₀ nên M₀I ⊥ Δ

⇒ Đường thẳng Δ nhận $\overrightarrow{M_{0}I}$ = (a – x₀; b – y₀) làm vectơ pháp tuyến.

Khi đó, đường thẳng Δ đi qua điểm M₀(x₀;y₀) có vectơ pháp tuyến $\overrightarrow{M_{0}I}$ = (a – x₀; b – y₀) có phương trình là: (a – x₀).(x – x₀) + (b – y₀).(y – y₀) = 0 (2)

Từ (1) và (2) suy ra $\overrightarrow{M_{0}M}$ . $\overrightarrow{M_{0}I}$ = 0 là phương trình đường thẳng Δ.

Vậy phương trình $\overrightarrow{M_{0}M}$ . $\overrightarrow{M_{0}I}$ = 0 là phương trình của đường thẳng Δ.

Giải Toán 10 trang 62 Tập 2

Thực hành 3 trang 62 Toán lớp 10 Tập 2: Viết phương trình tiếp tuyến của đường tròn (C): x² + y² − 2x − 4y − 20 = 0 tại điểm A(4; 6).

Lời giải:

Phương trình đường tròn (C): x² + y² − 2x − 4y − 20 = 0 có dạng: x² + y² − 2ax − 2by + c = 0 với a = 1; b = 2; c = −20.

Ta có: a² + b² − c = 1² + 2² + 20 = 25.

⇒ Đường tròn (C) có tâm I(1; 2) và bán kính R = $\sqrt{25}$ = 5.

Phương trình tiếp tuyến của (C) tại A(4; 6) là:

(1 − 4)(x − 4) + (2 − 6)(y − 6) = 0 ⇔ −3x − 4y + 36 = 0 ⇔ 3x + 4y – 36 = 0.

Vậy phương trình tiếp tuyến của đường tròn (C): x² + y² − 2x − 4y − 20 = 0 tại điểm A(4; 6) là 3x + 4y – 36 = 0.

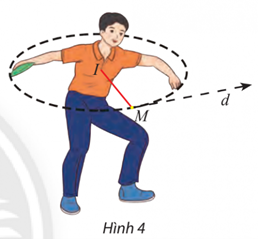
Vận dụng 3 trang 62 Toán lớp 10 Tập 2: Một vận động viên ném đĩa đã vung đĩa theo một đường tròn (C) có phương trình: (x − 1)² + (y − 1)² = $\frac{169}{144}$ .

Khi người đó vung đĩa đến vị trí điểm $M\left(\frac{17}{12};2\right)$ thì buông đĩa (Hình 4). Viết phương trình tiếp tuyến của đường tròn (C) tại điểm M.

Lời giải:

Đường tròn (C): (x − 1)² + (y − 1)² = $\frac{169}{144}$ có tâm I(1; 1).

Phương trình tiếp tuyến của đường tròn (C) tại điểm M là:

(1 − $\frac{17}{12}$ )(x − $\frac{17}{12}$ ) + (1 − 2)(y − 2) = 0 ⇔ $\frac{5}{12}$x + y − $\frac{373}{144}$ = 0.

Vậy phương trình tiếp tuyến của đường tròn (C) tại điểm M là $\frac{5}{12}$ x + y − $\frac{373}{144}$ = 0.

Bài tập 1 trang 62 Toán lớp 10 Tập 2: Phương trình nào trong các phương trình sau đây là phương trình đường tròn? Tìm tọa độ tâm và bán kính của đường tròn đó.

a) x² + y² − 6x − 8y + 21 = 0;

b) x² + y² − 2x + 4y + 2 = 0;

c) x² + y² − 3x + 2y + 7 = 0;

d) 2x² + 2y² + x + y – 1 = 0.

Lời giải:

a) Phương trình có dạng x² + y² − 2ax − 2by + c = 0 với a = 3, b = 4, c = 21

Ta có: a² + b² − c = 3² + 4² – 21 = 4 > 0.

Vậy đây là phương trình đường tròn có tâm I(3; 4) và có bán kính R = $\sqrt{4}$ = 2.

b) Phương trình có dạng x² + y² − 2ax − 2by + c = 0 với a = 1, b = −2, c = 2.

Ta có: a² + b² − c = 1² + (−2)² – 2 = 3 > 0.

Vậy đây là phương trình đường tròn có tâm I(1; −2) và có bán kính R = $\sqrt{3}$ .

c) Phương trình có dạng x² + y² − 2ax − 2by + c = 0 với a = $\frac{3}{2}$ , b = −1, c = 7.

Ta có: a² + b² − c = ${\left(\frac{3}{2}\right)}^2$ + (−1)² −7 = −3,75 < 0.

Vậy đây không phải là phương trình đường tròn.

d) Ta có: 2x² + 2y² + x + y – 1 = 0 ⇔ x² + y² + $\frac{1}{2}$ x + $\frac{1}{2}$ y − $\frac{1}{2}$ = 0.

Phương trình có dạng x² + y² − 2ax − 2by + c = 0 với a = $-\frac{1}{4}$ , b = $-\frac{1}{4}$ , c = $-\frac{1}{2}$

Ta có: a² + b² − c = ${\left(-\frac{1}{4}\right)}^2$ + ${\left(-\frac{1}{4}\right)}^2$ + $\frac{1}{2}$ = $\frac{5}{8}$ > 0.

Vậy đây là phương trình đường tròn có tâm $I\left(-\frac{1}{4};-\frac{1}{4}\right)$ và bán kính R = $\frac{\sqrt{10}}{4}$ .

Bài tập 2 trang 62 Toán lớp 10 Tập 2: Lập phương trình đường tròn (C) trong các trường hợp sau:

a) (C) có tâm I(1; 5) và có bán kính r = 4;

b) (C) có đường kính MN với M(3; −1) và N(9; 3);

c) (C) có tâm I(2; 1) và tiếp xúc với đường thẳng 5x − 12y + 11= 0;

d) (C) có tâm A(1; −2) và đi qua điểm B(4; −5).

Lời giải:

a) Phương trình đường tròn (C) tâm I(1; 5) và bán kính r = 4 là: (x − 1)² + (y − 5)² = 16.

b) Tâm I của đường tròn (C) là trung điểm của MN ⇒ $I\left(\frac{3+9}{2};\frac{-1+3}{2}\right)$ ⇒ I(6; 1)

Ta có: $\overrightarrow{MI}$ = (6−3; 1+1) = (3; 2)

R = MI = $\left|\overrightarrow{MI}\right|$ = $\sqrt{3^2+2^2}$ = $\sqrt{13}$ .

Phương trình đường tròn (C) tâm I(6; 1) và bán kính R = $\sqrt{13}$ là: (x − 6)² + (y − 1)² = 13.

c) Gọi ∆ là đường thẳng 5x − 12y + 11= 0.

Vì (C) tiếp xúc với đường thẳng ∆: 5x − 12y + 11 = 0 nên bán kính R = d(I, ∆)

d(I, ∆) = $\frac{|5.2-12.1+11|}{\sqrt{5^2+{(-12)}^2}}$ = $\frac{9}{13}$ .

⇒ R = d(I, ∆) = $\frac{9}{13}$ .

Phương tròn đường tròn (C) tâm I(2; 1) và bán kính R = $\frac{9}{13}$ là: (x − 2)² + (y − 1)² = $\frac{81}{169}$

d) Ta có $\overrightarrow{AB}$ = (4−1; −5+2) = (3; −3) ⇒ AB = $\left|\overrightarrow{AB}\right|$ = $\sqrt{3^2+{(-3)}^2}$ = $3\sqrt{2}$ .

Vì (C) có tâm A(1; −2) và đi qua điểm B(4; −5) nên bán kính R = AB = $3\sqrt{2}$.

Vậy phương trình đường tròn (C) tâm A(1; −2) và bán kính R = $3\sqrt{2}$ là: (x − 1)² + (y + 2)² = 18.

Bài tập 3 trang 62 Toán lớp 10 Tập 2: Lập phương trình đường tròn ngoại tiếp tam giác có tọa độ các đỉnh là:

a) M(2; 5), N(1; 2), P(5; 4);

b) A(0; 6), B(7; 7), C(8; 0).

Lời giải:

a) Phương trình đường tròn có dạng x² + y² − 2ax − 2by + c = 0.

Thay tọa độ các đỉnh M(2; 5), N(1; 2), P(5, 4) vào phương trình đường tròn, ta được hệ phương trình: $\left\{\begin{array}{c}{2}^2+5^2-4a-10b+c=0\\ 1^2+2^2-2a-4b+c=0\\ 5^2+4^2-10a-8b+c=0\end{array}\right.$ ⇔ $\left\{\begin{array}{c}-4a-10b+c=-29\\ -2a-4b+c=-5\\ -10a-8b+c=-41\end{array}\right.$ ⇔ $\left\{\begin{array}{c}a=3\\ b=3\\ c=13\end{array}\right.$

Vậy phương trình đường tròn ngoại tiếp tam giác MNP là: x² + y² − 6x − 6y + 13 = 0.

b) Phương trình đường tròn có dạng x² + y² − 2ax − 2by + c = 0.

Thay tọa độ các đỉnh A(0; 6), B(7; 7), C(8; 0) vào phương trình đường tròn, ta được hệ phương trình: $\left\{\begin{array}{c}{6}^2-12b+c=0\\ 7^2+7^2-14a-14b+c=0\\ 8^2-16a+c=0\end{array}\right.$ ⇔ $\left\{\begin{array}{c}-12b+c=-36\\ -14a-14b+c=-98\\ -16a+c=-64\end{array}\right.$ ⇔ $\left\{\begin{array}{c}a=4\\ b=3\\ c=0\end{array}\right.$

Vậy phương trình đường tròn ngoại tiếp tam giác ABC là: x² + y² − 8x − 6y = 0.

Bài tập 4 trang 62 Toán lớp 10 Tập 2: Lập phương trình đường tròn tiếp xúc với hai trục Ox, Oy và đi qua điểm A(4; 2).

Lời giải:

Gọi I(a; b) là tâm đường tròn (C).

Ta có: R = d(I; Ox) = d(I; Oy) ⇒ R = a = b ⇒ (C) có tâm I(a; a) và bán kính R = a.

⇒ Phương trình đường tròn (C) là: (x − a)² + (y − a)² = a².

Ta có A(4; 2) ∈ (C) nên (4 − a)² + (2 − a)² = a²

⇔ 16 − 8a + a² + 4 − 4a + a² = a²

⇔ a² − 12a + 20 = 0 ⇔ a = 10 hoặc a = 2

Với a = 10 thì ta có phương trình đường tròn (C): (x − 10)² + (y − 10)² = 100.

Với a = 2 thì ta có phương trình đường tròn (C): (x − 2)² + (y − 2)² = 4.

Vậy (C): (x − 10)² + (y − 10)² = 100 hoặc (C): (x − 2)² + (y − 2)² = 4.

Giải Toán 10 trang 63 Tập 2

Bài tập 5 trang 63 Toán lớp 10 Tập 2: Cho đường tròn (C) có phương trình x² + y² − 2x − 4y – 20 = 0.

a) Chứng tỏ rằng điểm M(4; 6) thuộc đường tròn (C).

b) Viết phương trình tiếp tuyến của (C) tại điểm M(4; 6).

c) Viết phương trình tiếp tuyến của (C) song song với đường thẳng 4x + 3y + 2022 = 0.

Lời giải:

a) Thay tọa độ điểm M vào phương trình đường tròn (C), ta có:

4² + 6² − 2.4 − 4.6 – 20 = 0

⇒ M ∈ (C).

Vậy điểm M(4; 6) thuộc đường tròn (C).

b) Đường tròn (C) x² + y² − 2x − 4y – 20 = 0 có a = 1; b = 2; c = −20.

Khi đó R = $\sqrt{1^2+2^2+20}$ = 5 và tâm I(1; 2).

Phương trình tiếp tuyến của (C) tại M(4; 6) là:

(1 − 4)(x − 4) + (2 − 6)(y − 6) = 0 ⇔ −3x − 4y + 36 = 0 ⇔ 3x + 4y – 36 = 0.

Vậy phương trình tiếp tuyến của (C) tại điểm M(4; 6) là 3x + 4y – 36 = 0.

c) Tiếp tuyến Δ của (C) song song với đường thẳng 4x + 3y + 2022 = 0 có dạng

Δ: 4x + 3y + c = 0 (với c ≠ 2022)

Ta có: d(I; Δ) = R ⇔ $\frac{\left|4.1+3.2+c\right|}{\sqrt{4^2+3^2}}$ = 5 ⇔ $\frac{\left|10+c\right|}{5}$ = 5 ⇔ |10 + c| = 25 ⇔ c = 15 hoặc c = −35.

Vậy phương trình tiếp tuyến của (C) song song với đường thẳng 4x + 3y + 2022 = 0 là: Δ: 4x + 3y + 15 = 0 hoặc Δ: 4x + 3y – 35 = 0.

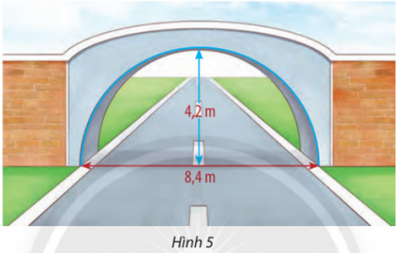
Bài tập 6. trang 63 Toán lớp 10 Tập 2: Một cái cổng hình bán nguyệt rộng 8,4m, cao 4,2m như Hình 5. Mặt đường dưới cổng được chia thành hai làn xe ra vào.

a) Viết phương trình mô phỏng cái cổng.

b) Một chiếc xe tải rộng 2,2 m và cao 2,6m đi đúng làn đường quy định có thể đi qua cổng mà không làm hư hỏng cổng hay không?

Lời giải:

a) Chọn hệ tọa độ Oxy như hình vẽ.

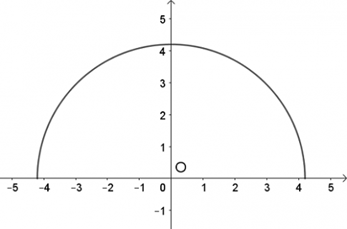
Ta có phương trình đường tròn tâm O(0; 0) bán kính R = 8,4 : 2 = 4,2 là:

x² + y² = 17,64.

Vậy phương trình mô phỏng cái cổng là: x² + y² = 17,64 (y ≥ 0)

b) Chiếc xe tải rộng 2,2 m và cao 2,6m tương ứng với x = 2,2 và chiều cao của cổng tại x = 2,2 phải lớn hơn 2,6 thì xe tải mới đi qua được.

Thay x = 2,2 vào phương trình đường tròn, ta được 2,2² + y² = 17,64

⇒ y² = 17,64 – 2,2² = 12,8

Vì y > 0 nên y = $\sqrt{\mathrm{12,8}}$ ≈ 3,6 > 2,6.

Vậy xe tải rộng 2,2m và cao 2,6m đi đúng làn đường quy định có thể đi qua cổng mà không làm hư hỏng cổng.

Lý thuyết Toán 10 Bài 3. Đường tròn trong mặt phẳng tọa độ - Chân trời sáng tạo

1. Phương trình đường tròn

Trong mặt phẳng Oxy, cho đường tròn (C) tâm I(a; b), bán kính R.

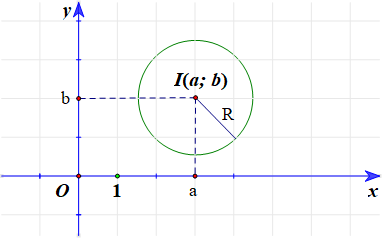Phương trình (x – a)² + (y – b)² = R² được gọi là phương trình đường tròn tâm I(a; b), bán kính R.

Ví dụ: Viết phương trình đường tròn (C) trong các trường hợp sau:

a) (C) có tâm I(2; –3), bán kính R = 2.

b) (C) có đường kính AB với A(1; 6), B(–3; 2).

c) (C) đi qua ba điểm A(–2; 4), B(5; 5), C(6; –2).

Hướng dẫn giải

a) Đường tròn (C) có tâm I(2; –3), bán kính R = 2.

Vậy phương trình đường tròn (C): (x – 2)² +(y + 3)² = 4.

b) Gọi I(a; b) là tâm của đường tròn (C).

Vì đường tròn (C) có tâm I(a; b) và đường kính AB nên I là trung điểm AB.

Với A(1; 6), B(–3; 2).

Suy ra $\left\{\begin{array}{l}a=\frac{x_A+x_B}{2}=\frac{1-3}{2}=-1\\ b=\frac{y_A+y_B}{2}=\frac{6+2}{2}=4\end{array}\right.$

Khi đó ta có tọa độ I(–1; 4).

Ta có $\overrightarrow{IA}=\left(2;2\right)$.

Suy ra $R=IA=\left|\overrightarrow{IA}\right|=\sqrt{2^2+2^2}=2\sqrt{2}$.

Đường tròn (C) có tâm I(–1; 4), bán kính $R=2\sqrt{2}$.

Vậy phương trình đường tròn (C): (x + 1)² + (y – 4)² = 8.

c) Gọi M, N lần lượt là trung điểm của AB, AC.

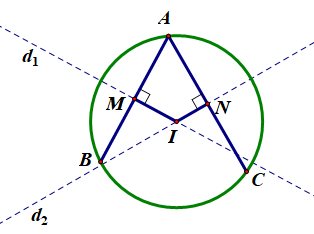
Ta có M là trung điểm AB với A(–2; 4), B(5; 5).

Suy ra $\left\{\begin{array}{l}{x}_M=\frac{x_A+x_B}{2}=\frac{-2+5}{2}=\frac{3}{2}\\ y_M=\frac{y_A+y_B}{2}=\frac{4+5}{2}=\frac{9}{2}\end{array}\right.$

Khi đó ta có $M\left(\frac{3}{2};\frac{9}{2}\right)$.

Tương tự, ta có N(2; 1).

Với A(–2; 4), B(5; 5), C(6; –2) ta có $\overrightarrow{AB}=\left(7;1\right),\overrightarrow{AC}=\left(8;-6\right)$.

Đường trung trực d₁ của đoạn thẳng AB đi qua điểm $M\left(\frac{3}{2};\frac{9}{2}\right)$, có vectơ pháp tuyến $\overrightarrow{AB}=\left(7;1\right)$.

Suy ra phương trình d₁: $7\left(x-\frac{3}{2}\right)+1\left(y-\frac{9}{2}\right)=0\iff 7x+y-15=0$.

Tương tự, ta có phương trình đường trung trực d₂ của đoạn thẳng AC:

8(x – 2) – 6(y – 1) = 0 ⇔ 4x – 3y – 5 = 0.

Vì đường tròn (C) có tâm I(a; b) và (C) đi qua ba điểm A, B, C nên IA = IB = IC (= R).

Vì IA = IB nên I nằm trên đường trung trực d₁ của đoạn thẳng AB.

Tương tự, ta có I nằm trên đường trung trực d₂ của đoạn thẳng AC.

Vì vậy ta suy ra I là giao điểm của d₁ và d₂.

Khi đó tọa độ điểm I là nghiệm của hệ phương trình:

$\left\{\begin{array}{l}7x+y-15=0\\ 4x-3y-5=0\end{array}\right.\iff \left\{\begin{array}{l}x=2\\ y=1\end{array}\right.$

Suy ra I(2; 1).

Với I(2; 1) và A(–2; 4) ta có $\overrightarrow{IA}=\left(-4;3\right)$.

Suy ra $R=IA=\left|\overrightarrow{IA}\right|=\sqrt{{\left(-4\right)}^2+3^2}=5$.

Vậy phương trình đường tròn (C): (x – 2)² + (y – 1)² = 25.

Ví dụ: Tìm tâm và bán kính của đường tròn (C) có phương trình trong mỗi trường hợp sau:

a) (x – 4)² + (y – 10)² = 9.

b) (x + 2)² + (y – 5)² = 64.

c) x² + (y – 1)² = 36.

Hướng dẫn giải

a) (x – 4)² + (y – 10)² = 9

Đường tròn (C) có tâm I(4; 10), bán kính $R=\sqrt{9}=3$.

b) (x + 2)² + (y – 5)² = 64

Đường tròn (C) có tâm I(–2; 5), bán kính $R=\sqrt{64}=8$.

c) x² + (y – 1)² = 36.

Đường tròn (C) có tâm I(0; 1), bán kính $R=\sqrt{36}=6$.

Nhận xét: Ta có (x – a)² + (y – b)² = R²

⇔ x² + y² – 2ax – 2by + (a² + b² – R²) = 0.

Vậy phương trình đường tròn (x – a)² + (y – b)² = R² có thể được viết dưới dạng x² + y² – 2ax – 2by + c = 0, trong đó c = a² + b² – R².

Ngược lại, phương trình x² + y² – 2ax – 2by + c = 0 là phương trình của đường tròn (C) khi và chỉ khi a² + b² – c > 0. Khi đó đường tròn (C) có tâm I(a; b) và bán kính $R=\sqrt{a^2+b^2-c}$.

Ví dụ: Phương trình nào trong các phương trình sau đây là phương trình đường tròn? Nếu là phương trình đường tròn, hãy tìm tọa độ tâm và bán kính của đường tròn đó.

a) x² + y² + 2x – 6y – 15 = 0.

b) 2x² + 2y² + 4x + 8y + 14 = 0.

Hướng dẫn giải

a) Phương trình đã cho có dạng: x² + y² – 2ax – 2by + c = 0, với a = –1, b = 3, c = –15.

Ta có a² + b² – c = 1 + 9 + 15 = 25 > 0.

Vậy phương trình đã cho là phương trình đường tròn có tâm I(–1; 3), bán kính R = 5.

b) Ta có 2x² + 2y² + 4x + 8y + 14 = 0 ⇔ x² + y² + 2x + 4y + 7 = 0.

Phương trình trên có dạng x² + y² – 2ax – 2by + c = 0, với a = –1, b = –2, c = 7.

Ta có a² + b² – c = 1 + 4 – 7 = –2 < 0.

Vậy phương trình đã cho không phải là phương trình đường tròn.

2. Phương trình tiếp tuyến của đường tròn

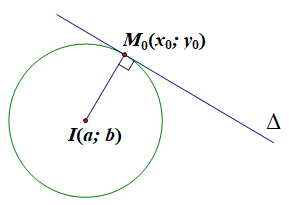
Phương trình tiếp tuyến của đường tròn tâm I(a; b) tại điểm M₀(x₀; y₀) nằm trên đường tròn là:

(a – x₀)(x – x₀) + (b – y₀)(y – y₀) = 0.

Ví dụ: Viết phương trình tiếp tuyến d của đường tròn (C): (x – 2)² + (y + 3)² = 5 tại điểm M(3; –1).

Hướng dẫn giải

Ta có (3 – 2)² + (–1 + 3)² = 5.

Suy ra M ∈ (C).

Đường tròn (C) có tâm I(2; –3).

Phương trình tiếp tuyến d của đường tròn (C) tại điểm M(3; –1) là:

(2 – 3)(x – 3) + [–3 – (–1)].[y – (–1)] = 0.

⇔ –1.(x – 3) + (–2).(y + 1) = 0.

⇔ –x – 2y + 1 = 0.

Vậy phương trình tiếp tuyến d của đường tròn (C) cần tìm là –x – 2y + 1 = 0.

Xem thêm lời giải bài tập Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:

Bài 4: Ba đường conic trong mặt phẳng tọa độ

Bài tập cuối chương 9

Bài 1: Không gian mẫu và biến cố

Bài 2: Xác suất của biến cố

Bài tập cuối chương 10